VANISHING VISCOSITY FOR NON-ISENTROPIC GAS DYNAMICS WITH INTERACTING SHOCKS∗
Xiaoding SHI(施小丁)
School of Science,Beijing University of Chemical Technology,Beijing 100029,China
Yan YONG(雍燕)
College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China
Yinglong ZHANG(张英龙)
Institute of Applied Mathematics,Academy of Mathematics and Systems Science, Chinese Academy of Sciences,Beijing 100190,China
VANISHING VISCOSITY FOR NON-ISENTROPIC GAS DYNAMICS WITH INTERACTING SHOCKS∗
Xiaoding SHI(施小丁)
School of Science,Beijing University of Chemical Technology,Beijing 100029,China
E-mail:shixd@mail.buct.edu.cn
Yan YONG(雍燕)
College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China
E-mail:yongyan@usst.edu.cn
Yinglong ZHANG(张英龙)
Institute of Applied Mathematics,Academy of Mathematics and Systems Science, Chinese Academy of Sciences,Beijing 100190,China
E-mail:yinglongzhang@amss.ac.cn
In this paper,we study the vanishing viscosity limit for non-isentropic gas dynamics with interacting shocks.Given any entropy solution of non-isentropic gas dynamics which consists of two diferent families of shocks interacting at some positive time,we show that such solution is the vanishing viscosity limit of a family of smooth global solutions for a viscous system of conservation law.We remark that,after the interacting time,not only shocks but also contact discontinuity are generated.
vanishing viscosity;non-isentropic gas dynamics;interacting shock;contact discontinuity
2010 MR Subject Classifcation35Q31;35B65
1 Introduction and Main Results
In this paper,we consider the vanishing viscosity limit of solutions to non-isentropic gas dynamics with artifcial viscosity

where v(x,t)>0 is the special volume,u(x,t)is the velocity,and θ>0 is the absolute temperature of the gas.The pressure p and the total energy E are given by the equations ofstate

where the constants R>0 and γ>1 denote the gas constant and the adiabatic exponent, respectively.
Formally,as ǫ→0+,system(1.1)tends to the following non-isentropic gas dynamics system

The vanishing viscosity limit of solutions to gas dynamics system was an open and challenging problem with a long history.When the solution of gas dynamics system is smooth,the problem can be studied by scaling method.However,it is known that its solution in general develops singularity in the fnite time such as shock waves.Thus it is interesting but difcult to study the vanishing viscosity in the case when the solution of gas dynamics system does not possess smooth solution.
Now let us give some related works on the vanishing viscosity limit of viscous fuid system. For general hyperbolic conservation laws with artifcial viscosity

Goodman and Xin[5]proved the vanishing viscosity limit for(1.3)in L∞norm for piecewise smooth solutions separated by non-interacting shocks.For the Navier-Stokes equations,i.e., the viscosity matrix is not positive defnite,Hof-Liu[6],Xin[25]proved the vanishing viscosity limit of single shock and rarefaction wave,respectively.We refer to[7–12,14–16,19,24,27,28] and reference therein for related works.For interacting shocks,Serre[21]showed the vanishing viscosity limit associated with general viscous conservation laws in L2norm.Bianchini-Bressan [1],Bressan-Huang-Wang-Yang[2]and Bressan-Yang[3]studied the vanishing viscosity limit in BV space.Huang-Wang-Wang-Yang[13]frst studied the vanishing viscosity limit for onedimensional isentropic compressible Navier-Stokes equations in the case of two diferent of families of interacting shocks in L∞norm which gives detailed information of vanishing viscosity limits.Precisely speaking,they studied the simplest case,where after the shocks interact,only shocks are generated.Moreover,they pointed out that it is interesting and meaningful to study the problem of the vanishing viscosity of non-isentropic system for the interacting shocks.Along this direction,we begin to study the vanishing viscosity problem for(1.1)with artifcial viscosity. It is noted even in the simplest case where the two shocks belong to two diferent of families,not only two outgoing shocks but also a contact discontinuity are generated after the two shocks hit.This makes the problem complicated.The vanishing viscosity limit for the non-isentropic Navier-Stokes equations is difcult and left for the future.
Now let us formulate our main result.Note that the eigenvalues of the non-isentropic gas dynamics system(1.2)are
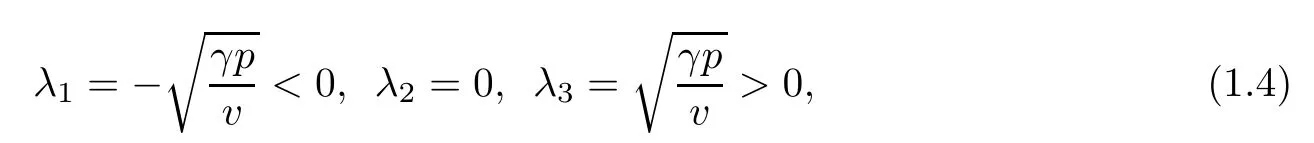
where the frst and the third characteristic felds are genuinely nonlinear and the second characteristic feld is linearly degenerate.
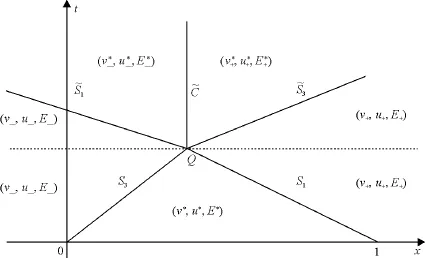
Figure 1 Entropy solution
Given two incoming shocks denoted by S1,S3,respectively,see Figure 1,where S1is the 1-shock which connects(v∗,u∗,E∗)as the left state and(v+,u+,E+)as the right state with the speed s1<0,while S3is the 3-shock which connects(v−,u−,E−)as the left state and (v∗,u∗,E∗)as the right state with the speed s3>0.Because the shock wave S3propagates faster than shock wave S1,the two shocks must interact at some point Q=(x0,t0)with t0>0. Diferent from[13],after interaction,two outgoing shockseS1,eS3and a contact discontinuity eC are generated.In this case,the intermediate state betweeneS1andeC is(v∗−,u∗−,E∗−),the intermediate state betweeneS3andeC is(v∗+,u∗+,E∗+),and these two intermediate states are determined by the R-H condition.Without loss of generality,we assume the initial data of the Euler system(1.2)is
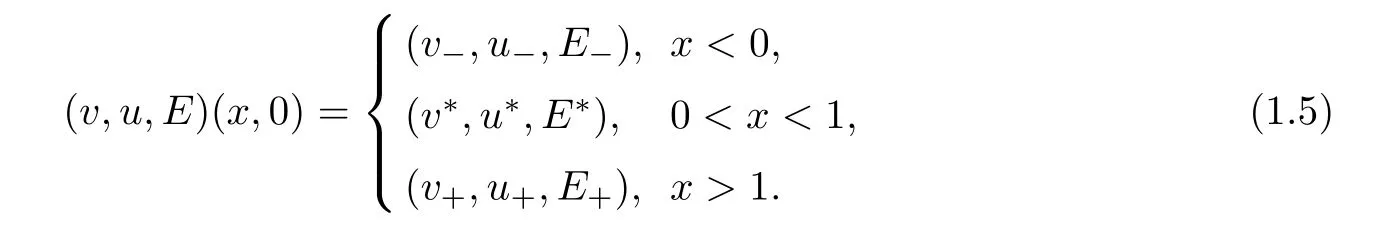
We denote the unique entropy solution of(1.2),(1.5)by(vS,uS,ES).It is obvious that before the interaction time,(vS,uS,ES)satisfes

By a simple calculation,the two incoming shocks hit at the pointwhere s1and s3are determined by the following R–H conditionsand the entropy conditions
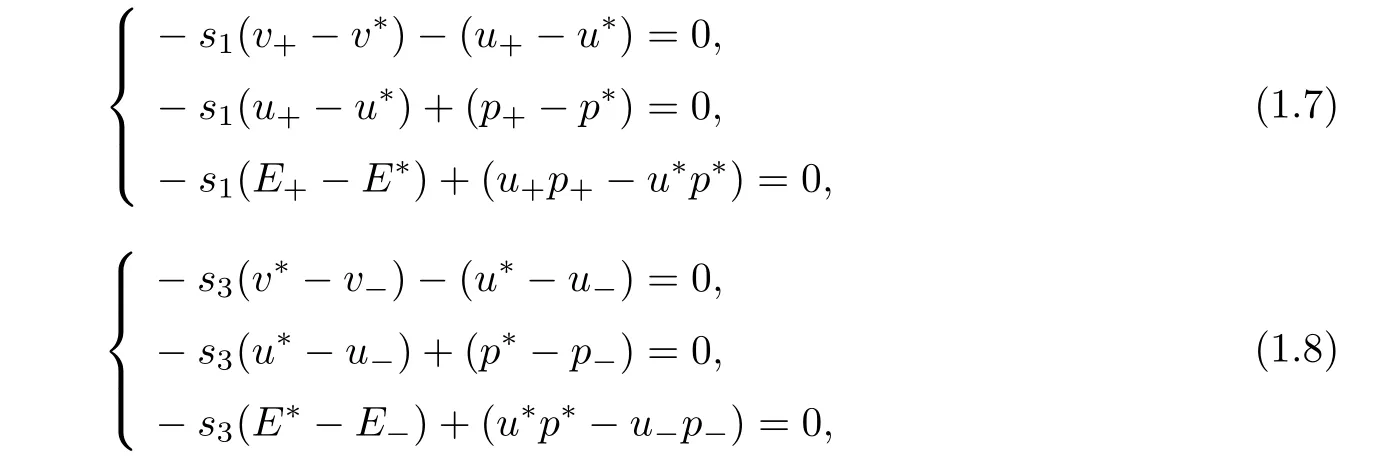

After the interacting time t0,it is equivalent to resolve the Riemann problem of system(1.2) with initial data at t=t0,
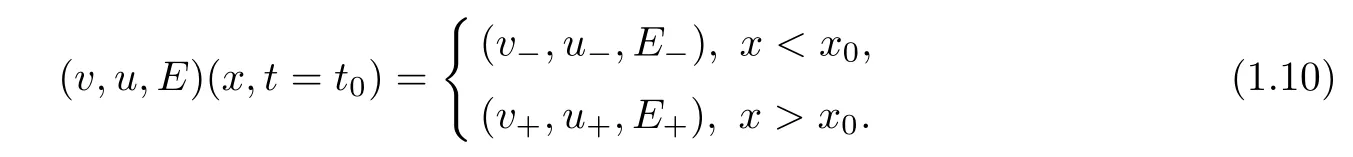
The formula of(vS,uS,ES)after the interaction time t=t0is
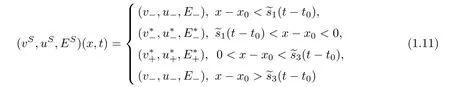
with t≥t0,the contact discontinuity speed e s2=0 and the shock speeds e si,i=1,3 satisfy the following R–H conditions
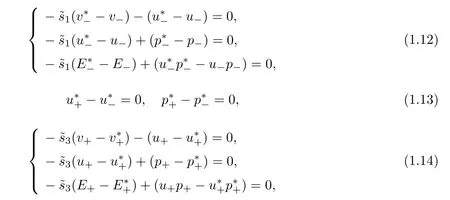
and the entropy conditions

We set
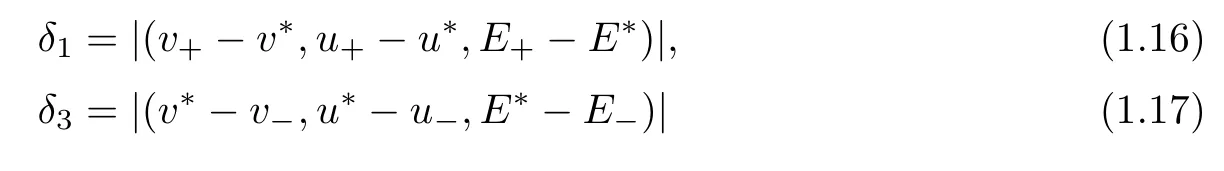
be the strengths of the two incoming shocks,and δ=min{δ1,δ3}.We call the strengths of shock waves“small with the same order”if the following condition holds
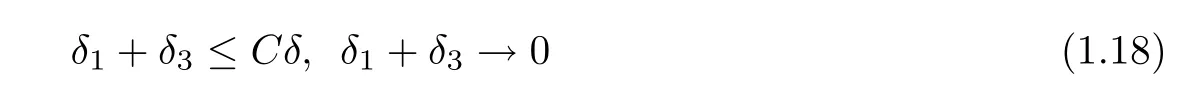
for a positive constant C.Through out the paper,we always assume(1.18)hold.On the other hand,we denote bythe wave strengths of the outgoing waves respectively.From[23],we know that
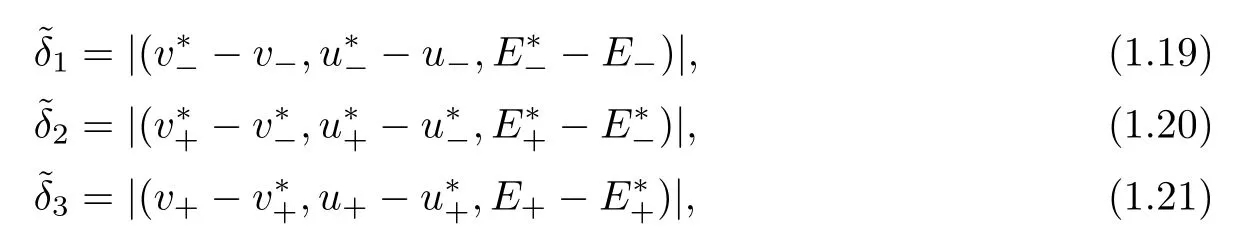

if δ is small,which gives the relations of the wave strengths between the incoming and the outgoing waves.The following theorem is the main result in this paper.
Theorem 1.1Assume(vS,uS,ES)is the entropy solution of system(1.2),(1.5)given by (1.6)and(1.11).Then there exists a positive constant δ0such that if the wave strength satisfes δ≤δ0,system(1.1)admits a family of global smooth solution(vǫ,uǫ,Eǫ)with well-prepared initial data(3.3)below.Moreover,before the interaction time t=t0,it holds that
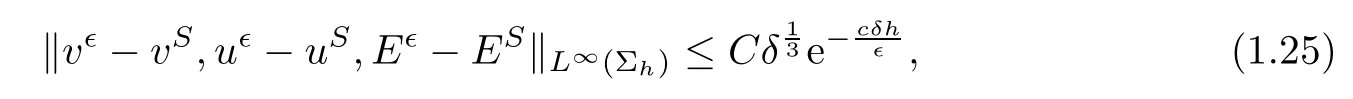
where Σh={(x,t)||x−s3t|≥h,|x−s1t−1|≥h,0≤t≤t0−h}for any positive constant h>0.After the interaction time t0,it holds that
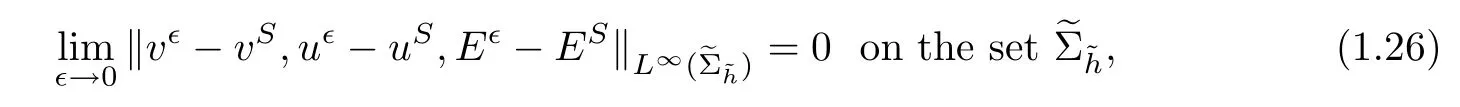
The outline of this paper is as follows.In Section 2,we give some known results about the viscous shock waves.In Section 3,we rewrite the original system and study it before the interaction time.In Section 4,we frst give some key lemmas and then obtain the desired estimate after the interaction time.

2 Preliminary
The aim of this section is to prepare for the proof of the main theorem.Now we give some background materials of system(1.1)with viscosity ǫ=1,

whereU=(v,u,E)T,here and hereafter,superscript T denotes the transpose and all vectors are column ones.Letri(U)andli(U)(i=1,2,3)be the right and left eigenvectors off′(U) such that
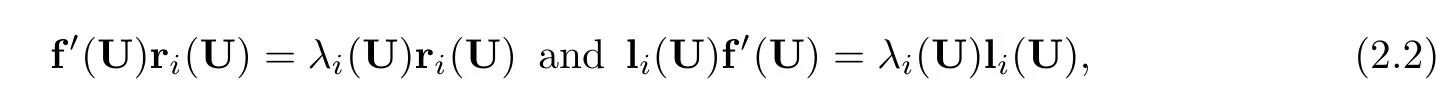
whererj(U)andli(U)satisfy that
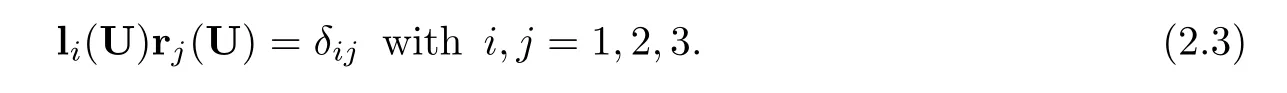
We denoteL,R,Λthe matrices in the following

Then we have

As we know,the viscous shock wave of system(2.1)has the form(v,u,E)(x,t)=U(ξ)= (v,u,E)(x−st).The 1-viscous shock waveUS1which connects(v∗,u∗,E∗)on the left and (v+,u+,E+)on the right exists uniquely up to a shift and satisfes

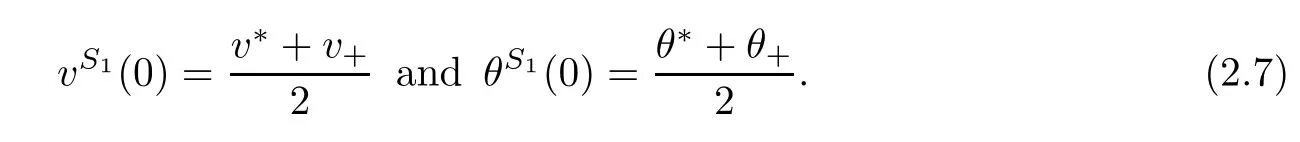
According to(2.6)1and(2.7),we can also get

Similarly,for the 3-viscous shockUS3wave connecting(v+,u+,E+)on the left and(v∗,u∗,E∗) on the right,it satisfes

with initial data satisfying

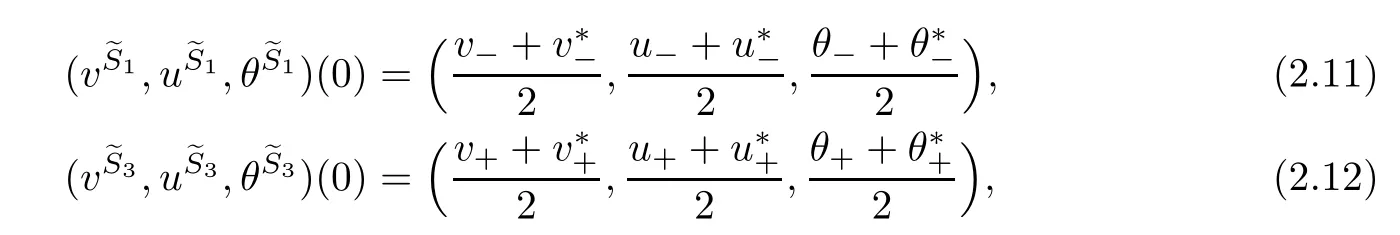
while for the 2-viscous outgoing contact discontinuityUeC=(veC,ueC,EeC)throughU∗−,is the integral curve associated with the vector feldr2(U)in the state space with the nonsingular
parameter˜ρ,satisfes

and the parameter˜ρ is chosen to satisfy
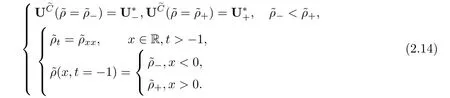
Then it is easy to check thatU˜Csatisfes
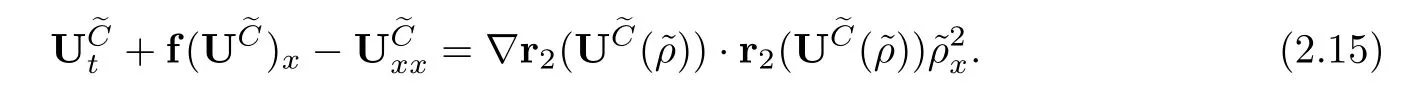
In order to makeUeCan exact solution,we assume the following structure condition

This structural condition was proposed frst in[18]and used in[11],[29]to study the stability of contact waves.For the contact discontinuity,in order to estimate the difcult termin Section 4,we give an elementary inequality concerning the heat kernel which will play an important role in Section 4.We defne
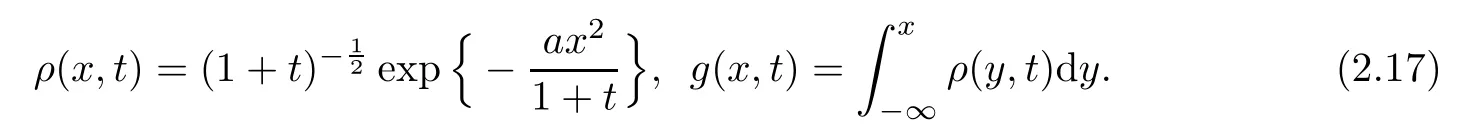
It is easy to fnd that
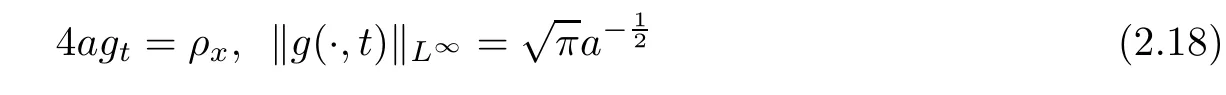
and we have the following lemma.
Lemma 2.1(Huang-Li-Matsumura inequality[9]) For 0 Then the following inequality holds For any ǫ>0,we defne the corresponding viscous shock wave of(1.1)in the following From[4,11]and[26],we can get the following lemma for the viscous contact discontinuity and viscous shock waves. Lemma 2.2There are positive constant C0and c0such that This section is devoted to estimates before the interacting time.For the purpose of convenience,in the following paper we will write the original problem in conservation law whereU=(v,u,E)T.To approximate the incoming shock waves,we defne for 0≤t≤t0, Let the above approximation at t=0 be the initial data of system(3.1),that is We defne it is easy to checkU(y,τ)holds that where By Lemma 2.2,we can obtain We want to study the above system by antiderivative technique(see[17,20]),So let φ(y,τ)=we have with initial data satisfying We look for the solution of the initial value problem(3.11),(3.12)in the following space: where I⊆R is any interval.Now we give the existence results of systems(3.11)and(3.12) before the interaction time,that is, Theorem 3.1(existence before the interaction time) There are constants δ0and C such that,if δ≤δ0,there exists a unique solutionw∈X(−t0ǫ,0)to(3.11)and(3.12).Furthermore, it holds that Since a local existence theorem is standard,if we want to prove Theorem 3.1,we only need to prove the following priori estimate.First,we need a priori assumption where[−t0ǫ,T]is the time interval on which the solution is assumed to exist,and η0is a small positive constant needs to be determined. Proposition 3.2(a priori estimate before the interaction time) Suppose that there exists a solutionwith T≤0,then there exist positive constants δ0,η0and C suchthat,if δ≤δ0and N(T)≤η0,thenwholds that for τ∈[−t0ǫ,T] In order to prove Proposition 3.2,we need to get the following lemmas.For the lower order estimates,we have Lemma 3.3Under the assumption of Proposition 3.2,there exists a small positive constant δ0and η0such that,if δ≤δ0and N(T)≤η0,then ProofAs the stability analysis for viscous wave[11,26,29],we frst construct the weighted functions.Let where with m=δ−1/2.By a simple calculation,we get Because of the strict hyperbolicity of the Euler equation,we can obtain c0<αi where First,we give the estimates of J in the following.Note that It is easy to check thatSimilar analysis towe obtain that As λ2≡0,we get thatwe have For the remaining term in J,we obtain By the above analysis,we have for suitable small δ, Second,we give the estimates of I2in the following At last,we give the estimates of I1.then we have The analysis of aijyields that where we chooseµso small such thatThen for small δ and η0,by(3.29),(3.30)and(3.32),we have Integrate the above inequality with respect to t over[−ǫt0,τ],we can obtain the following lower order estimate As for the right term of(3.34),we have estimate as follows So we complete the proof of Lemma 3.3. ? Now we proceed to the estimates of higher order derivatives.Apply∂yto system(3.11), we obtain Multiply the above equality by wTyand integrate the result over R yields that Integrate the above equality with respect to t over[−t0ǫ,0],and by using Cauchy inequality, Lemma 3.3 and the smallness of ǫ0and δ,we get thatSimilarly,for the estimate ofwyy,we obtain that With the help of(3.38),(3.39)and Lemma 3.3,we can conclude that So we compete the proof of Proposition 3.2. In this section,we continue to study the non-isentropic gas dynamics after the interaction time τ>0,that is with initial data has already been solved in Section 3.Unlike the previous section where the initial data atis well-chosen such that the perturbationhere the initial data for system(4.1)is determined by the solution obtained before the interaction time. If we choose may not be zero,therefore we can not use the antiderivative technique.Usually,we can modify the shock wave profles with suitable shifts such that the corresponding integral is zero.For this,let ν1=U∗−−U−,ν2=U∗+−U∗−and ν3=U+−U∗+,ν1,ν2and ν3are linearly independent in R.So there exists constants b1,b2and b3such thatI0=b1ν1+b2ν2+b3ν3. We defne From(3.12),we have already known that which implies that By a simple calculation,we can obtain Then,it yields that From[23],we have already known that Thus we can obtain However,for the shock waves,by using Lemma 2.2,one only has|[(UeS1−U−)−(US1−U∗)]+[(UeS3−U∗+)−(US3−U−)](y,τ=0)|=O(1)δe−cδ|y|for y∈R,which only gives kRy −∞([(UeS1−U−)−(US1−U∗)]+[(UeS3−U∗+)−(US3−U−)])(z,τ=0)dzk2=O(1)δ−1. This means when the shock strength is small enough,the initial anti-derivative of perturbation is very large after the interaction time.So better estimates are needed.Diferent from[13]and [22],we need the following key lemma frst. Lemma 4.1For shock waves of Euler equation,the following relations hold Under Lemma 4.1,we can have similar results of[13]and[22]as follows Lemma 4.2If the wave strength δ is suitable small,then for any fxed b1,it holds that where the positive constant Cb1≤Ce|b1|. ProofFirst,from[23],we know for suitable small δ,the strength between the incoming and the outgoing waves have the following relations It is obvious that from(2.6)we have By Lemma 4.1,we obtain that with where the relation“≈”means we omit the term O(1)δB1.As we get the above equation,we have used Lemma 2.2 and the following relations get from(1.7)and(2.6) Integrate(4.14)with respect to y over[y,0]with y<0,we have that where we have used the fact that vS1(0)=12(v∗+v+).Similar to vS1,we also can obtain the following relation for veS1, with It is easy to check that there exits constants c and C such that According to the above analysis,we can get the following better estimate The Gronwall’s inequality yields that Substitute it into(4.23),we can obtain that Thus we complete the proof of Lemma 4.2. ? Similar to Lemma 4.2,we have the following lemma. Lemma 4.3If the wave strength δ is suitable small,then for any fxed b1,b3,it holds that Based on(4.10),Lemma 4.2 and Lemma 4.3,one has the following better estimate on the antiderivative ofat the interaction time. Lemma 4.4It holds that Under the above analysis,we continue to study system(4.1)after the interaction time. Similar to Section 3,it is easy to know thateUsatisfes where Note that Claim ProofHere we just provethe other term can be proved similarly.By Lemma 2.2,when y that Similarly,we can easily prove when y>es12τ, By the above analysis,we prove the claim. We rewrite(4.1)–(4.28)as follows By Lemma 4.4,we have the estimate of the initial data at the interaction time as follows Now our existence result after the interaction time can be stated in the following. Theorem 4.5(existence after the interaction time) There are constants δ0and C such that,if δ≤δ0,there exists a unique solution v to(4.35)and(4.36).Furthermore,it holds that Similar to Section 3,we only need a priori estimate,frst we need the following priori assumption Proposition 4.6(a priori estimate after the interaction time) Suppose that there exists a solutionwith T≥0,then there exist positive constantsand C such that,holds that for τ∈[0,T], In order to prove Proposition 4.6,we need the following lemmas. Lemma 4.7Under the assumption of Proposition 4.6,there exists a small positive constant δ0andthen ProofSame as[11,26,29],we introduce the weighted function at frst. Letdiagsuch that where and where we have and also The same analysis with Section 3,we have the following relation For the remaining term ineJ,we have Similarly,we have and By the above analysis and the smallness of δ,we have The structure condition(2.16)and the above equation gives that Integrate the above inequality with respect to t over[0,τ]with τ>0 to obtain that For the last term on the right of(4.63),we have For the last term on the right of(4.63),similar to Section 3,we get The above analysis,the smallness of δ and Lemma 4.4 yields that So we complete the proof of Lemma 4.7. For the higher order estimates we can get the following lemma,here we omit its proof. Lemma 4.8Under the assumption of Proposition 4.6,there exists a small positive constantthen and By Lemma 4.7 and Lemma 4.8,we can prove Proposition 4.6 easily. Proof of Theorem 1.1Before the interaction time t0,asLemma 2.2 and Theorem 3.1 gives the convergence rate(1.25).After the interaction time t0,Theorem 4.5 and the factgives that Thus,Lemma 2.2 and the above equality prove convergence(1.26).The proof of Theorem 1.1 is completed. ? [1]Bianchini S,Bressan A.Vanishing viscosity solutions of nonlinear hyperbolic systems.Ann Math,2005, 161(1):223–342 [2]Bressan A,Huang F M,Wang Y,Yang T.On the convergence rate of vanishing viscosity approximations for nonlinear hyperbolic systems.SIAM J Math Anal,2012,44(5):3537–3563 [3]Bressan A,Yang T.On the convergence rate of vanishing viscosity approximations.Comm Pure Appl Math, 2004,57(8):1075–1109 [4]Goodman J.Nonlinear asymptotic stability of viscous shock profles for conservation laws.Arch Rational Mech Anal,1986,95(4):325–344 [5]Goodman J,Xin Z P.Viscous limits for piecewise smooth solutions to systems of conservation laws.Arch Rational Mech Anal,1992,121(3):235–265 [6]HofD,Liu T-P.The inviscid limit for the Navier-Stokes equations of compressible isentropic fow with shock data.Indiana Univ Math J,1989,38(4):861–915 [7]Huang F M,Jiang S,Wang Y.Zero dissipation limit of full compressible Navier-Stokes equations with a Riemann initial data.Commun Inf Syst,2013,13(2):211–246 [8]Huang F M,Li X.Zero dissipation limit to rarefaction waves for the 1-D compressible Navier-Stokes equations.Chin Ann Math Ser B,2012,33(3):385–394 [9]Huang F M,Li J,Matsumura A.Asymptotic stability of combination of viscous contact wave with rarefaction waves for one-dimensional compressible Navier-Stokes system.Arch Ration Mech Anal,2010,197(1): 89–116 [10]Huang F M,Matsumura A,Xin Z P.Stability of contact discontinuities for the 1-D compressible Navier-Stokes equations.Arch Ration Mech Anal,2006,179(1):55–77 [11]Huang F M,Pan R H,Wang Y.Stability of contact discontinuity for Jin-Xin relaxation system.J Difer Equ,2008,244(5):1114–1140 [12]Huang F M,Wang Y,Wang Y,Yang T.The limit of the Boltzmann equation to the Euler equations for Riemann problems.SIAM J Math Anal,2013,45(3):1741–1811 [13]Huang F M,Wang Y,Wang Y,Yang T.Vanishing viscosity of isentropic Navier-Stokes equations for interacting shocks.Sci China Math,2015,58(4):653–672 [14]Huang F M,Wang Y,Yang T.Vanishing viscosity limit of the compressible Navier-Stokes equations for solutions to a Riemann problem.Arch Ration Mech Anal,2012,203(2):379–413 [15]Huang F M,Xin Z P,Yang T.Contact discontinuity with general perturbations for gas motions.Adv Math, 2008,219(4):1246–1297 [16]Jiang S,Ni G X,Sun W J.Vanishing viscosity limit to rarefaction waves for the Navier-Stokes equations of one-dimensional compressible heat-conducting fuids.SIAM J Math Anal,2006,38(2):368–384 [17]Kawashima S,Matsumura A.Asymptotic stability of traveling wave solutions of systems for one-dimensional gas motion.Comm Math Phys,1985,101(1):97–127 [18]Liu T-P,Xin Z P.Pointwise decay to contact discontinuities for systems of viscous conservation laws.Asian J Math,1997,1(1):34–84 [19]Ma S X.Zero dissipation limit to strong contact discontinuity for the 1-D compressible Navier-Stokes equations.J Difer Equ,2010,248(1):95–110 [20]Matsumura A,Nishihara K.On the stability of travelling wave solutions of a one-dimensional model system for compressible viscous gas.Japan J Appl Math,1985,2(1):17–25 [21]Serre D.Global solutions(−∞ [22]Shi X D,Zhang Y L.Vanishing mean free path limit for interacting shock waves of broadwell equation.J Math Anal Appl,2015,432(2):868–887 [23]Smoller J.Shock Waves and Reaction-Difusion Equations.New York:Springer,1994 [24]Wang Y.Zero dissipation limit of the compressible heat-conducting Navier-Stokes equations in the presence of the shock.Acta Math Sci,2008,28B(4):727–748 [25]Xin Z P.Zero dissipation limit to rarefaction waves for the one-dimensional Navier-Stokes equations of compressible isentropic gases.Comm.Pure Appl.Math,1993,46(5):621–665 [26]Xin Z P.Theory of viscous conservation laws//Some Current Topics on Nonlinear Conservation Laws. AMS/IP Stud Adv Math,Vol 15.Providence,RI:Amer Math Soc,2000:141–193 [27]Yu S-H.Zero-dissipation limit of solutions with shocks for systems of hyperbolic conservation laws.Arch Ration Mech Anal,1999,146(4):275–370 [28]Zhang Y H,Pan R H,Wang Y,Tan Z.Zero dissipation limit with two interacting shocks of the 1D non-isentropic Navier-Stokes equations.Indiana Univ Math J,2013,62(1):249–309 [29]Zeng H H.Stability of a superposition of shock waves with contact discontinuities for systems of viscous conservation laws.J Difer Equ,2009,246(5):2081–2102 ∗Received June 3,2015;revised May 2,2016.The work of Xiaoding Shi was supported by National Natural Sciences Foundation of China(11471321).The work of Yan Yong was supported by National Natural Sciences Foundation of China(11201301).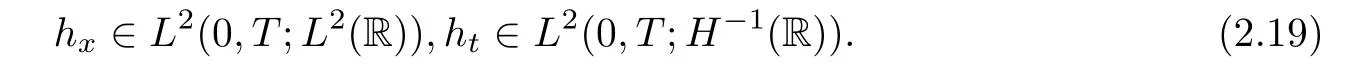
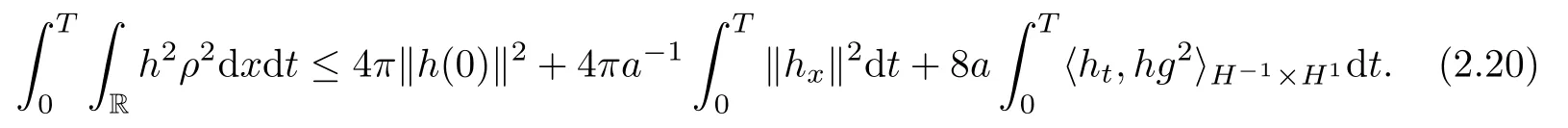

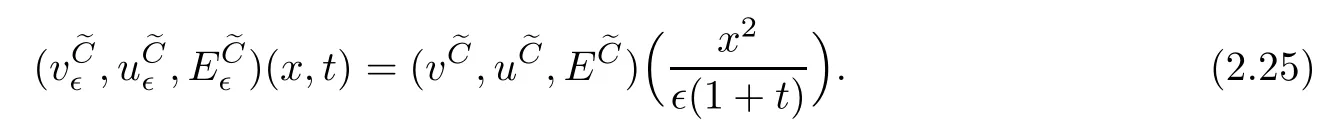

3 Estimates Before the Interacting Time



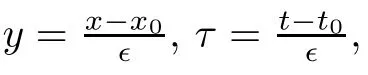





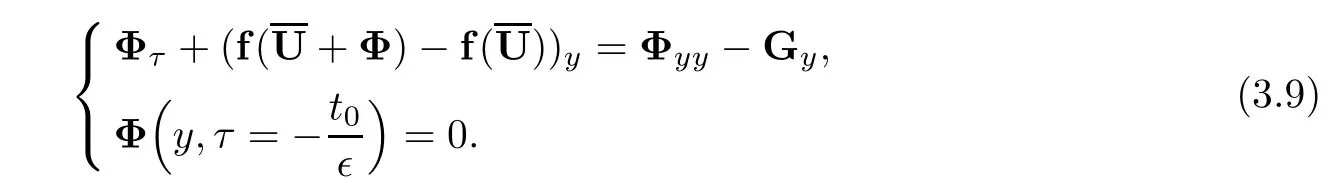



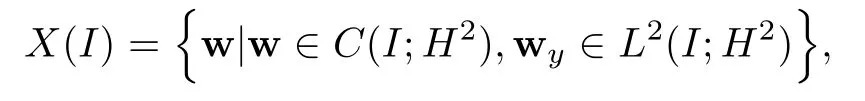
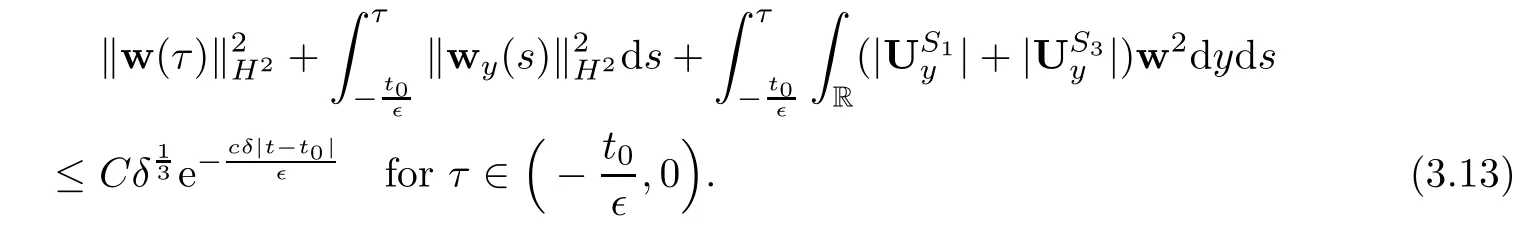
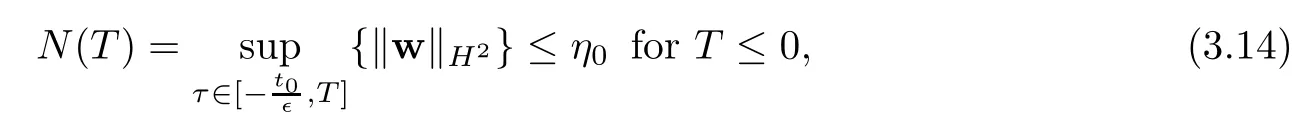
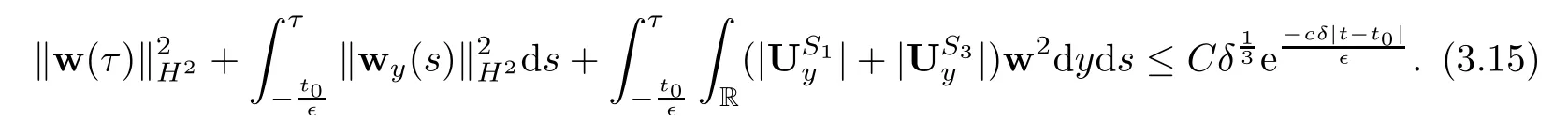
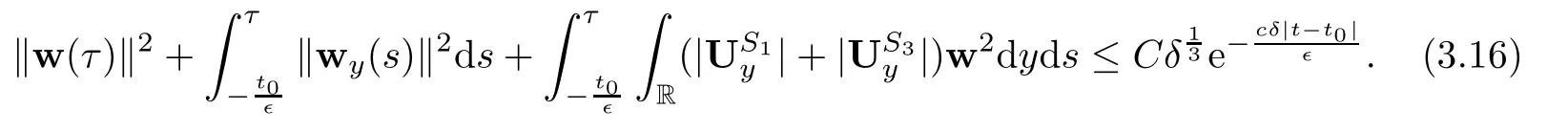

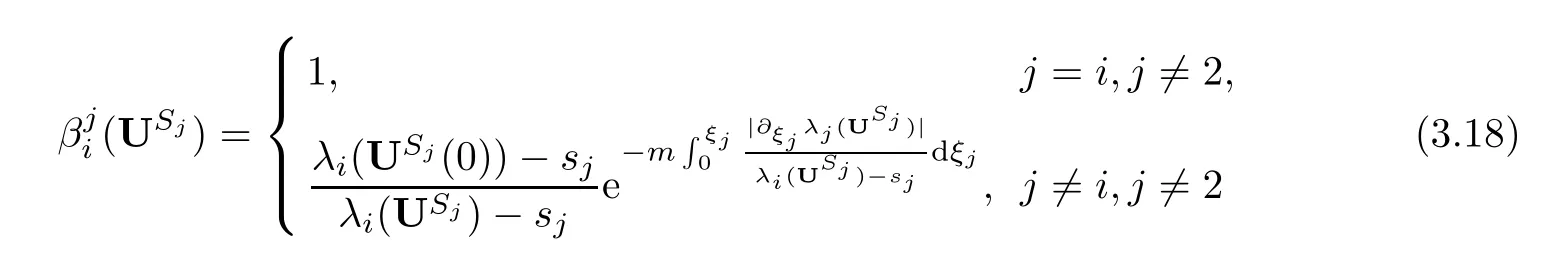


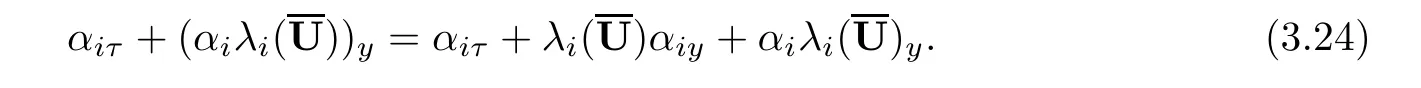
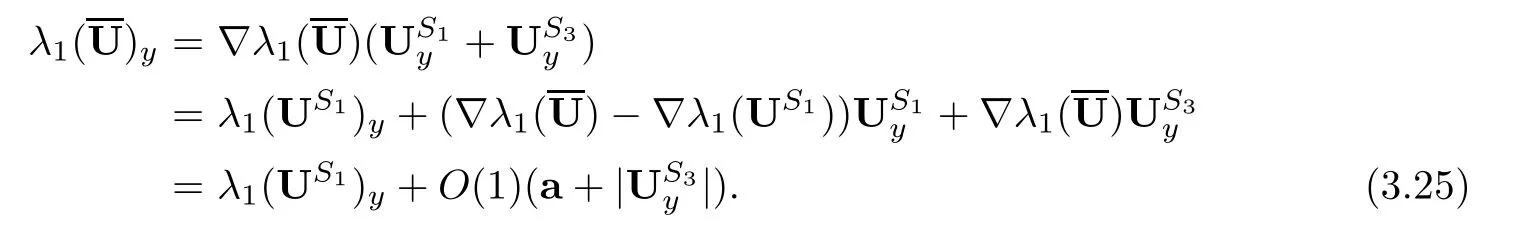

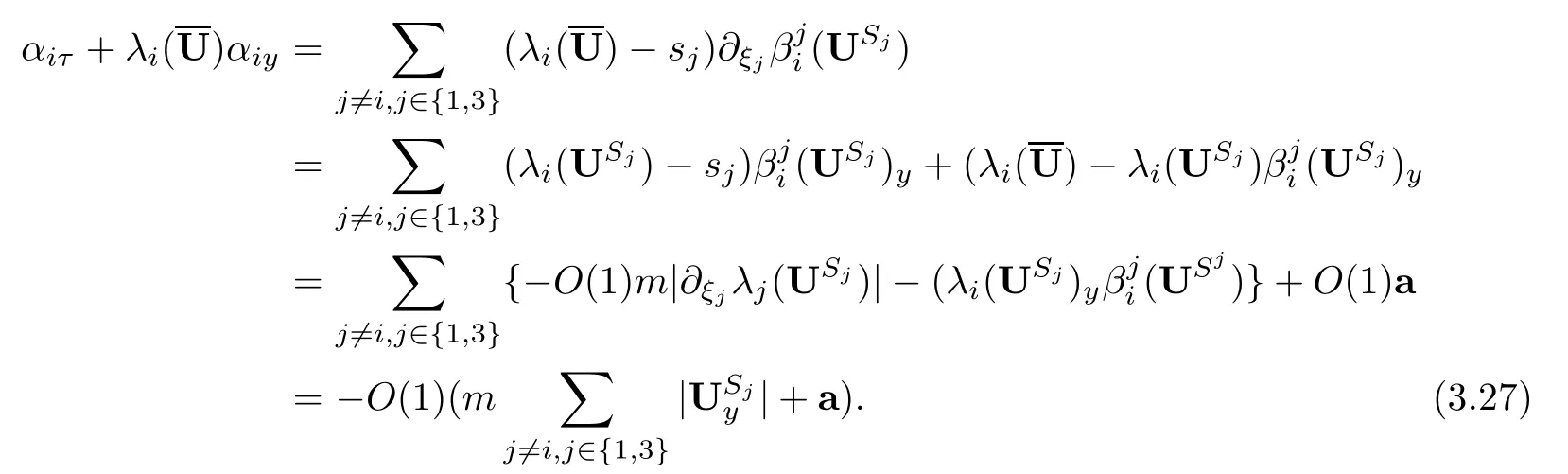
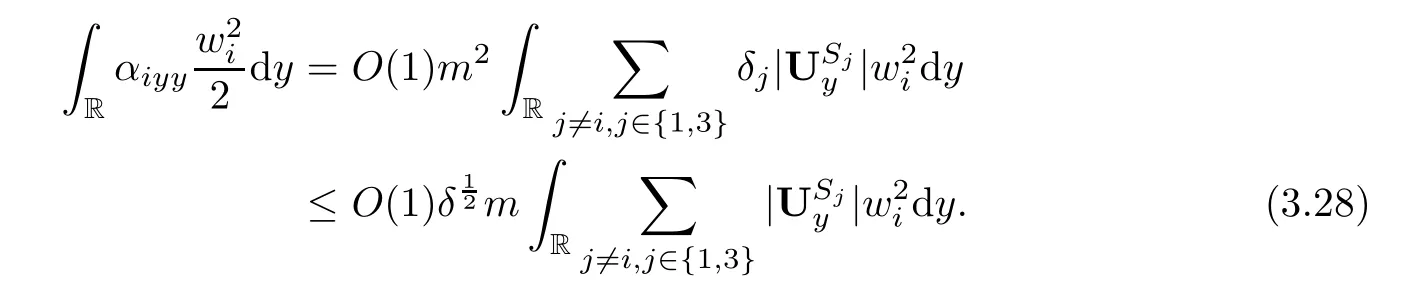
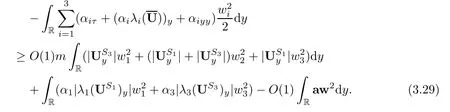
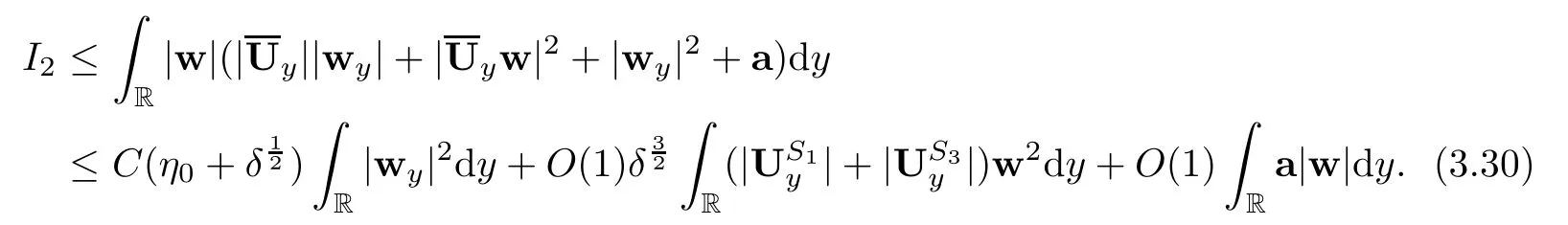



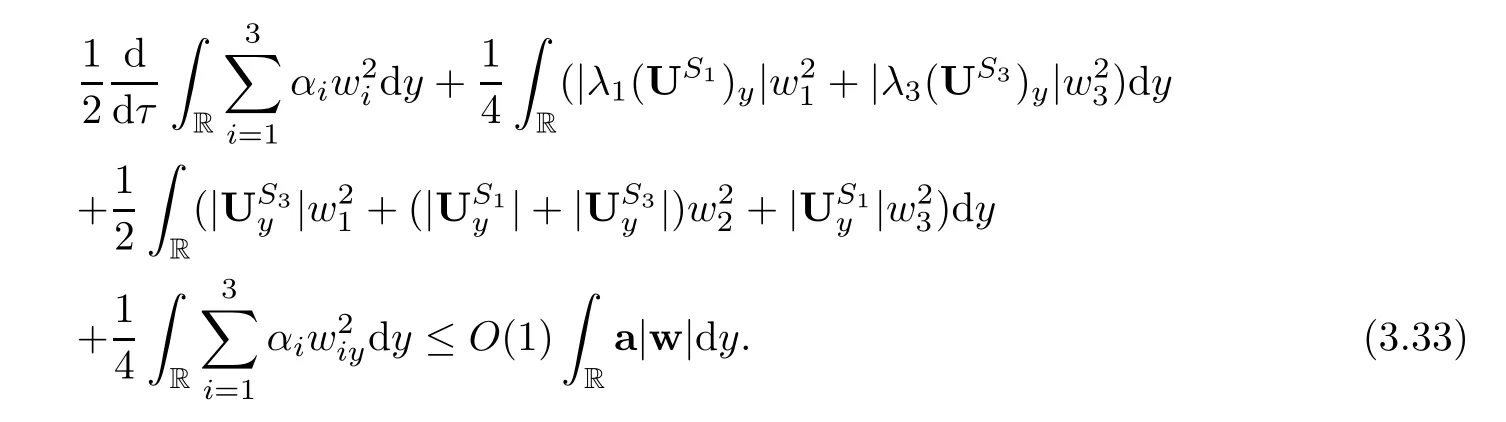
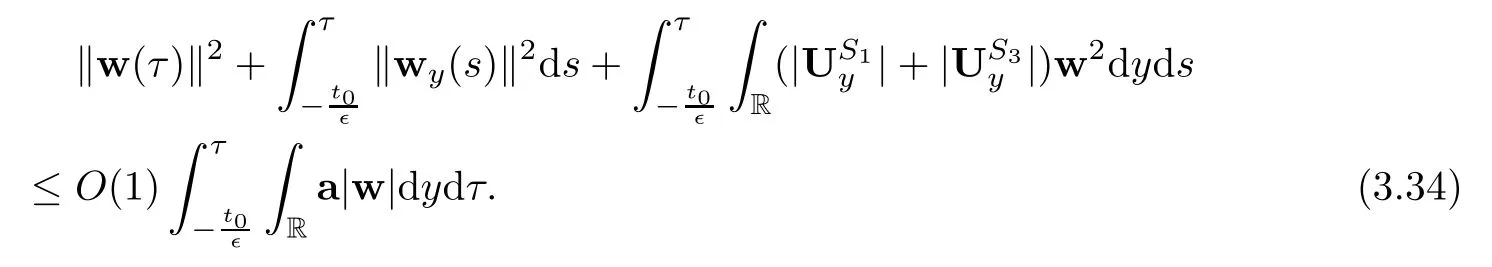
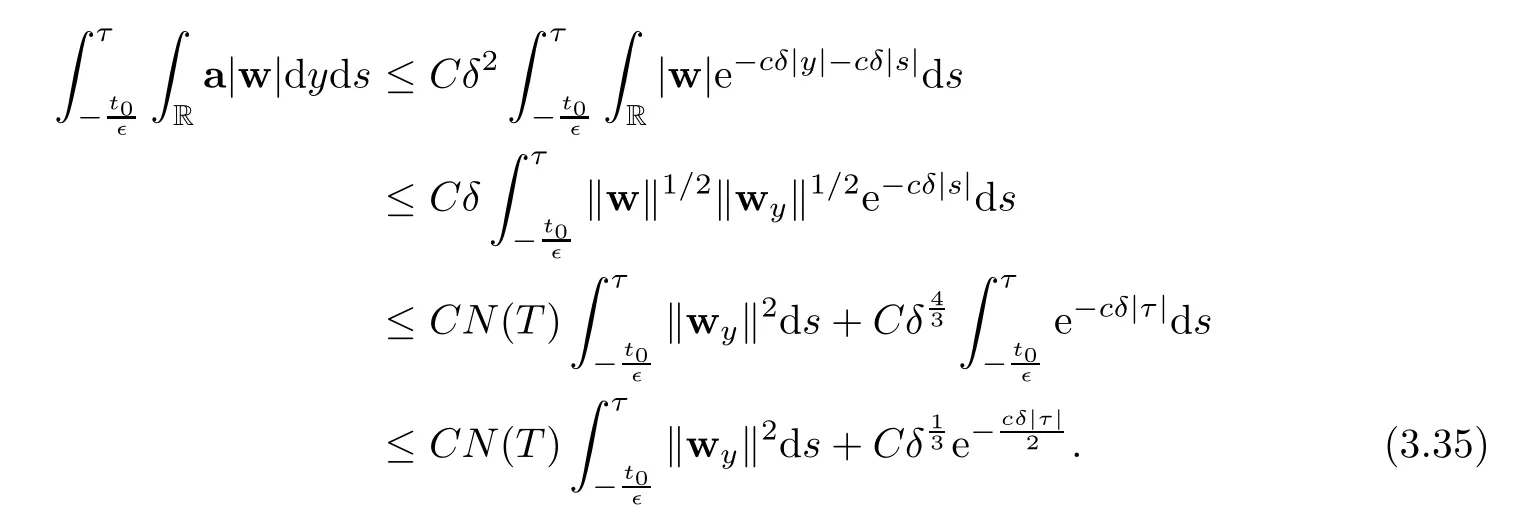

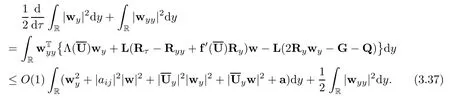

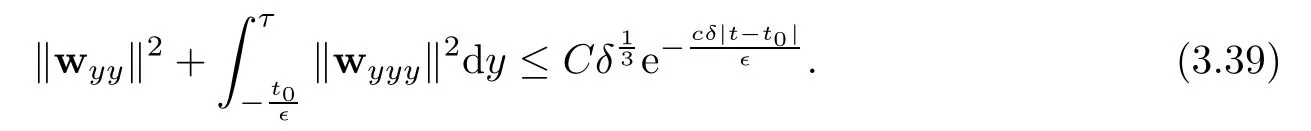
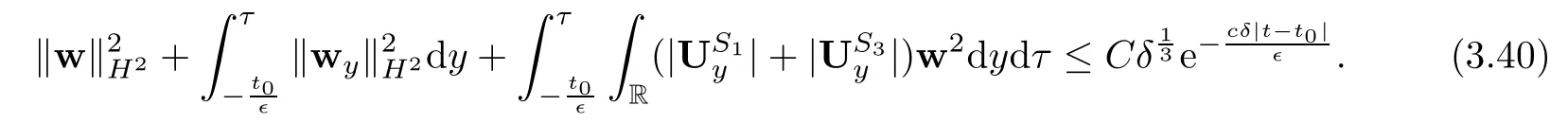
4 Estimates After the Interacting Time






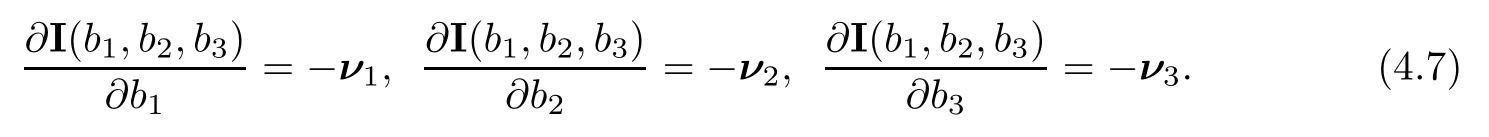

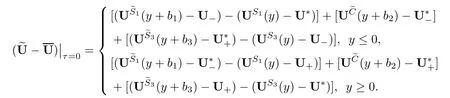
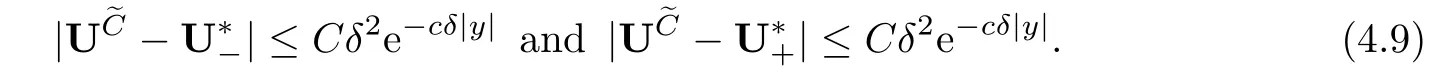

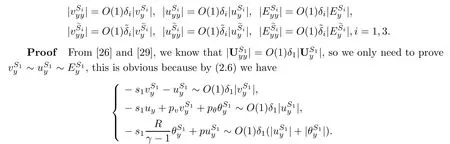

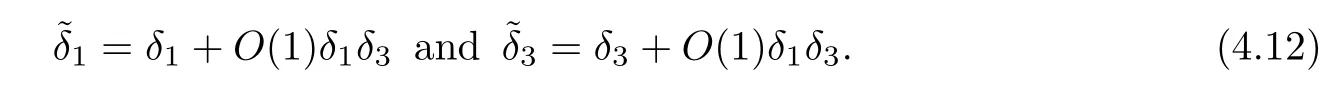

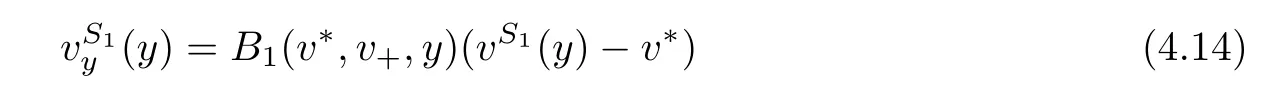
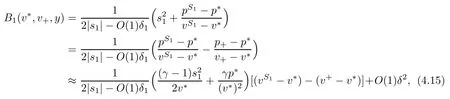


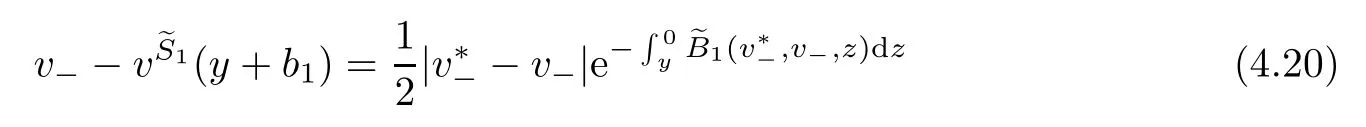
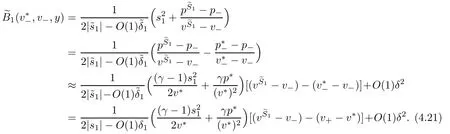
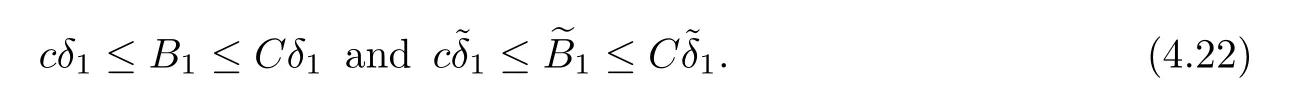
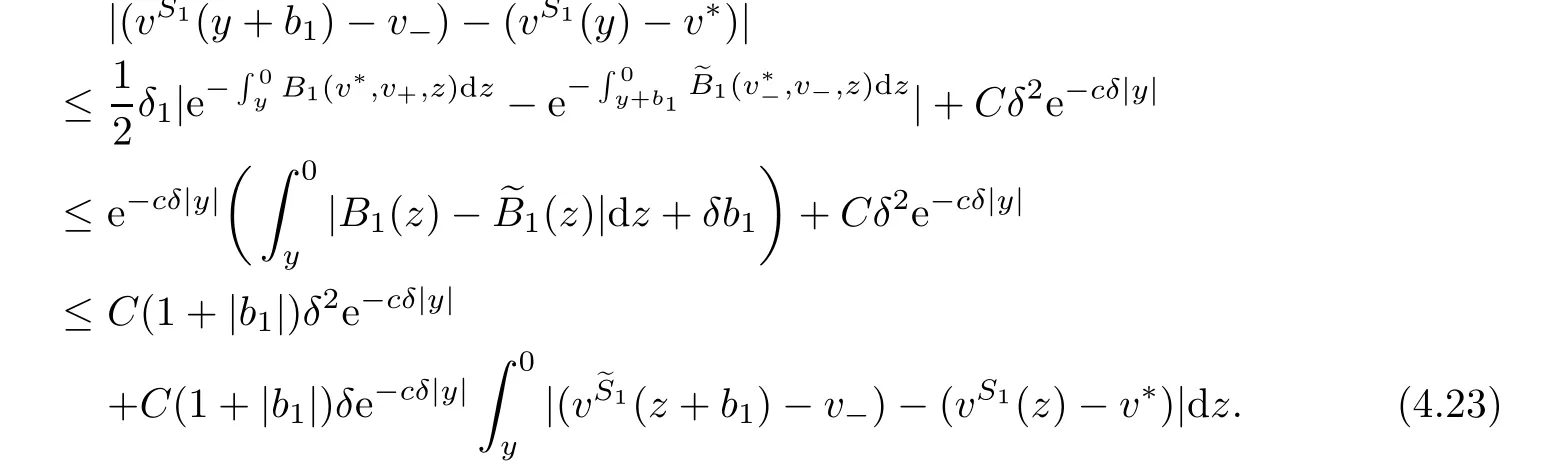
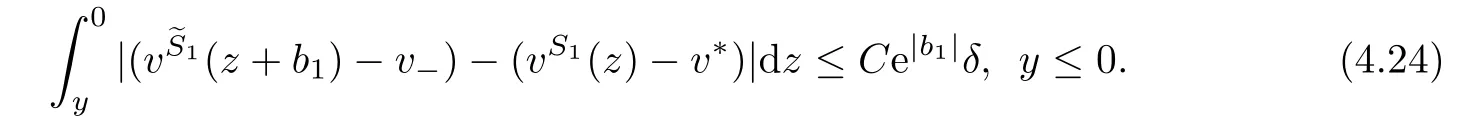



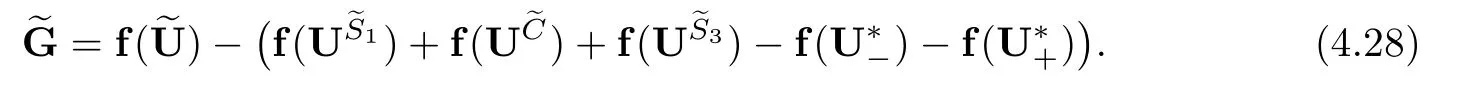


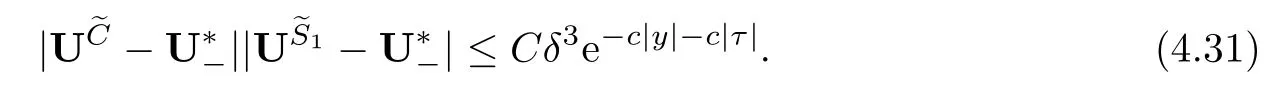
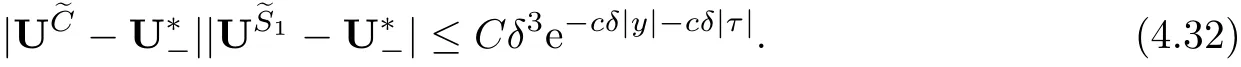
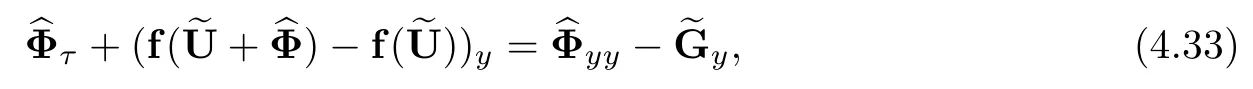
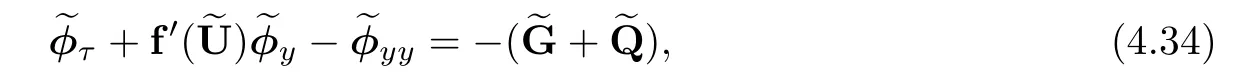
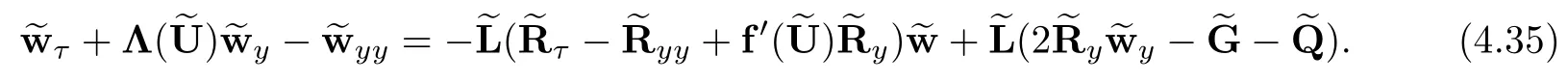

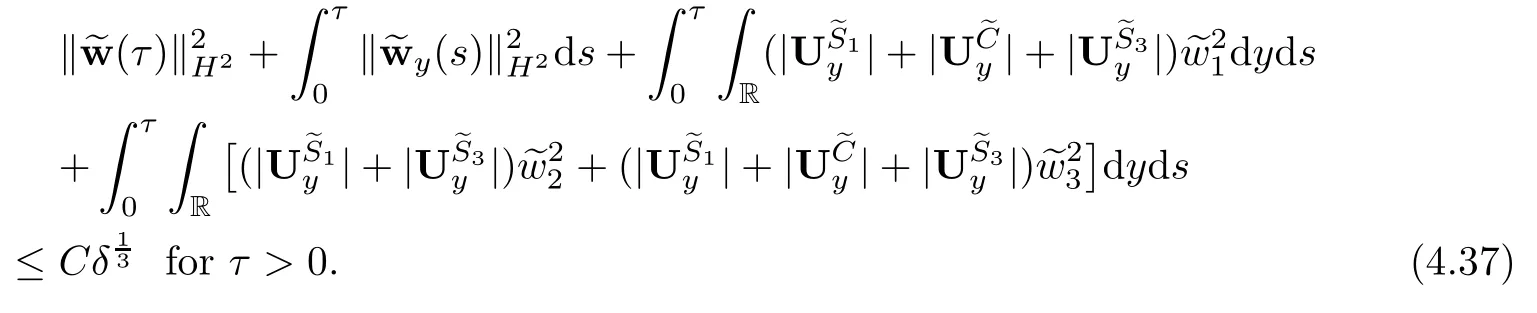
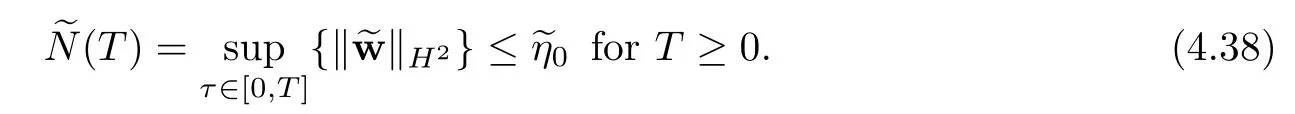






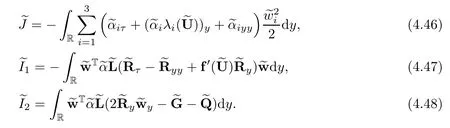


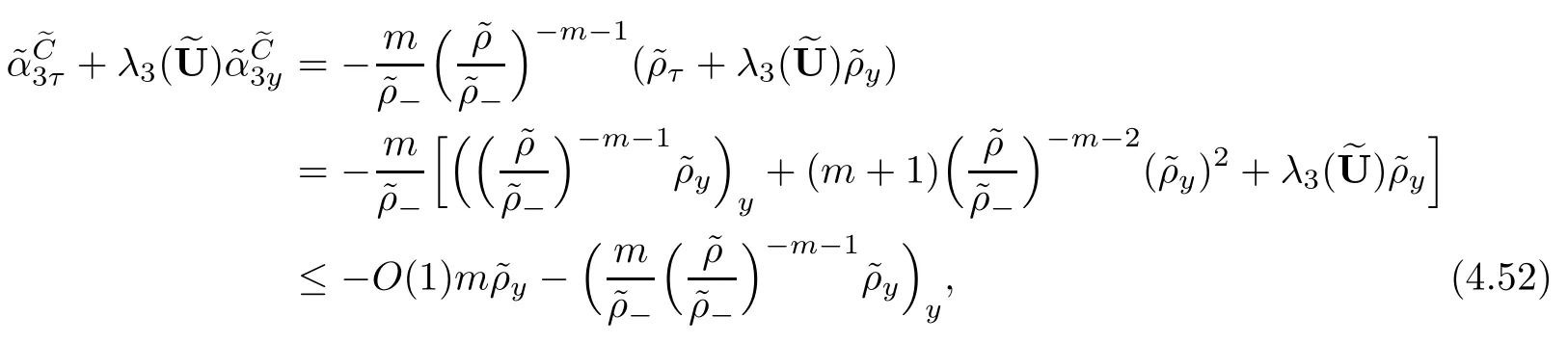



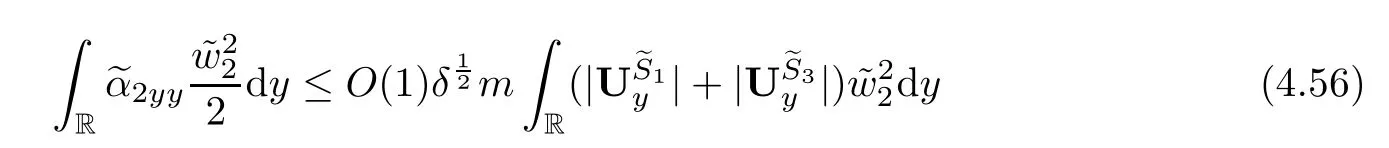


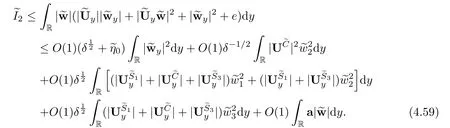

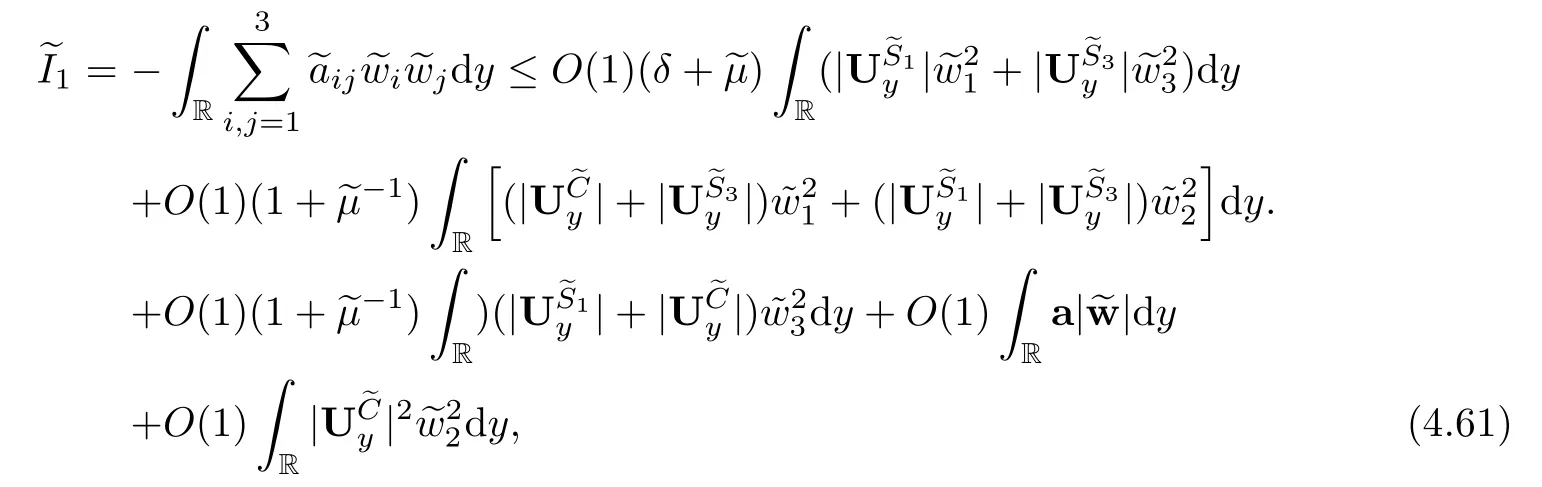
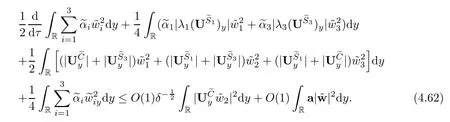
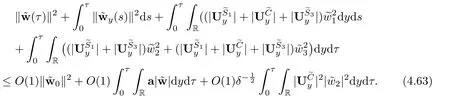

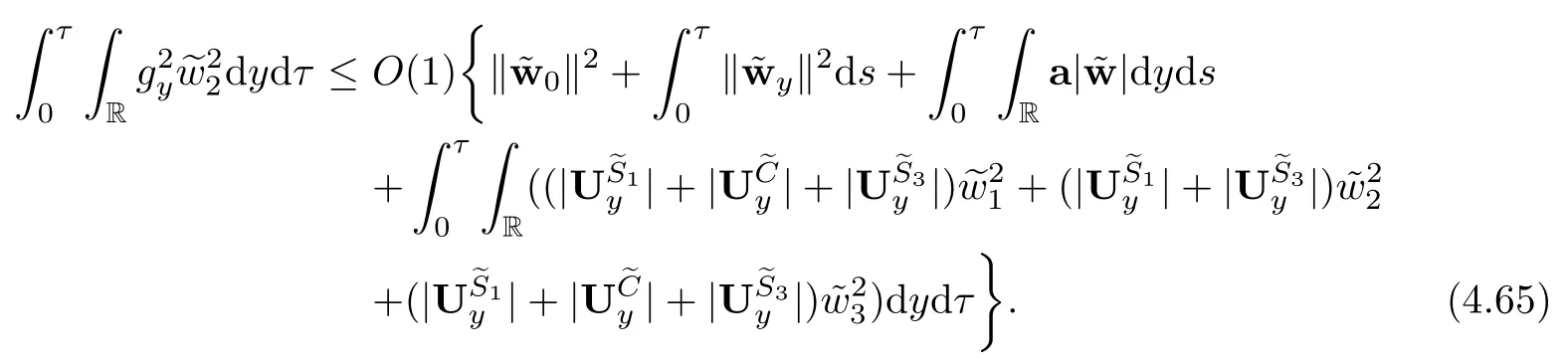


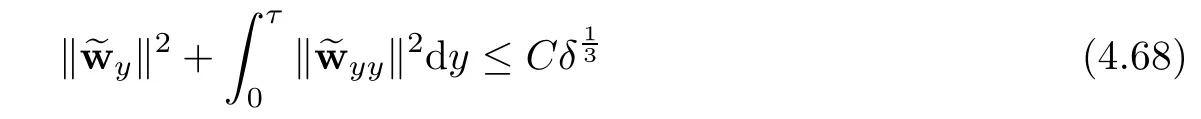
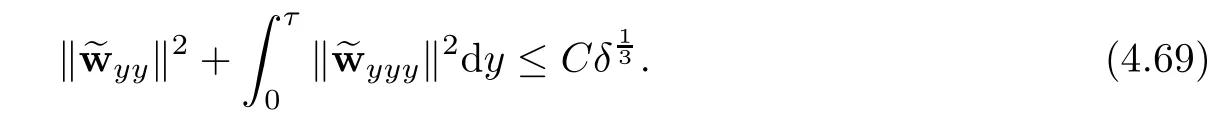

 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
