WEIGHTED PSEUDO ALMOST-PERIODIC SOLUTIONS OF SHUNTING INHIBITORY CELLULAR NEURAL NETWORKS WITH MIXED DELAYS∗

Mohammed Salah M’HAMDIChaouki AOUITIAbderrahmane TOUATI

Department of Mathematics,University of Carthage,Faculty of Sciences of Bizerta, BP W,7021 Zarzouna,Bizerta,Tunisia

Adel M.ALIMI

REGIM-lab:Research Groups on Intelligent Machines,University of Sfax,National Engineering School of Sfax(ENIS),BP 1173,Sfax 3038,Tunisia

Vaclav SNASEL

VSB Technical University of Ostrava,Czech Republic

WEIGHTED PSEUDO ALMOST-PERIODIC SOLUTIONS OF SHUNTING INHIBITORY CELLULAR NEURAL NETWORKS WITH MIXED DELAYS∗

Mohammed Salah M’HAMDIChaouki AOUITIAbderrahmane TOUATI

Department of Mathematics,University of Carthage,Faculty of Sciences of Bizerta, BP W,7021 Zarzouna,Bizerta,Tunisia

E-mail:mohammedsalah.mhamdi@yahoo.com;chaouki.aouiti@fsb.rnu.tn;Abder.Touati@fsb.rnu.tn

Adel M.ALIMI

REGIM-lab:Research Groups on Intelligent Machines,University of Sfax,National Engineering School of Sfax(ENIS),BP 1173,Sfax 3038,Tunisia

E-mail:adel.alimi@ieee.org

Vaclav SNASEL

VSB Technical University of Ostrava,Czech Republic

E-mail:vaclav.snasel@vsb.cz

In this paper,we prove the existence and the global exponential stability of the unique weighted pseudo almost-periodic solution of shunting inhibitory cellular neural networks with mixed time-varying delays comprising diferent discrete and distributed time delays.Some sufcient conditions are given for the existence and the global exponential stability of the weighted pseudo almost-periodic solution by employing fxed point theorem and diferential inequality techniques.The results of this paper complement the previously known ones.Finally,an illustrative example is given to demonstrate the efectiveness of our results.

weighted pseudo almost-periodic solution;shunting inhibitory cellular neural networks;mixed delays;global exponential stability

2010 MR Subject Classifcation34K05;92B20;34C27;34D20;34K40;47H10

1 Introduction

In the past few decades,the neural networks were studied extensively.There were many research results about the existence,uniqueness and stability of almost periodic,asymptotically almost periodic and pseudo-almost periodic solutions of neural network due to their potential application in classifcation,associative memory,parallel computation and other felds as mentioned in(see[4–9,11–14,16–20,23,26,27,37]).

As well known,both in biological and man-made neural networks,delays are inevitable, due to various reasons.For instance,time delays can be caused by the fnite switching speed of amplifer circuits in neural networks.Time delays in the neural networks make the dynamic behaviors become more complex,and may destabilize the stable equilibria and admit oscillations,bifurcation and chaos.Such application heavily depend on their dynamics,hence we investigate the dynamical behaviour of the neural networks.Thus,it is very important to study the dynamics of neural networks delay.

Cellular neural networks(CNNs)showed great potential as information-processing systems. Recently,many authors paid much attention to the research on the theory and application of the CNNs.The Shunting Inhibitory Artifcial Neural Networks(SIANNs)are a new class of CNNs and are biologically inspired networks in which the synaptic interactions among neurons are mediated via a nonlinear mechanism called shunting inhibition,which equips neurons with a gain control mechanism that allows them to operate as adaptive nonlinear flters.Since Bouzerdout and Pinter in(see[1])described SICNNs as a new cellular neural networks(CNNs), SICNNs were extensively applied in psychophysics,speech,perception,robotics,adaptive pattern recognition,vision,and image processing.In this paper,we consider the following models for shunting inhibitory cellular neural networks with mixed delays as follows

The mixed delays include time-varying delays and unbounded distributed delays.Model(1.1) was the subject of intensive analysis by numerous authors in recent years.In particular,there were extensive results on the problems of the exponential convergence of solution of SICNNs [21],the existence and stability of almost periodic and positive almost periodic solutions of SICNNs(see[2,3,10,22,24,25,33–35])and the existence and stability of pseudo almostperiodic solutions of SICNNs(see[15,31]).Here we introduce a new class of functions called weighted pseudo-almost periodic functions(see[28–30,32])generalized pseudo-almost periodic and almost periodic functions.The main idea is to put a weight(a locally integrable function on all R),on ergodic component appearing in[2,31]and obtain the weight space.In this way, a pseudo-almost-periodic function with weight appear as a perturbation of an almost-periodic function by an ergodic component of the weight space.Since the space of weighted pseudo almost-periodic functions contains strictly the space of pseudo almost-periodic,almost-periodic and periodic functions,the criteria obtained in this paper extend and improve the results given by Anping Chen and Jinde Cao in[2].

The rest of this paper is organized as follows.In Section 2,we will recall the basic properties of the weighted pseudo almost-periodic functions.In Section 3,we will introduce some necessary notations,defnitions,and preliminaries that will be used later.The existence and the uniqueness of weighted pseudo almost-periodic solutions of(1.1)in the suitable convex set arediscussed in Section 4.A numerical example is given in Section 5 to illustrate the efectiveness of our results.Finally,we draw conclusion in Section 6.

2 Weighted Pseudo Almost Periodic Functions

Throughout this paper,we denote Rn(R1=R)the set of all n-dimensional real vectors (real numbers),and we will use the following concepts and notations.BC(R,Rn)denotes the set of bounded continuous functions from R to Rn.Note that(BC(R,Rn),k.k∞)is a Banach space where k.k∞denotes the sup norm

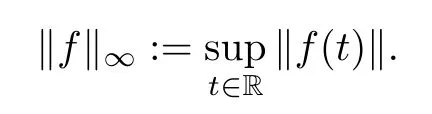
Let U denote the collection of functions(weights)ρ:R 7−→(0,∞)which are locally integrable over R such that ρ>0 almost everywhere.From now on,if ρ∈U and for T>0,we then set

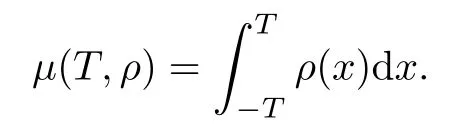
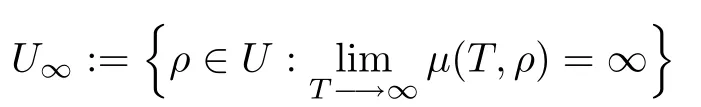
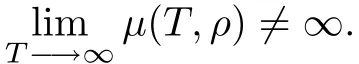
Obviously,UB⊂U∞⊂U,with strict inclusions.

Remark 2.1(1)Setting ρ1(x)=for each x∈R,it is easy to see that ρ1∈U,and 1≤ρ1≤2 for each x∈R,and hence ρ1∈UB.

(2)Setting ρ2(x)=exfor each x∈R.It is not difcult to see that ρ2∈U∞−UB.

Defnition 2.2(see[28]) A function f∈C(R,Rn)is called(Bohr)almost periodic if for each ε>0 there exists L(ε)>0 such that every interval of length L(ε)>0 contains a number τ with the property that

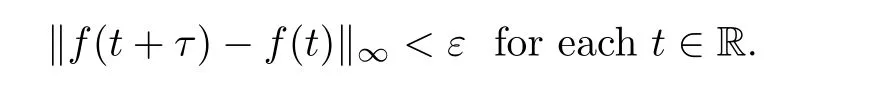
The number τ above is called an ε-translation number of f,and the collection of all such functions will be denoted as AP(R,Rn).

To introduce those weighted pseudo-almost periodic functions,we need to defne the weighted ergodic space PAP0(R,Rn,ρ).Weighted pseudo-almost periodic functions will then appear as perturbations of almost periodic functions by elements of PAP0(R,Rn,ρ).

Let ρ∈U∞.DefneClearly,when ρ(x)=1 for each x∈R,one retrieves the so-called ergodic space of Zhang,that is,PAP0(R,Rn),defned by

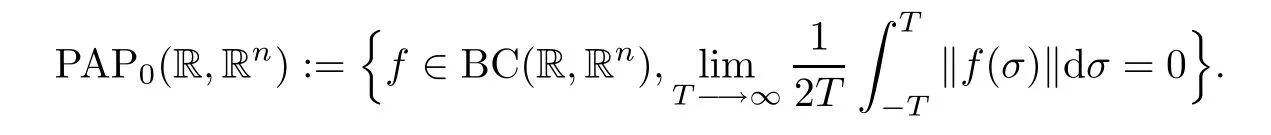
Clearly,the spaces PAP0(R,Rn,ρ)are richer than PAP0(R,Rn)and give rise to an enlarged space of pseudo-almost periodic functions.

We are now ready to defne weighted pseudo-almost periodic functions.

Defnition 2.3(see[29]) Let ρ∈U∞.A function f∈BC(R,Rn)is called weighted pseudo-almost periodic(or ρ-pseudo almost periodic)if it can be expressed as f=g+φ,where g∈AP(R,Rn)and φ∈PAP0(R,Rn,ρ).The collection of such functions will be denoted by PAP(R,Rn,ρ).

The initial conditions associated with(1.1)are of the form

where ϕij(.)are real-valued bounded continuous functions defned on(−∞,0],and we defne the norm

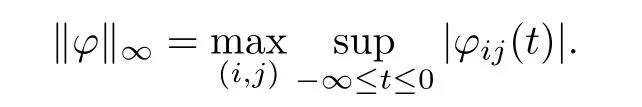
Defnition 2.4(see[8]) Letbe a weighted pseudo-almost periodic solution of system(1.1)with initial value

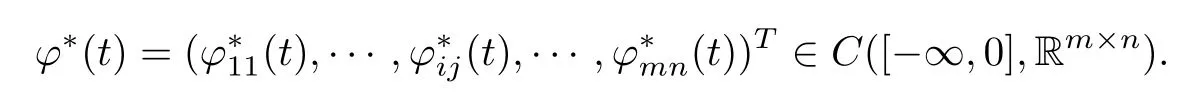
If there exist constants λ>0 and M(ϕ)>1 such that for every solution x(t)=(x11(t),···, xij(t),···,xmn(t))Tof system(1.1)with any initial value

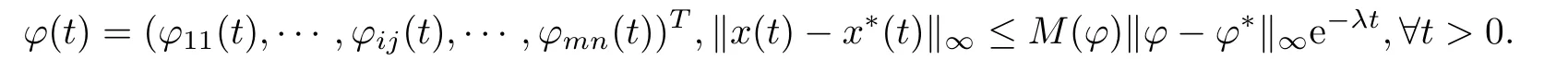
Then x∗(t)is globally exponential stable.

Remark 2.5(see[29]) (i)The functions g and φ in Defnition 2 are respectively called the almost periodic and the weighted ergodic perturbation components of f.

(ii)It is not hard to see that PAP0(R,Rn,ρ)is a closed subspace of(BC(R,Rn),k.k∞). This yields that(PAP(R,Rn,ρ),k.k∞)is a Banach space.

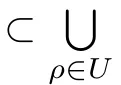
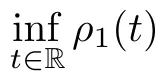
Lemma 2.7(see[22]) Let ci(t)be an almost periodic function on R and

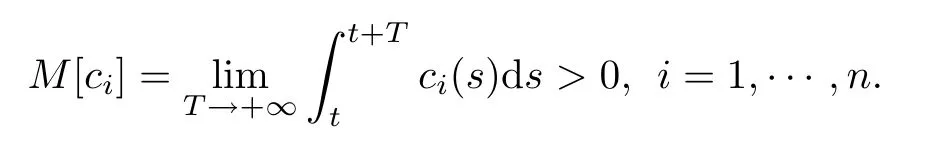
Then the linear system

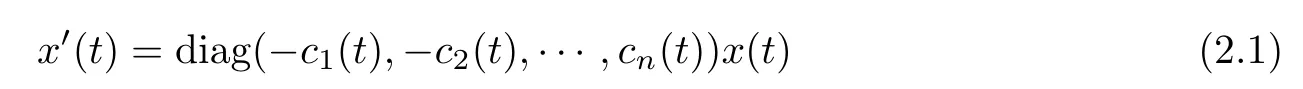
admits an exponential dichotomy on R.

Lemma 2.8(see[38]) The inhomogeneous linear system

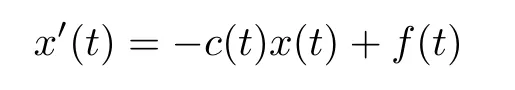
has a unique bounded solution for a vector f∈C(R,R)if and only if the inhomogeneous linear system(2.1)has exponential dichotomy.

3 Description of the System and Preliminaries

The model of the delayed shunting inhibitory cellular neural networks considered in this paper is described by the following state equations

where Cijdenotes the cell at the(i,j)position of the lattice.The r-neighborhood Nr(i,j)of Cijis given as

where Nq(i,j)and Np(i,j)are similarly specifed,xij(.)is the activity of the cell Cij,Lij(.)is the external input to Cij,aij(.)>0 represents the passive decay rate of the cell activity,are the connection or coupling strength of postsynaptic activity of the cell transmitted to the cell Cij,and the activity functions g(.),h(.)and f(.)are continuous functions representing the output or fring rate of the cell Ckl,τ(.)corresponds to the transmission time varying delay and 0≤τ(.)≤τ+.

Throughout this paper,we make the following assumptions.

(H1)There exist positive constant numbers Lg,Lh,Lf>0 such that for all x,y∈R,

and g(u)≤Mg,h(u)≤Mh,f(u)≤Mffor all u∈R.Furthermore,we suppose that g(0)= h(0)=f(0)=0.

(H2)For all 1≤i≤m,1≤j≤n,the delay kernels Kij:[0,∞)−→[0,∞)are bounded continuous,integrable and satisfy

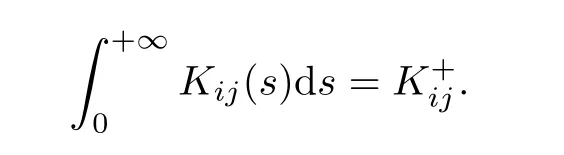
(H3)Let ρ:R 7−→(0,+∞),ρ∈U∞is continuous and assume

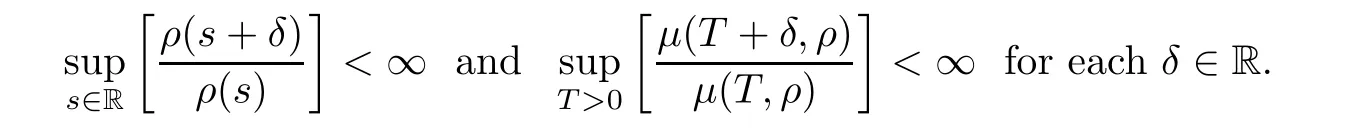
(H4) For all 1≤i≤m,1≤j≤n the functionsare weighted pseudo almost-periodic,and the functions t 7−→ aij(t)are almost periodic

4 Main Results

In this section,we establish some results for the existence,uniqueness,and the global exponential stability of the ρ-pseudo almost-periodic solution of(1.1).For convenience,we introduce the following notations:

Lemma 4.1Suppose that assumptions(H3)hold.If ϕ(.)∈PAP(R,Rm×n,ρ),then ϕ(.−h)∈PAP(R,Rm×n,ρ).

ProofBy defnition,we can write ϕ=ϕ1+ϕ2where ϕ1∈AP(R,Rm×n)and ϕ2∈PAP0(R,Rm×n,ρ).Obviously ϕ(.−h)=ϕ1(.−h)+ϕ2(.−h),ϕ1(.−h)∈AP(R,Rm×n)holds (see[6]),and for each h∈R,h≥0,we have

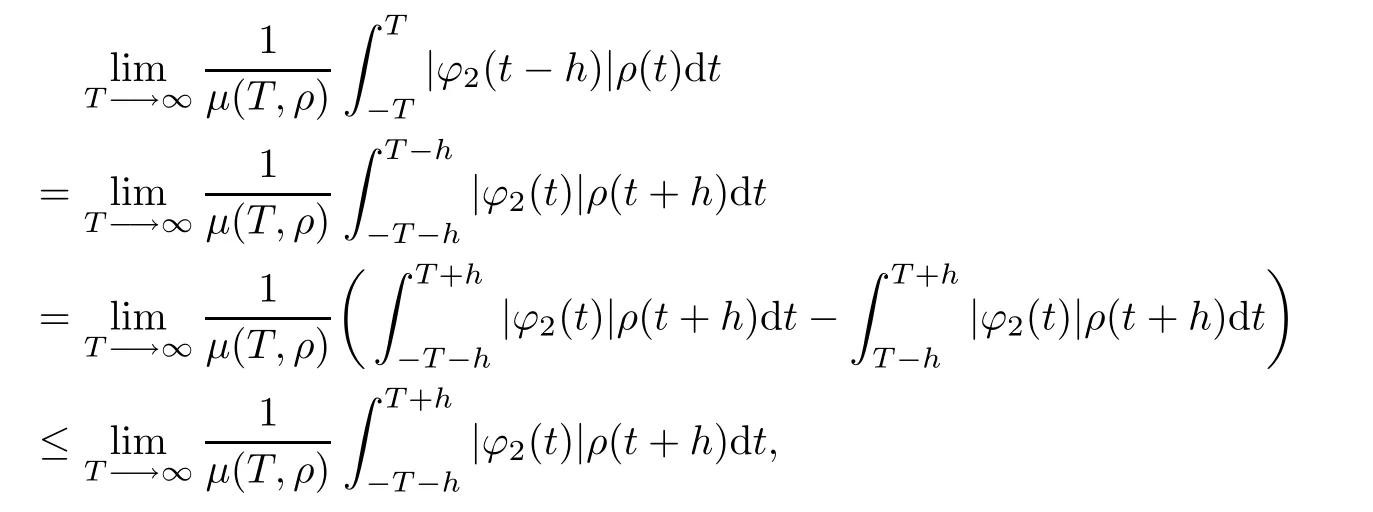
and for each h∈R,h≤0,we have

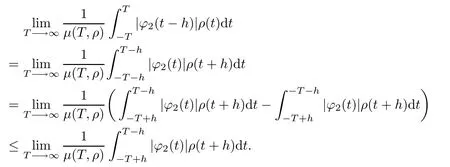
So we obtain

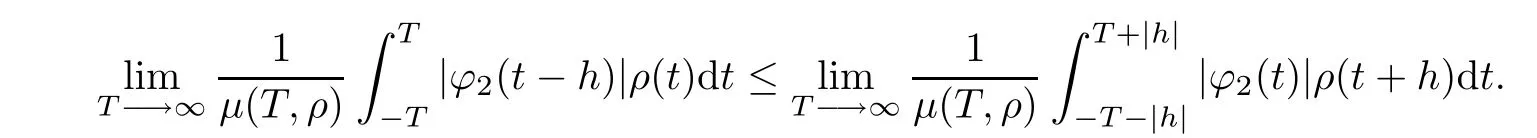
It follows from condition(H3)that

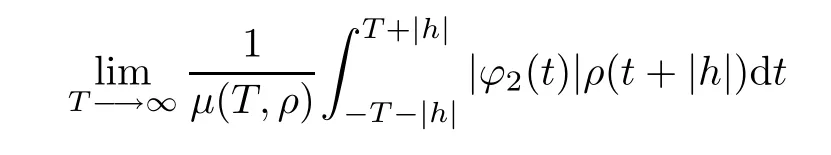
from which ϕ2∈PAP0(R,Rm×n,ρ),then ϕ∈PAP(R,Rm×n,ρ).The space PAP(R,Rm×n,ρ) is translation invariant. ?

Lemma 4.2If ϕ,ψ∈PAP(R,R,ρ),then ϕ×ψ∈PAP(R,R,ρ).

ProofBy defnition,we can write ϕ=ϕ1+ϕ2,ψ=ψ1+ψ2where ϕ1,ψ1∈AP(R,R) and ϕ2,ψ2∈PAP0(R,R,ρ).Obviously

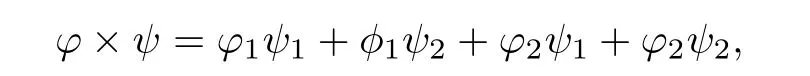
ϕ1ψ1∈AP(R,R)holds(see[6]),and for[φ1ψ2+ϕ2ψ1+ϕ2ψ2]we have

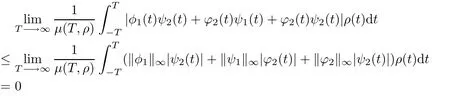
from which[φ1ψ2+ϕ2ψ1+ϕ2ψ2]∈PAP0(R,R,ρ).Then ϕ×ψ∈PAP(R,R,ρ).

Theorem 4.3Assume that assumptions(H1)–(H3)hold and for all 1≤k≤m,1≤l≤n,xkl(.)∈PAP(R,R,ρ),then for all 1≤i≤m,1≤j≤n the function φij:t 7−→

ProofFirst,the function φijsatisfes

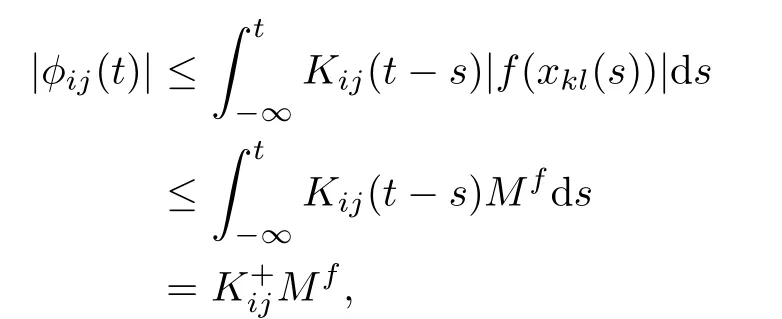
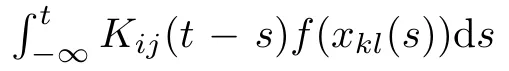
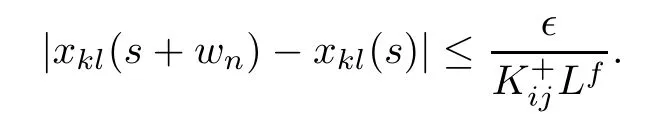
We have

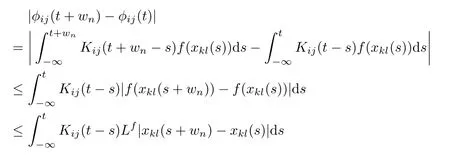
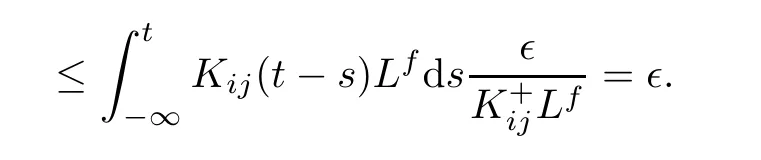
It remains to be proven whether the function φijbelongs to PAP(R,R,ρ).First,note that by using respectively the composition theorem of weighted pseudo almost-periodic functions(see [28])f(xkl(.))∈PAP(R,R,ρ)for all 1≤k≤m,1≤l≤n.

By the decomposition theorem of weighted pseudo almost-periodic functions(see[30]),we have

where ukl∈AP(R,R)and vkl∈PAP0(R,R,ρ).Consequently

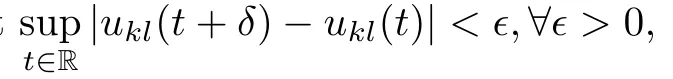
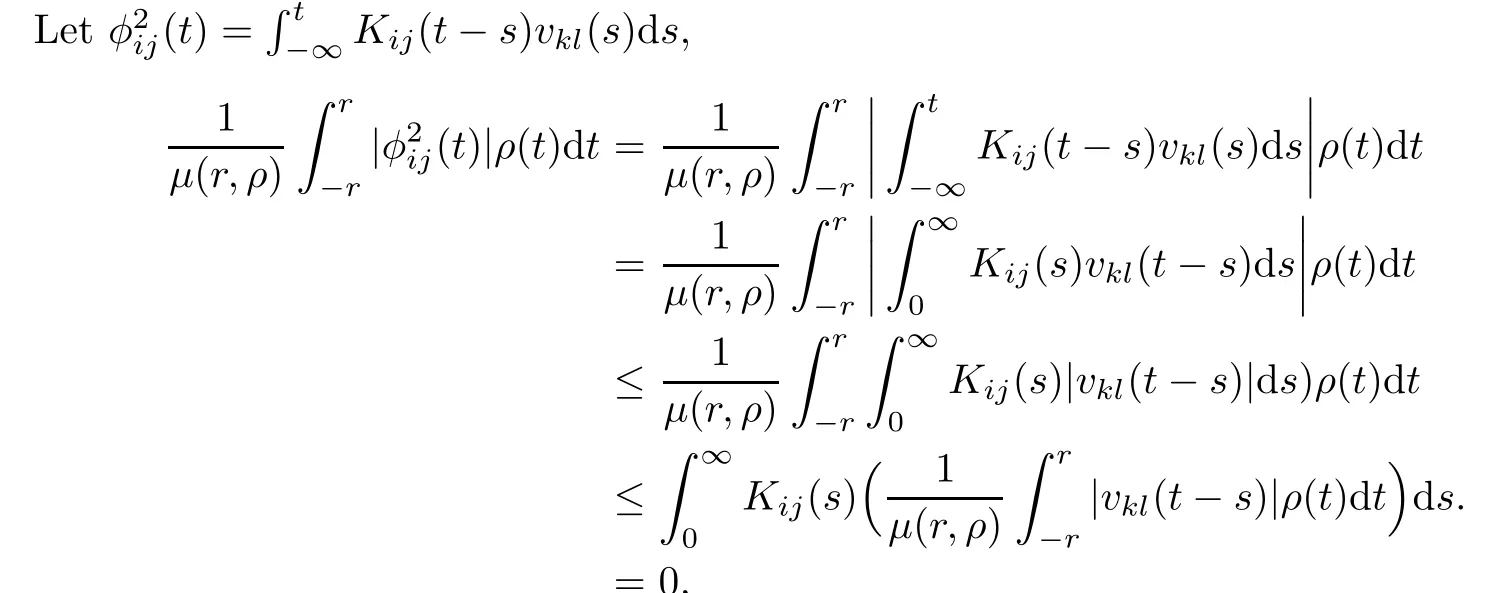
Lemma 4.4If h∈C(R,R)satisfes the Lipschitcz condition,ϕ∈PAP(R,R,ρ)and θ∈C(R,R),then h(ϕ(.−θ(.)))∈PAP(R,R,ρ).

ProofWe have ϕ=ϕ1+ϕ2,where ϕ1∈AP(R,R)and ϕ2∈PAP0(R,R,ρ).Let E(t)=h(ϕ1(t−θ(t))+[h(ϕ1(t−θ(t))+ϕ2(t−θ(t))−h(ϕ1(t−θ(t))] =E1(t)+E2(t).

First,it follows from Theorem 2.11 in[36]that E1(t)∈AP(R,R).Then,we show that E2(t)∈PAP0(R,R,ρ)because

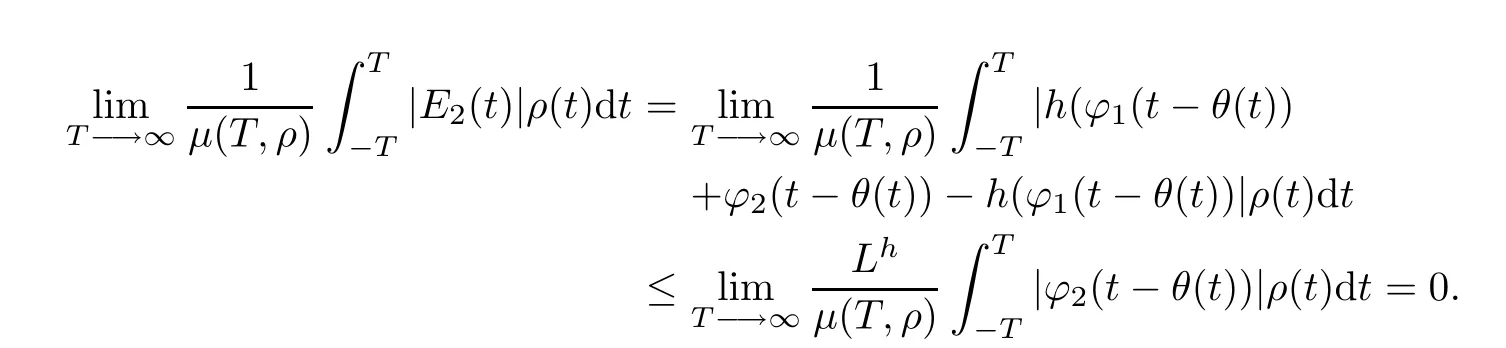
Thus E2(.)∈PAP0(R,R,ρ).So E(.)∈PAP(R,R,ρ).The proof is completed.

Lemma 4.5Suppose that assumptions(H1)–(H4)hold,and

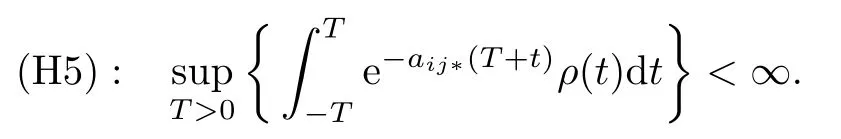
Defne the nonlinear operator Γ as follows,for each ϕ=(ϕ11,···,ϕij,···,ϕmn)∈PAP(R,Rm×n,ρ), (Γϕ)(t):=xϕ(t)where

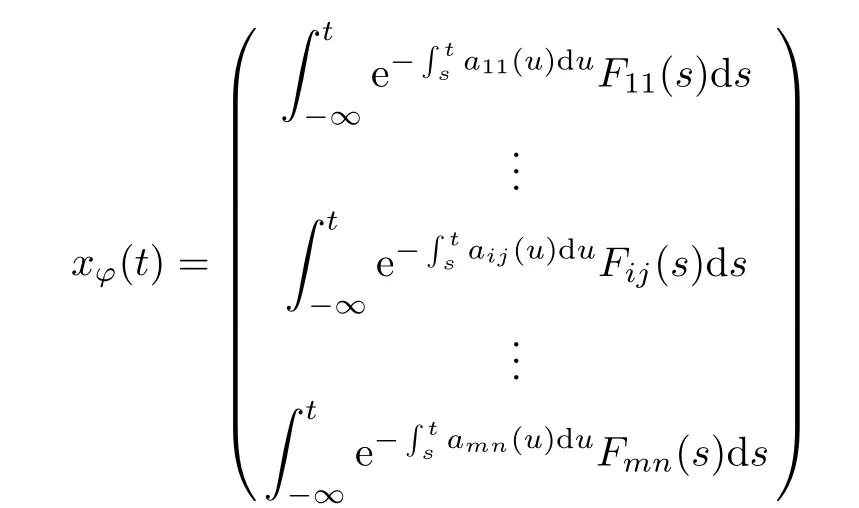
and

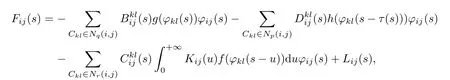
ProofFirst,note that,for all 1≤i≤m,1≤j≤n the function

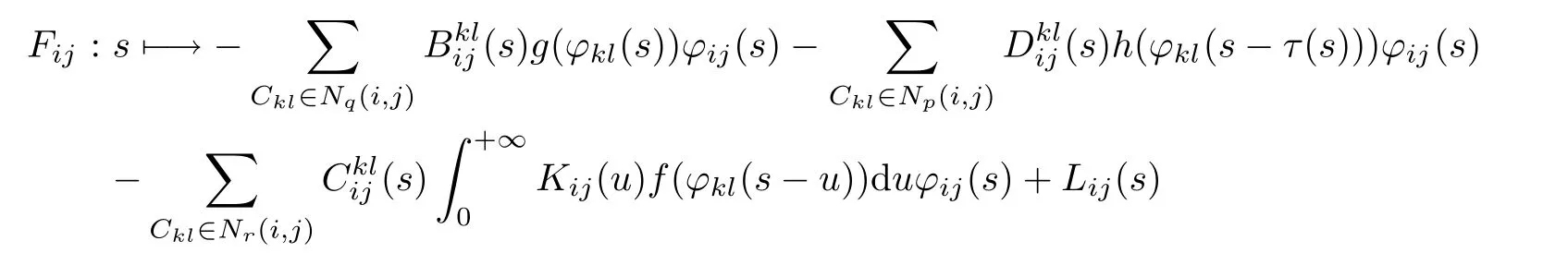
is ρ-pseudo almost-periodic,by using Lemma 4.1,Lemma 4.2,Theorem 4.3,Lemma 4.4 and the composition theorem of weighted pseudo almost-periodic functions(see[28]).Consequently,forall 1≤i≤m,1≤j≤n,Fijcan be expressed as

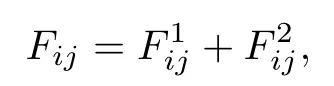
Let us prove the almost periodicity ofwe consider,in view of the almost periodicity ofa number Lǫsuch that in any interval [α,α+Lǫ]one fnds a number δ,with the property that

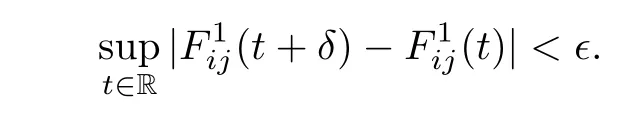
Afterwards,we can write

So,there exists θ∈]0,1[such that

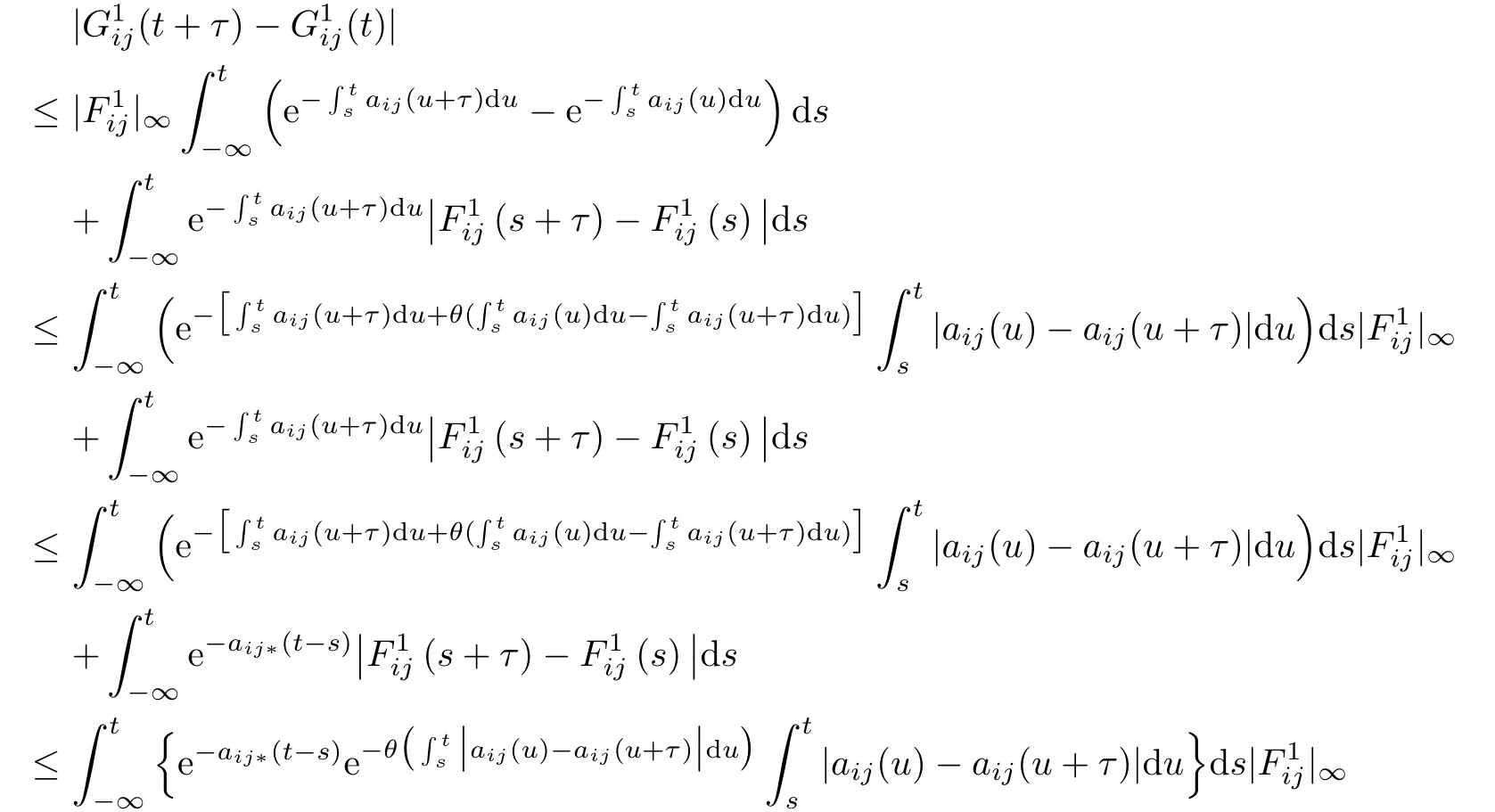
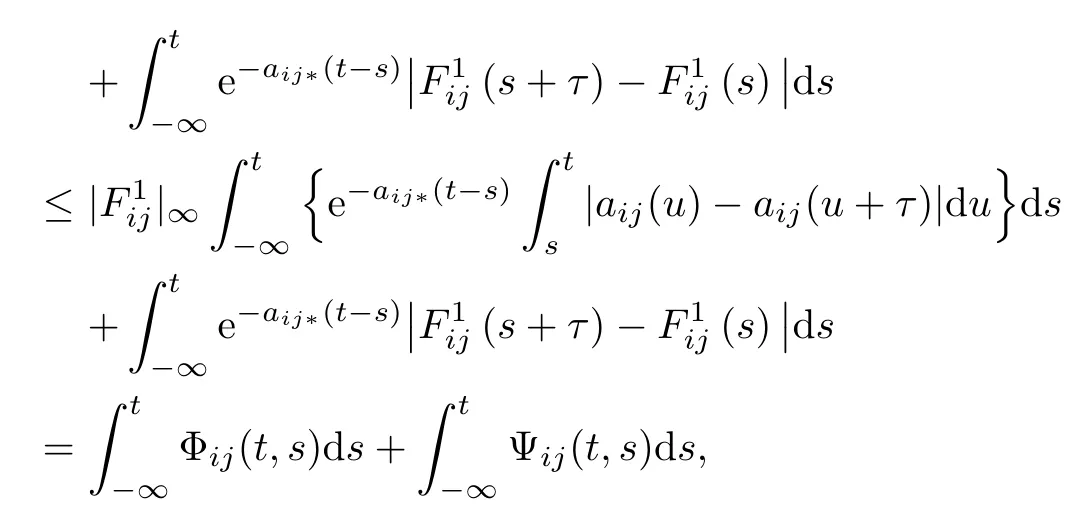
where

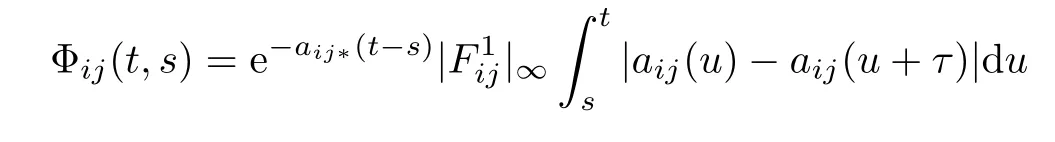
and

to prove that

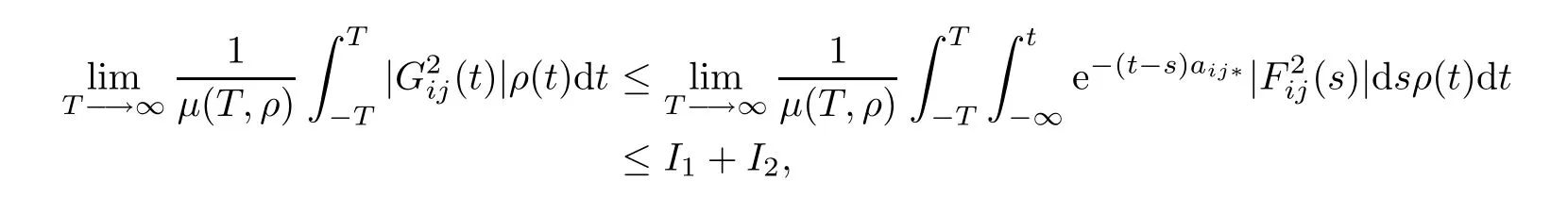
where

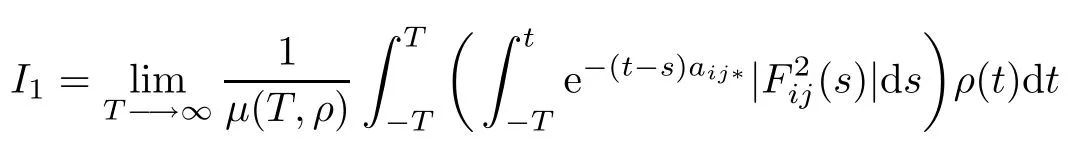
and

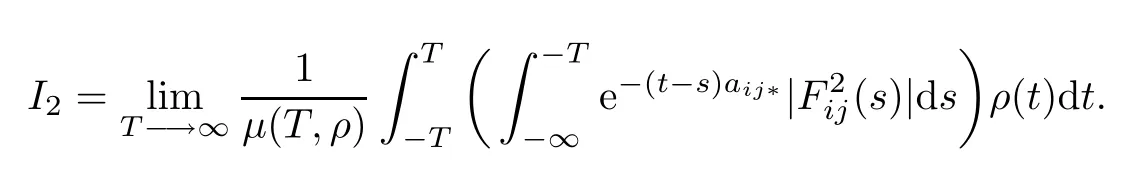
Pose m=t−s,then by Fubini’s theorem one has

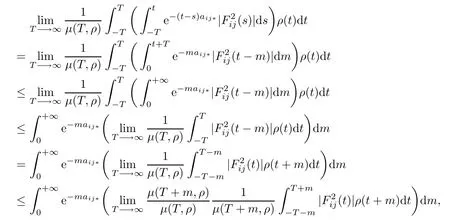
since the function F2ij(.)∈PAP0(R,R,ρ)and by the Lebesgue dominated convergence theorem, we obtain

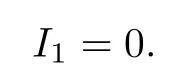
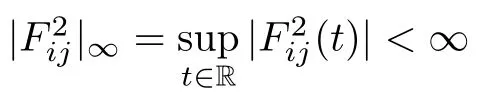
so

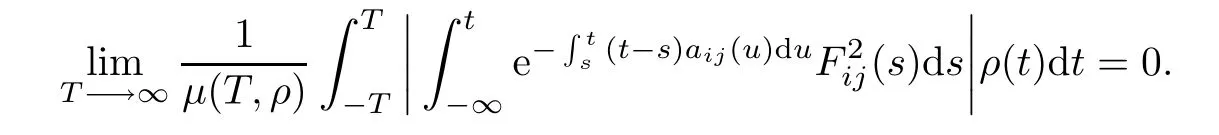
So,for all 1≤i≤m,1≤j≤n,(Γijϕ)belongs to PAP(R,R,ρ)and consequently(Γϕ) belongs to PAP(R,Rm×n,ρ).

Theorem 4.6Under conditions(H1)–(H5),and(H6).Assume that there exist nonnegative constants L,δ and q such that

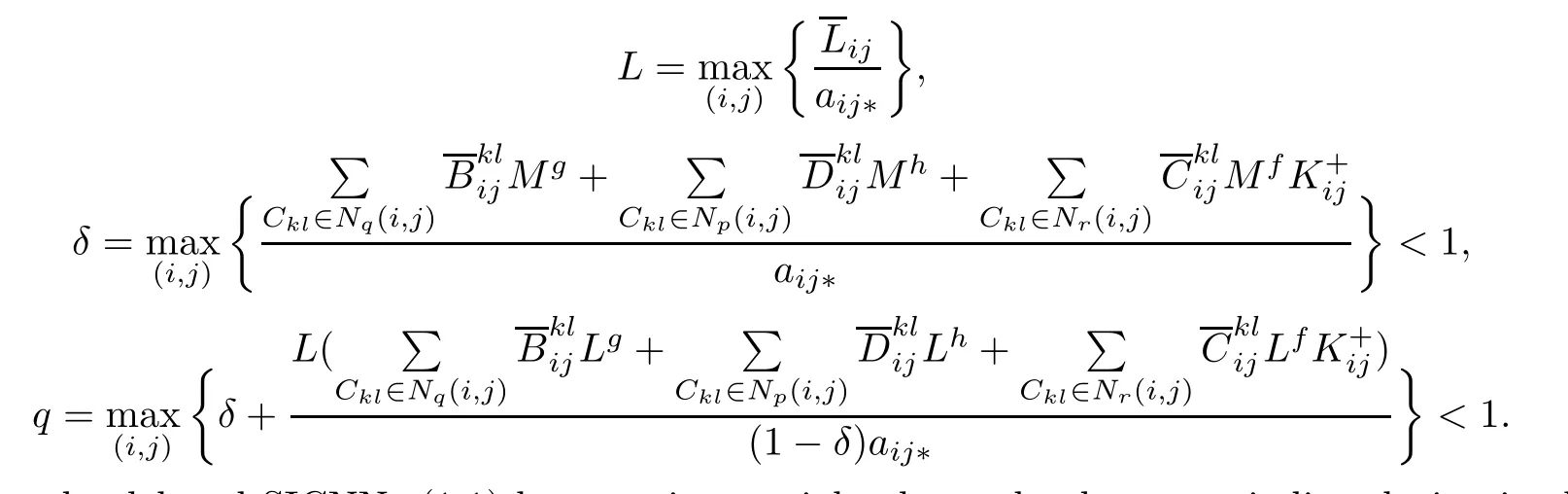
Then the delayed SICNNs(1.1)has a unique weighted pseudo almost periodic solution in the region

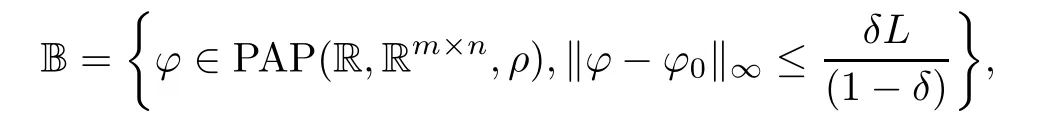
where

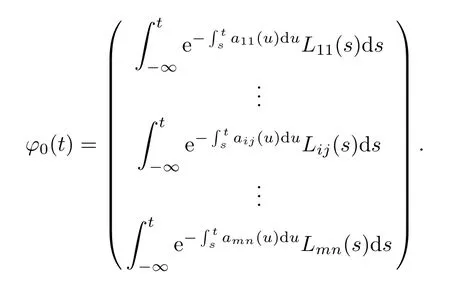
ProofOne has

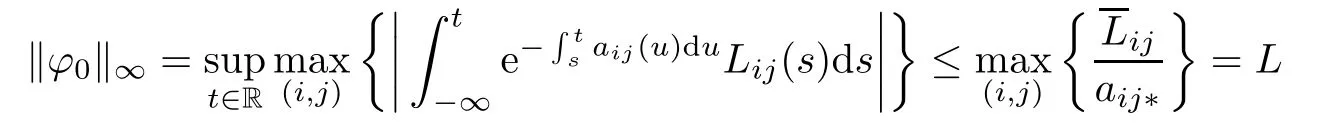
after

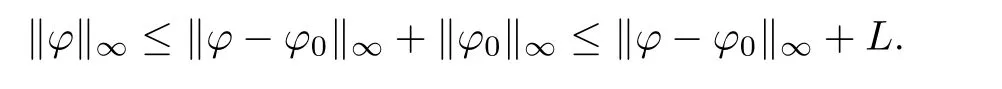
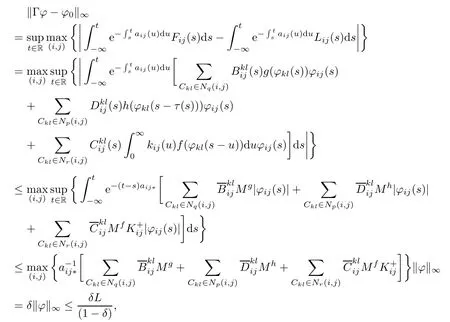
where

it implies that(Γϕ)∈B.So,the mapping Γ is a self-mapping from B to B.

Next,we prove that the mapping Γ is a contraction mapping of the B.In fact,in view of (H1),∀φ,ψ∈B,we have

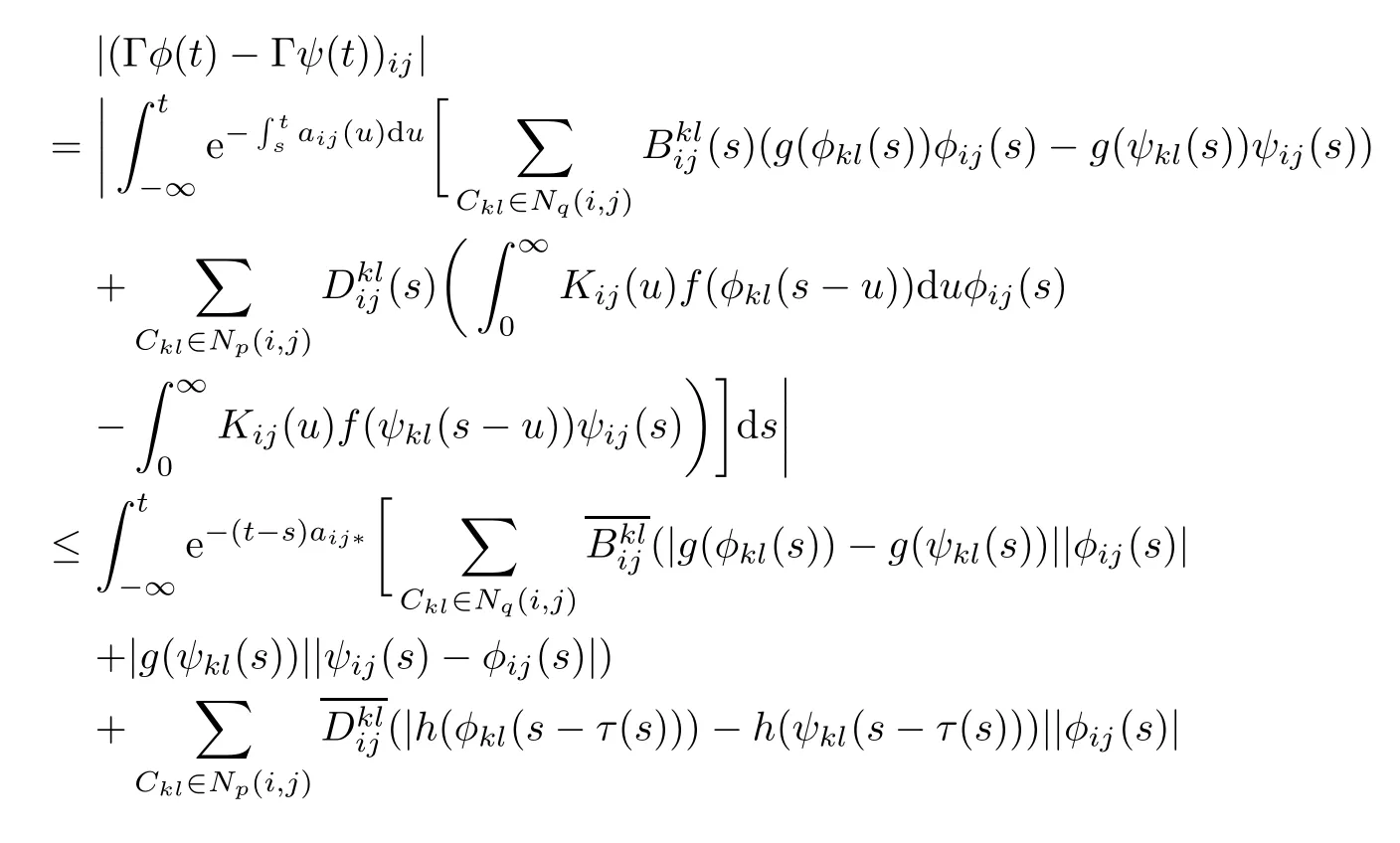
where i=1,2,···,m;j=1,2,···,n,it follows that

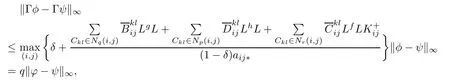
which prove that Γ is a contraction mapping.Then,by virtue of the Banach fxed point theorem, Γ has a unique fxed point which corresponds to the solution of(1.1)in B⊂PAP(R,Rm×n,ρ).

Theorem 4.7Under the conditions of Theorem 2,and if there exists a constant λ0such that

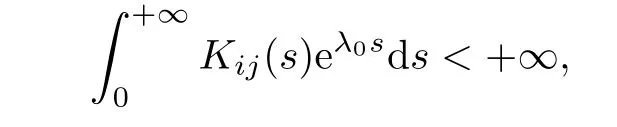
then system(1.1)has a unique weighted pseudo almost periodic solution z(t)which is globally exponentially stable.

ProofIt follows from Theorem 4.6 that system(1.1)has at least one weighted pseudo almost periodic solution z(t)=(z11(t),···,zij(t),···,zmn(t))T∈B with initial value u(t)= (u11(t),···,uij(t),···,umn(t))T.Let x(t)=(x11(t),···,xij(t),···,xmn(t))Tbe an arbitrary solution of system(1.1)with initial value

Let Gij(.)be defned by

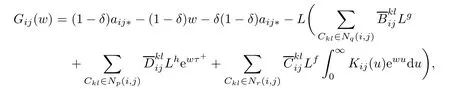
where i=1,···,m,j=1,···,n,w∈[0,+∞[and by(H2)and δ<1,we obtain that

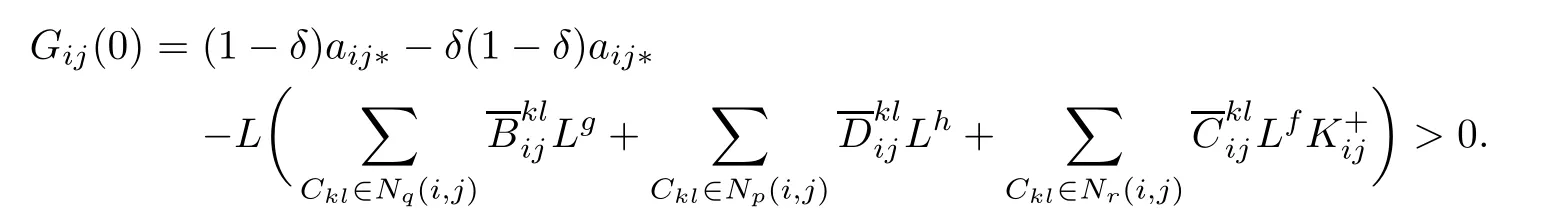
Since Gij(.)is continuo onsuch thatand

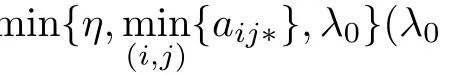
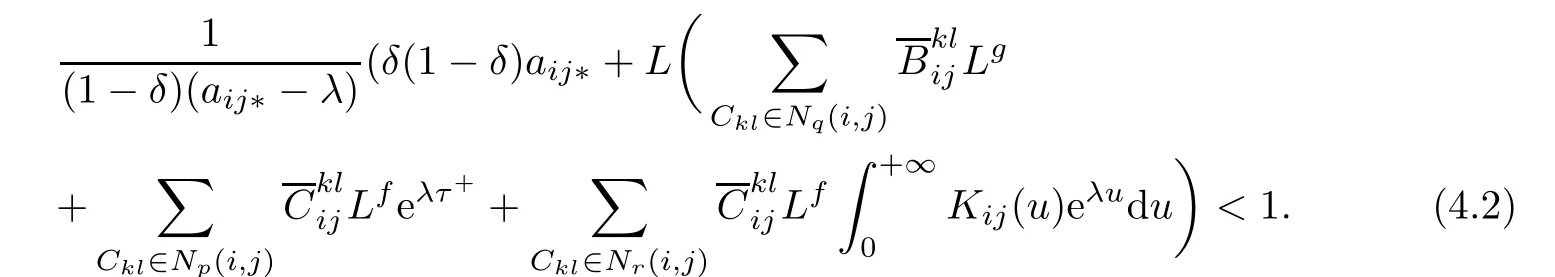
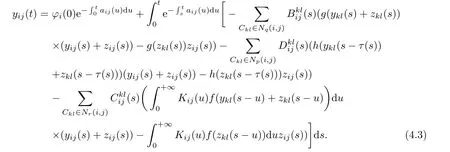
Let

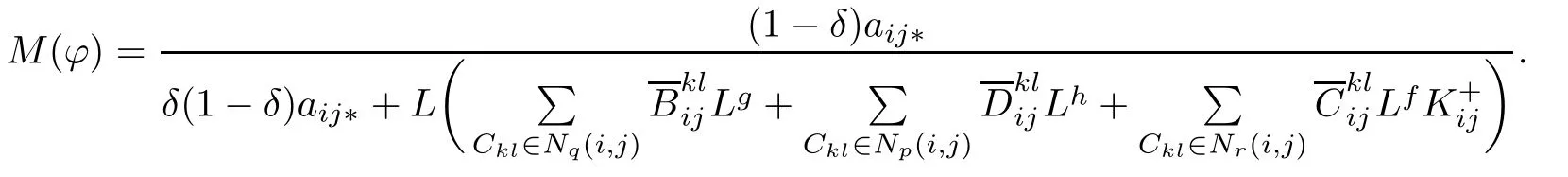
Clearly M(ϕ)>1 and

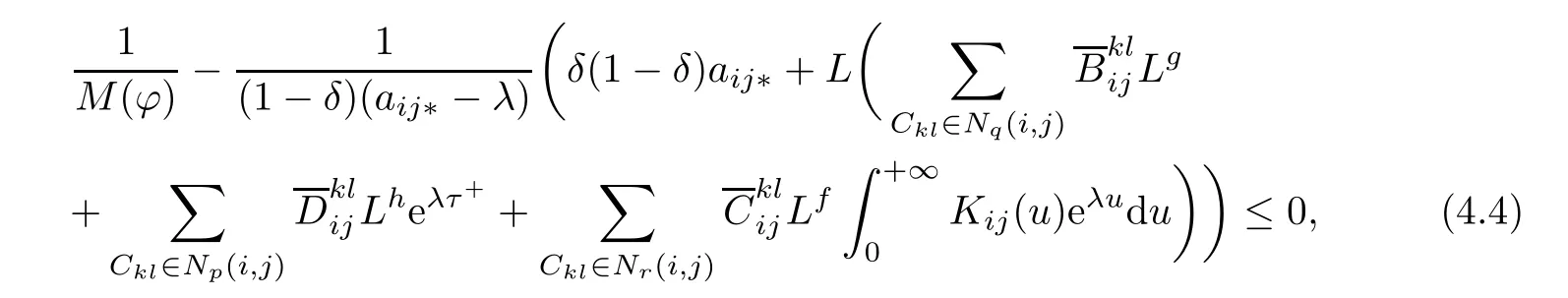
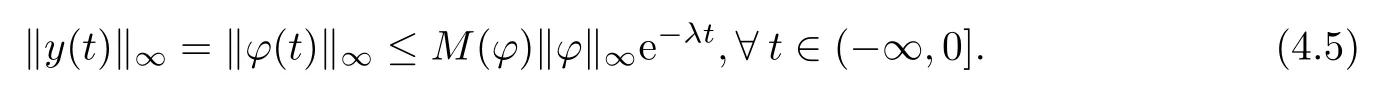
We claim that

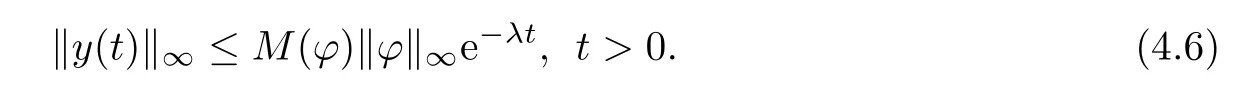
To prove(4.6),we frst show for any p>1,the following inequality holds

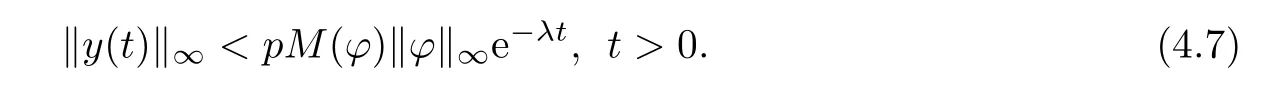
If(4.7)is false,then there must be some t1>0 and some i∈{1,···,m}and j∈{1,···,n} such that

and

By(4.2),(4.3),(4.4)and(4.9),we have

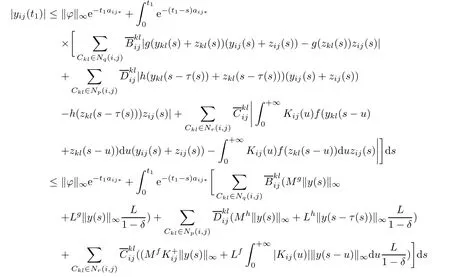
which contradicts equality(4.8)and so(4.7)holds.Letting p−→1,then(4.6)holds.Hence, the weighted pseudo almost periodic solution of system(1.1)is globally exponentially stable. The globally exponential stability implies that the weighted pseudo almost periodic solution is unique.We complete the proof.

5 Application

Let us consider the following SICNNs:

where Kij(t)=e−t⇒K+ij=1,τ(t)=12|cost|and r=q=p=1.

For all x∈R

and for ρ(t)=etlet

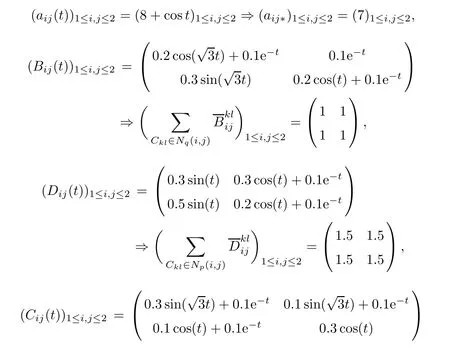
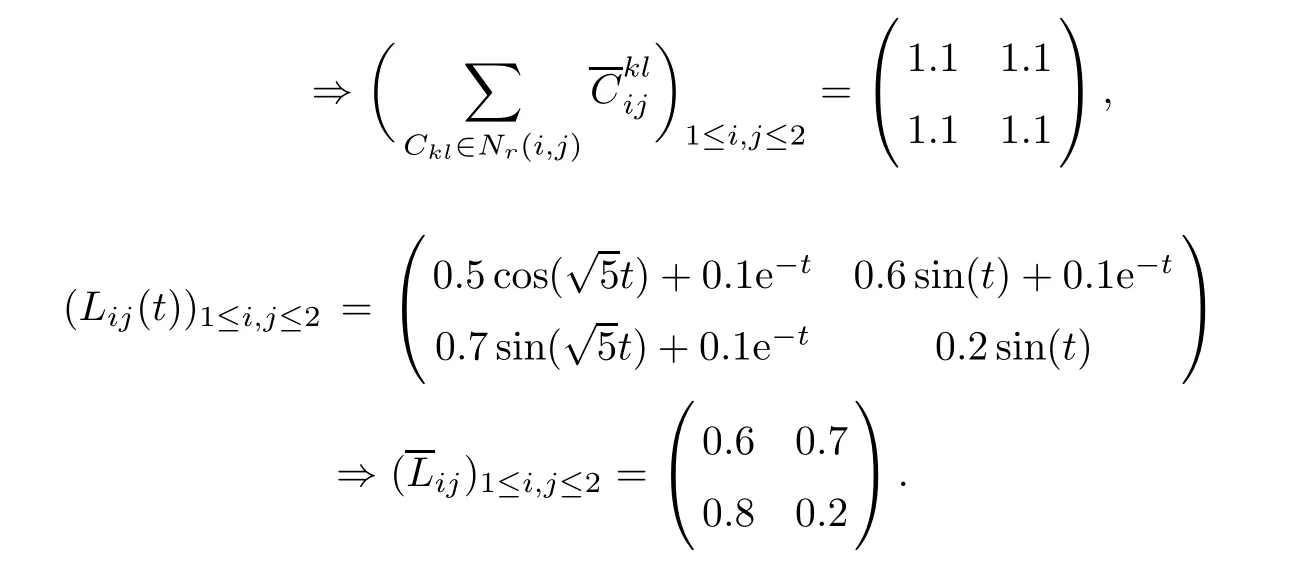
Then

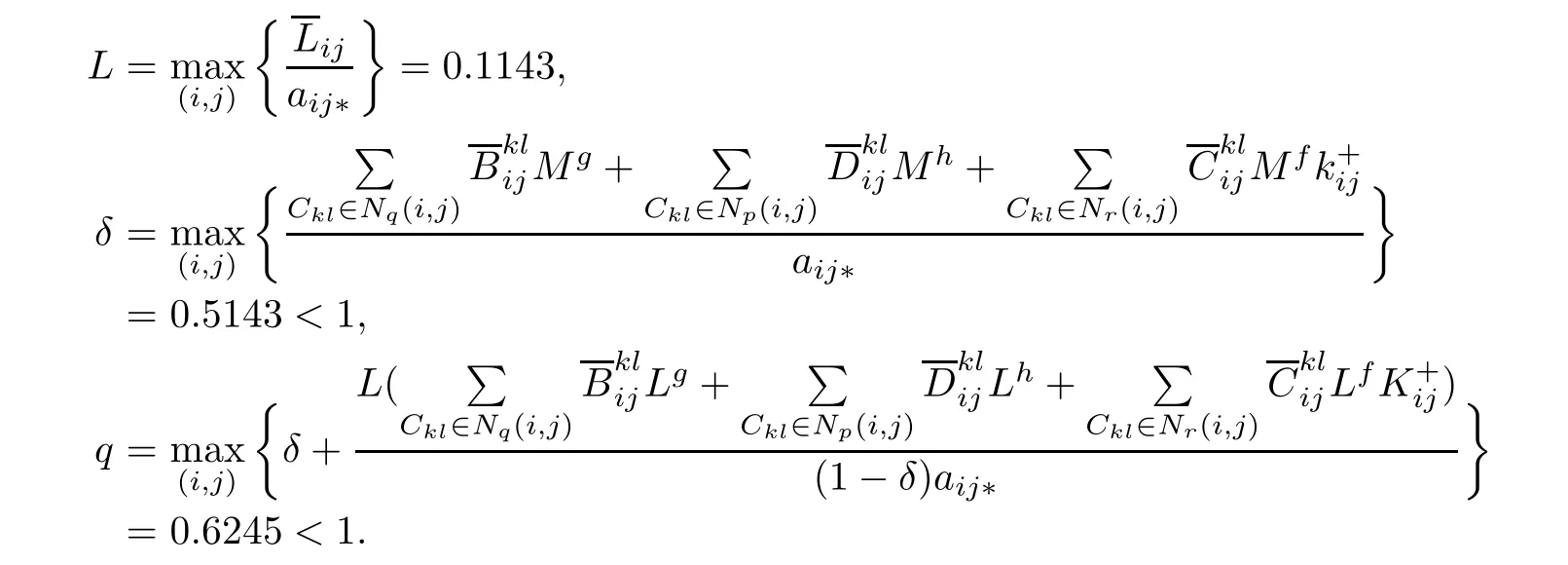
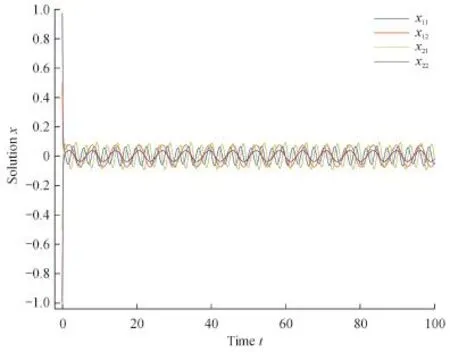
Fig.1 Curve of the weighted pseudo almost-periodic solution for SICNNs with mixed delays

And for ρ(t)=et,aij∗=7 with i,j=1,2,we haveAll conditions from Theorems 4.6,4.7 are satisfed,then the delayed SICNNs(5.1)has a unique weighted pseudo almost-periodic solution in the region

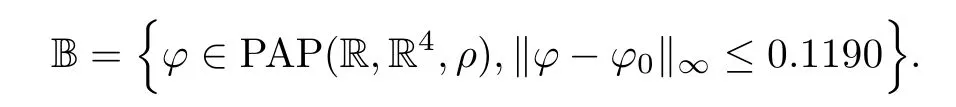
6 Conclusion

We remark that,in nature there is no phenomenon that is purely periodic,and this gives the idea to consider the almost-periodic oscillation,the pseudo almost-periodic and weighted pseudo almost-periodic situations.So,in this paper,some sufcient conditions are presented ensuring the existence and uniqueness of weighted pseudo almost-periodic solutions of shunting inhibitory cellular neural networks with mixed delays.In this work,we show that for the same assumptions in[2]plus other assumptions that we add to realize our demonstrations,allows us to show the existence and the stability of solutions of(1.1)in a weighted pseudo almostperiodic set broader than that in[2]almost periodic set.Finally,an illustrative example is given to demonstrate the efectiveness of the obtained results.

[1]Bouzerdoum A,Pinter R B.Shuatiny inhibitory collular neural networks derivation and stability analysis. IEEE Trans Circuits Sys I Fund Theory Appl,1993,40:215–221

[2]Chen Anping,Cao Jinde.Almost periodic solution of shunting inhibitory CNNs with delays.Phy Lett A, 2002,298:161–170

[3]Liu Bingwen,Huang Lihong.Almost periodic solutions for shunting inhibitory cellular neural networks with time-varying delays.Appl Math Lett,2007,20:70–74

[4]Liu Bingwen,Huang Lihong.New results of almost periodic solutions for recurrent neural networks.J Comput Appl Math,2007,206:293–305

[5]Liu Bingwen,Huang Lihong.Positive almost periodic solutions for recurrent neural networks.Nonlinear Anal:RWA,2008,9:830–841

[6]Boudour Ammar,Farouk Ch´erif,Alimi A M.Existence and uniqueness of pseudo almost-periodic solution recurrent neural networks with time varying coefcient and mixed delays.IEEE,2012,23:109–118

[7]Chaouki Aouiti,Mohammed Salah M’hamdi,Abderrahmane Touati.Pseudo almost automorphic solutions of recurrent neural networks with time-varying coefcients and mixed delays.Neural Proc Lett,DOI 10.1007/s11063-016-9515-0

[8]Bai Chuanzhi.Global stability of almost periodic solution of hopfeld neural networks with neutral timevarying delays.Appl Math Comput,2008,203:72–79

[9]Bai Chuanzhi.Existence and stability of almost periodic solutions of hopfeld neural netwokrs with continuously distributed delays.Nonlinear Anal,2009,71:5850–5859

[10]Ou Chunxia.Almost periodic solutions for shunting inhibitory cellular neural networks.Nonlinear Anal: RWA,2009,10:2652–2658

[11]Cao Jinde.A set of stability criteria for delayed cellular neural networks.IEEE Trans Circuits Syst-I,2001, 48(4):494–498

[12]Cao Jinde,Abdulaziz Alof,Abdullah Al-Mazrooei,Ahmed Elaiw.Synchronization of Switched interval networks and applications to chaotic neural networks.Abstract Appl Anal,2013,2013:Article ID 940573

[13]Cao Jinde,Chen Anping,Huang Xia.Almost periodic attractor of delayed neural networks with variable coefcients.Phy Lett A,2005,340:104–120

[14]Cao Jinde,Wan Ying.Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays.Neural Networks,2014,53:165–172

[15]Wu Haihui.Pseudo almost-periodic solution of shunting inhibitory cellular neural networks with delay.J Appl Math,2011,2011:Article ID 510789

[16]Jiang Haijun,Cao Jinde.Global exponential stability of periodic neural networks with time-varying delays. Neurocomputing,2006,70:343–350

[17]Jiang Haijun,Teng Zhidong.Global exponential stability of cellular neural networks with time-varying coefcients and delays.Neural Networks,2004,17:1415–1425

[18]Huang He,Cao Jinde,Wang Jun.Global exponential stability and periodic solutions of recurrent neural networks with delays.Phy Lett A,2002,298:393–404

[19]Xiang Hongjun,Cao Jinde.Almost periodic solutions of recurrent neural networks with continuously distributed delays.Nonlinear Anal,2009,71:6097–6108

[20]Xiang Hongjun,Cao Jinde.Almost periodic solution of Cohen-Grossberg neural networks with bounded and unbounded delays.Nonlinear Anal:RWA,2009,10:2407–2419

[21]Ding Hui-Sheng,Ye Guo-Rong.Exponential convergence of solutions of SICNNS with mixed delays.Elect J Difer Equ,2009,41:1–7

[22]Shao Jianying,Wang Lijuan,Ou Chunxia.Almost periodic solutions for shunting inhibitory cellular neural networks without global Lipschitz activaty functions.Appl Math Model,2009,33:2575–2581

[23]Chua L O,Yang L.Cellular neural networks:application IEEE Trans Circuits Sys,1988,35(10):1273–1290

[24]Chen Ling,Zhao Hongyong.Global stability of almost periodic solution of shunting inhibitory cellular neural networks with variable coefcients.Chaos,Solitons and Fractals,2008,35:351–357

[25]Fan Qiyi,Shao Jianying.Positive almost periodic solutions for shunting inhibitory cellular neural networks with time-varying and continuously distributed delays.Commun Nonlinear Sci Numer Simulat,2010,15: 1655–1663

[26]Syed Abbas,Lakshman Mahto,Mokhtar Hafayed,Alimi A M.Asymptotic almost automorphic solutions of impulsive neural network with almost automorphic coefcients.Neurocomputing,2014,142(22):326–334 [27]Roska T,Chua L O.Cellular neural networks with non-linear and delay-type template elements and nonuniform grids.International J Circuit Theory Appl,1992,20:469–481

[28]Diagana Toka.Weighted almost periodic functions and applications.Comptes Rendus Acadmie des Sciences Paris Ser I,2006,343:643–646

[29]Diagana Toka.Weighted pseudo almost periodic solution to some diferentiable equations.Nonlinear Anal, 2008,68:2250–2260

[30]Diagana Toka.Weighted pseudo almost periodic solution to a neutral delay integral equation of advanced type.Nonlinear Anal,2009,70:298–304

[31]Wang Wentao,Liu Bingwen.Global exponential stability of pseudo almost periodic solutions for SICNNs with time-varying leakage delays.Appl Anal,2014,2014:Article ID 967328

[32]Chen Xiaoxing,Hu Xiangyang.Weighted pseudo almost periodic solutions of neutral functional dif´erentielle equations.Nonlinear Anal:RWA,2011,12:601–610

[33]Yang Xinsong,Cao Jinde,Huang Chuangxia,Yao Long.Existence and global exponential stability of almost periodic solutions for SICNNs with nonlinear behaved functions and mixed delays.Abst Appl Anal,2010, 2010:Article ID 915451

[34]Lin Yiguang,You Zhisheng,Cao Liping.On the almost periodic solution of generalized shunting inhibitory cellular neural networks with continuously distributed delays.Phy Lett A,2006,360:122–130

[35]Lin Yiguang,You Zhisheng,Cao Liping.Almost periodic solution of shunting inhibitory cellular neural networks with time varying and continuously distributed delays.Phy Lett A,2007,364:17–28

[36]Li Yongkun,Wang Chao.Almost periodic functions on time scales and applications.Discr Dyn Nature Soc, 2011,2011:Article ID 727068

[37]Wu Yuanyuan,Cao Jinde,Abdulaziz Alof,et al.Finite-time boundedness and stabilization of uncertain switched neural networks with time-varying delay.Neural Networks,2015,69:135–143

[38]Lin Zhensheng,Lin Yan-Xin.Linear Systems Exponential Dichotomy and Structure of Sets of Hyperbolic Points.Singappore:World Scientifc Pub Co,2000

∗Received June 10,2015;revised January 26,2016.