基于用户相似度加权的Slope One算法
摘要:SlopeOne算法基于简单的线性回归模型,通过减少响应时间和维护难度,显著提高了推荐性能。然而SlopeOne算法没有考虑用户内部的关联,同等地使用各个用户数据进行预测,容易造成偏差,影响推荐质量。本文提出了一种改进的Slope One算法,它将用户相似度纳入考虑并且对评分偏差计算公式进行了修正。基于项目的Slope One算法结合基于用户的协同过滤算法,提出新的混合推荐算法US-Slope One。在MovieLens数据集上的实验结果表明,该算法与原Slope One算法相比具有更好的预测准确度和推荐质量。
关键词:协同过滤;用户相似度;SlopeOne;数据挖掘;个性化推荐
中图分类号:TP391 文献标识码:A DOI:10.3969/j.issn.1003-6970.2016.04.015
0 引言
当今互联网信息量不断扩大,网络经济发展迅猛,信息过载成为社会性问题。个性化推荐系统是解决这一问题的一种有效工具。协同过滤技术在推荐系统,尤其是在电子商务中得到了广泛的应用,几乎所有大型电子商务平台都使用了各种推荐系统,对用户的特征和喜好进行分析,并提供更具个性化的推荐。协同过滤利用具有相似经验的用户群体的偏好信息为特定用户进行商品或信息的推荐。根据模型的不同,协同过滤可分为基于用户的协同过滤和基于项目的协同过滤。
Slope One算法是一种基于项目的协同过滤算法,它使用一个线性回归模型进行预测,在与其他复杂的协同过滤推荐具有同等推荐精度的前提下,花销更少,更加易于实现。它的简洁高效使得采用Slope One算法的推荐系统更加易于实现和维护。然而,Slope One算法在进行推荐时,没有考虑到用户的作用,用户间的内在关联对预测结果起着重要影响。Slope One算法不加区分地采用所有用户评分数据来计算项目之间的偏差,这就导致一些与当前活跃用户偏好不同甚至相反的用户数据同等参与了预测,这会削弱拥有高相似度的用户的作用效果,使得预测精度降低。采用聚类或动态k近邻可以去除部分噪声数据,但却造成了数据丢失。数据稀疏性问题是当前推荐系统所面临的主要问题之一。在数据极端稀疏的情况下,数据的缺失将使得推荐效果很不理想。
因此本文提出了一种改进的Slope One算法(US-Slope One),利用用户相似度对用户评分差值进行加权,使得拥有不同相似度的用户数据以不同权重参与预测,实现在尽可能保证不丢失评分信息的前提下,在非稠密数据集中的推荐精度得到提升。
1 Slope one算法理论
1.1 SlopeOne算法
假设推荐系统中有m个用户和n个项目,分别建立两个集合U={u1,u2,…,um}和I={i1,i2,…,in},U代表用户集合,I代表项目集合。推荐算法常用矩阵Rm×n来表示不同用户对每个项目的评分。行向量Rm表示每个用户的评分,列向量Rn表示每个项目的得分。为了使计算更加明确,采用ri,j(1≤i≤m,1≤j≤n)表示用户i对项目j的评分。
SlopeOne算法采用f(x)=x+b进行预测,其中参数6是用户对两项目的平均评分偏差。Slope One算法先计算项目ii与其他项目ik之间的平均评分偏差devjk,再预测当前活跃用户u对目标项目,的可能评分Predictionu,j。定义Sjk为给项目ij和项目ik都评过分的用户集合,Rj为与项目ij同时被评分的项目集合,count(X)为集合X中的元素个数。SlopeOne算法如下:
(1)
(2)
1.2 加权Slope One算法
为平衡每个项目对目标项目的影响,同时对项目ij和ik评过分的用户数目sjk将作为权重加入两项目评分偏差的计算,其中sjk=count(Sjk)。
(3)
1.3 双极Slope One算法
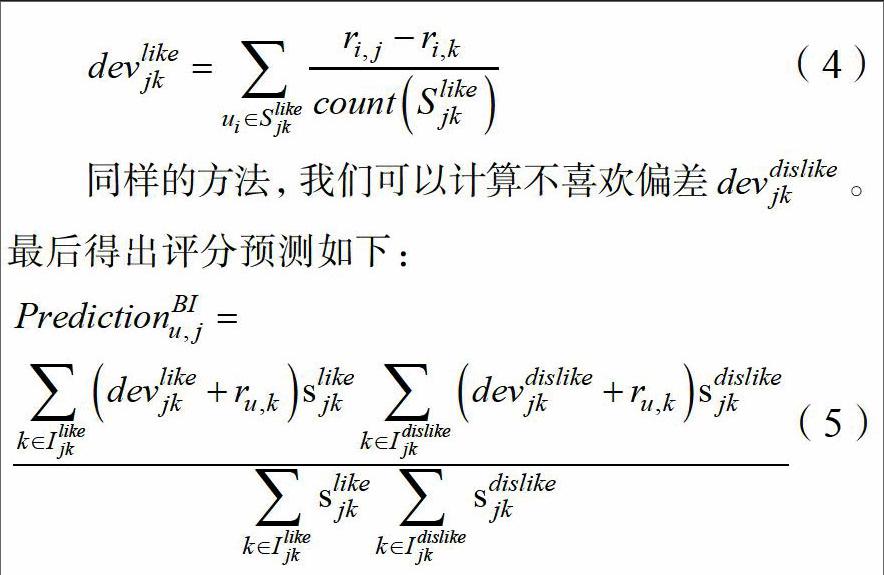
双极Slope One算法考虑到用户对物品的喜好,将项目集合Ijk府划分为两部分,一个是用户评分高于其评分均值的项目集合Ilikejk,剩下的构成Idislikejk。从而分别计算出喜欢偏差devlikejk和不喜欢偏差devdislikejk。
(4)
同样的方法,我们可以计算不喜欢偏差devdislikejk。最后得出评分预测如下:
(5)
2 US-Slope one算法设计
如前一章所述,Slope One算法采用所有用户评分数据而不考虑相似度问题,当存在大量噪声数据时,预测准确度会大大降低,导致最终的推荐结果不理想。然而在数据极度稀疏的情况下,往往又希望保留尽可能多的数据,US-Slope One算法针对这一问题,采用用户相似度进行加权,使得相似度不同的用户数据以不同权重加入预测。常用的用户相似性度量方法有余弦相似性,修正余弦相似性,皮尔逊相关系数以及斯皮尔曼相似性等。考虑到不同用户的评分尺度问题,本文采用修正余弦相似性计算用户间相似度。若用户ua和ub的共同评分的项目集合为Iab,用户ua和ub对项目ic的评分分别为rac和rbc,ra和rb分别表示用户ua和ub的评分均值,则用户ua和ub之间的相似度sim(ua,ub)为:
(6)
将用户相似度作为评分偏差计算的权值,US-Slope One算法如下:
(7)
3 实验结果及分析
3.1 实验所用数据集
本实验所用的数据集是由GroupLens研究产品组田松瑞:基于用户相似度加权的Slope One算法提供的电影评分数据集Movielens(http://movielens.umn.edu),该数据包括943个用户对1682部电影的共计100000条评分记录,其中每位用户至少对20部电影进行了评分。评分值范围是1到5分,分值越高代表用户对电影的评价越好。该数据稀疏度为6.30%。实验时从该数据集中按一定规则随机抽取80%的数据作为训练集,其余20%作为测试集。
3.2 度量标准
用于推荐系统的推荐质量评价的度量标准主要包括统计精度度量方法和决策支持精度度量方法两种。其中统计精度度量方法的平均绝对误差MAE(Means AbsoIute Error)和均方根误差RMSE(RootMean Square Error)由于更易于理解并且能够更直观地对推荐质量进行度量,因此成为推荐质量评价最常用的方法。MAE和RMSE的值越小,代表推荐质量越高。本文实验采用MAE和RMSE作为推荐质量的度量标准。
假设两个分组P和Q分别代表预测评分集合和实际评分集合,P={p1,P2,…,pN},Q={q1,q2,…,qN}。MAE和RMSE的定义如下:
(8)
(9)
3.3 实验结果
本实验将US-slope One算法与基本Slope One算法和加权slope One算法以及双极Slope One算法进行比较,得到的MAE值和RMsE值分别如图1和图2所示。经统计学分析,实验结果具有代表性。
实验结果表明,在稀疏数据集上,US-slope One算法的MAE值和RMsE值均明显低于Slope One算法、加权Slope One算法和双极Slope One算法,其推荐精度更高。US-Slope One算法总体推荐性能更好,使用用户相似度进行加权能够在保证数据量尽可能完整的基础上显著提高了预测精度。
4 结论
本文分析了Slope One推荐算法及其改进算法,针对其在数据稀疏情况下利用有限用户评分数据做出更合理的推荐问题,提出了将用户相似度作为权重融入预测的US-Slope One算法,在尽可能保证不丢失原始数据的基础上,更加合理地运用数据。最后,对本算法以及已有算法在稀疏数据集上进行试验,比较结果表明本算法提升了现有算法对于稀疏数据集的适应性,提高了预测精度和推荐性能。