半刚性钢框架稳定理论的扣件式钢管满堂支撑体系极限承载力分析

庄明智，方圣恩

(福州大学土木工程学院，福建 福州 350116)

半刚性钢框架稳定理论的扣件式钢管满堂支撑体系极限承载力分析

庄明智，方圣恩

(福州大学土木工程学院，福建 福州 350116)

在考虑直角扣件半刚性以及材料、几何非线性等因素的情况下，对两个扣件式钢管满堂支撑体系模型(无剪刀撑S1模型、有剪刀撑S2模型)进行非线性屈曲分析，得到体系竖向荷载-位移曲线，确定了体系极限承载力.采用半刚性钢框架稳定理论，对无剪刀撑S1模型承载力进行计算.将所得结果与数值结果对比，验证了半刚性钢框架稳定理论在计算体系承载力的可行性.对直角扣件的转动性能进行试验，得到弯矩-转角曲线.采用ANSYS中的COMBIN39弹簧单元对直角扣件的转动进行模拟.

扣件式钢管满堂支撑体系；非线性屈曲分析；半钢性钢框架稳定理论；弯矩-转角曲线

0 引言

在土木工程施工过程中，扣件式钢管满堂支撑体系作为一种主要的施工临时承重结构，其安全性引起了业界的广泛重视.近年来，扣件式钢管满堂支撑体系的倒塌事故频繁发生，造成了大量人员伤亡和财产损失，通过对大量事故原因进行收集整理后发现，造成倒塌的主要原因可归为以下三点：1) 对体系的受力性能认识不清，搭设作业多凭借工人经验，未经过设计；2) 虽然经过设计，但搭设过程并没有按照规范要求进行，且建造过程中缺乏有效的检查方法和严格的监督措施；3) 由于人为操作不当或自然灾害等偶然因素造成的倒塌.

目前，针对扣件式钢管满堂支撑体系的受力性能，国内外已开展了一定的研究工作[1-4]，在试验的基础上，我国于2011年颁布了新的《建筑施工扣件式钢管脚手架安全技术规范(JGJ 130-2011)》[5](以下简

称规范(JGJ 130-2011))，其对原有旧规范进行了修改，包括增加了满堂支撑体系的计算，并对计算长度系数做了调整.但是，新规范对于扣件式钢管满堂支撑体系的计算本质上仍是基于计算长度系数的单杆稳定问题，其是对整体模型的一种简化计算，这与实际情况有较大差距.因此，对扣件式钢管满堂支撑体系受力性能的研究，整体模型的分析仍是一种精确而有效的方法[6].

首先, 简要介绍结构稳定分析的一些基本概念，在此基础上，参数化建立两个扣件式钢管满堂支撑体系数值模型(无剪刀撑模型S1，有剪刀撑模型S2), 在考虑扣件半刚性性质及初始几何缺陷的情况下，对模型进行线性和非线性屈曲分析以得到其极限承载力.其次，区别于传统的脚手架单杆稳定计算方法，借鉴半刚性钢框架稳定理论[7]，对无剪刀撑情况的简化模型进行理论计算，并将理论结果与数值分析结果及规范进行对比，以验证半刚性钢框架稳定理论在计算满堂支撑体系承载力上的有效性.最后，根据试验所得扣件转动刚度参数，采用有限元软件对其转动特征进行模拟.

1 扣件式钢管满堂支撑体系屈曲分析

1.1 屈曲分析理论

屈曲分析[8-9]是一种用于确定结构开始变得不稳定时的临界荷载和屈曲模态形状的技术.屈曲分析包括线性屈曲分析和非线性屈曲分析.在对结构进行屈曲分析时，通常先进行线性屈曲分析，以确定结构最容易失稳的屈曲模态及临界荷载上限值，在此基础上，考虑几何、材料的非线性性质，对结构进行非线性屈曲分析，以获得更为近似的临界荷载.

线性屈曲分析用于预测一个理想弹性结构的理论屈曲强度，其求解方法如下：

在线弹性状态下荷载-位移关系为：

假设位移很小，任意状态下({P}, {ψ}, {σ})增量平衡方程为：

其中：{ψ0}为荷载{P0}对应的位移; [Ke]为弹性刚度矩阵; {σ}为应力; [Kσ(σ)]为应力状态{σ}下的初始应力矩阵.

假设加载过程为线性函数：

则增量平衡方程可写为：

当达到临界荷载时，{ΔP}趋于零，而位移{Δψ}仍在增加，此时增量平衡方程为：

以上方程若要成立，则必须满足：

求解上式得到的λ即为临界荷载的特征值，而Pcr=λ×P0即为临界荷载，其中P0可取为单位荷载.

非线性屈曲分析由于考虑了结构初始缺陷及材料非线性等因素，其分析结果比线性屈曲分析更为精确，因此在实际工程应用中，多采用非线性屈曲分析.在分析过程中，首先将线性屈曲分析得到的一阶屈曲模态以一定比例作为初始几何缺陷来更新原模型，此后，逐级增加荷载进行非线性静力分析以求得结构开始变得不稳定的临界荷载.在每一级荷载求解之后，进入下一级荷载求解之前，程序将自动调整刚度矩阵以反映非线性变化.

1.2 模型分析

由于目前倒塌案例多为高大模板，如学校、商场等内天井支撑、高架桥桥面支撑等，因此，将分析模型高度取为8 m，考虑到求解成本的原因，跨数只取5跨×5跨.同时, 根据是否设置剪刀撑，将模型分为S1、S2(图1)，利用有限元软件建立扣件式钢管满堂支撑体系模型，模型X向与Y向跨度均为4.5 m，立杆间距0.9 m，步距1.5 m，架体高度8 m，顶部立杆伸出水平杆长度0.3 m，脚手架钢管采用标准48.3×3.6钢管(BEAM188单元模拟)，弹性模量2.06×105MPa，屈服强度205 MPa，杆件间采用直角扣件连接(COMBIN14单元模拟，转动刚度来源于文[6], 取为19 kN·m·rad-1)，立杆底部与地面假设为铰接，荷载以集中力形式施加于顶部.此外，模型中还考虑了地面及顶部方木、顶托、模板等构件对架体整体受力性能的影响.

对这两种满堂支撑体系进行线性屈曲分析，屈曲模态如图2.从临界荷载来看，S1模型的结果为12.599 kN，而S2的结果为32.413 kN，说明设置剪刀撑是提高承载力和稳定性的一种极为有效的方式，在实际工程中，满堂支撑体系都设置有剪刀撑.此外，在不考虑上部模板、方木等构件的情况下，对S1模型进行承载力分析，其计算结果为11.833 kN，与考虑了模板、方木的情况相比，其承载力略有下降.其原因是：外侧立杆与内侧立杆相比，其所受约束较少，因此在相同荷载作用下更容易失稳，而方木、模板等上部结构的存在，恰好起到了拉结作用，约束了各立杆的单独侧向变形，提高了架体的整体性，承载力略有提高.在分析中，不考虑顶部结构的分析结果更为保守，故计算分析中可不考虑顶部结构的有利影响.

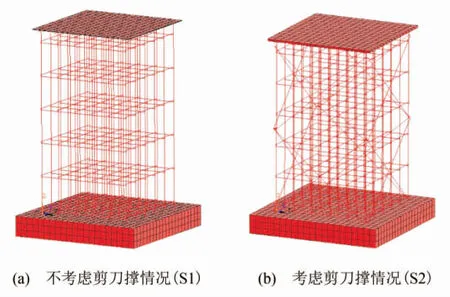
图1 数值分析模型Fig.1 Numerical analysis model

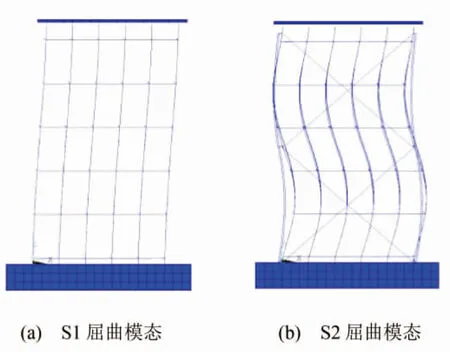
图2 S1和S2屈曲模态Fig.2 Bucking modes of S1and S2

对结构进行非线性屈曲分析，将《规范(JGJ 130-2011)》[5]中关于立杆垂直度要求和钢管初弯曲允许值与一阶模态中对应的最大位移的比值，作为初始几何缺陷更新模型，再通过逐级加载的方式得到极限荷载.以下是两种模型的非线性分析荷载-位移曲线(图3)，其中S1的分析结果为11.680 kN，而S2的分析结果为20.140 kN.由于考虑了几何、材料等的非线性特征，此分析结果更为接近真实情况.

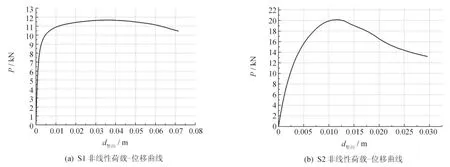
图3 非线性分析荷载-位移曲线Fig.3 Load-displacement curves of nonlinear analysis

2 基于半刚性钢框架稳定理论的扣件式钢管满堂支撑体系极限承载力计算

2.1 规范公式

在《规范(JGJ 130-2011)》[5]中给出了扣件式钢管满堂支撑体系的稳定承载力的计算方法，根据是否考虑风荷载的情况，分别给出了以下两种计算公式：

不考虑风荷载:

考虑风荷载:

其中：N为计算立杆段的轴向力设计值; φ为轴心受压构件稳定系数; A为截面面积; Mw为风荷载产生的弯矩设计值; W为截面模量; f为钢材抗弯强度设计值.

根据以上公式，在不考虑风荷载的情况下，分别对以上S1和S2模型进行计算，计算结果显示，S1的极限承载力为15.871 kN，而S2的极限承载力为19.501 kN.该计算公式是将满堂支撑体系的稳定问题简化为单杆稳定问题，通过立杆计算长度转化得到的稳定系数来考虑扣件半钢性对承载力的影响，其并没有考虑立杆间相互作用的影响，这与实际情况并不相符.因此，与数值分析结果相比可以发现，S1的计算结果相差较大，达到35.88%，而S2的相差结果为3.17%.为了得到更为准确的理论计算结果，借鉴现有的半刚性钢框架稳定分析理论，在一定合理假设下，对扣件式钢管满堂支撑体系进行理论计算.

2.2 半刚性钢框架稳定理论计算

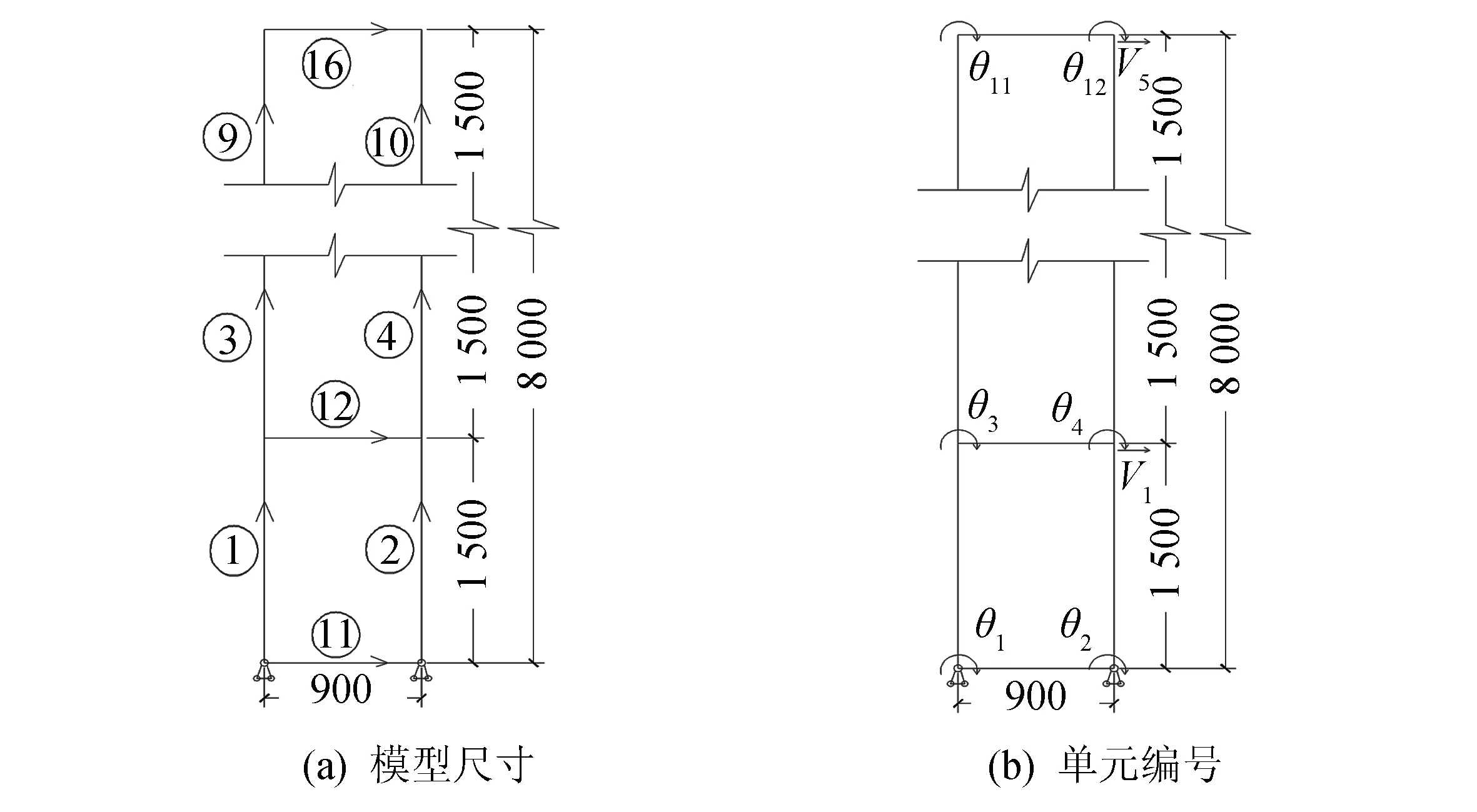
图4 计算简图 (单位：mm )Fig.4 Calculation diagram (unit：mm )

对无剪刀撑情况S1进行简化计算，不考虑架体上部结构的影响，只对满堂支撑体系本身进行研究.通过整体模型与平面单跨模型线性屈曲分析, 结果发现，当顶部各立杆在相同荷载作用下，二者结果十分接近，因此可以将平面单跨模型作为理论计算模型，计算简图如图4.

借鉴半刚性钢框架稳定分析理论[7, 10-11]，建立考虑连接节点柔性的半刚性横杆单元和考虑几何非线性影响的立杆单元，再利用有限单元法求解扣件式钢管满堂支撑体系的临界荷载.

考虑节点柔性的半刚性横杆单元刚度矩阵为:

式中:

RkA为直角扣件转动刚度，由于RkA=RkB=19 kN·m·rad-1，所以rii=rjj，因此:

考虑几何非线性影响的立杆单元刚度矩阵为:

求解扣件式钢管满堂支撑体系临界荷载.

将单元在局部坐标系下的刚度矩阵通过坐标变换转化为整体坐标系下的刚度矩阵，再进行刚度矩阵组装，形成整体刚度矩阵，则可得到如下方程：

根据上述方法，得到的理论计算结果为临界荷载P=11.967 kN，而数值分析结果为临界荷载P=11.833 kN，二者相差结果仅为1.13%，现将数值、规范、半刚性钢框架稳定理论三者所得的结果及差值列于表1.

表1 不同分析方法承载力对比结果及差值Tab.1 Load capacity results and differencesof different analysis method

从表1可以看出，将半刚性钢框架稳定理论用于计算扣件式钢管满堂支撑体系的稳定承载力是可行的，且计算精度较高.但是，由于采用半刚性钢框架稳定理论计算扣件式钢管满堂支撑体系承载力时，并没有考虑搭设剪刀撑的情况，而实际情况下应当设置剪刀撑，因此，在实际工程应用中，可以将剪刀撑作为一种安全储备，而采用半钢性钢框架理论计算的结果相对保守.

3 扣件转动非线性数值模拟

3.1 扣件转动刚度试验

为了更好地模拟直角扣件的转动，对直角扣件进行转动刚度试验，以得到反映转动刚度的弯矩-转角曲线.试验构件及装置如图5所示，将2 m的横杆与1 m的立杆通过直角扣件连接，在横杆一端施加竖向集中力，在立杆、横杆各距扣件中心200 mm 处各布置一个位移计.加载过程中，0～0.06 kN荷载步取为0.02 kN，0.08～0.3 kN荷载步取为0.04 kN，最后, 0.3～0.9 kN荷载步取为0.1 kN.记录每一荷载步下位移计的读数，通过三角函数转化后得到对应的弯矩-转角曲线.

图5 扣件转动刚度试验Fig.5 Rotation stiffness test of coupler

3.2 扣件转动刚度数值模拟

在得到直角扣件转动的弯矩-转角曲线后，就可利用ANSYS有限元软件中的COMBIN39非线性弹簧单元来模拟直角扣件的转动特性.模拟结果如图6所示，提取相应位置的节点位移，同样通过三角函数转化后，得到弯矩-转角曲线(图7)，对比试验与数值分析得到的曲线可以看出，试验曲线与数值曲线几乎重合，说明COMBIN39非线性弹簧单元可以很好地模拟直角扣件的转动特征，这对进一步进行整体承载力屈曲分析具有实质性的意义.

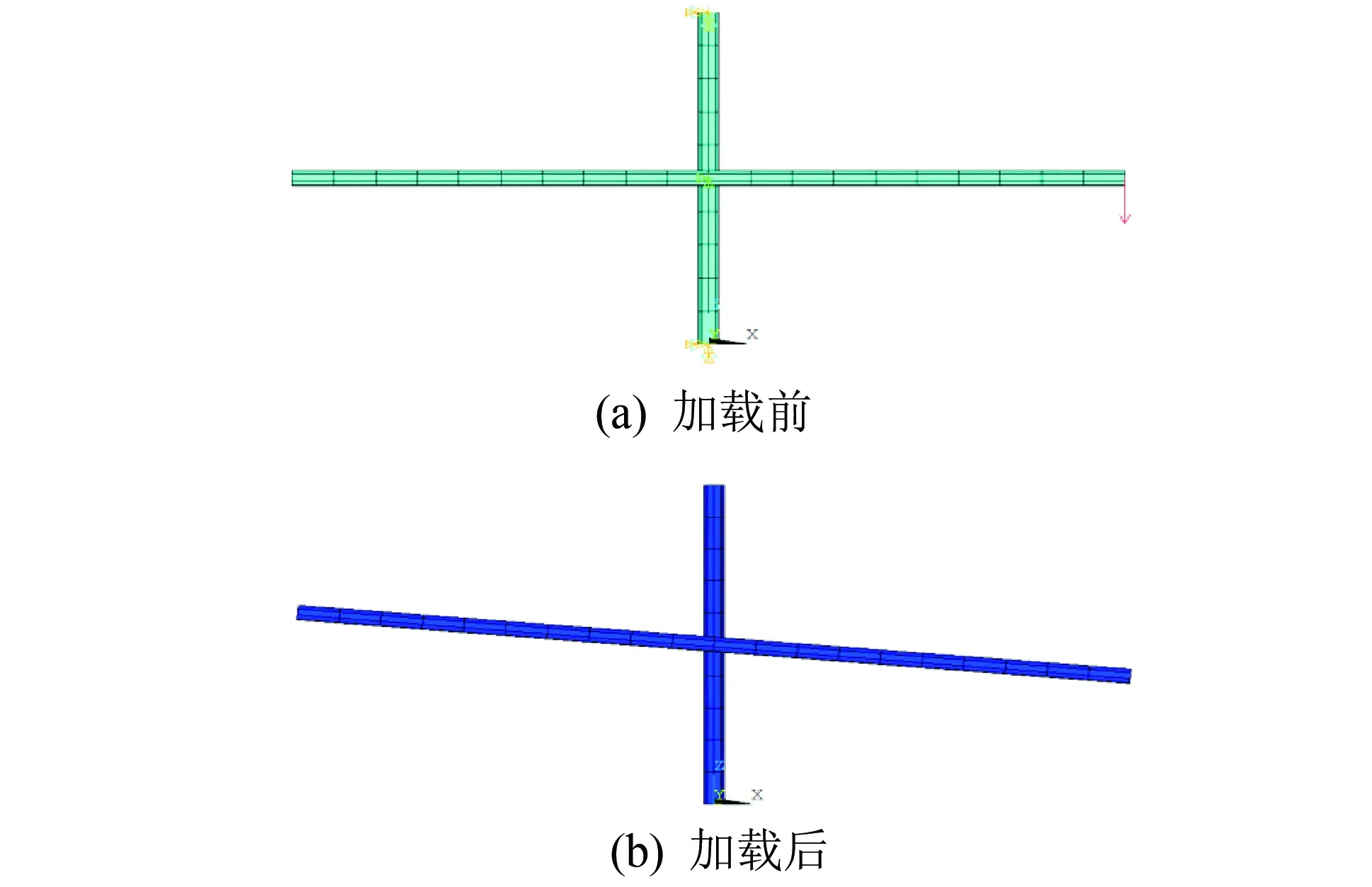
图6 扣件转动数值模拟Fig.6 Numerical simulation of coupler rotation

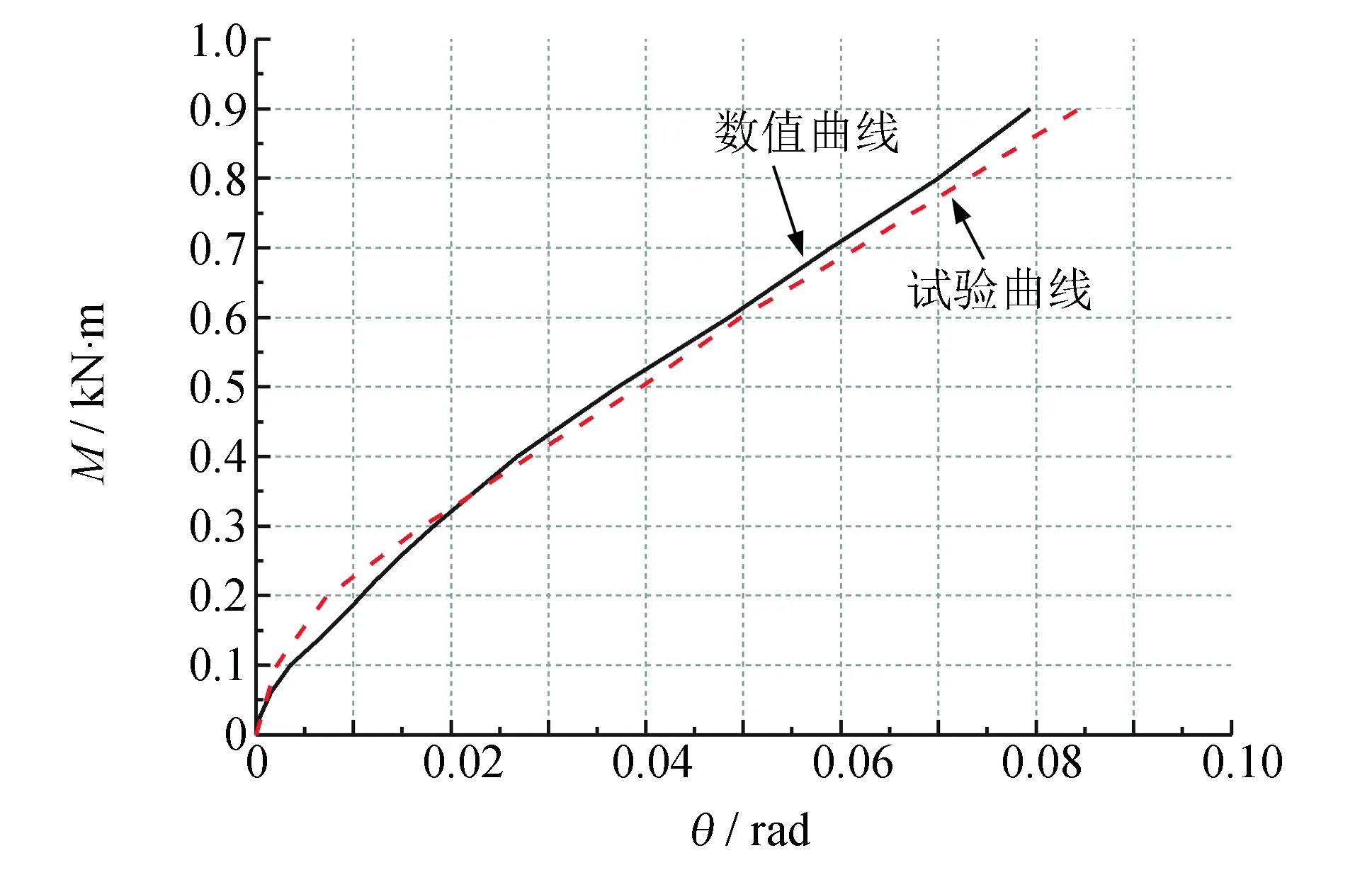
图7 扣件刚度弯矩-转角曲线Fig.7 Moment-rotation curve of coupler stiffness

4 结语

1) 通过对两个扣件式钢管满堂支撑体系的受力性能进行数值分析，结果表明，剪刀撑的设置对体系稳定承载力的影响显著，实际工程中必须设置剪刀撑.

2) 利用半刚性钢框架稳定理论对无剪刀撑的情况进行计算，结果与数值分析结果十分接近，说明半刚性钢框架理论适用于扣件式钢管满堂支持体系的计算.

3) 进行直角扣件转动试验，得到扣件转动刚度弯矩-转角曲线，并进行数值模拟.对于整体模型的承载力分析，还有待进一步改进.

[1] 袁雪霞，金伟良，鲁征，等． 扣件式钢管支模架稳定承载能力研究[J]． 土木工程学报，2006，39(5)：43-50．

[2] 谢楠，王勇． 超高模板支架的极限承载能力研究[J]． 工程力学，2008，25(增刊1)：148-153．

[3] BEALE R G.Scaffold research-A review[J].Journal of Constructional Steel Research, 2014, 98:188-200.

[4] ANDRE J, BEALE R G, BAPTISTA A M.A survey of failures of bridge falsework systems since 1970[J].Proceedings of ICE-Forensic Engineering, 2012, 165(4):161-72.

[5] 中华人民共和国建设部． 建筑施工扣件式钢管脚手架安全技术规范：JGJ 130-2011[S]． 北京:中国建筑工业出版社，2011．

[6] 陆征然． 扣件式钢管满堂支撑体系理论分析与试验研究[D]． 天津：天津大学，2010．

[7] 程华虎． 半刚性钢框架稳定分析及承载性能研究[D]． 南昌：南昌航空大学，2011．

[8] 屠凤莲，范顺成，罗文龙． 基于ANSYS的支撑架特征值屈曲分析[J]． 河北工业大学学报，2010，39(3)：6-10．

[9] PRABHAKARAN U.Nonlinear analysis of scaffolds with semirigid connections[D].Oxford:Oxford Brookes University, 2009.

[10] 朱启新，万雨辰，张其林． 钢管脚手架扣件节点的转动刚度试验和计算模型[J]． 山东建筑大学学报，2010，25(5)：499-518．

[11] 施炳华． 建筑施工现场模板支架与脚手架的设计计算[J]． 建筑科学，2007，23(7)：81-85．

(责任编辑：沈芸)

Ultimate load-carrying capacity analysis of Fastener steel tube full-hall formwork support systems on stability theory of semi-rigid steel frame

ZHUANG Mingzhi, FANG Sheng’en

(College of Civil Engineering，Fuzhou University，Fuzhou，Fujian 350116，China)

By considering semi-rigid properties of right angles couplers, material and geometry nonlinearity, the nonlinear buckling analysis were performed on two Fastener steel tube full-hall formwork support systems (no cross bracing model S1, cross bracing model S2), the vertical load-deflection curve of systems were obtained, and ultimate bearing capacity were determined.Stability theory of semi-rigid steel frame was used to calculate the bearing capacity of S1 model, the comparison of the result with the numerical result verified stability theory of semi-rigid steel frame is feasible in calculating bearing capacity of systems.Rotation performance of right angle couplers were tested, and moment-rotation curve of couplers were obtained.COMBIN39 spring element of ANSYS was used to simulate the rotation of right angle couplers.

fastener steel tube full-hall formwork support systems；nonlinear buckling analysis；semi-rigid steel frame stability theory；moment-rotation curve

2015-06-29

方圣恩 (1980-)，副教授，工学博士，主要从事结构健康监测与损伤识别，shengen.fang@fzu.edu.cn

福建省高校杰出青年科研人才培育计划资助项目(JA12020)；教育部留学回国人员科研启动基金资助项目(LXKQ201201)

10.7631/issn.1000-2243.2016.04.0557

1000-2243(2016)04-0557-06

U448.34

A