银行间网络模型与系统风险的分布式预警策略

王宗尧隋 聪

(1.东北财经大学萨里国际学院,辽宁大连116025; 2.东北财经大学金融学院,辽宁大连116025); 3.东北财经大学实验经济学实验室,辽宁大连116025)

银行间网络模型与系统风险的分布式预警策略

王宗尧1,隋 聪2,3

(1.东北财经大学萨里国际学院,辽宁大连116025; 2.东北财经大学金融学院,辽宁大连116025); 3.东北财经大学实验经济学实验室,辽宁大连116025)

通过对真实银行间借贷行为的数学抽象,建立了一个动态的银行间借贷网络模型.利用该模型,在计算机平台上,可以模拟仿真银行间市场.仿真的银行间市场能够展现出银行间资金流动等诸多规律,并能够用于研究银行间的流动性保护以及潜在的风险传染等规律性问题.同时,提出了分布式的银行间风险传染预警策略.利用分布式方法,将每家银行的风险特征映射成银行系统整体风险预警值,能够有效的解决中央预警方式的时滞性问题.仿真实验结果表明,银行的违约和风险传染并不是突发的,而是银行系统的风险累积的结果;分布式预警策略反映了银行系统内风险的累积过程,能够很好地预警银行系统性风险.

银行间市场;银行系统性风险;动态网络模型;风险传染

1 引 言

银行间市场为商业银行以及其他金融机构提供了一个管理流动性的手段.如果没有银行间市场存在,商业银行不得不持有大量超额准备金以应对无法预测的流动性需求.由于存在银行间市场,商业银行不需要持有大量的超额准备金.当超额准备金无法满足自身的流动性需求时,商业银行可以通过银行间市场借入资金,满足流动性;当超额准备金过剩时,商业银行可以通过银行间市场借出资金,获得收益.因此,银行间相互持有的债务形成了复杂的银行间网络.虽然,银行间市场为商业银行提供了彼此之间的相互保护.但是,银行间市场也为银行间的风险传染提供了渠道[1].银行间的风险传染是由银行间债务不能偿还所引起的.当一家银行没有办法偿还其银行间债务时,传染就产生了.给这家银行发放银行间贷款的银行,由于贷款无法收回可能导致其自身倒闭(被传染).同时,被传染的银行也无法偿还自身的银行间借款,从而产生多米诺连锁效应,引发系统性风险.2008年的美国次贷危机和2010年的欧债危机都已证明银行间网络的高度复杂性和不稳定性.这也引起了学者们对银行间网络的关注.

最早的银行间网络与风险传染的研究可以追溯到Allen等[2].他们研究认为银行间的风险传染力度和传染路径与银行间的拓扑结构有关.Freixas等[3]通过模拟对比了全连接的银行间网络和环形的银行间网络中风险传染.除了对规则网络进行研究,学者们还关注了随机网络中的风险传染.Nier等[4]将银行间网络模拟成随机网络,并分析了风险传染的影响要素以及传染进程.与此同时,学者们对真实银行间网络特征也进行了大量分析,并发现银行间网络都属于无标度网络(无标度网络的重要特征是节点度服从幂率分布).Boss等[5]分析了奥地利的银行间市场,研究发现该网络的度分布服从两阶段的幂律分布.Soramaki等[6]研究了美联储电子转移支付系统(Fedwire)中银行间网络,研究发现该网络节点入度和出度服从幂律分布.在对英国大额支付系统(CHAPS)的研究中,Becher等[7]发现虽然英国的银行数量远少于美国,但银行间网络节点度也有相似特征.同类研究还包括巴西的银行间市场[8],匈牙利的银行间市场[9],瑞士的银行间市场[10],荷兰的银行间市场[11],意大利的银行间市场[12].随后,学者们研究了无标度网络对银行间风险传染的影响[13,14].上述文献在银行间静态网络以及银行间风险传染等研究方面取得了许多进展,也为后续研究奠定了基础.

然而,银行间的债务具有高频性和动态性的特点.银行间的风险传染是一个积累、演化的过程.为了研究银行间风险的动态特征和传染特征,则需要从银行间债务的动态机制入手.为此,最近学者们在建立动态的银行间网络模型上进行了尝试.Iori等[15]认为银行的流动性冲击来自于客户存款与取款的随机行为,银行间借贷行为源自于银行的流动性需求并在此基础上,提出了动态银行间借贷的模拟规则.Afonso等[16]通过研究美联储电子转移支付系统,发现银行会根据自身备付金状况决定拆出资金并通过比例函数简化银行的决策,模拟了银行间的资金流动.Georg[17]的研究在区分主体异质性上做出了尝试.Georg[17]在Iori等[15]提出的动态规则的基础上,通过建立银行间决策的期望效用函数来区别不同银行的异质性问题.此外, Lenzua等[18]、陈冀等[19]对银行间网络结构的动态形成规律进行了研究,并在此基础上研究了银行间网络的风险传染问题.这些研究在探索银行间借贷的动态规则方面进行了有益尝试.

本文在文献[5,6,15,16]的基础上,建立一个银行间借贷的动态网络模型.该模型将真实的银行间借贷行为进行数学抽象,并以此建立一个仿真的银行间市场.这一动态网络模型通过对银行间市场的模拟,能够展现出银行间资金流动等诸多规律.并能够用于探索银行间的流动性保护以及潜在的风险传染等规律性问题.

此外，本文建立了一套即时、有效的银行间风险传染预警策略.传统的中央银行、银监会等监管机构收集信息并预测风险的中央式预警方法,存在明显的滞后性问题.银行间市场瞬息万变的特点导致了中央式预警方法作用十分有限.为此,本文采用分布式的方法建立预警策略.分布式方法在计算机领域有较为广泛的应用.所谓分布式就是在网络中没有中央系统进行管理,所有节点的运行都是通过彼此间的协调进行. Olfati-Saber[20]通过分布式的方式解决通讯网络中的信息流相互协调的问题.Wang等[21]利用分布式方法解决群体机器人之间的相互协调.Yang等[22]研究了通讯网络中的分布式控制方法.银行间网络中的资金协调与其他群体网络存在高度相似性.而且分布式方法的核心优势在于能够避免中央控制的滞后性问题.

2 银行间债务的动态网络模型

银行在经营管理过程中,期限错配是一个普遍现象.贷款的收回、客户的存款形成了银行的流动性供给.相反,客户的贷款需求、存款的提取构成了银行的流动性需求.通常情况,银行的流动性供给与流动性需求不会保持同步.这导致了商业银行超额准备金的波动[15].令ΔR表示商业银行的超额准备金变动.ΔR＞0表示流动性供给大于流动性需求,ΔR＜0表示流动性需求大于流动性供给.因此,银行i第t期的超额准备金表示为

研究银行间资金流动以及风险传染是本文的目的.为了简化而不失一般性,认为银行间的流动性供给和流动性需求是外生的并且是随机的.因此,假设超额准备金的波动是一个随机过程[17],令ΔRi=βi(ε-0.5),其中β表示银行系统外部的流动性冲击强度,i表示银行超额准备金的长期平均值,ε是一个随机变量,且ε∈[0,1].

在日常的流动性管理中,银行首先要考虑偿还上一期的银行间借款.如果所有银行都偿还上一期的银行间借款,那么银行就可以同时完成上一期银行间借款的偿还和银行间贷款的回收.所以,银行的超额准备金变为

假设银行系统内有M家银行.令表示第t-1期银行i贷给银行j的资金,那么银行间债务关系可以用债务矩阵Lt-1来表示,即

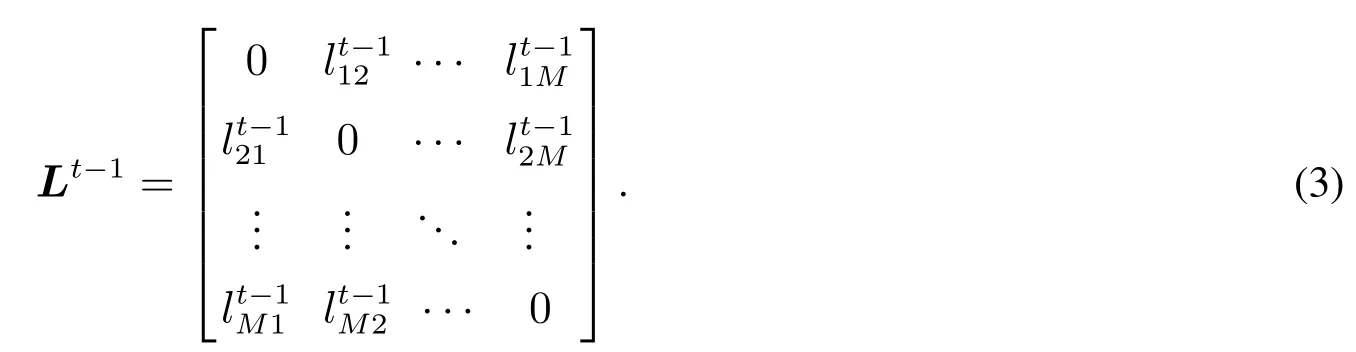
对于银行i而言,第t-1期银行间贷款总量可以表示为第t-1期银行间借款总量可以表示为

在清算完上一期银行间债务后,如果银行有多余的超额准备金,则会通过银行间市场贷给其他银行;如果银行缺少超额准备金,则会通过银行间市场借入资金.就银行间网络整体而言,银行间资金的贷出和借入是同时发生的.因此,只需考虑银行间资金的贷出.

其中i=1,2,...,M.

式(4)表示银行超额准备金为正时,它可以为其他银行提供流动性资金.并且银行会将超额准备金的θ倍贷出,0＜θ＜1.令表示银行i给银行j的贷款比例,.银行i给银行j的贷款可以表示为

McAndrews等[23]、Afonso等[16]的研究表明,银行间市场一天的交易是从银行获得资金到贷出资金的不断循环.也就是说,银行间的借贷是从式(4)到式(6)的不断循环和更新,直到当天的银行间市场关闭.在一天的交易结束后,银行必须保证超额准备金表明银行出现流动性赤字.这将导致银行的法定准备金不足.为此银行会受到中央银行严厉的惩罚.同时,流动性赤字还会导致银行间债务的违约.债权银行无法及时收回银行间贷款也将出现流动性问题,从而形成流动性风险在银行间的传染.下文将在计算机平台上,建立仿真银行间市场,模拟银行间资金流动的动态过程.

3 银行间风险传染预警策略

3.1 银行的流动性风险

银行日常流动性管理的关键是保持合适的流动性储备,也就是将超额准备金Rti控制在合理的范围内.在正常运营的情况下,银行的超额准备金的变化是相对稳定的.如果银行间由于自身的管理问题导致流动性需求大于流动性供给,将会导致银行超额准备金减少.与此同时,如果银行不能在银行间市场获得足够的流动性支持,将会造成银行超额准备金的持续减少.最终将导致银行出现流动性赤字.可见,银行出现流动性问题是一个累积的过程.令表示银行i在t时期的超额准备金的变动率,即

显然,一个流动性管理很好的银行,累积超额准备金的变动率应该保持在0附近.如果银行超额准备金持续减少,累积超额准备金的变动率会越来越小.该指标能够反映银行流动性风险的积累过程.

式(8)累积超额准备金变动率可以对单个银行的潜在流动性风险做出一定的预测,但是仍无法预测整个银行系统的风险水平.为了阻止风险传染扩散,防止爆发系统性风险和稳定金融网络,必须对整个银行系统的风险水平进行预测.第一,从宏观角度,只有金融监管部门及时、准确地得到了整体风险的预测信息,才能有效地进行市场干预,防止危机爆发.第二,从微观角度,银行仅掌握自身的风险状况是不够的.银行还需要了解金融网络的整体风险,以及时调整自身策略防止被传染.

3.2 分布式预警策略

银行系统是一个典型的分布式系统.银行每天都会处理大量的信息并进行经营决策.由于在银行间市场上资金的转移和信息的传播具有快速性和大量性的特点,导致中央机构很难及时的收集到足够的信息进行整体风险预测.而且滞后的信息对预测是没有任何意义的.

压缩压力、圧缩温度和燃油喷射系统(喷油时刻、喷射压力、燃油品质等)等影响喷入缸内燃油的雾化及油气混合的形成，从而导致燃烧时刻变化,尤其是喷油时刻对燃烧时刻起着决定性的作用，燃烧时刻的异常也直接关系到燃烧爆压和后期燃烧性能。

分布式方法则是将每个节点自身的某种属性,结合网络的拓扑,映射成网络的整体属性.这一映射过程是通过节点间的联系实时完成的.银行间网络中分布式预警策略就是将每个银行的流动性风险信息,映射成银行间网络的整体风险特征.同时,这个过程并不需要中央机构收集信息,而是在银行间的资金转移的过程中同步完成.因此可以有效的避免时滞性问题.

假设银行i和银行j之间有资金往来.pi和pj分别表示两家银行累积超额准备金的变动率,它们分别代表了两家银行的流动性风险信息.这两家银行分布式预警的映射过程也可以理解为两家银行的风险信息交换过程,表示为

其中k为迭代次数,Δk=1,κ∈(0,1)是系统参数.

式(9)是对两家银行各自风险信息不断迭代的过程.经过k次迭代以后,银行i可以获得新的风险信息而新的风险信息则代表了两家银行总体风险特征.如果银行i与Ni家银行有资金往来,则分布式预警映射过程可以表示为

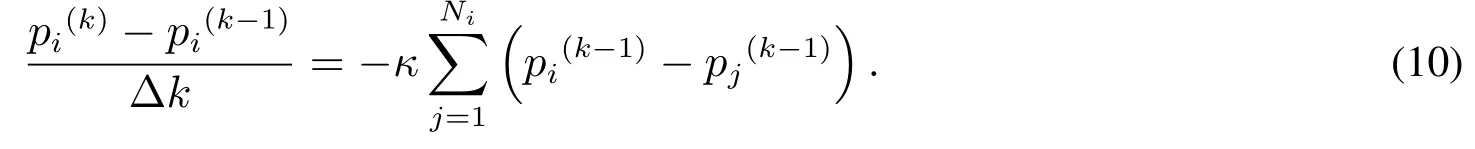
通过式(10)的迭代过程,银行i获得的新的风险信息则代表了银行i与所有邻居银行的整体风险特征.根据文献[21],考虑网络中所有银行,则分布式风险预警映射过程可以表示为

其中P=[p1,p2,...,pM]T表示银行累积超额准备金的变动率向量.Λ表示网络拓扑结构的拉普拉斯矩阵,Λ=Δ-A.A是银行间网络的邻接矩阵,Δ是邻接矩阵的度矩阵,其对角线元素是节点的度,其余元素为0.式(11)就是银行间风险传染的预警策略.通过式(11)的迭代过程,每家银行都可以获得新的风险信息p*.p*作为银行系统整体风险的预警指标,反映了银行间网络的整体风险特征.p*＜0表明银行间存在风险传染的可能性,而且p*越小风险传染可能性越大.通过拉塞尔稳定性原理可以证明式(11)的迭代过程是可以稳定收敛的[21].也就是说,所有银行将获得同样的银行间网络整体风险特征.因此,通过该策略银行可以根据自身的风险信息pi以及网络整体风险特征p*进行自身的流动性管理.

4 仿真模拟实验

4.1 参数设定

银行持有超额准备金数量体现了银行的规模.并且银行超额准备金数量与债务连线数量成指数函数关系[6].本文根据BvD Bankscope数据库的中国银行业数据,利用指数函数初始化银行超额准备金数量[14].超额准备金最大值25 298亿元、最小值800亿元,分别对应最大债务连线银行和最小债务连线银行.银行超额准备金的长期平均值与初始化的银行超额准备金相同.初始期所有银行都没有银行间债务,即IL=0,IB=0.银行在每期中贷款支付比例采用文献[16]的基础设置,θ=0.8.在每期中,银行间贷款支付循环次数设定为20次.

在本文的模拟中,银行间网络运行的期数设定为500期.从模拟结果来看,流动性冲击强度β＜0.5时,不会出现银行违约以及传染.为了检验预警策略的效果,本文模拟了银行间网络的两类情况:平稳期,β∈[0.1,0.4];危机期,β∈[1.4,1.7].预警指标累积超额准备金的变动率的累积期数选为10期.

4.2 平稳期的模拟结果

在平稳期的实验中,选择了四种流动性冲击强度,分别为0.1,0.2,0.3和0.4.在这四种流动性冲击强度下,整个银行间网络都是相对平稳的,没有出现银行违约.当银行系统的流动性冲击强度较小时(β＜0.5),

银行间市场为商业银行提供的彼此之间的相互保护能够吸收掉系统外部的冲击影响.从而保证整个银行系统的正常运行.

在这组实验中,当银行有多余的超额准备金时,银行能够将超额准备金贷给系统内其他银行.当银行超额准备金不足时,银行可以通过银行间市场获得必要的流动性.这一过程保证了银行系统内的整体超额准备金水平能够相对保持稳定.银行系统内超额准备金变动表示为

图1展示了四种流动性冲击强度下,银行系统内整体超额准备金变动情况.

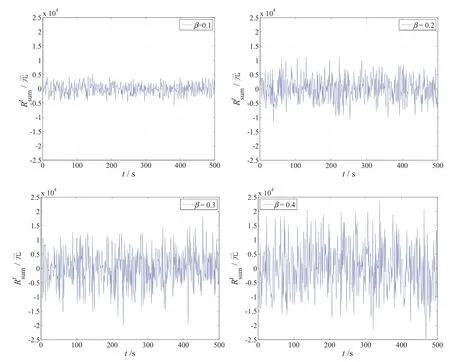
图1 银行系统内超额准备金变动情况Fig.1 Interbank systemic excess reserve changing

尽管在这四种冲击下都没有出现银行违约,但是冲击的差异也导致了银行系统内部出现一些变化.随着银行系统外部的冲击的加强(流动性冲击强度从0.1到0.4),银行系统内整体超额准备金波动明显增强.当流动性冲击强度为0.1时,银行系统内整体超额准备金在(-5 000,+5 000)内波动.当流动性冲击强度为0.4时,银行银行系统内整体超额准备金波动超过了(-20 000,+20 000).

在不同冲击强度下,银行系统内变化还体现在银行间网络的整体风险p*上.如前所述,通过分布式预警策略,对每家银行的累积超额准备金的变动率进行映射,可以获得银行间网络的整体风险p*.p*反映了银行系统的整体风险水平.图2展示了四种流动性冲击强度下,银行系统的整体风险水平的变化情况.

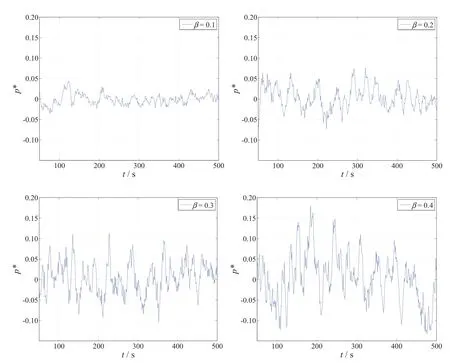
图2 银行系统性风险预警指标(p*)的变化情况Fig.2 Interbank systemic risk index(p*)changing

从图2可以看出,随着银行系统外部冲击的加强(流动性冲击强度从0.1～0.4),银行系统的整体风险的波动也明显增强.当流动性冲击强度为0.1时,银行系统的整体风险最小值大于-0.05.当流动性冲击强度为0.4时,银行系统的整体风险最小值大于-0.15.一旦银行系统的整体风险最小值突破某一阈值,银行系统将出现违约及传染.

4.3 危机期的模拟结果

为了模拟危机时期的银行系统,重新选择了四种流动性冲击强度,分别为1.4,1.5,1.6和1.7.在这四种流动性冲击强度下,整个银行体系出现了不同程度的损失.此时,银行间市场不再为商业银行提供的彼此之间的相互保护,而是成为了银行间风险传染的渠道.为了显示银行体系的损失程度,分别记录了四种冲击下累积违约银行的数量,见图3.从图3可以看出,当银行系统受到强烈冲击(β≥1.4)时,随着时间的推移银行系统内累积违约银行数量不断的增加.总体来看,冲击越大,违约银行的数量越大,违约传染的速度越快.

接下来,检验分布式预警策略的效果.首先,通过分布式预警策略计算银行间网络的整体风险p*,将其作为银行系统整体风险的预警指标.其次,记录银行系统中银行的违约比率.

图4展示了银行系统整体风险的预警指标p*和银行的违约比率.为了达到更好的展示效果,将违约率进行了数量级的调整.图4中虚线代表银行的违约比率,实线代表预警指标p*,阴影表示预警指标p*小于0的部分.

图3 银行系统的累积违约银行数量(Nb)Fig.3 Interbank systemic cumulative default institutes number(Nb)

从图4中可以得出两个结论.第一,阴影越大银行违约比率约大.阴影代表了预警指标p*小于0的部分.也就是说,银行间网络的整体风险p*越小,银行违约的风险越大.第二,在银行系统内出现违约之前,银行间网络的整体风险p*普遍存在下降的过程.银行间网络的整体风险p*是由每家银行的累积超额准备金变动率映射而来.累积超额准备金变动率反映了单个银行的风险累积过程.从而,整体风险p*揭示了银行系统的风险累积过程.从实验结果来看,银行系统内的违约风险并不是突然产生的,而是风险累积的结果.本文提出的分布式预警策略能够很好地反映出银行系统内风险累积过程,能够起到对银行系统性风险预警的作用.

5 结束语

银行间债务违约引发风险传染最终导致系统性风险的问题越来越受到关注.许多文献开始利用网络理论研究银行间的风险传染和系统性风险问题.本文建立了银行间借贷的动态网络模型以及仿真的银行间市场.利用银行间借贷的动态网络模型对银行间市场进行仿真模拟,能够展现出银行间资金流动等诸多规律.这也为探索银行间的流动性保护以及潜在的风险传染等规律性问题提供了可能.此外,本文提出了银行间风险传染的预警策略.该预警策略利用分布式方法,将每家银行的累积超额准备金变动率映射成反映银行系统整体风险特征的预警指标.分布式预警策略的最大优势在于,能够有效的解决中央预警方式的时滞性问题.仿真实验结果表明,外部冲击加强会导致银行系统内整体超额准备金波动加剧.整体超额准备金波动加剧会导致系统内银行的违约以及风险传染.银行的违约和风险传染并不是突发的,而是银行系统的风险累积的结果.本文提出的分布式预警策略能够很好地反映出银行系统内风险的累积过程,并能够起到银行系统性风险预警的作用.

[1]Upper C.Simulation methods to assess the danger of contagion in interbank markets.Journal of Financial Stability,2011,7(3): 111–125.

[2]Allen F,Gale D.Financial contagion.Journal of Political Economy,2000,108(1):1–33.

[3]Freixas X,Parigi B,Rochet J C.Systemic risk,interbank relations and liquidity provision by the central bank.Journal of Money, Credit and Banking,2000,32(3):611–638.

[4]Nier E,Yang J,Yorulmazer T,et al.Network models and fnancial stability.Journal of Economic Dynamics and Control,2007,31(6): 2033–2060.

[5]Boss M,Elsinger H,Summer M,et al.Network topology of the interbank market.Quantitative Finance,2004,4(6):677–684.

[6]Soramaki K,Bech M,Arnold J,et al.The topology of interbank payment fows.Physica A,2007,379(1):317–333.

[7]Becher C,Millard S,Soramaki K.The Network Topology of CHAPS Sterling.London,UK:Bank of England,No.355,2008.

[8]Edson B,Cont R.The Brazilian Interbank Network Structure and Systemic Risk.Brazilia:Central Bank of Brazil,No.219,2010.

[9]Lublóy A.Domino effect in the Hungarian interbank market.Hungarian Economic Review,2005,52(4):377–401.

[10]Müller J.Interbank credit lines as a channel of contagion.Journal of Financial Services Research,2006,29(1):37–60.

[11]Van Lelyveld I,Liedorp F.Interbank contagion in the Dutch banking sector:A sensitivity analysis.International Journal of Central Banking,2006,2(2):99–133.

[12]Mistrulli P E.Assessing fnancial contagion in the interbank market:Maximum entropy versus observed interbank lending patterns. Journal of Banking and Finance,2011,35(5):1114–1127.

[13]Krause A,Giansante S.Interbank lending and the spread of bank failures:A network model of systemic risk.Journal of Economic Behavior and Organization,2012,83(3):583–608.

[14]隋 聪,迟国泰,王宗尧.网络结构与银行系统性风险.管理科学学报,2014,17(4):57–70. Sui C,Chi G T,Wang Z Y.Network structure and banks systemic risk.Journal of Management Sciences in China,2014,17(4): 57–70.(in Chinese)

[15]Iori G,Jafarey S,Padilla F.Systemic risk on the interbank market.Journal of Economic Behavior&Organization,2006,61(4): 525–542.

[16]Afonso G M,Shin H S.Systemic risk and liquidity in payment systems.Federal Reserve Bank of New York,2008,No.352.

[17]Georg C.The effect of the interbank network structure on contagion and common shocks.Journal of Banking and Finance,2013, 37(7):2216–2228.

[18]Lenzua S,Tedeschib G.Systemic risk on different interbank network topologies.Physica A,2012,391(18):4331–4341.

[19]陈 冀,陈典发,宋 敏.复杂网络结构下异质性银行系统稳定性研究.系统工程学报,2014,29(2):171–181. Chen J,Chen D F,Song M.Heterogeneous bank system stability research under complex networks structure.Journal of Systems Engineering,2014,19(2):171–181.(in Chinese)

[20]Olfati-Saber R.Flocking for multi-agent dynamic systems:Algorithms and theory.IEEE Transacation on Automatic Control,2006, 51(3):401–420.

[21]Wang Z,Gu D.Cooperative target tracking control of multiple robots.IEEE Transacation on Industrial Electronics,2012,59(8): 3232–3240.

[22]Yang Q,Barria J,Green T.Communication infrastructures for distributed control of power distribution networks.IEEE Trans.on Industrial Informatics,2011,7(2):316–327.

[23]McAndrews J,Potter S M.Liquidity Effects of the Events of September 11,2001.FRBNY Economic Policy Review,2002,8(2): 59–79.

Interbank network model and distributed prediction strategy of systemic risk

Wang Zongyao1,Sui Cong2,3
(1.Surry International Institute,Dongbei University of Finance and Economics,Dalian 116025,China; 2.School of Finance,Dongbei University of Finance and Economics,Dalian 116025,China; 3.Laboratory of Experimental Economics,Dongbei University of Finance and Economics,Dalian 116025,China)

A dynamic interbank loan model is established by mathematical abstraction for real bank lending behavior.By using this model,the behavior of interbank can be realistically simulated via computer platform.Through the simulation,it is found that a lot valuable regulation of interbank which can be used to study liquidity protection and potential risk.Meanwhile,this paper also presents a distributed banking systemic risk prediction strategy.Using the distributed method this strategy maps the risk character of banks to banking system risk index.This method can effectively solve time-delay of centralized prediction strategy.The simulation results show that the bank default and risk contagion is not an emergency even,but an accumulated result.The presented strategy can also refect the accumulated process and precisely predict the banking system risk.

interbank market;banking systemic risk;dynamic network model;risk contagion

F830

A

1000-5781(2016)06-0840-10

10.13383/j.cnki.jse.2016.06.012

王宗尧(1980—),男,黑龙江哈尔滨人,博士,副教授,研究方向:分布式系统控制,Email:zongyaowang@dufe.edu.cn;

2016-01-25;

2016-04-18.

国家自然科学基金资助项目(71571034;61304180);教育部人文社会科学研究青年基金资助项目(12YJCZH211);辽宁省高等学校优秀人才支持计划资助项目(WJQ2015012).

隋 聪(1978—),男,辽宁沈阳人,博士,副教授,研究方向:金融风险管理,Email:suicong2004@163.com.