“情境—变式”教学对学生思维能力影响之研究

陈德煜

摘 要： 在数学教学中，问题设置要注重学生提出问题能力培养，本文提出“情境-变式”教学模式，从问题数量、问题种类、问题新颖性及问题变式角度阐述对学生思维能力的影响。

关键词： 情境 变式 思维能力

一、引言

在数学教学中，问题设置要注重学生提出问题能力培养，提出问题指：“通过对情境的探索产生新问题，或在解决问题过程中对问题的再阐述。”其实质就是一种以问题生成为基本形式的数学探究活动。问题解决是数学教学重点，尤其是解题教学。解题教学需要学生具备较高问题意识，问题意识会影响数学问题解决，随着“问题解决”研究的深入开展，局限性日益表现出来，而作为“问题解决”前提的“提出问题”日益受到广泛重视。因此，如何培养学生提出问题的能力，笔者在课堂教学中尝试“情境-变式”教学，对它能否提高学生思维能力，进行了一番研究。

二、“情境-变式”教学模式

“情境-变式”教学模式如图1所示：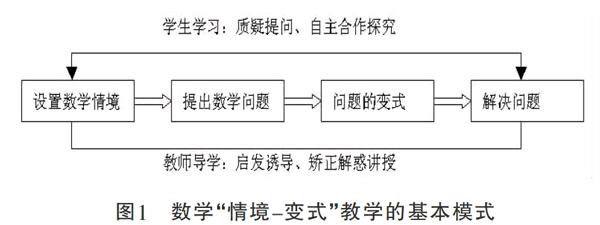

1.创设数学情境：问题提出（Problem-posing）是人们基于一定情境，通过对情境中已有数学信息的观察、分析，产生质问、困惑，进而发现和产生新的数学任务或数学问题的过程。国内贵州师范大学吕传汉教授在问题情境创设方面做了大量研究，情境是问题的根，问题是情境的心。学生探究学习中的情境与问题是相辅相成的，是一个因果联系的有机体。

2.提出数学问题：事实上，研究者已从托伦斯创造性思维测验（Torrance test of creative thinking ）中得到启发，对提出问题能力有了新的认识，即用以表征提出问题能力的三要素：问题的数量、问题的种类、问题的新颖性。一个学生提出的问题数量较多，表明他在收集和处理问题信息时能产生大量有价值和意义的联想。当然，关注学生能否从不同角度提出不同问题，对提高学生思维的灵活性是十分必要的。对问题新颖性的判断，要注重问题原创性和合理性，检测学生思维的创造性。

3.问题的变式：变式教学是我国数学教育的一个特色。“变式”是在保持一事物本质属性不变的前提下，通过变换它的非本质属性，突出它的本质属性的一种思维方式。问题变式教学特征是：通过问题各种变式之间或改条件，或改结论等方式，掌握问题之间的差异与联系，认识问题的内涵与外延，实现对问题多角度的理解。在数学活动过程中，通过多层次推进，使学生渐进形成解决问题，从而形成多层次活动经验系统[3]。

4.解决问题：有两个方面事实：一是学生收集和处理问题信息条件；二是学生提出问题的动机。基于以上两个事实，学生提出问题的能力必需有较强思维能力。

三、教学案例分析

以数学研究性学习课题为载体，进行情境学习在数学课堂中的案例分析。

创设问题情境：一根长5米的竹竿斜靠在墙面，上端下滑1米，下端滑行多少米？

先让学生猜测，然后实际验证。发现不同结论后，同学们专心致志地用数学知识进行探究、讨论，提出了一系列问题（有的是数学问题，有的是非数学性问题）：

（1）问题1：一根长5米的竹竿，斜靠在墙面上（与地面夹角α°>45），上端下滑1米，下端也滑行1米，这根竹竿是如何斜靠的？

变式1：一根长5米的竹竿，斜靠在墙面上（与地面夹角α°<45），上端下滑1米，下端也滑行1米，这根竹竿是如何斜靠的？

（2）问题2：一根长5米的竹竿，斜靠在墙面上（与地面夹角α°>45），有没有可能上端下滑1米，下端滑行大于或小于1米？

变式2：一根长a米的竹竿，斜靠在墙面上（与地面夹角α°>45），有没有可能上端下滑1米，下端滑行大于或小于1米？

（3）问题3：一根长为a米的竹竿，以和地面夹角α°>45斜靠在墙面上，有没有可能上端下滑距离与下端滑行距离一样？

学生在这一系列问题提出和解决中获得从不同角度提出问题的学习体验.

四、“情境-变式”教学对学生思维能力影响研究

研究对象为我校高一年级两个班的学生，这两个班学生各条件平均，属于平行班。实验前，对实验班与对比班进行数学试题测试，并对数据进行分析（表1）。

从表1可以看出，实验班与对比班平均分相差1.2分，计算t值为-1.48<1.96，说明实验班与对比班在测试平均成绩上无显著差异，标准差接近相等，实验班与对比班学生分布均匀。

（1）实验自变量：“情境-变式”教学。

（2）实验因变量：学生思维能力的变化。

（3）实验材料：搜集有用的题项，最后修订成为简式思维能力测试量表（SAIS），以此编制学习思维能力特征调查问卷，在此基础上，征求心理专家意见进行题项修订，形成预试问卷，对预试问卷进行探索性因素分析并进行因素命名，得到正式问卷。对正式问卷进行信度、效度检验，编制28道题目，从影响“思维能力”问题的数量（1-7）、问题的种类（8-17）、问题的新颖性（18-28）3个维度对学生进行测试，每维度采用李克特记分法，分5级记分法，从“非常符合”到“非常不符合。

（4）实验结果分析：

五、结语

表2为独立样本t检验的结果，平均数差异检验的基本假设之一就是方差同质性，因而在进行t检查之前，会先进行两组离散状况是否相似的检验，当两个群体方差相同时，则称两个群体间具有方差同质性。在前测中，三个维度的T值分别为：8.852（S1）、6.425（S2）、7.254（S3）、3.145（总分），三者的T值为0.05，不显著。在后测中，三个维度的T值分别为：5.89（S1）、9.34（S2）、2.34（S3）、4.36（总分），问题的数量、问题的种类、问题的新颖性显著性水平在0.05上显著。通过“情境-变式”教学，确实能提高学生的思维能力。

“情境-变式”教学1、2环节中，学生首先通过观摩问题的情境，教师提出任务要求，组织学生互相讨论，激发学生的思想碰撞，最终提出一系列问题，有些问题可能是数学性的，也有可能是非数学性的，这些都应该肯定学生的学习热情，问题的数量可体现学生思维的流畅性，让学生的思维得到充分发散，提高学生的思维品质。在“情境-变式”教学3环节中，通过对问题的变式，变换非本质属性，种类繁多，培养学生思维灵活性和创造性。

总而言之，情境创设要隐藏学生能发现的一些数学问题，并联系“生活现实”。创设日常生活情境进行教学，对提高学生学习数学的兴趣，掌握数学的来源，理解数学抽象模型，很有好处。同时，利用反例、辨析题和变式题进行教学属于变式教学范畴，反例的特点是改变对象的本质属性而保持非本质属性不变，辨析题的特点是改变对象的非本质属性而保持本质属性不变。

参考文献：

[1]波利亚，阎育苏译.怎样解题[M].北京：北京科学出版社，1982.

[2]朱仁江.初中数学问题结构式变式教学的实践研究[J].中学数学杂志初中版，2007（3）.

[3]吕传汉，汪秉彝.中小学数学情境与提出问题教学探究[M].贵阳：贵州人民出版社，2002.

[4]吴华，马东艳.多媒体技术与数学“情境—问题”教学[J].数学教育学报，2008，17.