基于Kriging与GA的双层变模温注射成型收缩控制策略

王梦寒，刘晓，危康，李雁召

（重庆大学材料科学与工程学院，重庆 400030）

基于Kriging与GA的双层变模温注射成型收缩控制策略

王梦寒，刘晓，危康，李雁召

（重庆大学材料科学与工程学院，重庆 400030）

高温、高压的成型条件，使双层变模温制品的成型收缩对工艺参数的变化极为敏感，双层变模温制品的成型收缩控制策略成为提高制品质量的关键。以某空调遥控器前盖双层变模温成型工艺开发为例，探讨并制定了其成型收缩的控制策略。确定了考量成型收缩的多目标评价体系及参数变量，以拉丁超立方取样设计试验，并利用数值模拟软件进行充模、保压及冷却等过程模拟获取试验数据，建立了基于 Kriging代理模型的变量与评价指标间的数学关系；利用遗传算法对数学关系进行迭代，寻找最优成型收缩的评价指标及变量组合；最后，将模拟及生产试验对研究策略的科学有效性进行验证。

双层变模温成型；收缩控制；Kriging模型；遗传算法；数值模拟

引 言

成型收缩作为影响注塑制品的几何与尺寸精度的关键因素，将导致翘曲变形、表面沉降等问题。双层变模温注射成型是指将双色叠层注射[1-2]与快速变模温技术[3-4]相结合的成型方法，双层制品的材料间结合强度和表面光亮度有较高要求，高温、高压的成型条件，使其制品的成型收缩对工艺参数的变化极为敏感，双层变模温制品的成型收缩控制策略成为提高制品质量的关键。

为探究双层变模温注射成型中成型收缩的控制方法，国内外学者进行了相应的研究。在双层成型方面，Arzondo等[2]对PP、EOC、LDPED塑料在不同温度和压力条件下进行双层注射成型，通过对成型试样进行标准剥离试验，分析工艺参数对结合强度的影响，并对工艺参数进行寻优处理。Jiang等[5]、Nguyen等[6]、Yan等[7]均对不同材料的双色双层成型进行研究，从材料间表面结合强度出发，分析成型温度、压力等工艺参数对结合强度的影响规律。可见，双层成型的结合强度至关重要。陈茂顺[8]对时序控制浇口的双层高光成型进行研究，以体积收缩率和缩痕指数为评价指标，对成型过程工艺参数进行了分析。变模温成型方面，Wang等[3,9-10]、Nian等[4]均对模具的温控系统进行了研究，以获取均匀的模具温度和较高的加热效率。Xiao等[11]通过结合粒子群和有限单元相结合的方法，对加热系统进行优化设计，提升了加热效率和型腔表面温度分布的均匀性，最终提升了制件的表面质量。刘冬雷等[12-13]以车载高光蓝牙外壳为例，研究了模具温度及相同/不同模具温度下其他成型参数对变模温制品表面沉降的影响规律。Lucchetta等[14]研究发现变模温技术下，塑料熔体可以精确地复制模具表面形貌，并能控制熔接痕和应力松弛等表面缺陷的发展。

双层变模温成型作为注射成型的新工艺，成型过程工艺参数控制困难、成型收缩对工艺参数非常敏感，关于双层变模温成型参数控制研究的文献较少，对其成型收缩的控制也鲜见报道。因此，本文针对双层变模温的成型收缩问题，从成型工艺参数条件入手，制定将Kriging建模和遗传算法相结合的成型收缩控制策略，并将优化控制结果应用于模拟试验和实际生产，为双层变模温注射成型工艺参数制定及成型收缩控制提供参考。

1 双层变模温成型收缩的问题描述及研究策略

1.1 产品模型及问题的描述

为探讨双层变模温注射成型收缩控制策略，论文以某空调用遥控器前盖双层变模温成型工艺收缩控制进行研究。空调遥控器前盖产品模型如图1所示，该产品内外两层通过双层注射工艺直接成型，外层为透明的PC塑料、内层为白色的ABS塑料。因该产品是两种材质的包覆结构，注射成型时，确定外层为先行变模温注射的成型层、内层为二次重叠注射的双层注射成型充填顺序。

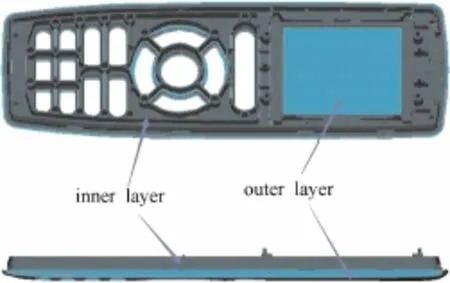
图1 遥控器前盖产品模型Fig.1 Product model of remote control's front cover

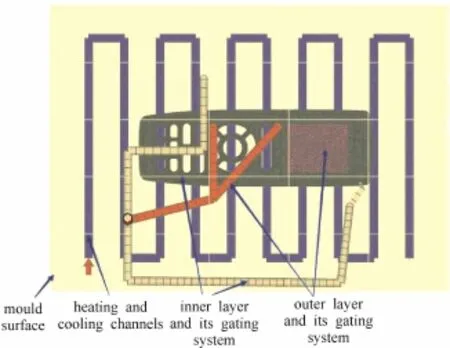
图2 遥控器前盖双层变模温成型模拟模型Fig.2 Bi-layer RHCM simulation model of remote control's front cover of air conditioner

顶出时体积收缩率是零件从冷却阶段结束到冷却至环境参考温度时局部体积的减小量，以原始建模体积的百分比形式来表达各区域的体积收缩率，它能较好地反映制件的成型收缩，本文将以顶出时体积收缩率为产品收缩的衡量指标开展研究。为明确空调遥控器前盖双层变模温注射成型过程中收缩变化，论文选用Moldflow模拟分析软件，建立了如图2所示的模拟分析模型，利用系统推荐的参数组合对其充填、保压及冷却等过程进行了模拟，获得了如图3所示的顶出时体积收缩率。由图3可知，PC材料收缩最大值为10.97%，ABS材料收缩最大值为6.72%，两者的收缩都偏大，其差值高达4.25%。这将对两种材料的结合性及外观造成很大的影响，由于两者的体积收缩率相差太大，最终的双层产品也很容易发生翘曲变形。

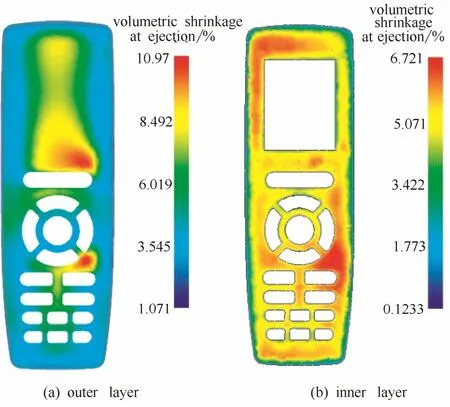
图3 初始成型的顶出时体积收缩率Fig.3 Volumetric shrinkage at ejection of initial simulation

1.2 控制策略的制定

为对双层变模温的成型收缩进行控制，本文拟分析成型工艺条件的影响，并通过寻找成型过程的最优变量组合，来达到成型收缩控制的目的。由于双层变模温成型过程中成型收缩的复杂性，为此需要对评价收缩的多目标体系进行分析，确定适当的收缩评价指标及控制变量。为了对问题进行定量分析，本文拟建立控制变量与目标间的数学模型。但多变量对目标的影响是典型的复杂问题，难以找到其显函数形式。因此，引入预测模型来建立变量与目标之间的数学关系。由于Kriging 模型可以在小样本情况下保证拟合精度，对于非线性问题预测有较高的精度，在核函数的作用下，具有局部估计的特点；考虑本文的收缩控制问题具有非线性和小样本建模等特点，选用Kriging代理模型[15-16]进行数学关系的建立。但数学关系并不能直接给出收缩控制的最终优化结果。因此，引入遗传算法（genetic algorithm，GA）[17-18]对Kriging模型进行迭代寻优，得出优化后评价指标及对应变量，从而实现双层变模温成型的收缩控制。为此，制定了如图4所示双层变模温成型收缩控制的研究策略。

该优化策略的主要步骤如下。

（1）确定评价体系及变量。建立有限元模拟模型，进行初始模拟试验，确定控制目标，建立策略的多目标评价体系，并确定控制变量。

（2）建立并检验Kriging近似模型。利用拉丁超立方抽样试验进行 Kriging模型的建立，并对模型进行可靠性检验。

（3）遗传算法寻优。利用遗传算法，对Kriging模型进行迭代寻优，寻找最优成型收缩评价指标及对应控制变量组合。

（4）策略可行性验证。对寻优结果进行模拟及生产试验，以验证控制策略的科学有效性。

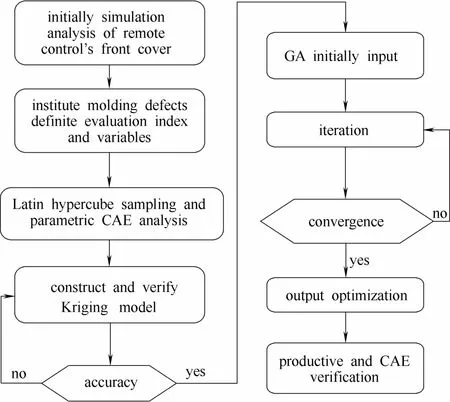
图4 双层变模温成型收缩控制策略的技术路线Fig.4 Approach of molding shrinkage control strategy

2 实验结果与讨论

2.1 制定评价体系及变量

如前所述，确定评价指标是收缩控制策略的首要任务。考虑双层注射成型过程中，两种物料均会发生收缩且相互作用和影响，其控制则包括降低物料的收缩值和让两种物料的收缩值趋近两个方面，确定以PC的顶出时体积收缩率Y1(%)，ABS的顶出时体积收缩率 Y2(%)来衡量两种物料各自的收缩值，并以Y1与Y2的差的绝对值Y3来衡量两种物料收缩值的趋近程度。由此，采用加权法得出收缩控制的综合评价指标Y，如式(1)所示。

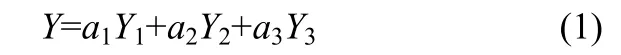
其中，a1、a2、a3分别表示Y1、Y2、Y33个评价分量的权重，a1Y1和a2Y2用来保证两种材料的收缩率低，a3Y3用来保证两种材料的收缩率接近。考虑双层注塑中，收缩率差异对翘曲、双层材料间结合性能的影响显著，所以 Y3对应的权重因子 a3取较大值，并参考文献[19-20]，其取值分别为0.1、0.1、0.8。由于评价分量均属于越小越优的指标，因此收缩的综合评价指标Y也为越小越优的指标。为对各变量进行分析，需确定优化设计中，变量的可行解空间，这需进行各变量对评价指标的影响研究。在双色变模温成型过程中，需要调节的工艺参数很多，由Kabanemi等[21]的研究可知，工艺参数对收缩的影响大小的前3位为保压压力、冷却时间、模具温度，本文对两种材料的保压压力（Pp）、冷却时间（tc）和模具温度（Tm）等6个变量进行分析，其范围选择为第1次充填期间(PC高光)Pp1为30～90 MPa，tc1为10～40 s，Tm1为125～150℃；第2次充填期间(ABS)Pp2为30～60 MPa，tc2为10～30 s，Tm2为60～80℃。

2.2 模拟试验

论文采用拉丁超立方抽样[22]的方法，对2.1节所述变量及范围内，取20组变量样本点（表1），利用 Moldflow分析软件对所取得的样本点进行模拟，模拟过程涉及的其他工艺参数如表2所示，模拟结果图5所示。

表1 拉丁超立方取样试验安排Table 1 Latin hypercube sampling for test arrangement

表2 其他工艺参数Table 2 Some other process parameters

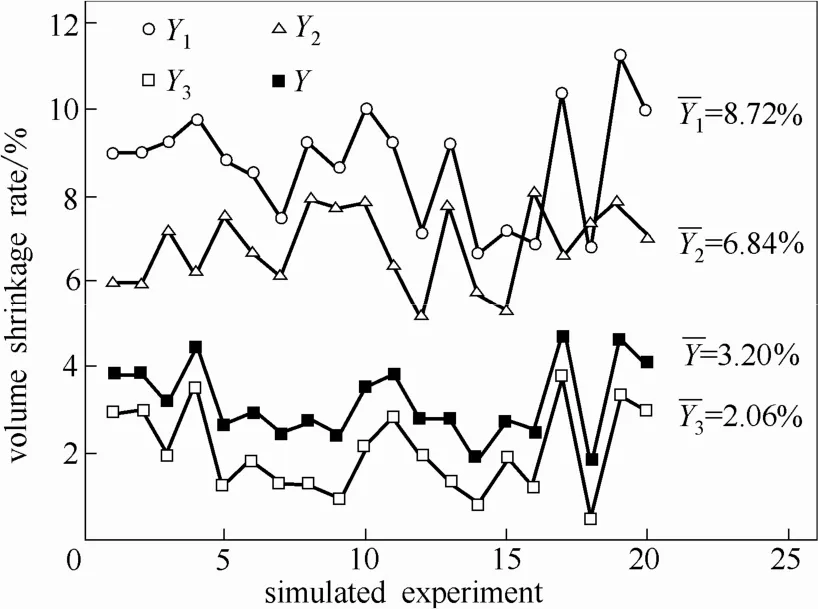
图5 试验的收缩率模拟结果Fig.5 Shrinkage of simulation test results

由图 5可知，收缩率的模拟结果为：① 两种材料的收缩率 Y1和 Y2的平均值分别为 8.72%和6.84%；② Y1明显高于Y2，其差的绝对值Y3最高趋近于4.00%，均值为2.06%；③ 综合评价指标最高为4.74%，均值为3.20%。由此可见，PC和ABS两种材料的收缩率Y1和Y2均较高，其差值Y3较大，而这3个指标对双层注塑产品的翘曲、结合强度低等问题的影响是显著的，因此，2.1节所述加权两种材料的收缩率及其差值的评价指标合理可行。

2.3 Kriging模型的建立与检验

2.3.1 Kriging模型的描述 Kriging代理模型[15-16]是一种基于统计的半参数化插值技术，其响应值Y为变量x的多项式f(x)与系统偏差μ(x)的和，表达式为

其中，a为回归系数，f(x)为零阶、一阶或二阶多项式，μ(x)为随机函数，它的统计均值为0，方差为，且对于任意两个样本点 w和 x有cov(μ(w), μ(x))=R(θ,w,x)，R(θ,w,x)为带参数θ的相关函数，表达式为

其中，Rj(θj, |wj−xj|)为相关函数的核函数，有多种表现形式，以让模型更具灵活性。

2.3.2 Kriging模型的建立与检验 论文利用Matlab中的 DACE工具箱[23]，选用式(4)所示高斯函数作为核函数，以拉丁超立方抽样的模拟试验的前17组数据进行Kriging近似模型的建立。

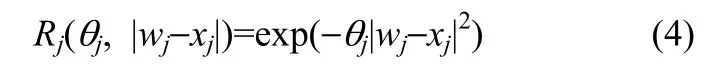
为检验模型的可靠性，论文利用拉丁超立方试验的后3组为输入，得出Kriging模型的综合质量指标响应值 Ykrig，与模拟结果的综合质量指标 Ysim进行对比检验，如图6所示。Ysim与Ykrig的两条曲线趋近，最大差值为0.36%，最小差值为0.07%，差值较小。因此，所建立的Kriging预测模型可靠。

图6 Kriging模型检验Fig.6 Verification of Kriging model

2.4 遗传算法的模型寻优

为对所建立的数学模型进行寻优，寻找最优评价指标及对应工艺参数组合，论文引入遗传算法及需要理论（GA理论[17-18]），以Kriging模型作为适应度函数，进行迭代寻优。种群设定为 100，交叉率为 0.5，变异率为 0.1，采用轮盘赌作为选择策略，迭代次数为100次，迭代寻优过程如图7所示，由图可知，适应度函数约80次迭代后收敛，求解得到的收缩综合评价指标值为0.7584%，小于前述所有试验结果值，对应的工艺参数取整后为：第1次充填期间(PC高光)Pp1为84 MPa，tc1为9 s，Tm1为128℃；第2次充填期间(ABS)Pp2为38 MPa，tc2为12 s，Tm2为55℃。

图7 遗传算法迭代寻优过程Fig.7 Iterative optimization process by GA

3 双层变模温成型收缩控制策略的结果与分析

为分析双层变模温成型收缩控制策略的可靠性，论文对上述优化结果进行了Moldflow模拟分析和生产验证。优化后顶出时体积收缩率模拟结果如图8所示，优化前后收缩结果对比如图9所示，分析可知，参数优化后遥控器前盖的成型收缩得到了明显控制，各项指标均大幅度下降，收缩综合评价指标为 0.7728%，小于前述所有试验的数值，接近Kriging模型的遗传算法预测值0.7584%，预测误差为0.0144%。模拟分析结果表明，提出的双层变模温成型收缩的控制策略可行。

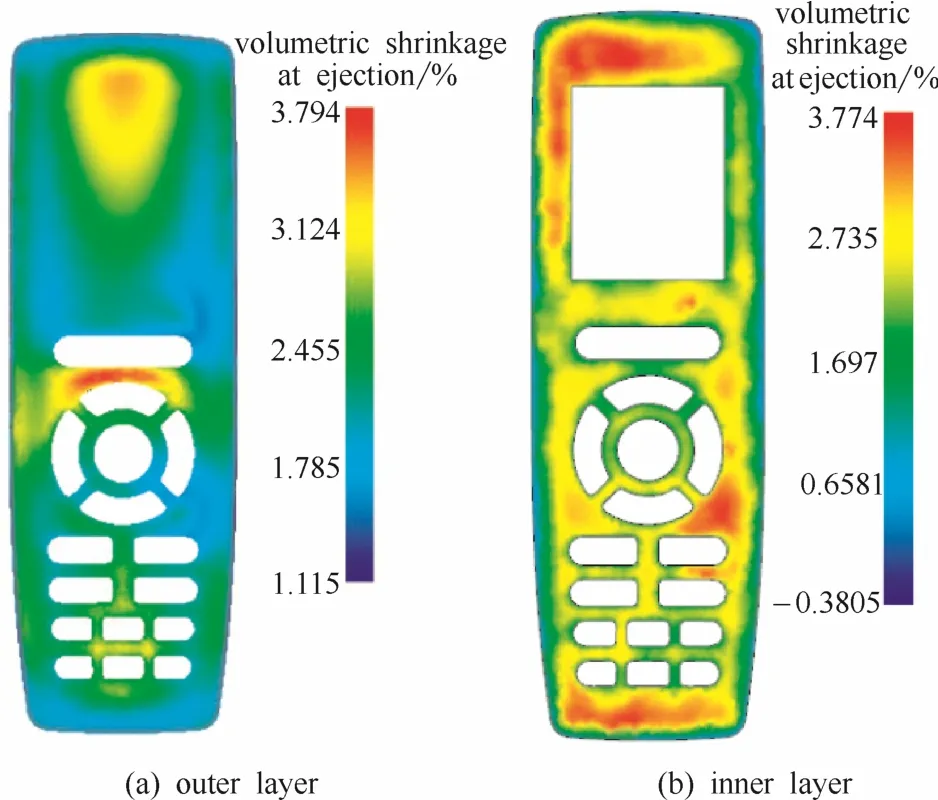
图8 优化后顶出时体积收缩Fig.8 Optimization volumetric shrinkage at ejection

图9 优化前后结果对比Fig.9 Shrinkage before and after optimization

生产试制的实物照片如图 10所示，遥控器前盖表面PC透明层呈现高光，无明显熔接痕，无明显收缩变形。图 11所示为优化前后材料结合处对比，由图可知，经控制策略获得的优化参数成型，PC与ABS两种材料的结合更好。因此，由生产试验结果得出本文针对遥控器前盖的双层变模温成型的收缩控制的研究方法可行。

图10 双层遥控器前盖生产实物照片Fig.10 Production of remote control's front cover

图11 优化前后结合处微观形貌对比Fig.11 Microstructure of interface before and after optimization

4 结 论

论文针对双层变模温的成型收缩问题，提出了一种结合Kriging代理模型和GA遗传算法的优化控制策略，主要结论如下。

（1）确定了基于顶出时体积收缩率的双层变模温的成型收缩评价体系。以遥控器前盖为例，通过初始模拟试验，寻找控制目标，即PC和ABS两次注射的顶出时体积收缩Y1、Y2及其绝对差值Y3，通过加权法得出成型收缩的综合评价指标Y。

（2）建立并检验了基于Kriging近似模型的控制变量与指标间数学关系。利用拉丁超立方抽样试验及结果进行 Kriging预测模型的建立和检验，检验结果Ykrig与模拟试验结果Ysim的两条曲线趋近，最大差值为0.36%，最小差值为0.07%，差值较小，Kriging模型可靠。

（3）进行了基于GA遗传算法的成型收缩工艺参数组合寻优。利用GA遗传算法，对Kriging模型进行迭代寻优，求解得到的收缩综合评价指标 Y为 0.7584%，变量分别为 Pp1=84 MPa，tc1=9 s，Tm1=128℃，Pp2=38 MPa，tc2=12 s，Tm2=55℃。

（4）实现了基于Kriging模型与GA遗传算法结合的双层变模温注射成型收缩控制策略，通过模拟及生产试验对策略的可行性进行验证，并对控制前后两层材料的结合处微观形貌进行分析，证明控制策略合理可行。

[1]DONDERO M, PASTOR J M, CARELLA J M, et al. Adhesion control for injection over molding of polypropylene with elastomeric ethylene copolymers[J]. Polymer Engineering & Science, 2009, 49(10): 1886-1893.

[2]ARZONDO L M, PINO N, CARELLA J M, et al. Sequential injection over molding of an elastomeric ethylene-octene copolymer on a polypropylene homopolymer core [J]. Polymer Engineering & Science, 2004, 44(11): 2110-2116.

[3]WANG G L, ZHAO G Q, LI H P, et al. Analysis of thermal cycling efficiency and optimal design of heating/cooling systems for rapid heat cycle injection molding process[J]. Materials & Design, 2010, 31(1): 3426-3441.

[4]NIAN S C, TSAI S W, HUANG M S, et al. Key parameters and optimal design of a single-layered induction coil for external rapid mold surface heating[J]. Int. Commun. Heat Mass, 2014, 57: 109-117.

[5]JIANG G J, ZHANG F S, WU H, et al. Comparative studies on enhanced interfacial adhesion between PE and PA6 through two routes in a sequential injection molding process[J]. Polymer-Plastics Technology & Engineering, 2014, 53(1): 9-18.

[6]NGUYEN S, PEREZ C J, DESIMONE M, et al. Adhesion control for injection over molding of elastomeric propylene copolymers on polypropylene. Effects of block and random microstructures[J]. International Journal of Adhesion & Adhesives, 2013, 46: 44-55.

[7]YAN B W, WU H, JIANG G J, et al. Interfacial crystalline structures in injection over-molded polypropylene and bond strength[J]. ACS Applied Materials & Interfaces, 2010, 2(11): 3023-3036.

[8]陈茂顺. 基于多浇口时序控制的双色高光注塑技术研究[D]. 南昌:南昌大学, 2012. CHEN M S. Research on high-gloss double-injection molding technology based on multi-gates sequence control [D]. Nanchang: Nanchang University, 2012.

[9]WANG G L, ZHAO G Q, LI H P, et al. Research of thermal response simulation and mold structure optimization for rapid heat cycle molding processes, respectively, with steam heating and electric heating[J]. Materials & Design, 2010, 31(7): 382-395.

[10]WANG G L, ZHAO G Q, WANG X X. Development and evaluation of a new rapid mold heating and cooling method for rapid heat cycle molding[J]. International Journal of Heat and Mass Transfer, 2014, 78: 99-111.

[11]XIAO C L, HUANG H X. Optimal design of heating system for rapid thermal cycling mold using particle swarm optimization and finite element method[J]. Applied Thermal Engineering, 2014, 64: 462-470.

[12]刘东雷, 申长雨, 刘春太, 等. 模具温度对高光注射成型制品表面沉降的影响[J]. 高分子材料科学与工程, 2012, 28(1): 168-171.LIU D L, SHEN C Y, LIU C T, et al. Influence of mold temperature on the sink mark of rapid heat cycle molding plastic part[J]. Polymer Materials Science and Engineering, 2012, 28(1): 168-171.

[13]刘东雷, 申长雨, 刘春太, 等. 基于响应曲面法与改进遗传算法的RHCM成型工艺优化[J]. 机械工程学报, 2011, 47(14): 54-61. LIU D L, SHEN C Y, LIU C T, et al. Efficient process parameters optimization of rapid heat cycling molding technology based on response surface methodology and improved genetic algorithm[J]. Journal of Mechanical Engineering, 2011, 47(14): 54-61.

[14]LUCCHETTA G, FIOROTTO M, BARIANI P. Influence of rapid mold temperature variation on surface topography replication and appearance of injection-molded parts[J]. CIRP Annals-Manufacturing Technology, 2012, 61(1): 539-542.

[15]高月华, 王希诚. 基于Kriging代理模型的稳健优化设计[J]. 化工学报, 2010, 61(3): 676-681. GAO Y H, WANG X C. Robust optimization based on Kriging surrogate model[J]. CIESC Journal, 2010, 61(3): 676-681.

[16]葛学伟, 韩先洪, 陈巍, 等. 基于 Kriging代理模型的气辅注射成型工艺优化[J]. 化工学报, 2010, 61(4): 909-915. GE X W, HAN X H, CHEN W, et al. Processing parameters optimization based on Kriging meta-model for gas-assisted injection molding[J]. CIESC Journal, 2010, 61(4): 909-915.

[17]KUSUM D, MANOJ T. A new crossover operator for real coded genetic algorithms[J]. Applied Mathematics and Computation, 2007, 188(1): 895-911.

[18]马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4): 1201-1206. MA Y J, YUN W X. Research progress of genetic algorithm [J]. Application Research of Computers, 2012, 29(4): 1201-1206.

[19]张小聪. BP神经网络与GA算法相结合的双色成型保压曲线优化[J]. 中国塑料, 2015, 29(1): 80-84. ZHANG X C. Optimization of pressure in bi-color molding through a hybrid of back propagation neural network and genetic algorithm [J]. China Plastics, 2015, 29(1): 80-84.

[20]杨海. 基于空调遥控器的双色高光蒸汽注塑技术研究[D].重庆：重庆大学, 2014. YANG H. Research on bi-color high-gloss injection molding technology based on air-condition remote control [D]. Chongqing: Chongqing University, 2014.

[21]KABANEMI K K, VALLANCOURT H, WANG H, et al. Residual stresses, shrinkage, and warpage of complex injection molded products: numerical simulation and experimental validation[J]. Polymer Engineering & Science, 1998, 38(1): 21-37.

[22]MCKAY M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 2000, 42(1): 55-61.

[23]SOREN N L, HANS B N, JACOB S. DACE a Matlab Kriging toolbox[DB/OL]. 2002[2005-02-19]. http:// www.imm.dtu.dk/～hbn/ dace/.

Strategy of molding shrinkage control for Bi-layered RHCM based on Kriging and GA

WANG Menghan, LIU Xiao, WEI Kang, LI Yanzhao
(College of Material Science and Engineering, Chongqing University, Chongqing 400030, China)

Due to high temperature and high pressure conditions of Bi-layered rapid heating cycle molding (Bi-layered RHCM), the molding shrinkage of its products is extremely sensitive to the change of process parameters, therefore, the key to improve quality of products is the strategy of molding shrinkage control. In order to explore and develop the strategy of molding shrinkage control, a remote control's front cover of air conditioner was an example for molding in this paper. Determined a multi-objective evaluation system and process parameters for measuring molding shrinkage. Latin Hypercube Sampling was used to design experiments, moreover, a numerical simulation software named Moldflow was used to simulate mold filling, pressure maintaining and cooling process to obtain test data. The mathematical relationship between parameters and evaluation index was estabilished by Kriging model. In order to find out the optimal evaluation index of molding shrinkage and corresponding process parameters, the mathematical relationship was iterative calculation by means of genetic algorithm (GA). Both simulation and production test were applied to verify the strategy of molding shrinkage control based on Kriging model combined with GA , and provide the reference of molding shrinkage control of Bi-layered RHCM.

Bi-layered RHCM; shrinkage control; Kriging model; genetic algorithm; numerical simulation

WANG Menghan, cquwmh@163. com

TQ 320.66

：A

：0438—1157（2017）01—0391—07

10.11949/j.issn.0438-1157.20160637

2016-05-09收到初稿，2016-10-14收到修改稿。

联系人及第一作者：王梦寒（1975—），女，博士，副教授。

中央高校基本科研业务费专项资金（CDJZR11130003）。

Received date: 2016-05-09.

Foundation item: supported by the Fundamental Research Funds for the Central Universities(CDJZR11130003).