基于微分代数积分矩量法的聚并器超细颗粒聚团研究

郑建祥，许帅，王京阳，史梦燚，汪龙

（东北电力大学能源与动力工程学院，吉林省 吉林市 132012）

基于微分代数积分矩量法的聚并器超细颗粒聚团研究

郑建祥，许帅，王京阳，史梦燚，汪龙

（东北电力大学能源与动力工程学院，吉林省 吉林市 132012）

研究聚并器内布朗聚团和湍流聚团引起超细颗粒聚团，特别考虑颗粒之间近程力（范德华引力、静电斥力）和颗粒与气体之间的流体力学作用力对颗粒聚团的影响。基于FLUENT软件UDF功能自定义聚团核，考虑颗粒之间近程力和流体力学作用力对聚并率的影响，引入碰撞效率α对聚团核进行修正，得到修正湍流聚并模型并将该模型与理想湍流聚并模型进行比较。应用群体平衡模型(population balance model，PBM)耦合CFD对颗粒聚团过程进行数值模拟，并采用微分代数积分矩量法(DAE-QMOM)求解群体平衡方程。结果表明：理想湍流聚并模型与实验结果误差为 8.92%，而修正改进的湍流聚团模型与实验结果误差仅为3.35%，更加符合实际情况；微分代数积分矩量法具有较高的效率，而且误差较小，相比PD积分矩量法有明显的优势，稳定性也比较突出。

超细颗粒物；湍流聚并器；群体平衡模型；颗粒聚团；聚并率；微分代数积分矩量法

引 言

目前燃煤电厂颗粒污染物控制的装置多为干式静电除尘器(ESP)[1]，静电除尘器对颗粒污染物除尘效率高达 99.5%以上，但是对于超细颗粒物的捕集效率相对较低[2]。燃煤飞灰中的超细颗粒数占总颗粒数的90%以上，超细颗粒排放进入大气会引起各种问题，特别是环境和健康问题[3]。在中国的大多数城市，颗粒物已经超过二氧化硫和氮氧化物成为主要的城市污染物。由于燃煤超细颗粒物所带来的严重危害，Yao等[4]对燃烧过程超细颗粒的形成与控制进行了基础研究，通过进行燃烧改造从而提高对可吸入颗粒排放控制技术，并详细介绍了增强袋式除尘效率和新型控制PM2.5的方法。

降低燃煤电厂超细颗粒排放的有效措施之一是在电除尘器或布袋除尘器之前通过物理或化学[5-7]作用提高亚微米级颗粒聚团，从而增加飞灰颗粒的尺寸达到提高超细颗粒捕集效率的目的。湍流聚并器由于其操作简单、投资少、运营成本低，在各种新技术中有更好的发展前景，聚并器是通过气流中颗粒之间的湍流而引起颗粒碰撞的增加，湍流导致颗粒相互之间速度的差异，提高颗粒间物理碰撞作用从而形成超细颗粒的聚团。已有许多研究[8-10]证明湍流聚团对细颗粒的捕集效果具有明显作用。

群体平衡模型更加适用于研究两相流中颗粒、液滴和气泡等聚并和破碎的变化过程。对于研究超细颗粒粒径聚团增长问题，McGraw[11]首次提出积分矩量法求解群体平衡方程，然而该方法假设积分点为正交的，为了克服这个封闭问题，McGraw采用Gordon[12]提出的Product-Difference(PD)算法。尽管PD积分矩量法(PD-QMOM)是一种有效的方法，但当研究高阶矩时该方法就失效了。Rong等[13]提出直接矩量法(DQMOM)，用于双内部坐标时此方法的优势是比较突出的。Gimbun等[14]运用联立颗粒聚团的群体平衡方程组方法，由矩定义的微分方程和由矩定义的约束限制组成。微分代数方程的半显式结果拥有比PD-QMOM更佳稳定性和计算效率，本文采用具有许多优势的微分代数积分矩量法(DAE-QMOM)求解群体平衡方程。

除了求解群体平衡方程的精确性，还有如何选择聚团核关系到数值模拟计算的准确性，因为颗粒聚团形成原因与方式以及颗粒之间相互作用对聚团的影响都包含在聚团核之中。Saffman等[15]和Wang等[16]直接忽略湍流聚团中颗粒之间的相互作用，得到理想的湍流聚团核。刘含笑等[17]运用适合任意密度颗粒聚团核对聚并器颗粒凝并过程模拟，并按湍动能值的不同定义聚团核分段函数。李云飞[18]对不同惯性颗粒聚并核分别进行定义，并根据颗粒特征长度与湍流特征长度的大小关系进行选择。以上所研究的聚团核存在一定的局限性，本文为了更加准确地评估湍流聚团，通过同时考虑颗粒动量、颗粒之间近程力（范德华引力、静电斥力）和流体与颗粒之间的流体动力学作用力对聚团的影响，引入颗粒碰撞效率α修正并改进了聚团核函数，使之更加接近实际情况，从而正确指导工程实际应用。

1 数值计算模型

1.1 气固两相流动模拟

采用Euler-Euler多相流模型用于研究颗粒与流体流动模拟，并且考虑了颗粒与流体之间的相互作用。湍流模型采用realizable k-ε模型[19]。

与标准k-ε模型相比，realizable k-ε模型引入了旋转、曲率相关项，避免出现负的正应力。本研究采用realizable k-ε模型对湍流流动进行模拟。

湍动能k和湍动能耗散率ε输运方程为

1.2 群体平衡模型

在欧拉框架下，表示多分散气溶胶粒度分布的变化的聚团群体平衡方程[20]为

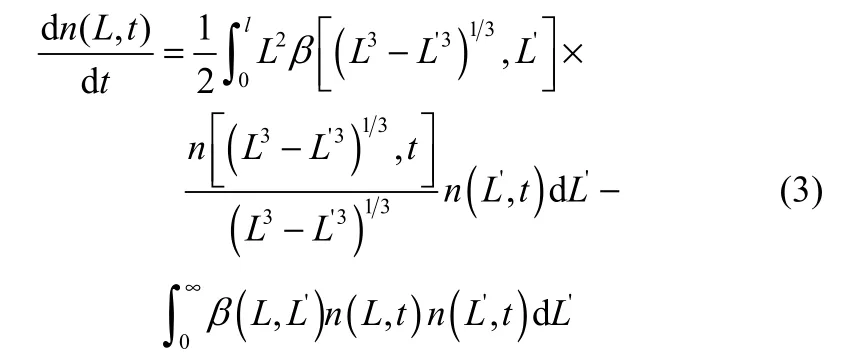
式中，L和L′表示内部坐标下的颗粒1和颗粒2的半径；n为颗粒的数密度；β(L,L′)为聚团核，m3·s−1。右边第1项是由于粒径为(L3−L′3)1/3的颗粒与粒径为L′的颗粒聚合形成粒径为L的颗粒聚团导致的粒径增长率。右边第2项是由于团聚引起的颗粒死亡率。

为了求解初始微分方程，McGraw[11]提出高斯积分方法应用于矩计算。

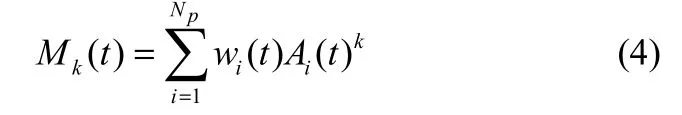
式中，Np为积分点；wi为权重；Ai为颗粒粒径分布积分近似的横坐标。应用矩的积分近似群体平衡方程的离散结果为

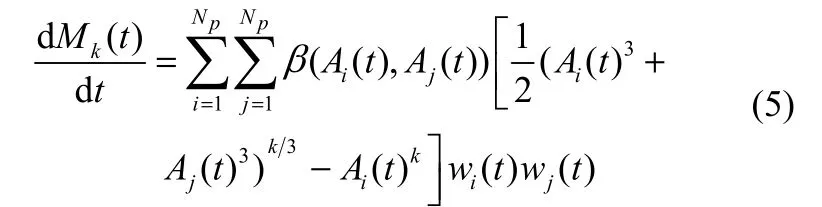
为了避免依赖于 PD算法或者 Wheeler[21]的算法去得到Mk、wi和Ai。Gimbun等[14]提出引入了在代数约束下微分方程组成的系统。微分代数方程一般简洁表达式为

F方程与式(5)相关被定义为

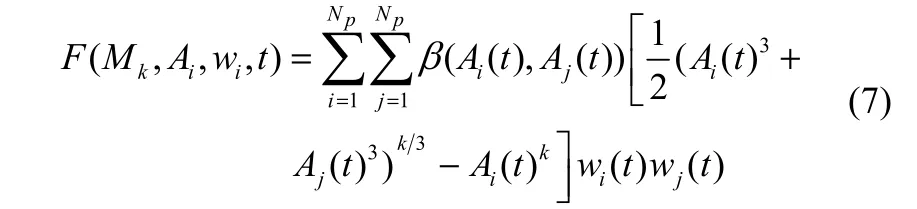
G方程与式(4)相关被定义为

1.3 DLVO理论

DLVO理论描述气溶胶颗粒之间的相互作用，对于在悬浮系统中具有相同表面张力ψ的不同颗粒，通常球形颗粒之间的静电排斥力采用Debye-Huckel[22]表达式如下

式中，λ为颗粒粒径之比；L为大颗粒的半径；ε为相对介电常数；s为两颗粒表面的量纲1长度；x为Debye-Huckel相关长度参数。

对于两个材料相同的球形颗粒的范德华引力近似为

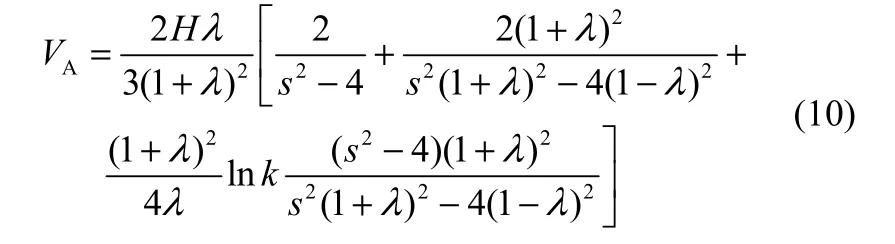
式中，H为Hamaker常数。

通常总的相互作用合力表示为能量势垒VT，VT是静电斥力VR与范德华引力VA之和，颗粒之间的相互作用力如图1所示。

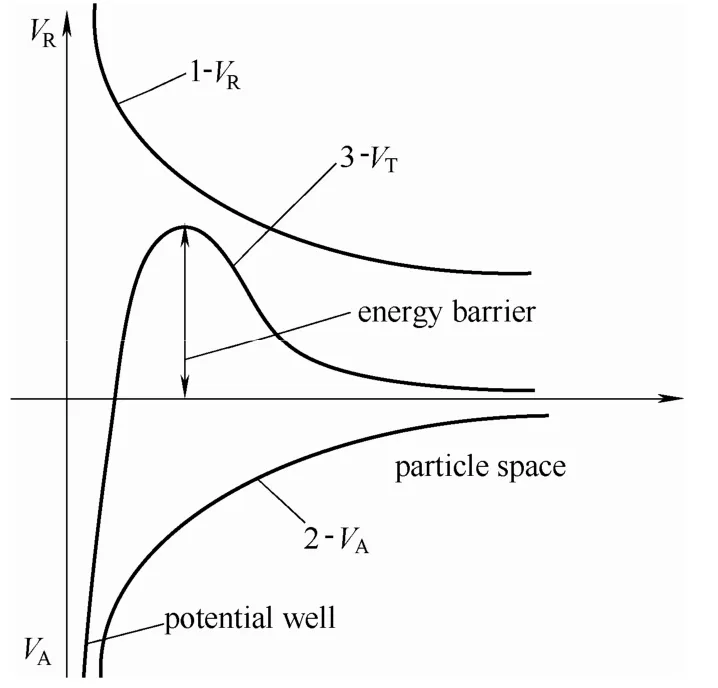
图1 DLVO理论图解Fig.1 Graphic theory of DLVO

从DLVO理论图解得到：只要克服了相互作用的能量势垒，颗粒之间距离变小，就能很容易地接触，进而发生碰撞导致聚团。

除了颗粒之间的近程力，流体与颗粒的流体力学作用力在颗粒实际碰撞过程中影响也比较大。当两个颗粒相互靠近，颗粒之间的距离逐渐缩小从而导致颗粒间的流体被挤压出去，流体的这种运动使得两个颗粒之间发生旋转运动，导致两个颗粒之间的运动轨迹发生偏转，偏移原来的路径，最终的结果就是碰撞频率减小从而导致颗粒聚团效果减小，所以流体力学作用力对颗粒碰撞的影响必须考虑。Fuchs[23]首次定义计算碰撞效率α的方法，将α的倒数定义为稳定系数W，即W=1/α，然后通过求解稳定系数W得到α的值，这种方法被研究者广泛应用。该方法在求解过程中只考虑了颗粒之间近程力的作用而忽略了流体力学作用力对颗粒碰撞的影响。Han等[24]在布朗聚团中考虑了颗粒与流体之间的流体力学作用力对聚团的影响，Chun等[25]在湍流聚团中得到流体力学作用力对颗粒聚团的影响比较大，并得到考虑该因素的碰撞效率α。本研究充分考虑近程力和流体力学作用力对聚并器湍流聚团的影响，通过碰撞效率进行修正，得到修正的湍流聚团模型。

1.4 聚团理论

颗粒聚团包含两个重要的过程。首先驱动力缩近颗粒之间的距离使颗粒聚集，以便颗粒之间发生碰撞；然后颗粒之间的作用力克服流体力学作用力最终形成聚团。通常，颗粒之间碰撞驱动力根据颗粒粒径确定，对于颗粒半径为1～10 μm之间的颗粒的驱动力为湍流运动，小于1 μm的颗粒的驱动力为布朗运动，大于10 μm的颗粒的驱动力为差速沉降。

在湍流聚并器内聚团的主要形式包括热聚团、库仑聚团、布朗聚团和湍流聚团，由于热聚团在整个聚团过程之中具有较小的影响，可以被忽略。除此之外，在本研究中假设颗粒为电中性，所以库仑聚团也是不考虑的。

1.4.1 布朗聚团 对于布朗聚团，存在一个至关重要的量纲1常数Kn，Kn是气体分子自由程与颗粒半径的比值。根据Kn的值，可以将颗粒区域分为4个区域：连续区(Kn≤0.1)，滑动区(0.1≤Kn≤1)，过渡区(1＜Kn≤10)，以及自由分子区(Kn＞10)。本研究中超细颗粒是直径变化在0.02～10 μm，所以经计算得到颗粒可以视为自由分子区。在这种情况下，布朗聚团核为

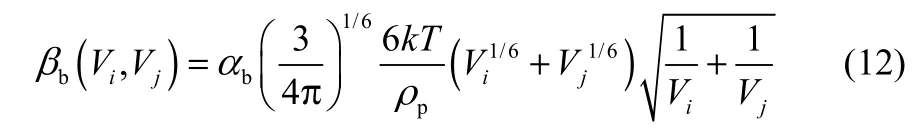
式中，αb为布朗聚团考虑颗粒之间近程力与流体力学作用力对颗粒碰撞影响的碰撞效率；k是Boltzmann常数，k=1.381×10−23；T为热力学温度，T=293.15 K； Vi和Vj分别为颗粒i和颗粒j所对应的体积。

αb通过求解包括流体力学作用力和颗粒间作用力的分散方程得到

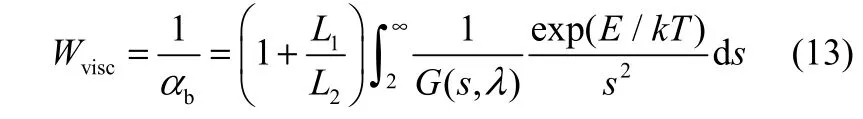
式中，L1和 L2分别表示大颗粒和小颗粒的半径；G(s,λ)为流体动力学方程；s为两颗粒表面的量纲1长度；λ表示小颗粒与大颗粒粒径之比；E是颗粒之间的能量。

1.4.2 湍流聚团 对于湍流聚团，St表示颗粒弛豫时间尺度和流体特征时间尺度之比。根据St的值，颗粒类型可以分为3种类型：零惯性颗粒(St→0)、有限惯性颗粒和极大惯性颗粒(St→∞)。

（1）零惯性颗粒。零惯性颗粒的湍流聚团通常适用于颗粒半径为2～5 μm。根据Saffman等[15]所提出的不考虑颗粒之间的相互作用力下理想聚团核为

式中，ε为单位质量流体的能量耗散率，m2·s−3；ν为流体的运动黏性系数，m2·s−1；Li和Lj分别是颗粒i和颗粒j所对应的直径。

（2）有限惯性颗粒。对于粒径在1～10 μm范围内的颗粒，其黏性弛豫时间τv小于1.2×10−3s，湍流剪切对颗粒聚团起决定性作用。该范围内的颗粒由湍流剪切引起的聚并率比差速沉降和湍流加速度引起的聚并率高。对于这个粒径范围颗粒和适中大小的 Kolmogorov剪切率，颗粒动量显著提高聚团作用。

颗粒动量影响增加在中间长度尺度的颗粒对概率和颗粒的局部相互作用，可以得到理想聚并率的修正形式，考虑动量、颗粒之间近程力与流体力学作用力对颗粒聚团影响引入修正系数αt对聚并率修正得到修正湍流聚团核为

αt表示湍流聚团考虑颗粒之间近程力与流体力学作用力对颗粒碰撞影响的碰撞效率。

式中，Rhit和 Rtrail分别为颗粒碰撞对数与所有的颗粒数；U为颗粒对的相对速度；c0为高斯颗粒分布修正因素；L为颗粒直径。

（3）极大惯性颗粒。对于极大惯性颗粒采用Abrahamson[26]提出的聚团核模型为

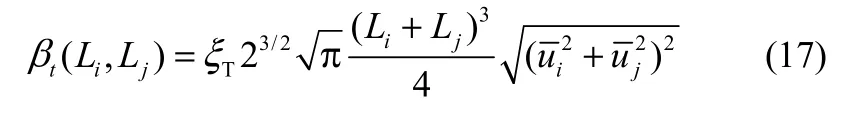
由于布朗聚团和湍流聚团对于不同颗粒碰撞聚团有不同的作用，所以聚团核可以假设各自相互独立[27]，所以本研究的聚团核可以定义为

式中，下角标b和t分别代表布朗聚团和湍流聚团。

2 数值模拟

2.1 物理模型

湍流聚并器主要由导流叶片和涡流发生器组成，分为导流段和混合段两部分。聚并器的长和宽分别为1500 mm和600 mm。导流叶片和涡流发生器之间相距190 mm，壁面距涡流发生器130 mm，两个相邻涡流发生器行列间距分别为 150 mm和170 mm。聚并器具体形状和尺寸如图2所示。

2.2 边界条件的设定

聚并器入口边界条件设置速度入口，入口气体速度 Vin=15 m·s−1，连续相介质为空气，密度为0.795 kg·m−3，黏度为2.3×10−5kg·(m·s)−1。颗粒相密度为2100 kg·m−3，粒径分布为0.2～12 μm。出口边界条件设置为自由出口，并且出口处的流动状态为充分发展状态，墙壁为无滑移边界条件，PC-SIMPLEC算法用于进行速度压力耦合。PBE方程采用DAE-QMOM算法，聚团核函数通过UDF自定义编程，动量、湍动能和湍流耗散率为二阶迎风离散格式，收敛精度设为 10−5，时间步长为0.0001 s。

图2 聚并器结构Fig.2 Aggregation device structure

3 模拟结果与分析

3.1 PD-QMOM、DAE-QMOM和分区法比较

对聚并器内颗粒聚团过程分别采用PD-QMOM、DAE-QMOM和分区算法进行模拟计算，将计算所得的结果与解析解进行对比分析，从而评价三者的计算精度与效率。三种算法的误差随聚并器内超细颗粒聚团进行时间t变化的趋势如图3所示。其中，分组法采用最小和最大颗粒粒径分别为0.1 μm和10 μm，分组数为200。从图中可以看出，在颗粒聚团初期三者的误差大小基本一致，然而随着颗粒聚团过程的进行，分组法相较于两个矩方法的误差较大，而且呈现随时间的增大而波动较大的趋势。PD-QMOM算法与DAE-QMOM算法都具有较高的效率，然而 DAE-QMOM算法误差较小具有更加明显的优势，稳定性也比较突出，所以综合三者比较DAE-QMOM算法更加适合对于超细颗粒聚团的研究。

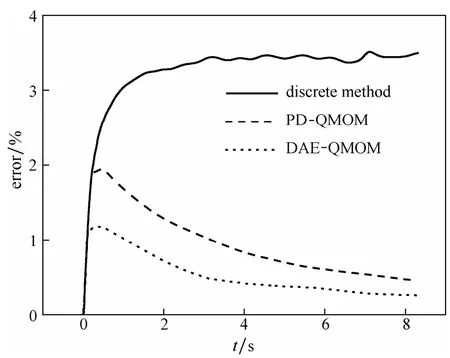
图3 PD-QMOM算法、DAE-QMOM算法和分区法精度比较Fig.3 Calculation comparison of PD-QMOM, DAE-QMOM and discrete method

3.2 数值模拟结果和实验验证

对超细颗粒聚团模拟采用三阶的DAE-QMOM方法，可以得到0～5阶矩量的变化。图4中可以看出，在湍流聚并作用下超细颗粒总浓度（m0）随着时间的变化持续减小，说明颗粒之间由于发生聚团作用导致小颗粒数密度减小，飞灰中超细颗粒与大颗粒碰撞聚团，从而导致超细颗粒数量减小。同样降低的还有颗粒总特征长度（m1）和颗粒总面积（m2），从图还可以得到超细颗粒总体积（m3）随着时间的变化保持恒定不变，这说明小颗粒与大颗粒碰撞之后形成新的颗粒，虽然数密度发生变化，但是聚团之后的颗粒总体积没有发生改变，这说明了数值模拟计算的正确性。除此之外，高于3阶的矩量变化趋势为随着时间的增大而变大。

图5为湍流聚团中的Sauter平均直径随时间的变化，从图中可以得出Sauter平均直径随时间的增加而增大，这说明颗粒之间发生聚团之后使得聚并器内的颗粒平均直径变大。由Sauter平均直径变化曲线斜率可知，颗粒的增长率慢慢减小，这是因为湍流聚并器内颗粒聚团作用随时间的增加而不断减弱，颗粒聚团效果趋于稳定。

为了验证基于DAE-QMOM的聚并器超细颗粒湍流团聚数值模拟的准确性，将数值模拟所得结果与实验结果进行对比，实验所采用的设备和方法采用文献[28]。实验所采用的烟气浓度在 22～25 g·m−3，烟气中的燃煤飞灰的初始粒径如图6所示，基本满足对数正态分布。图7为燃煤超细颗粒浓度在聚并器作用下的变化。从图7中可以看出，实验所得结果与数值模拟计算的结果较为符合，其变化规律也基本一致，验证了聚并器湍流聚团的计算模型和方法的准确性。

3.3 颗粒之间近程力和流体力学作用力对湍流聚团核的影响

在聚并器湍流聚团中，决定颗粒团聚效果的最终参数是团聚核函数。传统的理论模型过于简化，忽略了颗粒之间的近程力（静电斥力、范德华引力）和颗粒与流体之间的流体力学作用力，图8～图10分别为考虑颗粒之间近程力影响修正聚团核、考虑颗粒流体之间流体力学作用力影响修正聚团核和考虑两者因素影响修正聚团核与理想聚团核之间的比较。从图中可以看出，考虑近程力和流体力学作用力修正对聚团核影响较大，经过修正后的聚团核函数均比修正前小，尤其是颗粒粒径在 PM2.5范围内的降幅很大，可见理想的湍流聚团模型过高地估计了这个粒径范围内的颗粒团聚效果。对聚并器湍流聚团研究主要针对于 PM2.5超细颗粒污染物控制。通过以上分析，颗粒在 PM2.5范围内的碰撞效率较低，对湍流聚团影响重大，所以必须考虑近程力和流体力学作用力对湍流聚团的影响，通过对比分析得到更加适合聚并器湍流聚团模型。

图4 湍流聚团中超细颗粒各阶矩的变化Fig.4 Change of moments in turbulent aggregation

3.4 理想湍流聚并模型计算结果、修正湍流聚并模型计算结果和实验结果三者对比

图 11是采用理想湍流聚并模型计算结果、修正湍流聚并模型计算结果和实验结果[28]的对比。从该图中可以看出，与聚并器进口颗粒粒径分布相比较，小颗粒数量明显减少，大颗粒数量显著增大。这是由于飞灰颗粒经过湍流聚并器时，飞灰颗粒中的超细颗粒发生湍流聚团和布朗聚团作用，导致小颗粒与大颗粒碰撞聚团从而形成更大粒径的颗粒，所以在聚并器的出口小颗粒的数量减少。具体表明，颗粒粒径小于 1.8 μm的颗粒消除效率很低，从图11中可以看出小于1.8 μm的颗粒数目略有增加，这是由于燃煤超细颗粒中小于1.8 μm和亚微米颗粒数量基数非常庞大，其参与颗粒碰撞聚团的数量较少，而总颗粒数量却降低，所以小于1 . 8 μ m的颗粒数量比例增加。颗粒粒径在1 . 8～8 . 2 μ m之间的颗粒体积分数明显减少，新产生的大于1 0 μ m的颗粒体积分数增大。虽然理想湍流聚并模型计算结果与实验结果的趋势基本一致，但计算结果明显高于实验结果，两者的误差达到8 . 9 2 %。分析其原因为理想湍流聚并模型假设只要两个颗粒之间发生碰撞就会导致颗粒聚团，而忽略了颗粒之间的近程力（范德华引力、静电斥力）对颗粒聚团的影响，然而往往颗粒之间的进程力决定了相互碰撞的颗粒是否可以发生聚团而得到新的颗粒。也没有考虑流体力学作用力对颗粒聚团的影响，流体力学作用力在实际碰撞中影响作用比较明显。因为在颗粒碰撞的过程中，当两个颗粒相互靠近，颗粒之间的距离逐渐缩小从而导致颗粒间的流体被挤压出去，流体的这种运动使得两个颗粒之间发生旋转运动导致两颗粒之间的运动轨迹发生偏转并偏移原来的路径，最终的结果就是碰撞频率减小从而颗粒聚团效果减小。所以以上的颗粒之间的范德华引力、静电斥力、流体力学作用力对颗粒聚团影响不容忽视。

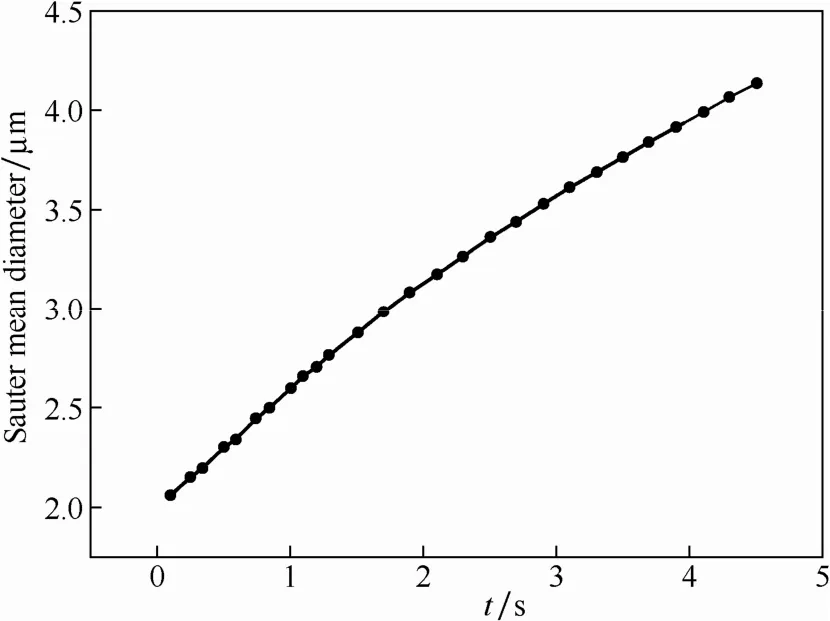
图5 湍流聚团中超细颗粒Sauter平均直径的变化Fig.5 Change of Sauter mean diameter in turbulent aggregation

图6 初始颗粒粒径分布Fig.6 Initial particle size distribution

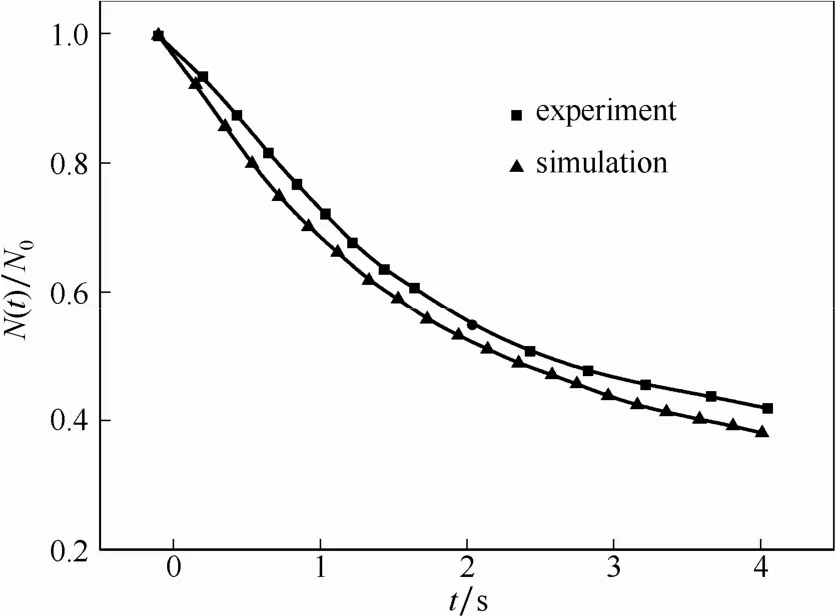
图7 燃煤飞灰烟气浓度变化实验与数值模拟结果比较Fig.7 Comparison of experimental concentration and numerical simulation concentration of coal-fired fly ash

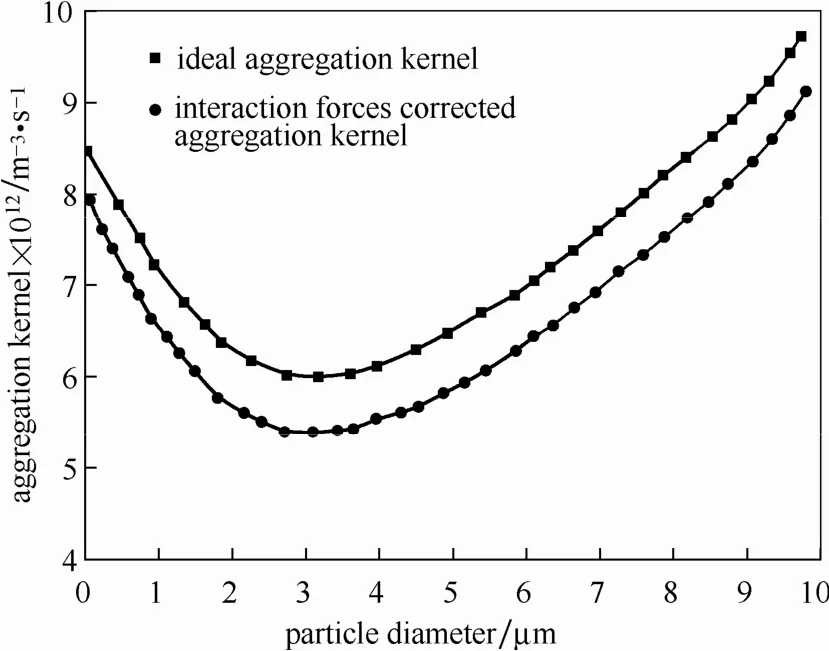
图8 考虑近程力修正聚团核与理想聚团核比较Fig.8 Comparison of corrected aggregation kernel by interparticle forces and ideal aggregation kernel

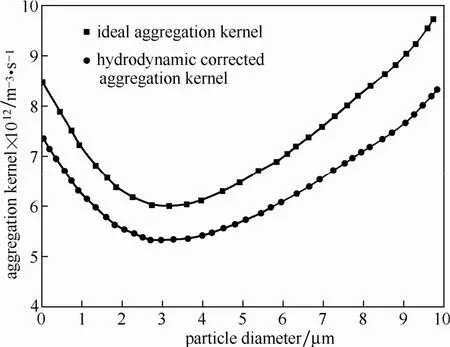
图9 考虑流体力学作用力修正聚团核与理想聚团核比较Fig.9 Comparison of corrected aggregation kernel by hydrodynamic and ideal aggregation kernel

图10 考虑近程力和流体力学作用力修正聚团核与理想聚团核比较Fig.10 Comparison of corrected aggregation kernel by interparticle forces and hydrodynamic and ideal aggregation kernel

图11 理想湍流聚并和修正湍流聚并粒径分布Fig.11 Particle size distribution of ideal and the corrected turbulence aggregation

表1更加直观地对比了理想湍流聚并模型计算结果、修正湍流聚并模型计算结果和实验结果下各个粒径区间内颗粒体积分数的变化。

修正湍流聚团模型计算结果与实验结果基本吻合。在实际中，颗粒碰撞和颗粒粒径的变化不仅仅由流体流动和颗粒动量控制，也受局部的颗粒与流体之间和颗粒与颗粒之间的相互作用。湍流剪切运动使两个颗粒发生碰撞叫做几何碰撞。然而这两个颗粒是团聚成一个大的颗粒还是相互弹开，这就依赖流体与颗粒和颗粒与颗粒之间的相互作用力。考虑颗粒与流体之间的流体作用力和颗粒与颗粒之间的范德华引力和静电斥力对颗粒聚团的影响，得到碰撞效率对聚并率进行修正，使聚团模型更加符合实际情况。由图可知，实验和加载修正湍流聚并核聚团模拟条件下所得小于 2.5 μm颗粒体积比例减小分别为80.9%和81.9%，2.5～5 μm颗粒体积比例减小分别为85.3%和86.6%，5～10 μm颗粒体积比例减小分别为71.5%和 73.7%。与实验结果相比理想湍流聚并模型的误差在8.92%左右，而修正湍流聚并模型误差仅有3.35%，修正湍流聚并模型与实验结果比较一致。其原因为理想湍流聚并模型为了简化计算假设整个体系的碰撞效率α为1，过高地估计了颗粒的聚团效果，造成了较大的误差。修正湍流聚并模型引入碰撞效率α对聚团核进行修正，分析了近程力与流体动力学作用力对颗粒聚团的影响，得到更加适合湍流聚并器聚团模拟的聚团核，模拟所造成的误差较低，得到的结果更加接近实际情况。

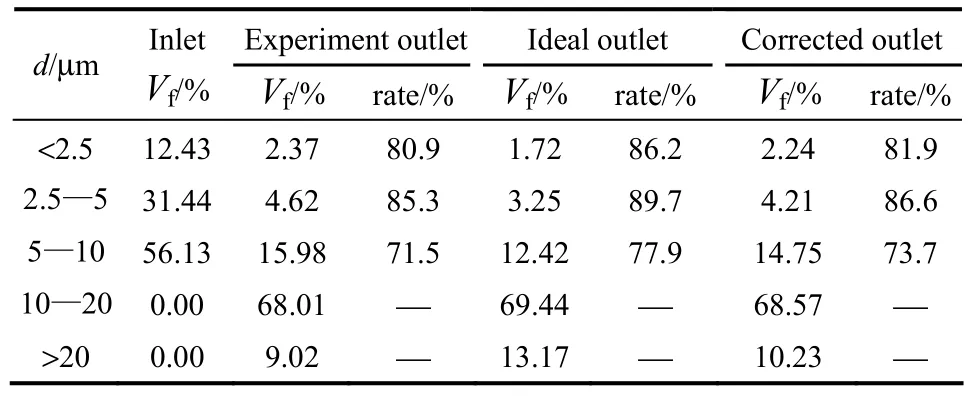
表1 各个粒径区间内颗粒体积分数的变化Table 1 Change of volume fraction of particles in different size range

4 结 论

本文采用 PBM耦合不同聚团核模型对聚并器内颗粒聚团过程进行模拟研究，主要分析了理想湍流聚团和修正湍流聚团之间的不同，得到如下结论。

（1）DAE-QMOM算法具有较高的效率，而且DAE-QMOM算法误差较小具有更加明显的优势，稳定性也比较突出。

（2）充分考虑颗粒之间范德华引力与静电斥力和流体力学作用力对聚并率的影响，引入碰撞效率α对聚团核进行修正得到修正湍流聚并模型。

（3）通过对理想湍流聚并模型和修正湍流聚并模型与实验结果的对比，理想湍流聚并模型的误差在8.92%左右，而修正湍流聚并模型误差仅有3.35%，修正湍流聚并模型与实验结果比较一致。

符 号 说 明

Ai——颗粒粒径分布积分近似的横坐标

L ——颗粒半径，μm

m0——颗粒数目总浓度

m1——颗粒粒径之和

m2——颗粒总表面积

m3——颗粒总体积

nk——颗粒数密度

St——斯托克斯数

T ——热力学温度，K

VA——范德华引力

Vf——体积分数

Vin——入口速度，m·s−1

VR——静电斥力

wi——积分权重

α ——碰撞效率

βb——布朗聚团核，m3·s−1

βt——湍流聚团核，m3·s−1

ε ——流体的能量耗散率，m2·s−3

ν ——流体的运动黏性系数，m2·s−1

[1]龙正伟, 冯壮波, 姚强. 静电除尘器数值模拟[J]. 化工学报, 2012, 63(11): 3393-3401. LONG Z W, FENG Z B, YAO Q. Numerical modeling of electrostatic precipitator[J]. CIESC Journal, 2012, 63(11): 3393-3401.

[2]熊桂龙, 李水清, 陈晟, 等. 增强PM_(2.5)脱除的新型电除尘技术的发展[J]. 中国电机工程学报, 2015, 35(9): 2217-2223. XIONG G L, LI S Q, CHEN S, et al. Development of advanced electrostatic precipitation technologies for reducing PM2.5 emissions from coal-fired power plants[J]. Proceedings of the CSEE, 2015, 35(9): 2217-2223.

[3]隋建才, 徐明厚, 丘纪华, 等. 燃煤可吸入颗粒的物理化学特性及形成机理[J]. 化工学报, 2006, 57(7): 1664-1670. SUI J C, XU M H, QIU J H, et al. Physical and chemical properties and formation mechanism of inhaled particles produced by coal combustion[J]. Journal of Chemical Industry and Englineering(China), 2006, 57(7): 1664-1670.

[4]YAO Q, LI S Q, XU H W, et al. Studies on formation and control of combustion particulate matter in China: a review[J]. Energy, 2010, 35(11): 4480-4493.

[5]颜金培, 陈立奇, 杨林军. 燃煤细颗粒在过饱和氛围下声波团聚脱除的实验研究[J]. 化工学报, 2014, 65(8): 3243-3249. YAN J P, CHEN L Q, YANG L J. Agglomeration removal of fine particles at super-saturation steam by using acoustic wave[J]. CIESC Journal, 2014, 65(8): 3243-3294.

[6]洪亮, 王礼鹏, 祁慧,等. 细颗粒物团聚性能实验研究[J]. 热力发电, 2014, 43(9): 124-128. HONNG L, WANG L P, QI H, el al. Experimental research on agglomeration characteristics of fine particlulate matters in Shajiao C Power Plant[J]. Thermal Power Generation, 2014, 43(9): 124-128.

[7]TRUCE R, CRYNACK R, WILKINS J, 等. INDIGO凝聚器——减少电除尘器可见排放物的有效技术[C]//第 11届全国电除尘学术会议论文集. 2005: 244-252. TRUCE R, CRYNACK R, WILKINS J, et al. The indigo agglomerator: the effective technology to reduce ESP visible emissions[C]//Proceedings of the 11th Conference of ESP. 2005: 244-252.

[8]LI Y F, YANG J G, WANG Y Y, et al. A novel turbulent aggregation device for flue gas[C]//Advanced Materials Research. Trans Tech Publications, 2014, 955: 2425-2429.

[9]郑建祥, 朱秀丽. 粘附性颗粒流化特性研究及信息熵分析[J]. 东北电力大学学报, 2015, 35(2): 18-22. ZHENG J X, ZHU X L. Study and application of shannon entropy in analysis of flow behavior of cohesive particle agglomerations[J]. Journal of Northeast Dianli University, 2015, 35(2): 18-22.

[10]刘忠, 刘含笑, 冯新新,等. 湍流聚并器流场和颗粒运动轨迹模拟[J]. 中国电机工程学报, 2012, 32(14):71-75. LIU Z, LIU H X, FENG X X, et al. Simulation for the flow field of the turbulence coalescence device and the trajectory of particles[J]. Proceedings of the CSEE, 2012, 32(14): 71-75.

[11]MCGRAW R. Description of aerosol dynamics by the quadrature method of moments[J]. Aerosol Science & Technology, 2007, 27(2): 255-265.

[12]GORDON R G. Error bounds in equilibrium statistical mechanics[J]. Journal of Mathematical Physics, 1968, 9(5): 655-663.

[13]RONG F, MARCHISIO D L, FOX R O. Application of the direct quadrature method of moments to polydisperse gas-solid fluidized beds[J]. Powder Technology, 2004, 139(1): 7-20.

[14]GIMBUN J, NAGY Z K，RIELLY C D. Simultaneous quadrature method of moments for the solution of population balance equations, using a differential algebraic equation framework[J]. Industrial & Engineering Chemistry Research, 2009, 3(1): 23-28.

[15]SAFFMAN P G, TURNER J S. On the collision of drops in turbulent clouds[J]. Journal of Fluid Mechanics, 1956, 1(1): 16-30.

[16]ZHOU Y, WEXLER A S, WANG L P. On the collision rate of small particles in isotropic turbulence(Ⅱ): Finite inertia case[J]. Physics of Fluids, 1998, 10(5): 1206-1216.

[17]刘含笑, 姚宇平, 郦建国. 凝聚器二维单扰流柱流场中颗粒凝并模拟[J]. 动力工程学报, 2015, 4(5): 292-297. LIU H X, YAO Y P, LI J G. Coagulating simulation of particles in flow field of coagulator 2D single turbulence column[J]. Journal of Chinese Society of Power Engineering, 2015, 4(5): 292-297.

[18]李云飞. 煤烟气细颗粒物湍流团聚的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. LI Y F. Research on turbulent aggegation of fine particles in flue gas[D]. Harbin: Harbin Institute of Technology, 2014.

[19]陈阿强, 王振波, 孙治谦. 基于相群平衡模型的浮选气泡聚并模拟[J]. 化工学报, 2015, 66(12): 4780-4787. CHEN A Q, WANG Z B, SUN Z Q. Numerical simulayion of bubble coalescence in dissolved air flotation tank based on population balance model[J]. CIESC Journal, 2015, 66(12): 4780-4787.

[20]MEYER C J, DEGLON D A. Particle collision modeling—a review[J]. Minerals Engineering, 2011, 24(8): 719-730.

[21]CHENG J C, VIGIL R D, FOX R O. A competitive aggregation model for Flash NanoPrecipitation[J]. Journal of Colloid & Interface Science, 2010, 35(2): 330-342.

[22]HOGG R, HEALY T W, FUERSTENAU D W. Mutual coagulation ofcolloidal dispersions[J]. Trans. Faraday Soc., 1966, 62(3): 1638-1651.

[23]FUCHS N. Uber die stabilitat and aufladung der aerosole[J]. Zeitschrift fur Physik, 1934, 89(11):736-743.

[24]HAN M Y, LEE H. Collision effiency factor in Brownian cogulation for unstable and stable suspension including hydrodynamics and interparticle forces[J]. KSCE Journal of Civil Engineering, 1997, 1(1):95-102

[25]CHUN J, KOCH D L. Coagulation of monodisperse aerosol particles by isotropic turbulence[J]. Physics of Fluids, 2005, 17(17):779-797.

[26]ABRAHAMSON J. Collision rates of small particles in a vigorously turbulent fluid[J]. Chemical Engineering Science, 1975, 30(11): 1371-1379.

[27]ZAICHIK L I, SOLOVEV A L. Collision and coagulation nuclei under conditions of brownian and turbulent motion of aerosol particles[J]. High Temperature, 2002, 40(3):422-427.

[28]章鹏飞, 米建春, 潘祖明. 装置元件排列间距和颗粒浓度对细颗粒湍流聚并的影响[J]. 中国电机工程学报, 2016, 36(6): 1625-1632. ZHANG P F，MI J C, PAN Z M. Influences of elemental arrangement and particle concentration on fine particle amalgamation[J]. Proceedings of the CSEE, 2016, 36(6): 1625-1632.

Simulation of ultrafine particle aggregation in aggregation device by differential-algebraic quadrature method of moments

ZHENG Jianxiang, XU Shuai,WANG Jingyang, SHI Mengyi, WANG Long
(School of Energy and Power Engineering, Northeast Electric Power University, Jilin 132012, Jilin, China)

The ultrafine particle aggregation arising from Brownian aggregation and Turbulence aggregation in turbulence aggregation device was studied, especially influences of short range force (van der Walls attraction and electric repulsion) among particles and hydrodynamics between particle and gas upon particle aggregation. Based on user-defined aggregation kernel of UDF function of FLUENT software, influences of short range force and hydromechanics among particles upon aggregation rate were studied and aggregation kernel was corrected using collision efficiencyα. Then, a corrected turbulence aggregation model was established and was compared with an ideal turbulence aggregation model. Particle aggregation process underwent numerical simulation using population balance model (PBM) coupling CFD and population balance equation was solved using differential-algebraic framework (DAE-QMOM). The results showed an error of 8.92% between the ideal turbulence aggregation model and the experimental result and an error of 3.35% between the corrected turbulence aggregation model and the experimental result, the latter conformed to practical situations better. Differential-algebraic quadrature method of moment as a high efficiency, a small error rate and a high reliability, it has obvious advantages over PD quadrature method of moment.

ultrafine particle; turbulence aggregation device; population balance model; particle aggregation; aggregation rate; differential-algebraic framework quadrature method of moments

Prof. ZHENG Jianxiang, 59745289@qq.com

TK 124

：A

：0438—1157（2017）01—0119—10

10.11949/j.issn.0438-1157.20160874

2016-06-27收到初稿，2016-10-20收到修改稿。

联系人及第一作者：郑建祥（1977—），男，博士，副教授。

吉林省教育厅“十三五”科研项目(［2016］第81号)；吉林市科技发展项目(20156405)。

Received date: 2016-06-27.

Foundation item: supported by the 13th Five-year Research Program of Jilin Province Education Department ([2016]No.81) and the Science and Technology Development of Jilin(20156405).