离子对CO2-盐水系统界面特性的影响

季佳圆，赵伶玲，李偲宇

（东南大学能源与环境学院，能源热转换及其过程测控教育部重点实验室，江苏 南京 210096）

离子对CO2-盐水系统界面特性的影响

季佳圆，赵伶玲，李偲宇

（东南大学能源与环境学院，能源热转换及其过程测控教育部重点实验室，江苏 南京 210096）

应用分子动力学模拟的方法对不同浓度及组分比例的 CO2-NaCl、CO2-CaCl2和 CO2-(NaCl+CaCl2)等 CO2-盐水系统的界面张力进行了研究，从分子层面上分析了不同种类的盐离子对界面张力的影响。结果表明，盐离子的存在会增加CO2-纯水的界面张力，界面张力增量主要由阳离子电荷数导致，其余则由阳离子兰纳-琼斯势参数、原子质量等原子特性参数引起；3种系统的界面张力增量均与离子强度呈线性关系，且其曲线的斜率和盐溶液种类无关，为IFT预测提供理论指导。

CO2-盐水系统；界面张力；分子模拟；原子特性参数；离子强度

引 言

深部盐水层分布广泛、存储容量大，因此被作为CO2地质封存的储存选址而备受推崇[1-2]。在CO2注入深部盐水层时，流体之间的界面张力（interfacial tension，IFT）直接决定了封存安全性、注入能耗及最大存储量，因此研究CO2与盐水之间的界面相互作用及界面性质具有重大意义。

深部盐水层由于种类及所在地的不同而存在离子成分差异，但大部分盐水均以 Cl−为主要阴离子，Na+、Ca2+为主要的阳离子，附加少量的 K+、Mg2+等[3]。实验发现盐离子的存在会增加CO2-盐水系统的界面张力，且IFT增量与盐浓度呈线性增加关系[4-5]。此外，不同的阳离子对IFT增量具有不同的影响，如Ca2+的电荷数是Na+的2倍，而CaCl2对IFT增量的增加斜率（3.53 mN·L·m−1·mol−1）约为NaCl（1.43 mN·L·m−1·mol−1）的2.5倍[5]，有实验研究者认为，是由Ca2+与Na+的阳离子价态差异引起的[5]。然而，不同盐成分导致不同CO2-盐水系统IFT增量的内在机理还尚未见报道。此外，由于离子电荷数、兰纳-琼斯势（Lennard-Jones (L-J) potential）参数、原子质量等特性参数随着离子同时变化，导致实验中不能采用控制变量法进行单一原子特性参数变化的研究，所以难以实现离子各特性参数对 CO2-盐水系统界面张力变化影响规律的单独讨论。

除实验研究外，分子动力学模拟作为研究CO2-盐水体系界面张力的有效方法已被国内外学者广泛使用。da Rocha等[6]在 318 K和 20 MPa下采用SPC/E 水分子和 EPM2的 CO2分子模型研究了CO2-纯水界面的 IFT，发现了分子热波动引起的毛细波现象。Li等[7]采用EPM2的CO2模型以及SPC/E和TIP4P的水分子模型，在303～393 K and 2～50 MPa的范围内模拟了CO2-NaCl和CO2-CaCl2系统，发现了离子电荷较离子半径对IFT值的影响更大。Zhao等[8]采用柔性F3C水分子模型以及柔性EPM2 CO2分子模型得到了与实验数据相一致的CO2-纯水以及CO2-CaCl2系统的IFT值，同时分析出原子力对IFT具有一定的影响作用并运用周向分布函数推测出界面处分子的排布规律。然而，目前这些MD研究尚未对盐溶质的原子特性参数与IFT值的关系进行详细研究。

本文应用分子动力学模拟的方法，提出了虚拟系统与真实系统的比照模拟体系，研究了343 K和20 MPa 条 件 下 CO2-NaCl、 CO2-CaCl2和CO2-(NaCl+CaCl2)盐水系统的界面张力等微观性质，分析了不同阳离子种类及成分、阳离子电荷数、兰纳-琼斯势L-J势能参数、原子质量等原子特性参数对IFT的影响，探讨了以上各参数对IFT的单独作用机理。此外，本文还建立了IFT值与离子强度之间的直接联系，为CO2在深部盐水层中的存储提供了理论依据。

1 研究对象及方法

本文的研究对象为343 K和20 MPa条件下，CO2-NaCl、CO2-CaCl2溶液和 CO2-(NaCl+CaCl2)混合盐溶液界面系统。计算中考虑了分子间非键结作用及分子内键结作用。其中分子间的非键结作用包括范德华力和库仑静电力，用 L-J势能函数[9]描述范德华力，库仑定律描述分子间库仑静电力，采用PME技术[10]模拟分子间长程库仑作用力，范德华作用截距设定为0.9 nm[11]。而分子内的键结作用则包括键拉伸和键角弯曲，分别采用谐波势能函数[8]进行模拟。两原子i和j之间的L-J势能函数详见式(1)。

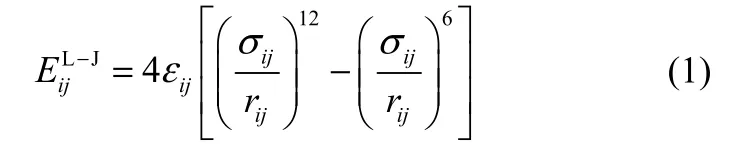
式中，εij=(εiiεjj)1/2，σij=(σiiσjj)1/2，rij为原子i和j之间的距离；ε为L-J势能曲线中的势能阱深度；势能阱越深，两点间引力越大，当势能为零时，两点间的距离等于σ。

计算系统中CO2、水分子及离子的力场参数列于表1。其中，水分子采用了柔性F3C模型[12]，CO2采用柔性 EPM2模型[13]，Na+、K+和 Cl−采用Chandrasekhar等[14]开发的力场，Ca2+采用Aqvist[15]开发的力场。

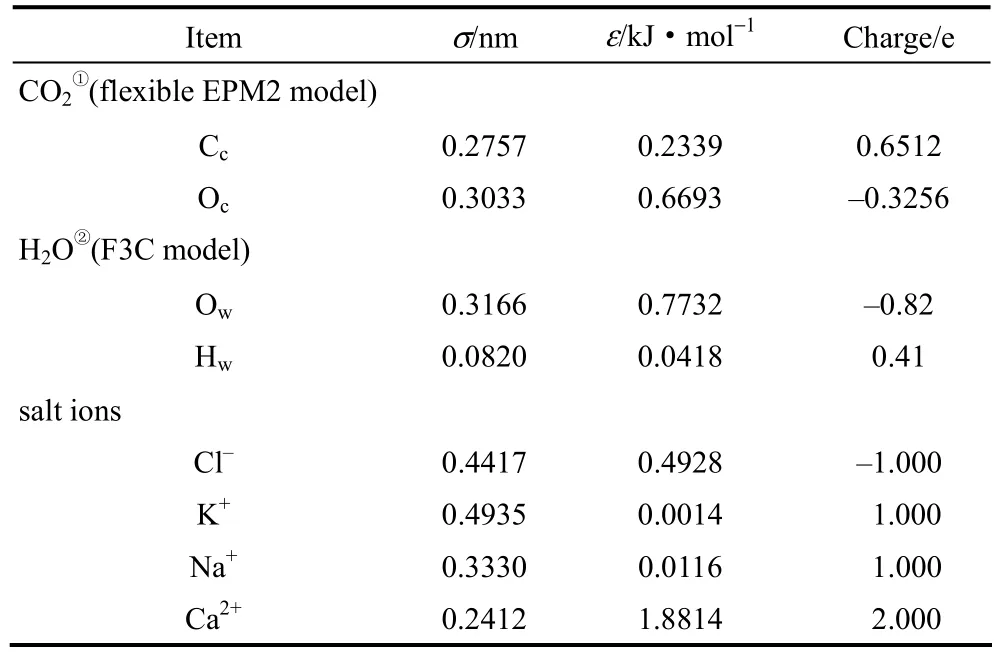
表1 CO2、H2O及盐离子参数Table 1 Parameters of CO2, H2O and salt ions

1.1 虚拟系统

离子的电荷数(q)、L-J势参数(ε、σ)、原子质量(m)等均可表征盐离子原子特性参数。本研究采用控制变量法依次研究上述参数对IFT的单独作用。对给定离子类型的某种盐而言，由于离子电荷和 L-J参数是相互依赖并共同作用于原子特性，从而在实验角度上不可能实现改变单一变量的操作。然而MD模拟则可设置只改变某一参数而确保其他参数不变的盐离子虚拟系统，故而对于实现控制变量的研究思路具有其独特的优势。为此，本文设置了CO2-NaCl和CO2-CaCl2溶液的虚拟系统，列于表2。表2中系统1 （CO2-NaCl）、系统2（CO2- CaCl2）、系统11（CO2-KCl）为真实系统，系统3*～10*（上标为“*”的系统）为虚拟系统，各虚拟系统的变化参数列于相应括号内。由于氯离子在深部盐水层中占据阴离子大部分份额[3]，故本文仅选用Cl−作为阴离子且不探讨阴离子种类及原子参数对 IFT的影响。

表2 真实系统和虚拟系统的计算工况Table 2 Actual and fictitious simulation systems of CO2-electrolyte solution

1.2 系统建模

本文应用分子模拟软件 Gromacs4.5[16]进行计算。计算中涉及的CO2-盐水系统均采用三维周期性边界条件，初始计算域（模拟盒子）的尺寸为4 nm× 4 nm×16 nm。其中，模型中部占z轴长度为8 nm区域内为 4323个水分子和与盐浓度一致的相应个数的盐离子，例如盐浓度为1.8 mol·L−1时的NaCl溶液，建模时设置139个Na+及Cl−。盐水两侧分别为占z轴长度为4 nm的CO2，为使计算更快达到平衡，CO2分子个数根据计算工况温度压强下的CO2实验密度值确定，343 K和20 MPa条件下CO2分子数为 1472。以 CO2-NaCl溶液（盐浓度 1.8 mol·L−1）系统为例，建立的模型示于图1。

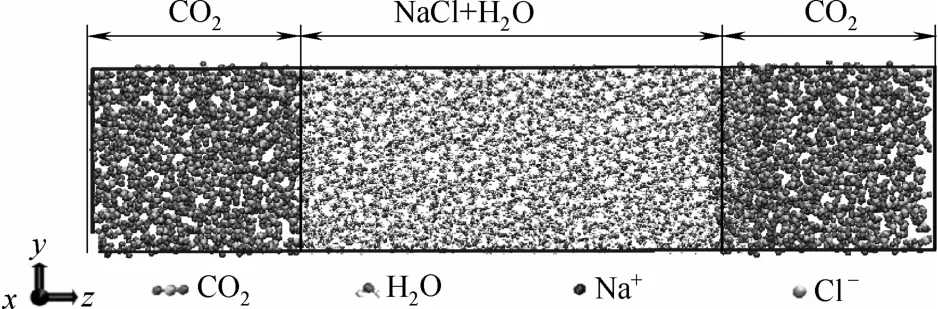
图1 CO2-NaCl溶液系统分子模拟示意图Fig.1 Snapshot of supercritical CO2-NaCl solution

计算采用NPZT系综条件。温度及压强的耦合分别采用基于 Berendsen耦合器的 Velocity Rescaling方法[17]和Semi-isotropic方法[18]。模拟选用Leap-Frog算法[19]以1 fs的时间步长求解运动方程。由于系统20 ns后达到平衡，故取25～30 ns内的模拟结果作为有效数据进行分析，IFT（γ）的定义为界面上正向（z方向）和侧向（x和y方向）压强张量分量的差异[20]。因系统包括两个界面，γ可表示为

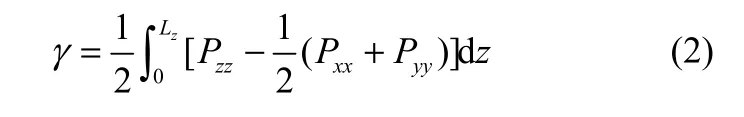
式中，Pxx、Pyy、Pzz分别为沿x、y、z方向压强张量对z向的角分量。

2 结果与讨论

2.1 模型验证

本文分别模拟了343 K和20 MPa条件下，盐浓度为 0.9、1.8、2.7 mol·L−1的 CO2-CaCl2和CO2-NaCl盐水系统，IFT增量（Δγ）的计算结果示于图2。其中，计算Δγ时所选取的基准为CO2-纯水系统，该系统在此温度和压强下的IFT值为31.8 mN·m−1[8]。由图2可以看出，CO2-NaCl与CO2-CaCl2溶液系统的 IFT增量值均与盐浓度呈线性关系；Ca2+的电荷数是Na+的2倍，而CO2-NaCl系统的IFT增量值与盐浓度关系的实验值曲线斜率为CO2-CaCl2系统的2.5倍[5]；CO2-盐水系统的IFT模拟结果与实验数据吻合较好[5]，说明本文的计算模型具有一定的准确性和可靠性。

图2 CO2-NaCl及CO2-CaCl2系统IFT增量与盐浓度的关系Fig.2 Incremental IFTs for CO2-CaCl2and CO2-NaCl solution systems as a function of salinity

2.2 阳离子原子特性参数的影响

盐离子的原子特性参数包括：阳离子电荷数(q)、L-J势参数(ε、σ)、原子质量(m)等。讨论阳离子对IFT增量的影响必然要对以上各因素进行单独分析。本节通过前文介绍的虚拟系统进行模拟，探讨了各因素对IFT增量的影响及规律。

2.2.1 阳离子电荷数(q)的影响 为将阳离子电荷数从诸多影响因素中独立出来，得到仅因电荷数差异而导致的IFT变化规律，本文对表2中的虚拟系统3*（Na2+）与系统4*（Ca+Cl−）进行了模拟。在这些虚拟系统中，只改变了阳离子电荷数而保持其他阳离子特性参数不变。例如，将 NaCl的钠离子由Na+变为Na2+（系统3*），将CaCl2的钙离子由Ca2+变为Ca+（系统4*）。虚拟系统3*、4*的盐浓度均选为1.8 mol·L−1，计算结果示于图3。

图3 虚拟及真实系统IFT增量计算结果Fig.3 Incremental IFTs for fictitious and real systems at salinity of 1.8 mol·L−1

由图3阳离子电荷数比照组可以看出，在盐浓度为1.8 mol·L−1时，模拟所得到的Na+Cl−、Ca2+、Na2+和Ca+Cl−作为溶质系统的Δγ分别为2.3、5.7、5.1和2.9 mN·m−1。由此可见，当盐浓度一致时，在相同阳离子电荷数的情况下（系统1与4*、系统2与3*），Δγ值十分接近；二价阳离子Ca2+（系统2）和Na2+（系统3*）所引起的Δγ值约为一价阳离子Na+（系统1）与Ca+（系统4*）的2倍；由此看出，阳离子电荷数是导致Δγ值变化的主要原因。但是，两个二价系统（Ca2+和Na2+）之间及两个一价系统（Na+和Ca+）之间的Δγ值并不相等，均存在0.6 mN·m−1的差异，由此可预测仍有其他原子特性参数会对Δγ产生影响。

2.2.2 L-J势能参数（ε、σ）的影响 为得到L-J势能参数ε和σ对Δγ值的影响，本文另增加了KCl溶液参照系统（表2中系统11）。Na+Cl−（系统1）、Ca2+（系统2）、K+Cl−（系统11）3个真实系统的L-J参数比较关系为εK+ ＜ εNa+ ＜ εCa2+和σK+ ＞ σNa+＞ σCa2+（表1）。计算所得3个真实系统的IFT增量为：ΔγK+ ＜ ΔγNa+ ＜ ΔγCa2+，与实验数据相一致[5,21-22]。但仅从这些真实系统的数据仍无法分析ε与σ对Δγ值的单独影响。因此，本文继续研究了系统 5*（Na+Cl−(with εCa2+)）、6*（Na+Cl−(with σCa2+)）、8*（Na+Cl−(with εK+)）、9*（Na+Cl−(with σK+)），计算结果示于图3。当保持系统1（Na+Cl−）Na+的电荷数及σ等原子特性参数不变，仅将参数ε改为εCa2+（系统5*）和εK+（系统8*）时，得到ΔγεK+＜ΔγεNa+＜ΔγεCa2+。改用 εK+时，Δγ相对于 εNa+下降了 0.4 mN·m−1，而用 εCa2+时 Δγ则相对 εNa+上升了 1.1 mN·m−1（见图3中L-J势参数ε比照组）。由此可推论，参数ε值越大（L-J势的势井越深），Δγ值越大。依据 Lorentz-Berthelot混合定律可对此推论进行理论分析，在离子与水中的H原子或O原子之间的ε越大，离子与水分子间的范德华力作用就越强，进而含水电解质溶液中分子的结合更加稳固，最终导致了CO2与盐水界面的IFT值越大。

同样，在系统1的基础上，将Na+的参数σ改变为σCa2+（系统6*）和σK+（系统9*），可得结果：ΔγσCa2+＜ ΔγσNa+ ＜ΔγσK+。由图3中L-J势参数σ比照组（系统1、6*和9*）可知，改用σCa2+时Δγ相对于σNa+下降了0.6 mN·m−1，而用σK+时则相对σNa+上升了0.1 mN·m−1。由此可预测，σ越大，Δγ值越大，即增大离子半径将导致IFT增大，但参数σ对Δγ的影响小于ε。总体来说，参数ε与σ对Δγ的影响程度均不及阳离子电荷数对Δγ的主导作用。

2.2.3 原子质量（m）的影响 与讨论 L-J参数方法类似，本文还对虚拟系统7*[Na+Cl−(with mCa2+)]、系统10*[Na+Cl−(with mK+)]与真实系统1（Na+Cl−）（图3原子质量比照组）进行原子质量的影响分析。已知原子质量的大小关系为：mNa+ ＜ mCa2+ ≈mK+。由图 3 的计算结果可以发现：ΔγmNa+ ＜ΔγmCa2+≈ΔγmK+，改用mCa2+（系统7*）和mK+（系统10*）的Δγ相对于mNa+（系统1）均下降了0.2 mN·m−1。由此可见，原子质量越大，Δγ就越大，但原子质量对于Δγ的影响程度相较电荷数及LJ参数而言较小。

2.3 阳离子特性及离子浓度的综合影响

由上述讨论可知，溶液电解质不同时，阳离子的电荷数是导致 CO2-盐水系统 IFT变化的主导因素；而电解质（或是阳离子电荷数）相同时，界面处盐离子的解吸能力会随着盐浓度升高而增强[8]，进而导致 IFT增量随着离子浓度呈现出线性关系（图 2）。然而，目前综合考虑阳离子及离子浓度两大因素对IFT增量进行定量的相关性分析尚未见报道。图2中CO2-CaCl2和 CO2-NaCl系统无论是模拟值亦或是实验值，Δγ随盐浓度变化的曲线斜率比值均约为 2.5，与离子浓度比（1.5:1）或是阳离子电荷数比（2:1）均不一致。为此本文选取离子强度（I）这一物理量，综合考虑离子电荷数及离子浓度因素，对IFT变化进行分析。离子强度的计算公式为

式中，I为离子强度，ci为离子i的摩尔浓度，zi为离子i的电荷数。离子强度对IFT的影响研究可能揭示溶液电性强弱对界面结构的影响。

本文计算得到的CO2-NaCl和CO2-CaCl2溶液系统的Δγ值与离子强度的关系示于图4(a)。由图中可看到，这两个系统的 Δγ与离子强度的关系曲线的斜率十分接近，其中CO2-CaCl2溶液系统的斜率略微小于CO2-NaCl系统的斜率。

为进一步验证所观测到的Δγ和I之间的关系，本文模拟分析了CO2-混合盐系统，分别设置了总盐浓度为0.9、1.8和2.7 mol·L−1的NaCl和CaCl2混合盐溶液，并同时改变各溶液中 NaCl的摩尔分数为 20%、40%、60%和 80%依次进行模拟。不同NaCl/CaCl2（摩尔比）时IFT随浓度的变化规律示于图4(b)。由该图可知，Δγ和混合盐的总浓度呈线性关系，且混合盐系统的 Δγ和盐浓度的斜率介于纯NaCl和纯CaCl2系统之间。

本文通过分析IFT斜率与两种盐摩尔比之间的关系，发现混合盐引起的IFT斜率δmix可用插值法进行计算

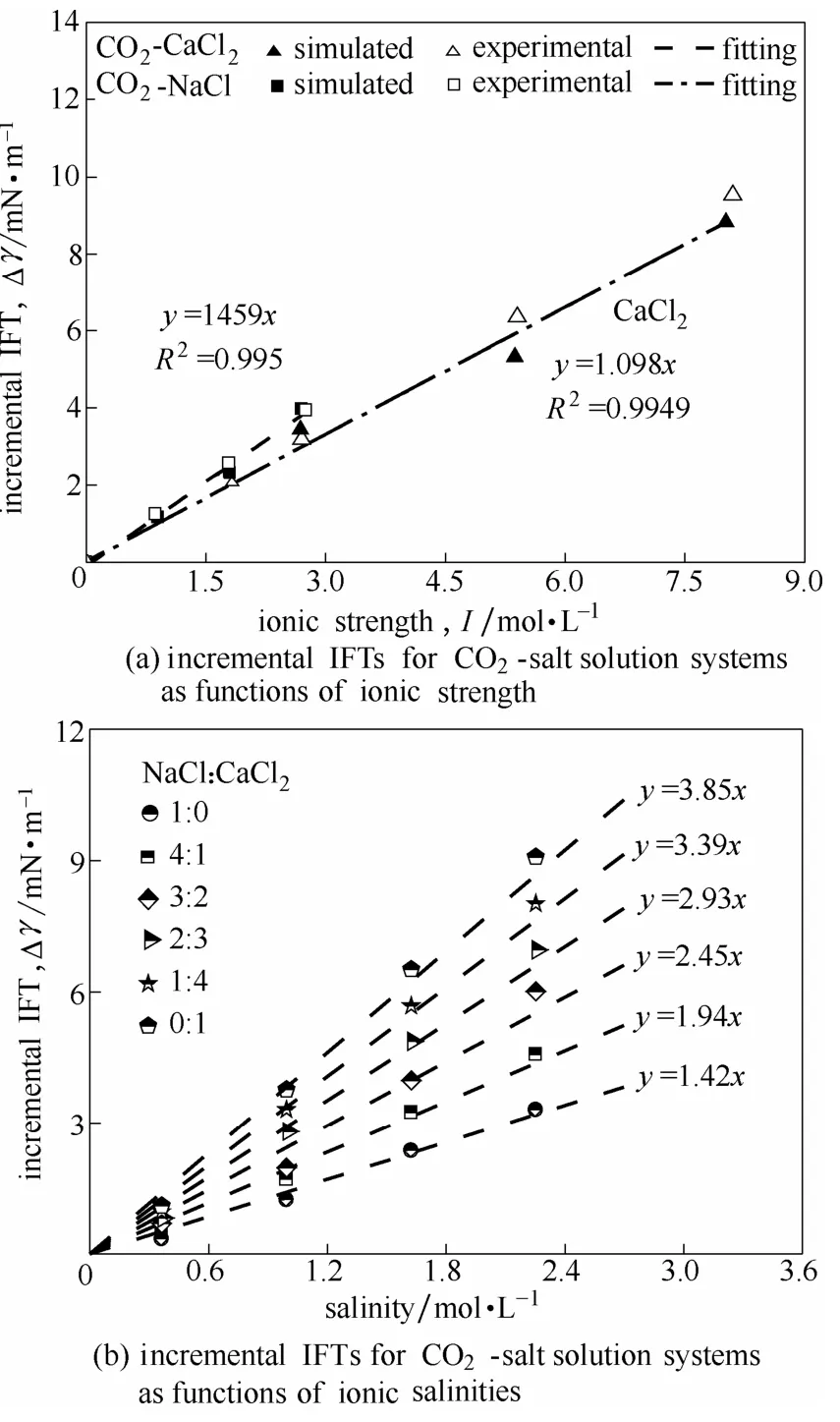
图4 CO2-盐水系统IFT增量与离子强度、盐浓度的关系Fig.4 Incremental IFTs for CO2-salt solution systems as functions of ionic strength and salinities

式中，xi为盐类i占混合盐的比例，δi为纯盐i引起的IFT增加斜率。式（4）可以为预测混合盐的IFT提供依据。

计算所得Δγ随着NaCl组分变化的关系示于图5(a)。由图可知，Δγ与 NaCl组分的关系曲线斜率随着混合盐总浓度的上升而下降；在 NaCl组分固定时，Δγ随着混合盐总浓度呈现出与实验数据[5]一致的线性变化。

本文对图5(a)的数据进一步处理，纵坐标改变为单位离子强度下的Δγ，结果示于图5(b)。由图中可以看出，在不同混合盐总浓度情况下，单位离子强度的Δγ随NaCl摩尔组分几乎不变。由此可知，在强电解质溶液中，将离子产生的电场影响进行量化并取单位值之后，Δγ则与溶液中盐的成分（NaCl/CaCl2）无明显关联，该现象为混合盐系统IFT的预测提供了重要依据。

根据以上研究，本文进一步预测：CO2-盐水系统的单位离子强度的 Δγ的大小可能与盐溶液电解质的类型关系不大，在某一确定环境条件下，Δγ/I极可能对于通用型矿物电解质(例如本文所考虑的Na+、Ca2+、K+和 Cl−所构成的盐)为一定值，可为工程上预测不同盐溶液的类型、组分及浓度下的IFT值提供指导。

3 结 论

本文采用分子动力学模拟的方法对343 K和20 MPa条件下不同盐浓度的CO2-NaCl、CO2-CaCl2和CO2-(NaCl+CaCl2)混合溶液系统进行了盐离子对IFT增量的影响研究，得到以下结论。

（1）IFT增量的变化主要来自于阳离子电荷数，而L-J势能力场参数ε、σ及原子质量m也对IFT增量产生影响，但相对于电荷数影响较小。

（2）CO2-NaCl和CO2-CaCl2界面的IFT增量随离子强度成线性变化且斜率相近，溶液中离子强度对IFT的影响是具备量化条件的。

（3）不同浓度及混合盐摩尔比下单位离子强度IFT基本趋于定值，即CO2-盐水系统中Δγ直接与I相关，而与盐溶液电解质的类型和组分无关，可为工程上预测IFT值提供指导。

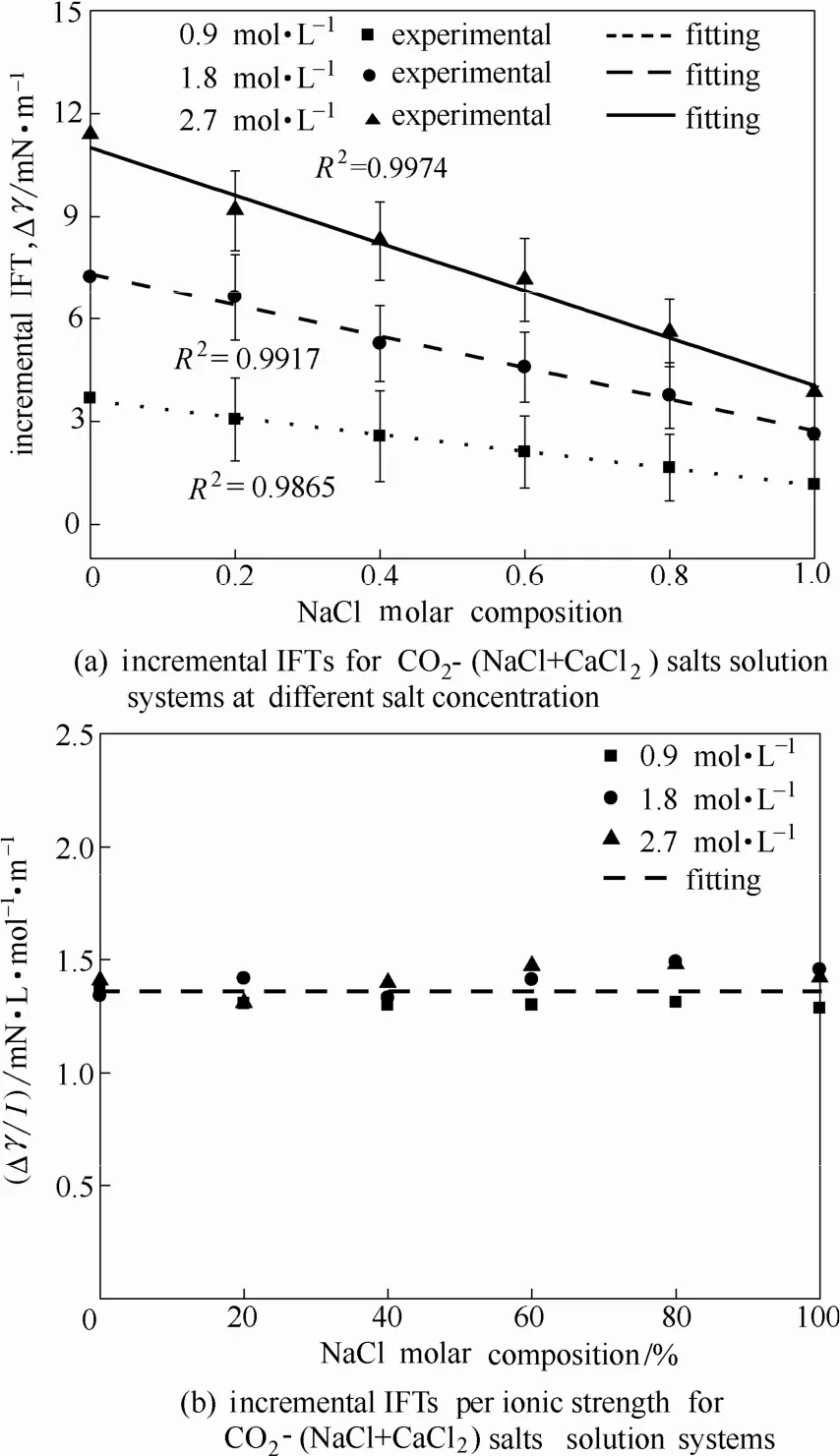
图5 CO2-混合盐系统IFT增量及单位离子强度IFT增量Fig.5 Incremental IFTs and incremental IFTs per ionic strength for CO2- mixed salts solution systems as functions of NaCl molar compositions

符 号 说 明

I ——离子强度，mol·L−1

m ——原子质量

Pxx——x方向压强张量对z向的角分量

Pyy——y方向压强张量对z向的角分量

Pzz——z方向压强张量对z向的角分量

q ——离子的电荷数，e

rij——原子i和j之间的距离，nm

xi——盐类i占混合盐的比例

γ——界面张力，mN·m−1

Δγ——界面张力增量，mN·m−1

δi——纯盐i引起的IFT增加斜率混合盐引起的IFT斜率

ε——L-J势能曲线中的势能阱深度，nm

σ——势能为零时，两点间的距离，nm

[1] ECCLES J K, PRATSON L, NEWELL, R G, et al. Physical and economic potential of geological CO2storage in saline aquifers[J]. Environ. Sci. Technol., 2009, 43(6): 1962-1969.

[2] SZULCZEWSKI M L, MACMINN C W, HERZOG H J, et al. Lifetime of carbon capture and storage as a climate-change mitigation technology[J]. Proc. Natl. Acad. Sci., 2012, 109(14): 5185-5189.

[3]BACHU S, BENNION D B. Interfacial tension between CO2, freshwater, and brine in the range of pressure from (2 to 27) MPa, temperature from (20 to 125)℃, and water salinity from (0 to 334000) mg·L−1[J]. J. Chem. Eng. Data, 2009, 54(3): 765-775.

[4] CHALBAUD C, ROBIN M, LOMBARD J M, et al. Interfacial tension measurements and wettability evaluation for geological CO2storage[J]. Adv.Water Resour., 2009, 32(1): 98-109.

[5]AGGELOPOULOS C A, ROBIN M, PERFETTI E, et al. CO2/CaCl2solution interfacial tensions under CO2geological storage conditions: influence of cation valence on interfacial tension[J]. Adv. Water Resour., 2010, 33(6): 691-697.

[6] DA ROCHA S R P, JOHNSTON K P, WESTACOTT R E, et al. Molecular structure of the water-supercritical CO2interface[J]. J. Phys. Chem. B, 2001, 105(48): 12092-12104.

[7] LI X S, ROSS D A, TRUSLER J P, et al. Molecular dynamics simulations of CO2and brine interfacial tension at high temperatures and pressures[J]. J. Chem. Eng. Data, 2013, 117(18), 5647-5652.

[8] ZHAO L L, LIN S C, MENDENHALL J D, et al. Molecular dynamics investigation of the various atomic force contributions to the interfacial tension at the supercritical CO2-water interface[J]. J. Phys. Chem. B, 2011, 115(19): 6076-6087.

[9] 范康年. 物理化学[M]. 2版. 北京:高等教育出版社，2005:222. FAN K N. Physical Chemistry [M]. 2nd ed. Beijing: Higher Education Press, 2005: 222.

[10]DARDEN T, YORK D, PEDERSEN L. Particle Mesh Ewald: an N·log (N) method for Ewald Sums in large systems[J]. J. Chem. Phys., 1993, 98(12): 10089-10092.

[11]DE-LARA L S, MICHELON M F, MIRANDA C R. Molecular dynamics studies of fluid/oil interfaces for improved oil recovery processes[J]. J. Phys. Chem. B, 2012, 116(50): 14667-146676.

[12]LEVITT M, HIRSHBERG M, SHARON R, et al. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution[J]. J. Phys. Chem. B, 1997, 101(25): 5051-5061.

[13]NIETO-DRAGHI C, DE BRUIN T, PEREZ-PELLITERO J, et al. Thermodynamic and transport properties of carbon dioxide from molecular simulation[J]. J. Chem. Phys., 2007, 126(6): 064509.

[14]CHANDRASEKHAR J, SPELLMEYER D C, JORGENSEN W L.Energy component analysis for dilute aqueous solutions of lithium (1+), sodium (1+), fluoride (1−), and chloride (1−) ions[J]. J. Am. Chem. Soc., 1984, 106(4): 903-910.

[15]AQVIST J. Ion-water interaction potentials derived from free energy perturbation simulations[J]. J. Chem. Phys., 1990, 94(21): 8021-8024.

[16]PRONK S, PALL S, SCHULZ R, et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit[J]. Bioinformatics, 2013, 29(7): 845-854.

[17]BUSSI G, DONADIO D, PARRINELLO M. Canonical sampling through velocity rescaling[J]. J. Chem. Phys., 2007, 126(1): 014101.

[18]BERENDSEN H J, POSTMA J P M, VAN GUNSTEREN W F, et al. Molecular dynamics with coupling to an external bath[J]. J. Chem. Phys., 1984, 81(8): 3684-3690.

[19]HOCKNEY R, GOEL S, EASTWOOD J. Quiet high-resolution computer models of a plasma[J]. J. Comput. Phys., 1974, 14(2): 148-158.

[20]ALEJANDRE J, TILDESLEY D J, CHAPELA G A. Molecular dynamics simulation of the orthobaric densities and surface tension of water[J]. J. Chem. Phys., 1995, 102(11): 4574-4583.

[21]LI X S, BOEK E S, MAITLAND G C, et al. Interfacial tension of (brines + CO2): CaCl2(aq), MgCl2(aq), and Na2SO4(aq) at temperatures between (343 and 423) K, pressures between (2 and 50) MPa, and molalities of (0.5 to 5) mol·kg−1[J]. J. Chem. Eng. Data, 2012, 57(5): 1369-1375.

[22]PEGRAM L M, RECORD M T J. Hofmeister salt effects on surface tension arise from partitioning of anions and cations between bulk water and the air-water interface[J]. J. Phys. Chem. B, 2007, 111(9): 5411-5417.

Ion effect on interfacial properties of CO2-brine system

JI Jiayuan, ZHAO Lingling, LI Siyu
(Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, School of Energy & Environment, Southeast University, Nanjing 210096, Jiangsu, China)

Interfacial tension of CO2-NaCl, CO2-CaCl2and CO2-(NaCl+CaCl2) solution systems was studied at different salt concentration and ratio by molecular dynamics simulation, in order to understand influence of different salt ions at molecular level. The results showed that the presence of salt ions increased interfacial tension between CO2and water, which majority was caused by number of cationic charges and the rest was by cation atomic properties such as Lennard Jones potential parameters and atomic mass. The interfacial tension increment of these three systems were all linearly dependent on ionic strength, but the slope had no relationship to types of salt solutions. This founding would provide theoretical guidance for IFT prediction.

CO2-brine system; interfacial tension; molecular simulation; atomic characteristic parameter; ionic strength

Prof. ZHAO Lingling, zhao_lingling@seu.edu.cn

TQ 021.2

：A

：0438—1157（2017）01—0223—07

10.11949/j.issn.0438-1157.20160771

2016-06-02收到初稿，2016-09-30收到修改稿。

联系人：赵伶玲。

：季佳圆（1993—），女，硕士研究生。

国家自然科学基金项目（51106027）。

Received date: 2016-06-02.

Foundation item: supported by the National Natural Science Foundation of China (51106027).