基于区域中心点的多层次数据集密度聚类算法
魏姁妲, 逄焕利
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
基于区域中心点的多层次数据集密度聚类算法
魏姁妲, 逄焕利*
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
通过k-dist图和DK分析方法对非均匀数据进行密度分区并选择半径,确定各密度区域的初始区域中心点,然后调用改进后的快速聚类算法进行聚类。在两种数据集上进行了算法实验验证,有效地聚类多层次数据集,提高了效率和准确率。
非均匀密度聚类; DBSCAN; 区域中心点; K邻域; DK分析
0 引 言
基于密度的聚类算法因其事先不需要设定聚类的个数,同时能发现各种形状的簇等优点为人关注,其代表算法有DBSCAN、OPTICS、DENCLUE等。但在解决实际问题中大量存在的密度非均匀数据时,效果常不能令人满意。目前,研究人员基于这种缺陷也提出了相应的改进算法:文献[1] 提出了依据数据分区思想的PDBSCAN算法,通过分析多层次密度点的分布特性将其标记为多个局部区域,再分别对各区域做合并操作;文献[2]提出PACA-DBSCAN算法,该算法采用k-means算法(或蚁群聚类算法)对数据集进行分区,并用k-dist图确定分区密度参数,实现局部聚类;文献[3]则采用DBSCAN算法对每个数据集对象的k-dist值进行聚类,通过获取不同的Eps参数,再用传统DBSCAN算法进行聚类。
文中提出处理非均匀密度数据的改进算法。通过k-dist图和DK分析方法,发现各密度分区及其对应的初始中心点和半径,最后分别对各区域进行聚类。同时,文中提出一种快速聚类算法来提高各密度区域聚类时的效率。实验表明,本算法可以有效地聚类非均匀密度数据,时间效率及准确率较传统算法有所提升。
1 DBSCAN算法
1.1 DBSCAN算法
DBSCAN算法是基于密度的典型算法,其主要思想为:寻找所有核心对象的Eps邻域内直接密度可达的密度相连对象,将这些对象合并成一类。它具有聚类速度快、能够处理噪声点并发现各种形状的簇等优点,该算法通过过滤低密度区域来发现密度较大的样本点。算法涉及的基本定义如下。
1.1.1 Eps邻域
给定对象半径Eps内的区域。
1.1.2 核心对象
在数据集D中,如果对象p的Eps邻域内包含的对象不少于指定参数MinPts,则称p为核心对象。
1.1.3 直接密度可达
在数据集D中,存在一点q在点p的邻域内,且p是核心对象,则称点q是从p出发的直接密度可达[4]。
1.1.4 密度可达
存在点链p1,p2,…,pn,其中p1=q,pn=p,使pi+1是从pi直接密度可达,则称点p是从点q关于参数Eps,MinPts密度可达的[4]。
1.1.5 密度相连
存在点o,使得点p和q都从点o密度可达,则称点p和q是在给定Eps,Minpts参数下密度相连的。
1.2 DBSCAN算法可改进性
传统的DBSCAN算法在聚类前,会对Eps与MinPts设置全局统一的值,依据这两个参数寻找密度相连的点的最大集合,完成最终聚类。但这种参数设定方式忽略了密度不均匀分布的数据集时的聚类:当全局变量Eps值适用于密度分布稠密的区域聚类时,对于密度分布稀疏的区域易产生大量的孤立点;而当对密度稀疏的区域适用时,对密度稠密的区域会产生大量的噪声点被聚到相应的簇中。因此可见,这种选择全局变量的做法并不适用于密度分布不均匀的数据集,会使算法在处理多层次数据集聚类时准确度降低。
另外,传统的算法在对象邻域查询时存在一定的冗余操作:需要对每个样本点都进行邻域查询,来判断Eps邻域内的点是否大于MinPts,从而判断是否为核心点,再根据核心点寻找其密度相连的点,将其聚为一类。然而在多个对象邻域出现交集时,部分对象就会被重复扫描,如此操作很大程度上降低了算法的时间效率。
2 改进的DBSCAN算法
2.1 相关概念
2.1.1 密度层次
具有密度分布情况相近的点的集合称为同一密度层次。本算法从小到大排列各对象的第k个最近邻距离值,根据k-dist图判断数据集的密度层次分类。两种数据集的k-dist示例如图1所示。

图1 k-dist示例图
对比看出,B数据集的密度分布不均匀,分为3个密度层次。
2.1.2 密度水平线
在k-dist图中,变化较为平缓的曲线称为密度水平曲线,落在密度水平曲线上的点密度往往比较相近[5]。图1中,a、b、c即为密度不同的三段密度水平线。
2.1.3 密度转折线
在k-dist图中,变化较为陡峭的曲线称为密度转折线,多用于分隔两个密度不同的对象集[6]。图1中,d、e即为密度转折曲线。
2.1.4 DK分析图
在k-dist图中,取k-dist图中相邻两点的差值,将其绘制成的图形即为DK分析图,并将k-dist图中相邻两点的差值记为DK值。DK分析图中的横坐标为数据点序号,纵坐标为DK差值。
2.1.5 DK邻域
为了排除密度转折线上的点及噪声点而设定的DK值范围。主要计算方法为:令DK值升序排列,取一定比例的DK值计算平均值,表示为Ave(x%);为选择密度水平线上的点,将给定一个阈值δ,DK值邻域即为[Ave(x%)-δ,Ave(x%)+δ],并称Ave(x%)-δ为DK下邻域值,Ave(x%)+δ为DK上邻域值。
2.1.6 区域密度半径
各密度层次下的聚类半径。文中取DK上邻域值对应的最近的DK邻域中的点的k-dist值作为其所在密度分区的半径。
2.1.7 初始区域中心点
各密度层次用于初次聚类的候选核心点[7]。文中将密度水平曲线上的k-dist最小值作为其所在分区的初始区域中心,各分区的其他对象按照k-dist值升序排列存入队列。
2.1.8 核心点(Core point)
某点的密度半径邻域内包含的对象不小于给定参数,我们称这样的点为核心点。文中首先对初始区域中心点进行判断,如不满足条件则选择本密度区域队列中下一对象进行判断,直到满足条件结束。
2.1.9 密度相连
在数据集D中,存在一点q,如果点q既属于类A1,又属于类A2,并且点q的区域半径邻域内的对象数不小于给定参数,那么A1和A2中的核心对象和q是密度相连的[8]。
本算法中对于密度直接可达、密度可达等定义与传统的基于密度算法中的定义相同。
2.2 算法描述
本算法主要思想是:将非均匀密度数据集通过k-dist图分成若干个密度均匀的数据层,在密度均匀的数据层中分别进行聚类,算法的具体步骤如下:
输入:数据集D,K值,DK分析中的x%和δ值,MinPts。
输出:聚类结果集。
1) 密度层次划分。计算数据集D所有对象的k-dist(pi),其中i=1,2,…,n,绘制k-dist分区图,得到各个分区数据集Di。
2)确定密度半径和初始区域中心点:根据DKm=k-distm-k-distm-1(m>1)计算DK值,取前x%比例的DKm计算其平均值Avg(x%),绘制DK分析图。根据2.1.6和2.1.7来确定密度分区的密度半径Epsi及初始区域中心点Oi。
3)确定密度核心点:判断Oi的Epsi内点数是否不小于MinPts,如果条件成立,则确定Oi为本区域的核心点,并将其标记为Ci;否则,选择队列中的下一点进行同样判断。
4)根据确定的核心点Oi,密度区域半径Epsi,调用改进后的快速聚类算法,对各密度区域中的点进行聚类。
5)重复执行步骤3)和步骤4),当所有点都被聚类后停止。
2.3 快速聚类算法
DBSCAN算法将簇定义为密度相连的点的最大集合,它需要检索每一个点及其邻域来寻找密度相连的簇。然而在多个对象的邻域出现交集时,部分对象就会被重复扫描,对每个点都进行邻域查询显然是不值得的[8]。文中快速聚类方法的主要思想为:
1)以Oi为起始点,计算邻域Epsi内的对象数,如果|Neighbors|≥Minpts,则将Neighbors内的所有点均标记为与Oi同类,否则标记为噪音。
2)寻找密度队列Di中未标记类别的下一个核心对象,并按照1)中的方法对邻域内各点进行类别标注。
3)当出现某一个点qi既属于Oi的类又属于Oj的类的情况时,则检查该点与两个类中的核心点是否是密度相连,如果是则将两个类进行合并;如果不是,则规定点qi属于最初被划分到的类中。
4)在所有的密度队列中执行上述方法,直到所有的点都被标记为相应的类结束。
具体步骤如下:
输入:核心点Oi,密度区域半径Epsi,MinPts。
输出:聚成的各个簇Ci
算法伪代码:
while(Di.clustered){
// 以Oi为起始点,扫描邻域Epsi内的对象
Neighbors=NeigborScan(Oi,Epsi);
//满足条件将Neighbors内的所有点均标记为与Oi同类,否则标记为噪音。
if(|Neighbors|>=Minpts){
if(qi.cluster=Oi.cluster){
if(qi.cluster= Oj.cluster){
//某点同属两类判断两类是否满足合并条件
Neigborsi=NeigborScan(qi,Epsi);
if(|Neigborsi|>=Minpts)
Oi.cluster=merge(Oi.cluster,Oj.cluster);
else qi.cluster=Oi.cluster;
}
qi.cluster=Oi.cluster;
}
Neighbors.cluster=Oi.cluster;
}
else Oi.cluster=noise;
Oi= Di.nextUnclusteredCore;
}
3 实验分析
实验采用C语言进行编程,分别使用了一般数据集和UCI数组库的Iris数据集对算法的有效性进行了验证。
3.1 一般数据集
利用人工方法构造了数据集D,包涵30个数据,并按照改进算法的步骤对数据进行聚类:实验首先指定参数k=2,来计算距离各个数据点的距离第二大的值,并升序排列所有k-dist值。通过绘制的2-dist图将数据集D分为三个密度区域,如图2所示。
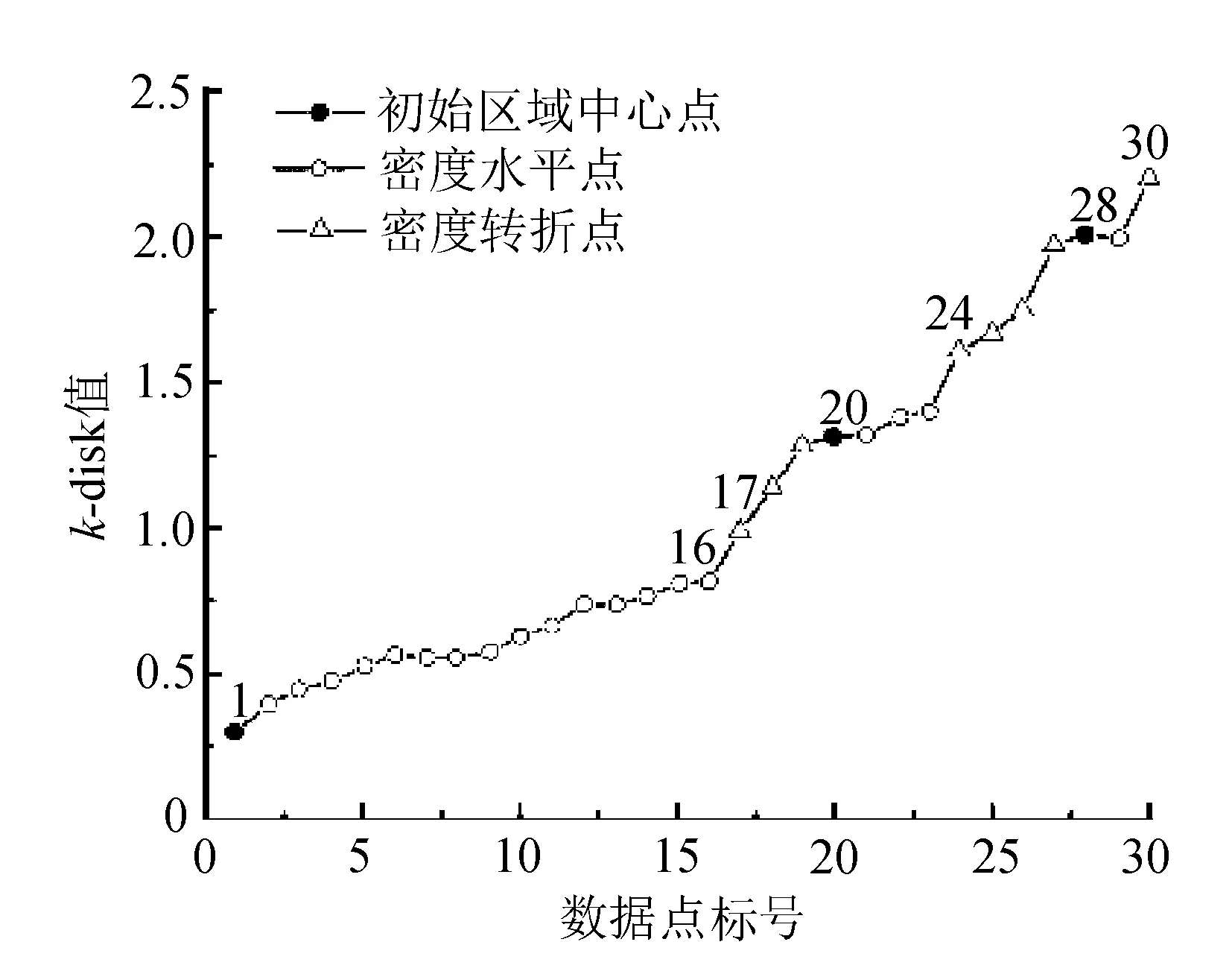
图2 数据集D的2-dist图
通过计算相邻点的k-dist差值得到该数据集的DK分析图。这里对DK值进行升序排列,并取x=80,即取前80%的DK值来做平均计算。经过计算可得Avg(80%)=0.05。为去除密度转折点及噪声点,令δ=0.12,因此可以得到DK邻域为[-0.07,0.17]。又因为k-dist图是从小到大排列的,所以计算出的相邻两点的DK值是非负的,继而得到真实的DK邻域为[0,0.17]。
认为位于DK邻域外的点是密度转折线上的点,如图3所示。
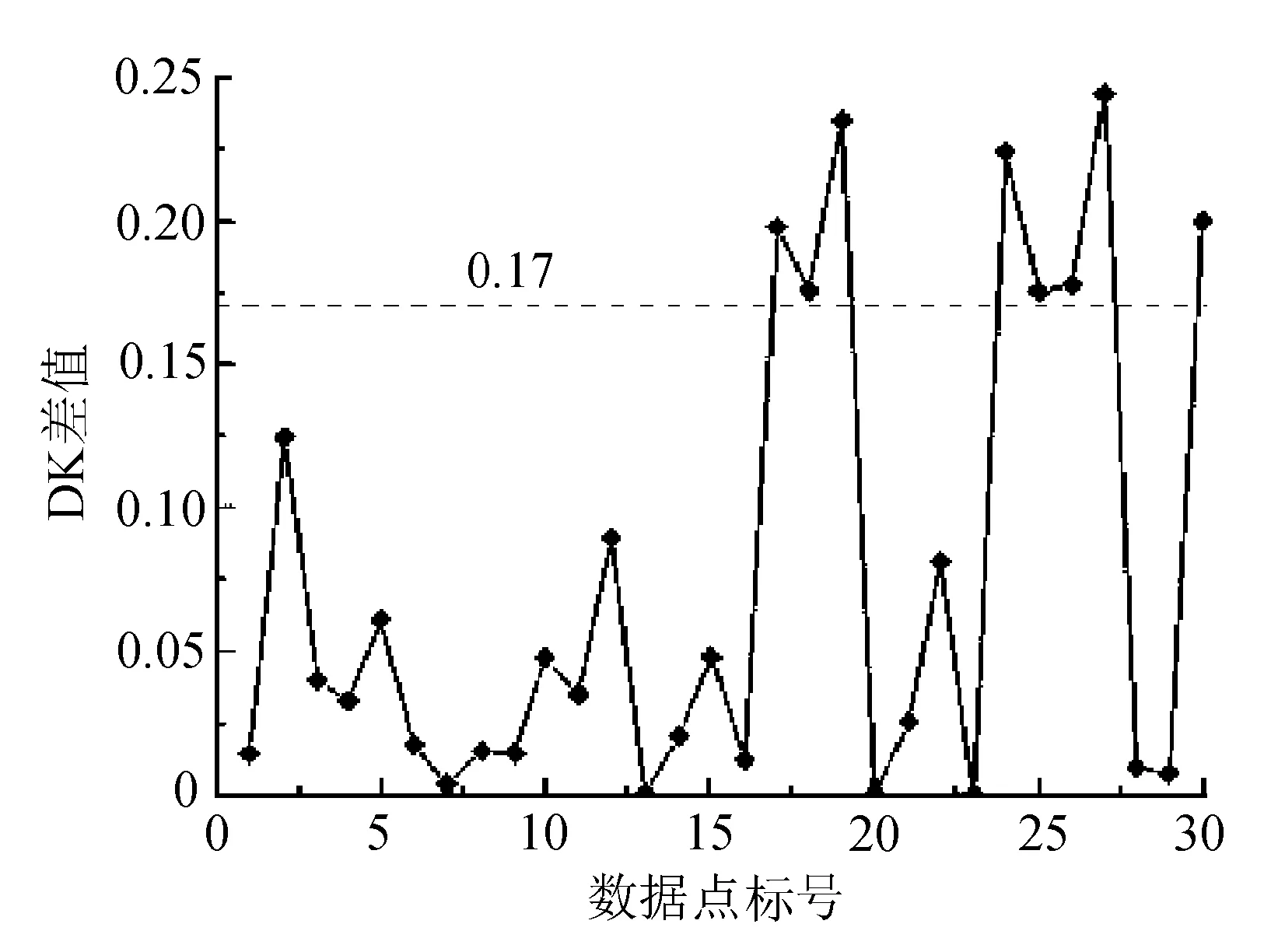
图3 数据集D的DK分析
图中17~19点、24~27点处在DK邻域外,所以认为这些点落在密度转折线上。位于DK邻域内部的点可认为他是在密度水平线上的点,根据2.1.7可以确定该数据集的各个初始区域中心点分别为:点1,点20,点28。根据2.1.6,我们看出该数据集的DK上邻域值为0.17,所以各个区域的密度半径分别为:点16的k-dist值0.81,点23的k-dist值1.35;点29的k-dist值1.96。文中取MinPts=3,对于一般密度不均匀的数据集聚类情况如图4所示。
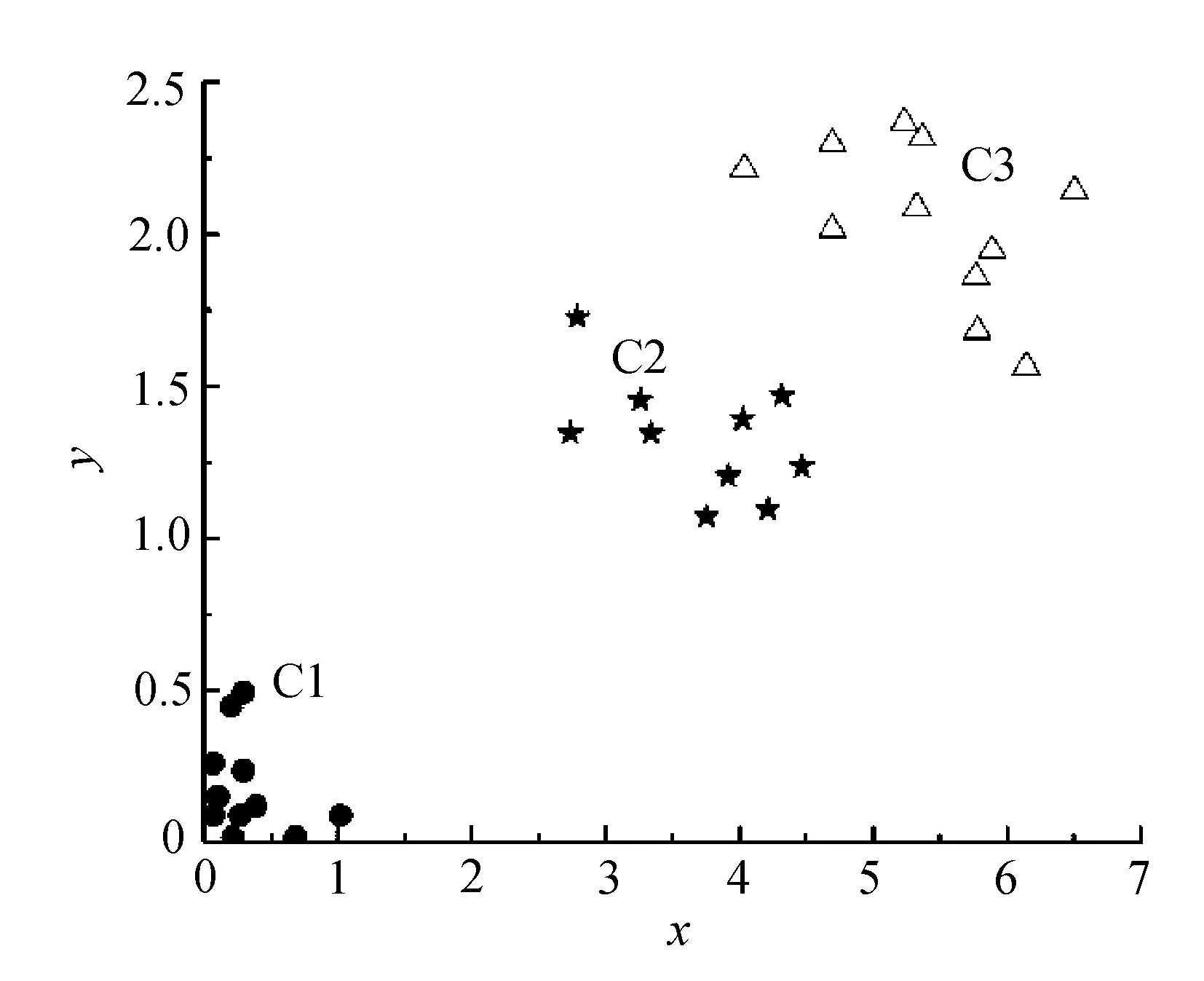
图4 实验结果
3.2 Iris数据集
Iris数据集来自UCI数据库,主要包含了150个关于3种鸢尾花的生物统计数据[9],每种花具有四个属性。为将数据映射在二维坐标上,在实验之前,先对数据进行预处理,取萼片的长宽比(Sepallength/Sepalwidth)作为横轴,花瓣的长宽比作为纵轴(Petallength/Petalwidth)。通过多次试验取平均值,与传统的DBSCAN算法在执行时间、准确率上的对比,其中准确率的计算方法如下:
(1)
具体实验结果见表1。

表1 实验对比结果
传统DBSCAN算法与文中算法的聚类结果分别如图5和图6所示,其中“×”表示噪声点。
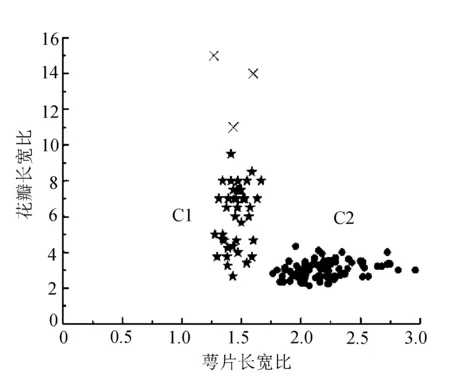
图5 DBSCAN实验结果

图6 文中算法实验结果
4 结 语
由于传统密度聚类法在聚类前期会设定全局参数,使其对密度分布不均匀数据样本聚类效果不佳,基于此提出一种基于区域中心点的密度聚类算法。该算法借助k-dist图确定密度分类,通过DK分析确定区域中心点和区域半径,并通过改进的快速聚类算法分别在两种数据集上进行了验证。通过实验证实,改进后的算法能够对密度分布不均匀数据集进行更好地聚类,算法效率及准确率较传统DBSCAN算法有所提高。
[1] 周水庚,周傲英,曹晶.基于数据分区的DBSCAN算法[J].计算机研究与发展,2000,37(10):1153-1159.
[2] Hua Jiang, Jing Li, Shenghe Yi, et al. A new hybrid method based on partitioning-based DBSCAN and ant clustering[J]. Expert Systems with Applications,2011,38(8):9373-9381.
[3] 熊忠阳,吴林敏,张玉芳.针对非均匀数据集的DBSCAN 过滤式改进算法[J].计算机应用研究,2009,26(10):3721-3723.
[4] 范明,孟小峰.数据挖掘:概念与技术[M].3版.北京:机械工业出版社,2012.
[5] 周董,刘鹏.VDBSCAN:变密度聚类算法[J].计算机工程与应用,2009,45(11):137-153.
[6] 郑丹,王潜平.K-means初始聚类中心的选择算法[J].计算机应用,2012,32(8):2186-2188,2192.
[7] 范敏,李泽明,石欣.一种基于区域中心点的聚类算法[J].计算机工程与科学,2014,36(9):1611-1616.
[8] 李杰,贾瑞玉,张璐璐.一个改进的基于DBSCAN的空间聚类算法研究[J].计算机技术与发展,2007,17(1):114-116.
[9] Iris Data Set(UCI)[DB/OL]. (2012-09-10)[2016-03-20]. http://www.datatang.com/data/551.
Multi-level data set density clustering algorithm based on local center object
WEI Xuda, PANG Huanli*
(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012, China)
Withk-dist plot and DK Analysis, the non-uniform data is classfied and selected for local radius based on different densities to determine the initial local core object. The improved fast clustering algorithm is used for clustering and verified to be efficient in multi-level data set clustering in two data sets experiment.
nonuniform density clustering; DBSCAN; local core object; k-nearest neighbors; DK analysis.
2016-03-20
吉林省科技厅自然科学基金资助项目(201215116)
魏姁妲(1991-),女,汉族,黑龙江绥化人,长春工业大学硕士研究生,主要从事人工智能方向研究,E-mail:332507132@qq.com. *通讯作者:逄焕利(1970-),男,汉族,吉林白山人,长春工业大学副教授,硕士,主要从事数据挖掘和人工智能方向研究,E-mail:panghuanli@ccut.edu.cn.
10.15923/j.cnki.cn22-1382/t.2016.6.12
TP 301.6
A
1674-1374(2016)06-0576-05

