考虑投资和时间成本的地下物流配送路径优化

舒鑫挺

（浙江财经大学，浙江 杭州 310018）

考虑投资和时间成本的地下物流配送路径优化

舒鑫挺

（浙江财经大学，浙江 杭州 310018）

分析了地下物流系统相对于地上物流系统的特殊性，同时考虑投资成本和时间成本，以总成本最低为目标，设计了地下物流配送路径优化模型，然后选用0-1编码的遗传算法进行求解。通过一则算例，根据模型和算法求得了最优路径，表明了设计模型和算法的有效性。

投资成本；时间成本；地下物流配送；路径优化

1 引言

地下物流系统（Underground Logistics System，ULS）也称为称地下货运系统（Underground Freight Transport System，UFTS），是一种相对于传统陆路、水路、航空物流系统而言的新型物流供应系统。目前，全球已有一些发达国家如美国、日本、英国等着手地下物流系统模式的研究与建设。通过经验和实践也表明了地下物流系统既具有快速、精确等效率优势，又可以带来缓解城市交通紧张、美化城市环境、提高城市通达性等社会功能，因此地下物流系统具有非常强大的优越性和非常可观的应用前景。随着我国城市化的不断推进，交通拥堵现象不断加剧，而经济发展带来的物流需求也不断提高，因此地下物流未来或将成为我国新型城市化建设的一大必然选择。

2 地下物流配送的有关问题分析

在设计地下物流配送路径时，地上物流配送路径优化的有关方法还是可以得到应用。但是，必须要考虑到它相对于地上物流配送而存在的特殊之处。

第一，地下物流配送的绝大部分任务都是在地下完成的，其中配送线路设计是最主要的一项任务。地下物流配送与传统的地上公路物流网络化明显不同，目前地下物流配送系统尚未成熟，在配送路径选择时必须通过专门的规划、设计与建设。

第二，地下物流配送系统建设产生比传统地上物流配送系统建设更为庞大的投资，这是目前地下物流配送系统建设中面临的重大问题之一。因此，若是仅仅拿地下物流配送产生的直接经济效益以及直接经济成本来评价这一配送系统，它并不比地上物流配送有优势。所以说，在对地下物流配送路径进行优化设计时，不能盲目地参考目前已有的大量地上物流配送路径优化设计方案，不能盲目地仅仅考虑物流配送成本问题。

第三，地下物流配送相对地上物流配送的最大优势在于运输自由，一般都可以实现直线运输，因此可以明显缩减物流的时间。一般而言，地上物流配送时常会出现拥堵情况，而地下物流配送则可以有效避免这一点。因此，对地下物流配送的路径进行选择时，一般都不需要考虑由于交通拥堵而造成的时间成本损失。

若要对地下物流配送路径进行优化，必须合理选择影响地下物流配送的因素。而在一个地下物流配送系统中，物流配送线路的建设成本、物流运输成本、物流配送时间、物流配送质量、物流配送服务水平等都是对地下物流配送路径选择影响的重要方面。这里，衡量物流配送质量、物流配送服务水平的指标虽然也包含了物流基础设施、平台服务质量等要素，但是这些都是次要的，最主要的在于物流配送的准时性。地下物流配送系统存在环境条件的特殊性，因此在物流配送的过程中，货物达到目的地的准点性也相对容易控制。这一方面为地下物流配送活动带来便利性，另一方面也对地下物流配送路线的可行性提出更高要求。

综合以上因素，本文将同时结合投资成本和时间成本，建立地下物流配送总成本最小化的定量模型进行分析。

3 考虑投资和时间成本的地下物流配送路径优化模型构建

3.1 假设条件

一般而言，地下物流配送系统的建设往往需要更高的投资成本，所以地下物流配送系统更加适用于货物流通规模较高且经济发展较快的城市。为了使本文的模型更加具有说服力，首先需要对模型提出以下几个假设条件：

（1）为了便于模型分析，本文假定物流配送的货物不分种类；

（2）在地下物流配送线路中，每一个节点的位置和节点上的物流需求量都是已知的；

（3）在地下物流配送系统中，所有物流车辆的型号、规模、车辆状况都相同，而且所有车辆都属于自动导向型车辆；

（4）在地下物流配送过程中，车辆的行驶都是匀速的；

（5）所有客户都是接受地下物流配送服务的；

（6）地下物流配送中心的货物数量总是可以满足市场的需求量的。

3.2 理论模型设计

给定一个地下物流配送系统网络，当前需要在N条备用的线路中选择一条最为合适的线路，使得可以以最少的投资和时间成本来完成地下物流配送任务。由于之前假定了城市的货物流通规模较高，所以可以再假定地下物流配送中心与节点无差异化，都可以作为一般的节点来对待，假设这个系统共有M个节点。本文单独考虑货物在各个节点的驻留时间间隔，因此无需再考虑货物在地下物流配送中的“换乘时间”。

假设地下物流配送系统中，第k条线路的路径长度为lk，单位路径的建设投资费用为ck，单位路径的运营成本为dk，在物流配送过程中的速度恒定为v；假设货物从节点i开始出发，到达节点j时，中途共经过h个站，其中每一个站点所停留的时间为tijp，而在起始点i所停留的时间为tij，从节点i到节点j的配送路径全长为Lij；以节点i为始发点，节点j为终点的地下物流配送路线，其货物配送的总量为xij；整个地下物流配送系统的总建设成本为C，总时间成本为T，地下物流配送的总成本为Z；α表示时间成本在总成本中的权重。引入βk和γij两个0-1变量，定义如下：

①若第k条线路被选中，那么βk取值为1，否则，βk取值为0。

②若节点i与节点j之间的路线被选中，那么γij取值为1，否则，γij取值为0。

根据以上变量及假设，关于投资成本和时间成本的模型可表示如下：

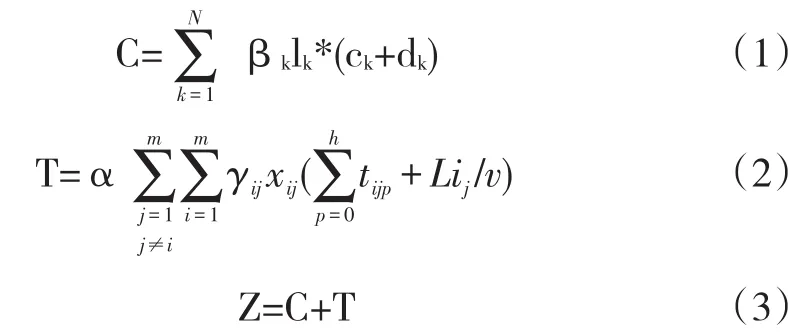
于是，要使得地下物流配送路径优化，就要确保总成本达到最小，即满足如下关系式：

模型的约束条件为：

在约束条件中，式（6）表示地下物流配送的路线是双向路线，即可以逆转，其中G为物流节点所组成的集合；Lmin、Lmax分别表示地下物流配送路线设置长度的最小值和最大值，该式表明了前面所设物流配送路线的规模是合理的；式（7）则表示任何两个物流节点之间都是可达的，Sij则是任意两个物流节点i和j之间的最短路径。

4 计算方法设计

本文拟采用遗传算法对地下物流配送路径进行优化计算。遗传算法是一种通过模拟自然进化规律对最优解进行搜索的方法，它具有内在的隐并行性，在全局搜索优化路径方面具有一定的优势。遗传算法中有一种概率化的搜索优化路径的方法，它能够自动捕捉和指导优化的空间，能够自适应地优化调整路径搜索的方向，而不必要对搜索方式设定规则。

结合地下物流配送路径优化的特征，本文选用0-1编码的遗传算法，对地下物流配送路径进行优化选择，以达到投资成本和时间成本最优。0-1编码的遗传算法步骤如下：

①0-1编码。首先对N条备选的物流配送路线进行编号，所编号码依次为：1，2，3，…，n。因为有N条备选的路线，因此染色体的长度为n。按照0-1编码的原则，对配送路线的编码为：{1，0，0，…，1，0}，其中，“1”表示配送路线被选中，0则表示配送路线未被选中。

②计算适应度。对于种群中的每一个染色体，求出相应的可行解。根据式（3）求出总成本的目标函数值Z，于是适应度的函数为：

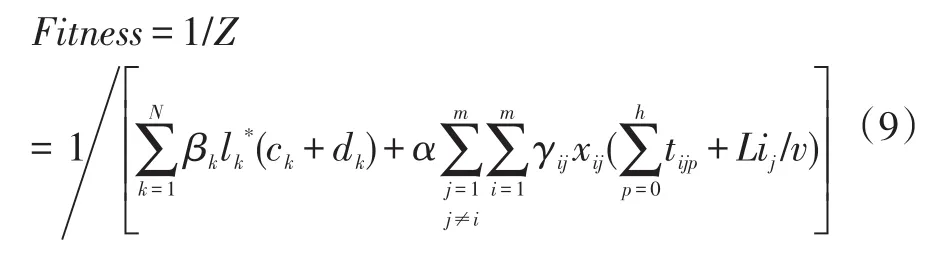
③选择算子。对每一个种群中的P个染色体按照上式的适应度计算结果进行排序，然后将适应度值最大的染色体复制到下一代染色体。再者，对剩余的染色体采用通过基于排名的“轮盘式”选择方式选择要进入下一代种群的算子。

④对算子进行交叉。采用单点交叉的方法对算子进行交叉。比如：

父代I：001|010→子代I：001|100

父代II：010|100→子代II：100|100

⑤算子变异。按照变异的概率Pm进行变异操作，然后通过赋值（即gen=gen+1）得到新的种群。再根据第②步重新计算。

5 地下物流配送路径优化的算例分析

5.1 案例

现有某个规模较大、运输规模较高的城市A需要建设地下物流系统，以缓解地上物流配送。通过实地考察，未来需要通过地下物流配送线路联结7个主要的物流中心，如图1所示，线段上的数值即为地下物流配送线路的行车距离。假定物流车辆在所有路段上的行车速度均为恒定值20km/h，而且不考虑车辆的起停加减速。为了简便起见，假设任意路段的建设投资成本都为45万元/m，营运成本均为1万元/m，时间成本的权重设定为12元/h，车辆在所有站点停留的时间均为15min。

根据实际所需，现给定了5条可供选择的线路：

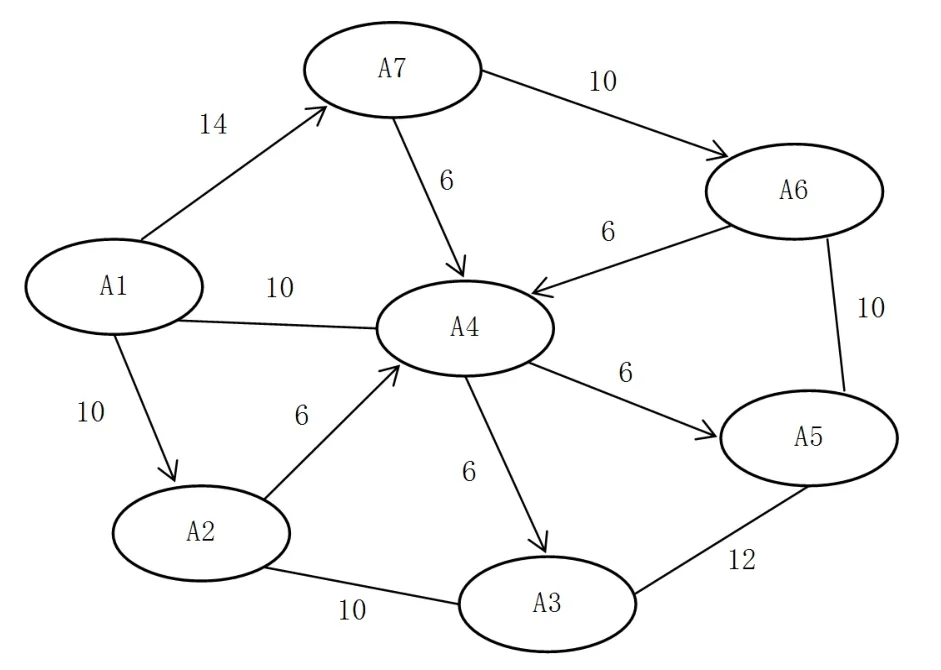
图1 A城市地下物流系统的站点分布情况

①A1→A4→A6；

②A1→A7→A4→A3；

③A1→A2→A4→A5；

④A6→A5→A3→A2；

⑤A7→A6→A4→A3。

同时，结合A城市地下空间可供开发规模，限定地下物流配送的路线总长不宜高于40km。各个物流中心之间货物的流量分布见表1。

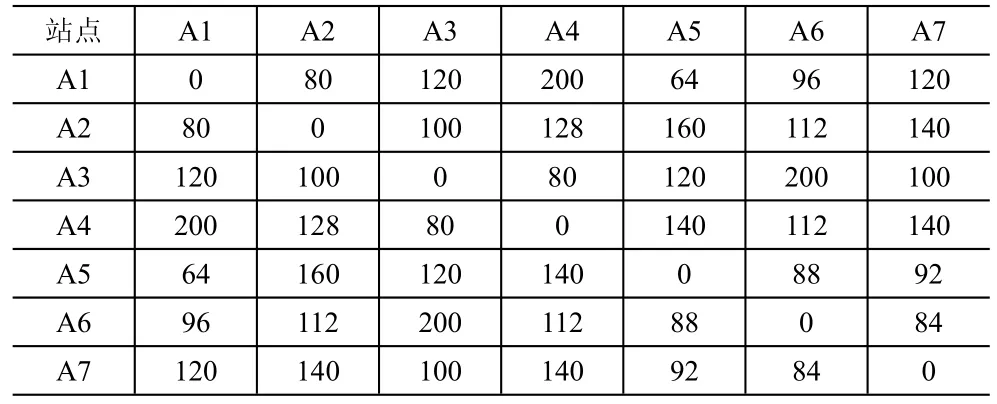
表1 各个站点之间的货物流量表

5.2 优化计算

由于物流配送正反向的路径和货物流量都是相等的，所以这里仅需要考虑单方向的最优路径。根据A城市地下物流系统的站点分布图，可整理得到各个站点之间的距离，见表2。

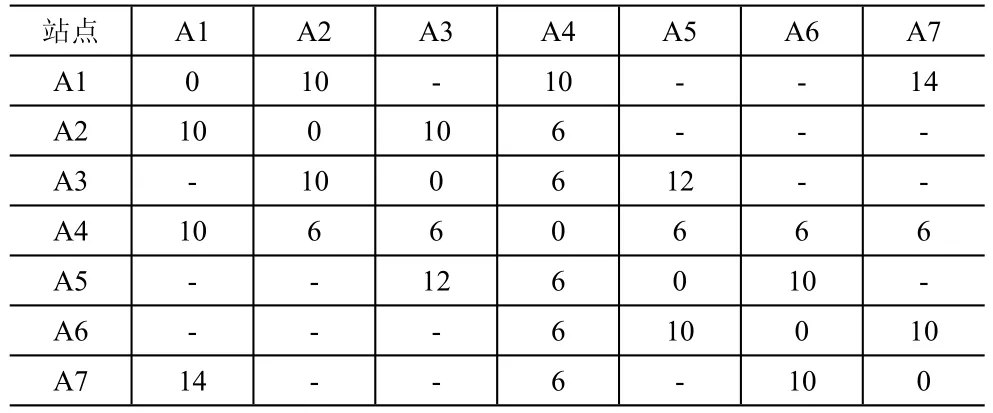
表2 各个站点之间的距离表

根据给定的数据，按照第3节给出的模型，采用第4节设定的0-1编码遗传算法进行计算。由于备选的地下物流配送线路为5条，因此染色体长度为5。根据模型数据需要，取种群数量为200，取交叉率为0.65，取变异率为0.05。

根据0-1编码的步骤进行编程计算，最终得到最优的地下物流配送路径有两条，分别为：

①A1→A2→A4→A5；

②A7→A6→A4→A3。

经检验，发现这两条路径确实是最优的，即算法是可靠的。所以，A城市应根据以上两条路径进行地下物流配送线路建设，以达到最优。

6 结语

与地上物流配送路径优化相比，地下物流配送路径优化有自身的特殊点，在考虑成本优化方面应同时考虑投资成本和时间成本。本文以地下物流配送的总成本最小为目标，对路径优化的模型进行设计，并采用0-1编码的遗传算法进行计算。通过算例，验证了本文提出的模型和计算方法是可行的。而且本文的模型中同时考虑了投资成本和时间成本，对实际过程中的地下物流配送路径规划的应用提供重要的理论依据。但是，本文的模型也有不足之处，主要在于对物流车辆速度、节点停留时间、单位建设成本等做了简单假设，在实际过程中这些变量指标可能存在变动性，因此下一步需要考虑这些因素，对模型进行进一步充实。

[1]马成林,杨学春,董景峰,马超,安立华.基于ANP与模糊TOPSIS的城市地下物流系统集装单元选择决策方法[J].物流技术,2015,(19):110-114.

[2]富文军.城市物流配送系统的优化研究[J].信息技术与信息化,2015,(1):66-68.

[3]富文军.基于遗传算法的物流配送路径优化研究与应用[D].延安:延安大学,2015.

[4]郭兴成,郭美文.基于电子商务的城市物流配送体系优化研究[A].第九届珠三角流通学术峰会—扩大内需与现代流通体系建设论文集[C].2012.

Study on Underground Logistics Distribution Path Optimization with Investment and Time Cost Considerations

Shu Xinting
(Zhejiang University of Finance&Economics,Hangzhou 310018,China)

In this paper,we analyzed the uniqueness of the underground logistics system in relation to the above-ground logistics system,then considering the investment cost and time cost and targeting at the minimal total cost,designed the underground logistics distribution path optimization model and solved it using the 0-1 encoded genetic algorithm.At the end,through a numerical example,we demonstrated the validity of the model and algorithm.

investment cost;time cost;underground logistics distribution;path optimization

F252

A

1005-152X(2016)11-0136-04

10.3969/j.issn.1005-152X.2016.11.029

2016-10-07

舒鑫挺，男，浙江宁波人，浙江财经大学数据科学学院数学与应用数学专业学生，主要研究方向：数学应用。