非线性转子-密封系统动力学行为演变机理研究

李忠刚，陈照波，陈予恕，朱伟东，3，马文生

（1．哈尔滨工业大学机电学院，黑龙江哈尔滨150001；2．哈尔滨工业大学航天学院，黑龙江哈尔滨150001；3．美国马里兰大学机械工程，美国巴尔的摩县21250；4．中航工业集团公司沈阳发动机设计研究所，辽宁沈阳110015）

非线性转子-密封系统动力学行为演变机理研究

李忠刚1，2，陈照波1，陈予恕2，朱伟东2，3，马文生4

（1．哈尔滨工业大学机电学院，黑龙江哈尔滨150001；2．哈尔滨工业大学航天学院，黑龙江哈尔滨150001；3．美国马里兰大学机械工程，美国巴尔的摩县21250；4．中航工业集团公司沈阳发动机设计研究所，辽宁沈阳110015）

旋转机械广泛应用于民用、航空、航天和航海等各个领域，其稳定的动力学行为是保证工程机械安全运行的前提。本文主要针对转子-密封系统丰富的非线性动力学行为，利用非线性动力学等理论分析了转子-密封系统发生Hopf分岔和1∶2亚谐共振等动力学行为的产生条件和机理，进一步给出了非线性转子-密封系统由自激振动引发亚谐共振的动力学行为演变机理，并通过理论分析，阐明了转子-密封系统的气流阻尼和刚度等动力学参数对系统动力学稳定性的影响规律，同时也利用数值计算验证了分析结果。其理论分析结果对实际工程振动分析和结构设计具有一定的理论指导意义。

转子-密封系统；Muszynska气流模型；非线性转子动力学；多尺度法；Hopf分岔；亚谐共振；自激振动；临界转速

转子系统在非线性力作用下的动力学行为非常丰富，因此国内外学者针对非线性转子系统动力学特性做出了大量杰出的工作［1］。在包含非接触式密封的高参数旋转机械系统中由于气体压力、流速和温度等参数较高，端部密封的气流激振力非常复杂，在实际工程中有时会严重影响机组的正常运行［2］。然而对转子-密封系统中气流激振力的实验研究比较困难，目前国内外只有部分学者根据相似性等原理设计了转子-密封系统实验台并进行了相关数据测试［3-5］。在气流激振力模型研究方面，Alford［6］在1965年首先提出了气流激振的力学模型——Alford模型，虽然能很好地解释了气流激振的基本现象，但Alford模型为线性模型。随后，Rosenberg［7］提出了迷宫密封中流体的周向流动会激发出作用于转轴上的扰动循环力。1986年，美国Bently公司的Muszynska［8］在大量转子-密封系统流体实验的基础上，给出了流体激振力描述模型——Muszynska模型。此模型是一个非线性模型，虽然Muszynska模型很好的揭示密封中流体激振力的作用现象，但是其模型中含有多个需要通过实验获得的经验参数，限制了此模型的广泛适用性。在动力学分析方面，丁千等［9］应用Muszynska流体激振力模型建立的单盘转子-密封系统，并利用中心流形定理和正规形理论研究了系统的Hopf分岔和自激振动等非线性动力学产生机理；马辉等［10］应用数值计算的方法研究了转子-轴承-密封系统在两个不同载荷下存在多周期和分岔振动等丰富的动力学特性；何洪军等［11］基于双控体模型研究了转子-密封系统动力学模型；王炜哲等［12］研究了实际工质气体的密封力模型，并数值模拟了单盘转子系统的动力学特性。Hopf分岔理论与多尺度法等动力学理论和方法研究非线性转子-密封系统的周期解特性，并结合数值方法描述转子-密封系统动力学特性，阐明数值计算中的非线性动力学特性的演变规律。

1 转子-密封系统动力学模型及HOPF分岔分析

首先建立Jeffcott转子-密封系统非线性动力学模型，如图1所示，并考虑重力和不平衡质量对转子的作用，系统动力学模型可表示为

式中:M为转子质量，m为气流惯性效应；Ke、De分别为转轴的刚度和外阻尼；K、D为密封中气流激振力的刚度和阻尼，K和D均为位移（x，y）的非线性函数为密封结构经验系数；λ为密封中气流的周向平均流速比，也为位移(x，y)的非线性函数，λ=λ0(1-e)b，b为密封结构经验系数；mg为转子自身重力；ρ为转子平衡质量；r为不平衡质量半径。可见系统（1）为非线性动力学系统，其动力学行为无法用传统的八参数法完全描述。

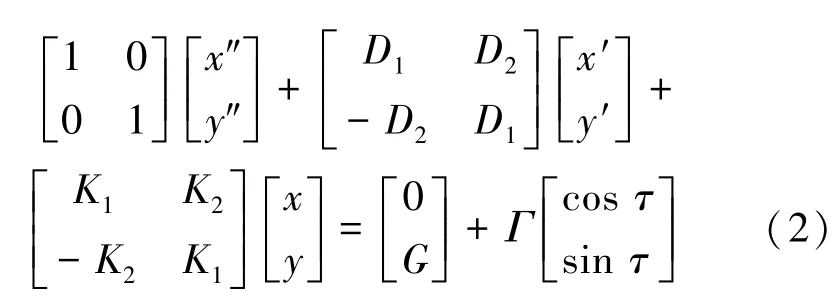
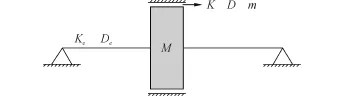
图1 单盘转子-密封结构模型Fig．1 Model of the rotor-seal system

首先将动力学系统（2）可表示成状态方程形式为

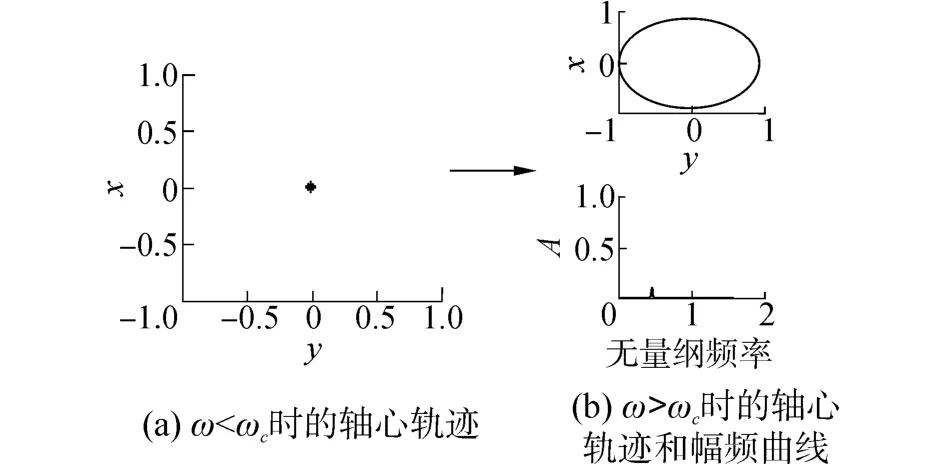
图2 Hopf分岔前后系统状态图Fig．2 Analysis chart of system before and after Hopf bifurcation

2 转子-密封系统1∶2亚谐共振理论分析

在实际工程中，不平衡转子-密封系统会发生由气流激振力诱发的低频振动，导致系统出现1∶2亚谐共振。由于低频振动的突发性和强烈振动（幅值较高），有时会严重影响机组的安全运行，因此对亚谐振动机理的产生研究是非常必要的。首先，将系统（2）在静平衡点领域内进行幂级数展开，得到转子-密封系统在平衡点领域内的幂级数表达形式，再考虑剔除影响较小的高阶非线性项，则可得非自治的转子-密封系统幂级数模型，可表示为

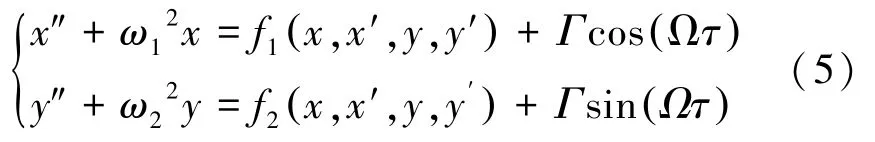
式中:ω1和ω2为系统固有频率和为系统非线性力幂级数展开形式三次截断表达式，Ω为系统外激励频率。

本文采用多尺度法来进一步研究系统（5）的周期解析解特性。设所求一次近似解形式为

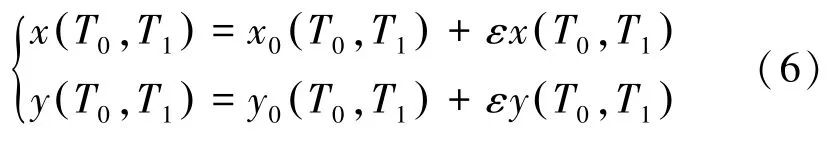
式中:Tn=εnt( n=0，1)为不同尺度的时间变量，T0为快时间变量，T1为慢时间变量。此时关于时间的导数为

将x、x′、x″和y、y′、y″代入动力学系统（5）中，由ε的同次幂系数可得:

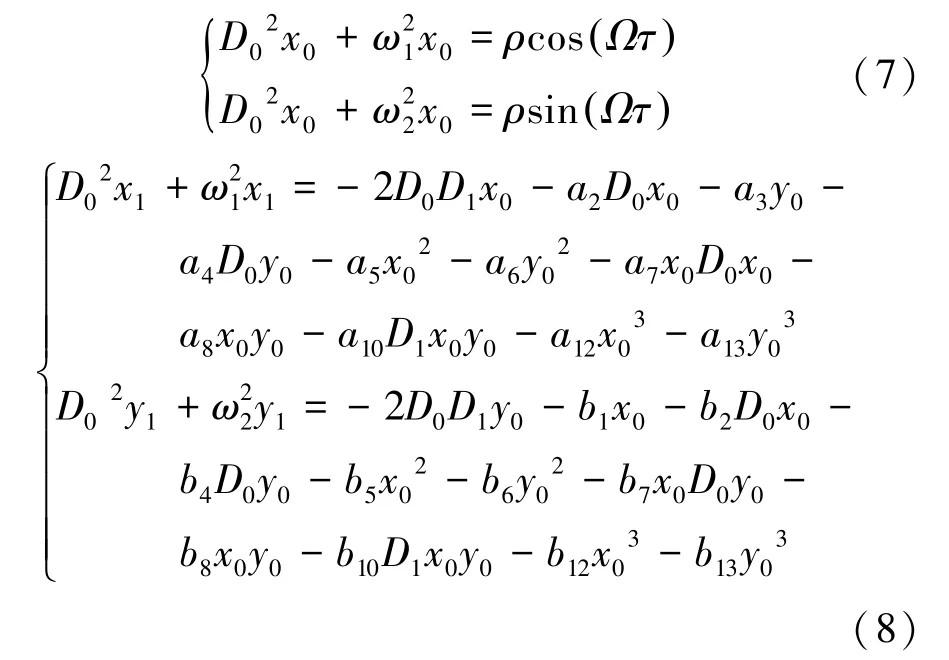
若系统存在1∶2亚谐共振，转子的固有频率ω为外激励频率的一半，即ω=1／2( Ω+σ)，σ为调谐参数。根据方程（7），解可设为

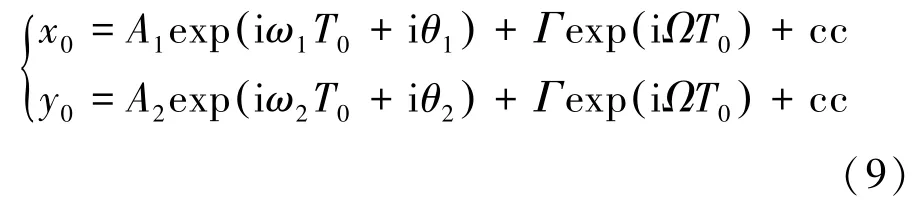
式中:A1、A2为时间变量Tn的函数，cc为前面部分的共轭表达式为激励幅值项。为消除方程（8）中产生的长期项，必有:

可见式（10）中A1，A2的解相同，为分析方便可只分析第一个方程，将式（10）第一个方程的实部和虚部分离可得到:

其中φ=-2θ+2T0σ。由方程（9）消去相角项φ，系统（5）的分岔方程为

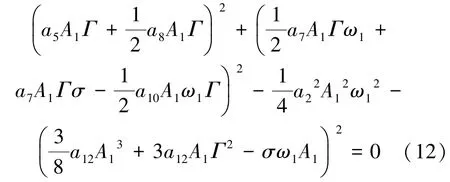
方程（12）非零解存在条件可以表示为

由此可知，由不平衡质量引起的同步周期振动会在非零解参数区域内被诱发出现1∶2亚谐共振。若转子-密封系统不平衡质量很小，气流激振力不会诱发系统出现亚谐共振现象或者可能发生亚谐共振的转速较高；但当系统不平衡质量较大时，气流激振力极易在转子发生同步涡动时会诱发出亚谐振动成分。

3 转子-密封系统非线性动力学演变机理及数值分析

当转速较低时，转子-密封系统在不平衡质量的作用下，只会发生同步运动，如图3所示。且在一阶固有频率下，随着转速的提升振动幅值会明显增加。随着转速升高，系统在临界转速ωc处会出现Hopf分岔，即此时会出现一个自激振动频率成分，但由于自激振动频率和转速频率可能不可约化导致系统出现拟周期运动，同时在Poincaré截面上出现闭合点集，在频谱上能看到两个不可约化频率峰值，如图4所示。随着转速持续增加，系统的自激振动频率会接近系统固有频率，此时两个频率可以约化，系统会出现倍周期运动，如图5所示。此时频谱图上的两个频率成分比值为1∶2。当转速继续增加，系统出现由低频振动产生的极限环，频谱图上低频振动幅值较高，此时系统的振动主要由自激振动已发的系统共振导致，如图6所示，同时可见振动幅值有所增加，有多个频率成分，系统会变得更加不稳定。

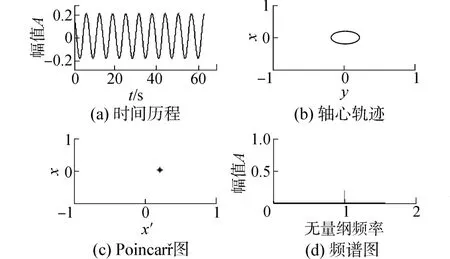
图3 ω=120 rad／s系统分析图Fig．3 Analysis charts of system with ω=120 rad／s

图4 ω=295 rad／s系统分析图Fig．4 Analysis charts of system with ω=295 rad／s

系统的不平衡质量是外激励主要因素，其大小对系统的动力学影响如图7所示。从图中可以看出，当外激励幅值较大时，如图7中Γ=0．4时所示，系统会发生超临界的Hopf分岔行为，即非零解与零解分别出现在Hopf分岔点的两侧；当外激励幅值减小后，如图7中Γ=0．18时所示，系统发生亚临界Hopf分岔行为，即非零解与零解出现在Hopf分岔点附近的同一侧；当外激励幅值再进一步减小后，如图7中Γ=0．1时所示，系统会在分岔点附近发生振动幅值跳跃的现象，且会存在两个不同的振动幅值，此时系统会发生倍周期运动。外激励幅值大小会改变系统发生亚谐振动的临界转速阈值，随着外激励幅值的减少，发生亚谐共振的转速会随之增加，由式（13）也可知系统亚谐振动非零解的起始点与外激励幅值大小有关。综上可知，转子系统在进行了较好的动平衡后，在恒定工作转速附近不易出现亚谐共振。但如果转子-密封系统在运行过程中发生其他动力学参数改变可能会导致系统临界转速降低或系统转速持续提高等，在动平衡较好的转子-密封系统上一旦产生亚谐振动，其振动幅值将会增加较快，甚至会发生跳跃现象，导致系统不稳定。在工程实际中，汽轮机组曾经出现过:一旦机组发生由气流激振引起的亚谐共振，系统振动幅值将会突然增大，短时间内就导致系统严重的失稳现象。

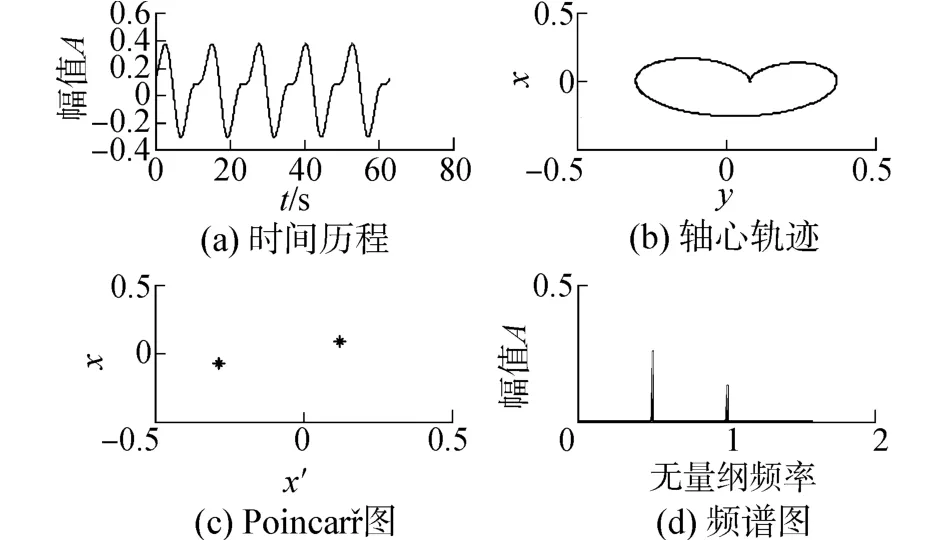
图5 ω=310 rad／s系统分析图Fig．5 Analysis charts of system with ω=310 rad／s

图6 ω=470 rad／s系统分析图Fig．6 Analysis charts of system with ω=470 rad／s

20世纪90年代，美国Texas大学Iwatsubo等［14］开展了大量实验，通过改变密封结构增加气流阻尼来抑制气流激振，但实验结果非常不理想。根据系统分岔方程（12），得到了系统在不同非线性刚度系数下，气流阻尼对系统发生亚谐振动位置的影响，如图8所示。不同的气流激振力阻尼会导致系统发生亚谐振动的转速不同；但是当非线性刚度发生变化后，气流阻尼对动力学系统分岔点（临界转速）的影响也会不同，甚至可能会出现相反的作用效果。如图8所示。因此可见转子-密封系统中气流阻尼对系统分岔点的影响，需要根据系统其他动力学参数而确定。

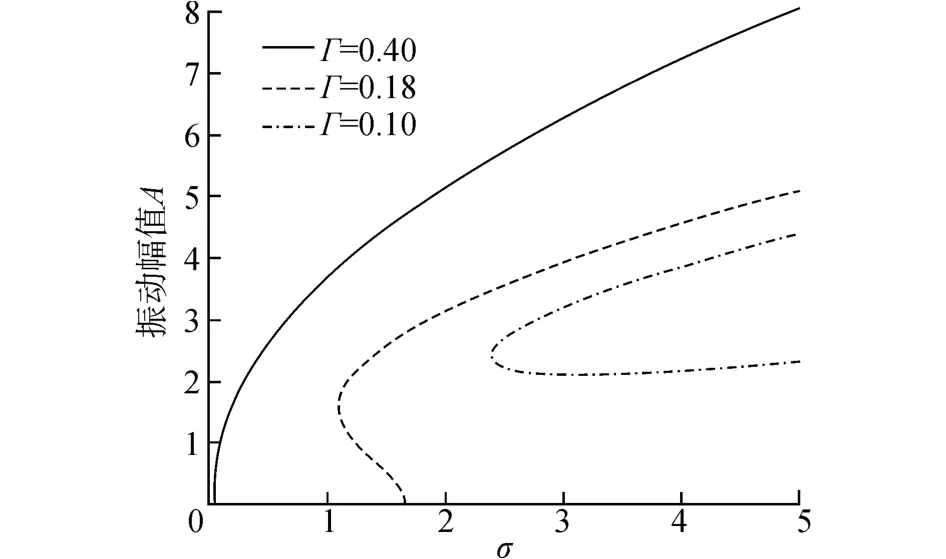
图7 外激励幅值对系统的影响Fig．7 Effect of the exitation amplitude on the system

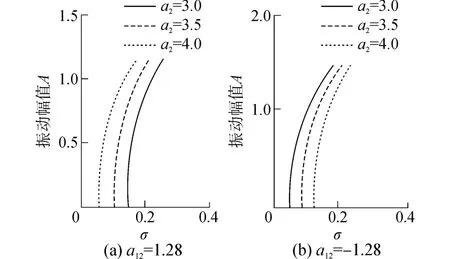
图8 气流阻尼对系统的影响Fig．8 Effect of the gas damping on the system

4 结论

1）本文建立了转子-密封系统非线性动力学模型，根据Hopf分岔条件，给出转子-密封系统发生周期解失稳的临界转速计算公式，通过计算公式可知密封激振力对系统动力学显著；

2）进一步应用非线性振动中的多尺度方法研究转子-密封系统动力学解析解表达式，由平均方程获得了转子-密封系统分岔方程；

3）由分岔方程获得了系统非零解的判断条件，即发生Hopf分岔和1∶2亚谐共振产生条件，阐明了转子-密封系统非线性动力学产生机理；

4）利用数值计算方法详细阐明了转子-密封系统的自激振动与亚谐共振动力学行为演变规律；

5）根据转子-密封系统分岔方程理论分析了气体阻尼增加未必会增加系统稳定性的原因，此理论分析结果与美国Texas大学实验结论一致。

本文的分析结果对实际工程振动分析和设计具有一定的理论指导意义。

［1］黄文虎，武新华，焦映厚，等．非线性转子动力学研究综述［J］．振动工程学报，2000，13（4）:497-509．HUANG Wenhu，WU Xinhua，JIAO Yinghou，et al．Review of nonlinear rotor dynamics［J］．Journal of vibration engineering，2000，13（4）:497-509．

［2］DIMAROGONAS A D，GOMEZ-MANCILIA J C．Flow-excited turbine rotor instability［J］．International journal of rotating machinery，1994，1（1）:37-51．

［3］MARQUETTE O R，CHILDS D W，SAN ANDRES L．Eccentricity effects on the rotordynamic coefficients of plain annular seals:theory versus experiment［J］．Journal of tribology，1997，119（3）:443-447．

［4］曹浩，杨建刚，郭瑞，等．密封动力特性系数试验识别方法及影响因素分析［J］．机械工程学报，2011，47（9）:85-89．CAO Hao，YANG Jiangang，GUO Rui，et al．Experimental identification method and influence factor analysis of seal dynamic characteristic［J］．Journal of mechanical engineering，2011，47（9）:85-89．

［5］KWANKA K．Dynamic coefficients of stepped labyrinth gas seals［J］．Journal of engineering for gas turbines and power，2000，122（3）:473-477．

［6］ALFORD J S．Protecting turbomachinery from self-excited rotor whirl［J］．Journal of engineering for power，1965，87（4）:333-343．

［7］ROSENBERG C．Investigating aerodynamics transverse force in labyrinth seals in case involving rotor eccentricity．C．E．Tran．083［J］．Translated from Energnmashinostrojohic，l974，8:15-17．

［8］MUSZYNSKA A．Whirl and whip—rotor／bearing stability problems［J］．Journal of sound and vibration，1986，110（3）:443-462．

［9］DING Q，COOPER J E，LEUNG A Y T．Hopf bifurcation analysis of a rotor／seal system［J］．Journal of sound and vibration，2002，252（5）:817-833．

［10］MA Hui，LI Hui，NIU Heqiang，et al．Nonlinear dynamic analysis of a rotor-bearing-seal system under two loading conditions［J］．Journal of sound and vibration，2013，332（23）:6128-6154．

［11］何洪军，荆建平．非线性转子-密封系统动力学模型研究［J］．振动与冲击，2014，33（10）:73-76．HE Hongjun，JING Jianping．Dynamic model of a nonlinear rotor-seal system［J］．Journal of vibration and shock，2014，33（10）:73-76．

［12］WANG Weizhe，LIU Yingzheng，JIANG Puning．Numerical investigation on influence of real gas properties on nonlinear behavior of labyrinth seal-rotor system［J］．Applied mathematics and computation，2015，263:12-24．

［13］李忠刚，孔达，焦映厚，等．转子-密封系统非线性动力学特性分析［J］．振动与冲击，2009，28（6）:159-163．LI Zhonggang，KONG Da，JIAO Yinghou，et al．Research on nonlinear dynamic characteristics of a rotor-seal system［J］．Journal of vibration and shock，2009，28（6）:159-163．

［14］IWATSUBO T，FUKUMOTO K，MOCHIDA H．An experimental study of dynamic characteristics of labyrinth seal，NASA CP-3239［R］．NASA，1993:219-238．

Study on the mechanism and transformation of the dynamic behavior in a nonlinear rotor-seal system

LI Zhonggang1，2，CHEN Zhaobo1，CHEN Yushu2，ZHU Weidong2，3
（1．School of Mechatronics Engineering，Harbin Institute of Technology，Harbin 150001，China；2．School of Astronautics，Harbin Institute Technology，Harbin 150001，China；3．University of Maryland，Mechanical Engineering，Baltimore County 21250，USA；4．AVIC Shenyang Aeroengine Research Institute，Shenyang 110015，China）

Rotating machinery is widely used in civilian，aviation，aerospace，navigation，and other fields，and the stability behavior of the system dynamics is a prerequisite guaranteeing safe operation．In this paper，by using nonlinear dynamics theories，complicated transformation of the dynamic behaviors，Hopf bifurcation and 1∶2 sub-harmonic resonance，was investigated on a rotor-seal system，and the conditions and mechanism of the dynamic behavior were obtained．Furthermore，the evolution of subharmonic resonance dynamics in the nonlinear rotor-seal system caused by self-excited vibration was analyzed．Based on the theoretical analysis，it is observed that the damping and stiffness parameters of the nonlinear rotor-seal system affect its system stability dynamics．Finally，numerical calculation verifies the results from the theoretical analysis．It is significant that the results of the theoretical analysis can explain the vibration behavior of the system and guide the structural design of the system in practical engineering．

rotor-seal system；Muszynska′s gas model；nonlinear rotor dynamics；multiscale method；Hopf bifurcation；sub-harmonic resonance；self-excited vibration；critical speed

10．11990／jheu．201510041

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．006．html

O347．6

A

1006-7043（2016）12-1704-05

李忠刚，陈照波，陈予恕，等．非线性转子-密封系统动力学行为演变机理研究［J］．哈尔滨工程大学学报，2016，37（12）:1704-1708．

2015-10-19．

2016-09-28．

国家自然科学基金项目（11302058；11272100）；中国博士后面上基金项目（2013M541360）．

李忠刚（1982-），男，助理研究员，博士．

李忠刚，E-mail:lizhonggang＠hit．edu．cn．

LI Zhonggang，CHEN Zhaobo，CHEN Yushu，et al．Study on the mechanism and transformation of the dynamic behavior in a nonlinear rotor-seal system［J］．Journal of Harbin Engineering University，2016，37（12）:1704-1708．