云环境下的高效K-Medoids并行算法

李媛媛，孙玉强，晁 亚，刘 阳

(1.常州大学 信息科学与工程学院,江苏 常州 213164； 2.中国电建 上海电力环保设备制造总厂有限公司,上海 201900)

云环境下的高效K-Medoids并行算法

李媛媛1，孙玉强1，晁 亚1，刘 阳2

(1.常州大学 信息科学与工程学院,江苏 常州 213164； 2.中国电建 上海电力环保设备制造总厂有限公司,上海 201900)

传统聚类算法K-Medoids对初始点的选择具有随机性，容易产生局部最优解；替换聚类中心时采用的全局顺序替换策略降低了算法的执行效率；同时难以适应海量数据的运算；针对上述问题，提出了一种云环境下的改进K-Medoids算法，该改进算法结合密度法和最大最小原则得到优化的聚类中心，并在Canopy区域内对中心点进行替换，再采用优化的准则函数，最后利用顺序组合MapReduce编程模型的思想实现了算法的并行化扩展；实验结果表明，该改进算法与传统算法相比对初始中心的依赖降低，提高了聚类的准确性，减少了聚类的迭代次数，降低了聚类的时间。

云环境；K-Medoids聚类；Canopy算法；最大最小原则；MapReduce

0 引言

随着数据规模的爆炸性增长，传统的数据挖掘工作在处理大规模数据时会出现用时过长、存储量不足等缺点。云计算的提出将这些问题迎刃而解，它是一种基于互联网的计算，是分布式计算、并行处理和网格计算的进一步发展。由Google提出的MapReduce编程框架[1]是云计算中代表性的技术，主要用于海量数据的并行计算。已有多种数据挖掘算法在MapReduce计算模型的基础上被实现了，而聚类是在数据挖掘中运用比较广泛的一种算法。

K-Medoids算法是一种典型的基于划分的聚类算法[2]，该算法[3]简单且易于实现，运用于科学研究的各个领域。但是它对初始聚类中心的选择非常敏感，不能有效地对大规模数据进行聚类处理。针对K-Medoids算法的特点以及不足，国内外很多学者提出了相应的改进K-Medoids算法。文献[4]提出了一种基于 MapReduce 的 K-Medoids 并行算法，用并行模型高效快速地对海量数据进行聚 类处理，但并没有解决K-Medoids算法对初始中心敏感的问题。文献[5]提出一个基于最小支撑树的聚类中心初始化方法，对估计密度方面的方法进行了改进，但是增加了时间复杂度；文献[6]对初始中心点进行优化，并在每个簇内对中心点进行替换，提高了算法的效率，但降低了聚类的精确度；文献[7]提出一个基于初始中心微调与增量中心候选集的改进 K-Medoids 算法，文献[8]提出一种基于密度初始化的改进算法，这些研究通过不同的方法解决了算法对初始中心敏感的问题和对中心点替换的策略进行优化，但无法适应海量数据的处理需求。文献[9]提出一种基于ACO的K-Medoids聚类算法；文献[10]提出一种基于粒计算的 K-Medoids聚类算法，都是结合一些成熟的算法来改进K-Medoids聚类算法，虽然在少量数据环境下能够显著提升算法的性能，但却因为额外的组件增加了算法的复杂性。

因此，本文提出了一种云环境下的高效K-Medoids并行算法，其结合了密度思想和最大最小原则对初始中心点优化以提高聚类效率；通过在Canopy区域内进行中心点替换来降低时间复杂度；并利用云计算对改进K-Medoids算法进行进一步研究以提高该改进算法的并行化执行速度。实验表明，该并行化的改进算法将具有重要的理论研究价值和实际应用意义。

1 MapReduce简介

MapReduce是一种分布式并行编程模型，数据被存储在分布式文件系统(distributed file system, DFS)中，以键-值对的形式来表示数据。MapReduce的具体步骤是：先将数据切割成Split，对Split又分成一批键值对传给Map函数；Map函数对每个键值对进行处理后形成新的键值对< K2,V2>，并把K2值相同的进行汇总，输出中间结果< K2,list>；Reduce函数对Map函数输出的中间结果做相应的处理后得到键值对。MapReduce的操作流程如图1所示[11]。

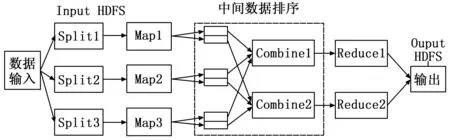
图1 Mapreduce的操作流程图

2 传统K-Medoids算法介绍和分析

传统K-Medoids算法思想[4]：在包含n个数据对象的数据集D中，首先随机选择k个不同的数据对象作为初始聚类中心Oi；再根据其剩余数据对象到聚类中心的相似度(欧式距离)，将其分配给与之相似度最大(距离最近)的中心点所在的聚类；然后全局随机选取一个非聚类中心点的数据对象p作为替代簇心；如果替代簇心的聚类效果比当前簇心好，则更新当前的簇中心，继续进行聚类迭代，直到各簇中心不再发生变化，说明当前聚类结构不再进行调整，迭代算法结束。判定一个非中心点对象比当前中心点效果好的参照是误差平方和准则函数的值减少，即用非中心点p代替中心点Oi的代价S<0。

欧式距离公式如下：

(1)

其中：i=(xi1,xi2,...,xip)；j=(xj1,xj2,...,xjp)分别表示一个p-维数据对象。

误差平方和函数可以定义为：

(2)

其中：p为类Ci中的样本，Oj为聚类中心(p和Oj均是多维的)。

传统的K-Medoids算法通过完全随机的策略对初始聚类中心点进行选取，不能确保聚类结果的准确性。可以通过密度思想和最大最小原则相结合的策略求得数据集的初始聚类中心。

在高密度区域选择初始中心点可以排除噪声点和孤立点的干扰，而最大最小原则可以避免在高密度区域选取的中心点过于邻近，具体表述如下。

定义1：高密度点：取数据集中的数据对象xi为中心点，计算此中心点在邻域半径δ内包含的样本个数，若样本个数不少于常数Minds，则该中心点就被称为高密度点。其中δ的取值需结合输入的数据对象集，将其取为n个数据样本间距离均方根的一半，公式如下：

(3)

其中：║xi-xj║为公式(1)的欧式距离D(i,j)。

得到优化的初始中心点流程为：

1)根据定义3计算出原始数据集的高密度点，并将其放于集合S{X1,X2,…Xn}中。从中取最高密度点作为第一个初始聚类中心点C1，并将其从S中删除；

2)在剩余的高密度点集S中找到距离C1最远的点，作为第二个初始聚类中心点C2，并将其从S中删除；

3)分别计算剩余高密度点集到已有的i个聚类中心点之间的距离，取最小距离的最大者：D(i+1)=max{min{D(j,1),D(j,2),…,D(j,i)}}，j=1,2,…,n，则第i+1个初始聚类中心点为Ci+1=Xj，并将其从S中删除；

4)当表示D(i+1)变化幅度的深度指标Depth(k)=|D(k)-D(k-1)|+ |D(k+1)-D(k)|取得最大值时，所得到的前k个记录值就是需要的初始聚类中心点，同时下一轮Canopy的区域半径可设为T1=D(k)，避免了Canopy算法初始值设置的盲目性和随机性。

3 K-Medoids算法的改进思想

1)K-Medoids算法时间复杂度较高，不能很好的处理大规模数据的聚类操作。而基于MapReduce的分布式并行计算模型，将一个大型数据切分成多个小数据模块的形式，分配给多台计算机集群进行分布式计算，与传统的单机运行平台相比，加快了总体的运行速率，减少了执行时间。

2)传统的K-Medoids算法在对聚类中心进行替换时，采用的是全局顺序替换的策略，虽然在一定程度上确保了聚类的效果，但是总体上降低了算法的效率，而且全局顺序替换策略不能适应大规模数据的聚类处理。对于一个中心点，若要对其进行替换，一些较优的候选点最有可能出现在该中心点附近，如同一簇内或其附近簇中的点。因此在搜索新的中心点时可以只在这些范围内进行。对此，提出了一种Canopy(华盖)区域内中心点随机替换策略来代替传统的替换方法，即在每个Canopy区域内部对中心点进行随机替换。基于Canopy区域的中心替换策略是Park等人[6]提出的簇内替换策略的优化扩展，扩大了搜索的范围，提高聚类精度。

3)传统的K-Medoids算法将剩余数据对象分配给距离最近的簇时，计算了剩余数据对象与每一个中心点的距离，使得计算规模较大。而通过Canopy的粗略划分后，只需要计算剩余数据对象与对应的同一Canopy区域内的中心点之间的距离，降低了运算规模，提高运行效率。

Canopy算法[12]的思想是使用一种代价低的相似性度量方法，快速粗略地将数据划分成若干个重叠子集，每个子集可以看成是一个簇。Canopy划分基本流程如下：(1)设置阈值T1=D(k)，Canopy中心为上一轮的k个初始聚类中心点；(2)计算剩余的数据集中每一个数据对象与所有的Canopy中心之间的距离，如果该数据对象与某个Canopy中心的距离在T1内，则将该对象加入到这个Canopy中，当该数据对象与所有Canopy中心的距离计算完成后，将其从数据集中删除，如果该数据对象没有加入到任何Canopy，则构建一个新的Canopy。

4)传统算法都是将聚类内部的数据对象的距离误差平方和作为准则函数，没有考虑到所有聚类之间的距离对聚类总体质量的影响。对此，为了得到最优的空间聚类结果，提出了一种基于加权的准则函数[8]。

类间距离b定义为不同聚类中心点间的距离，可以表述为：

(4)

基于加权的准则函数采用类内距离w(即公式(2)的误差平方和函数)和类间距离b共同决定，则准则函数可以表示为：

(5)

其中：w1、w2为加权系数，且w1+w2=1；w1、w2需要根据不同的数据集设置，但w1、w2必须满足w1+w2=1的关系，使聚类效果达到最好并能提高算法的适应性。

4 改进算法的并行化描述

4.1 改进算法基本流程

首先运用密度思想和最大最小距离法相结合的方法求得数据集的初始聚类中心；再在聚类中心的替换方法上，用Canopy区域内随机替换策略代替传统的全局顺序替换策略，以改进K-Medoids算法。一方面，该算法可以通过获得优化的初始聚类中心来提高聚类结果的精确度；另一方面，该算法能够提高收敛速度，降低时间复杂度。最后，将改进后的算法运用于MapReduce的并行计算模型中，其基本流程如图2所示。

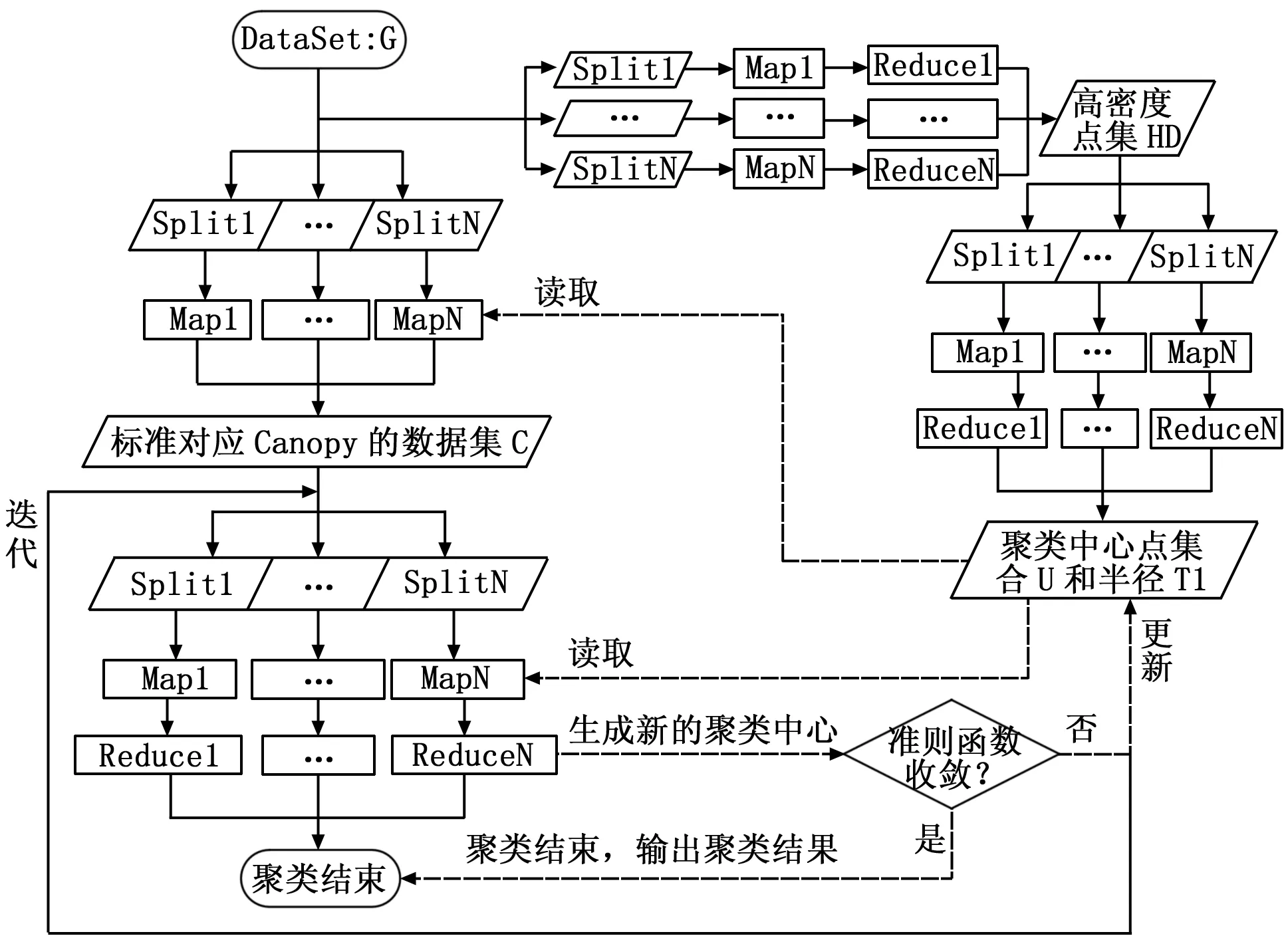
图2 基于Mapreduce的改进K-Medoids算法的基本流程图

4.2 改进算法并行化步骤

4.2.1 计算初始聚类中心点

计算高密度数据集

算法1：高密度点的生成

输入：数据集S

输出：高密度点集H

Map函数：

每个Map读取数据集S，计算每个数据点xi与其余数据点之间的距离Di,j；

Reduce函数:

1)根据公式(3)计算邻域半径δ，并统计到每个数据点xi距离小于δ的数据个数；

2)读取密度阈值Minds，若个数大于Minds，则把该点定义为高密度点，得到高密度点集合H。

3)最大最小原则计算初始中心点

该阶段任务确定初始中心点[13]以及区域半径T1，避免了下一个阶段Canopy算法初始值设置的盲目性和随机性，具体算法如下：

算法2:中心点生成算法

Map 函数:

输入：高密度点集H

输出：中心点的初始集合Q

1)设置初始中心点的集合，Q=null；

2)设置迭代次数，Whilek< sqrt(N)(当前节点数据规模N)；

3)if集合Q为空，求数据集V(当前节点数据集V)中密度最大点，并保存该点至集合Q；else求数据集V中数据点与集合Q中数据点的距离最小值中最大者，并保存该点至集合Q；

Reduce 函数:

输入：各节点中心点的初始集合Q={Q1,Q2,...,Qn}；

输出：中心点的最终集合U以及半径T1；

1)求取集合Q的数据总量，N=Count(Q) ；

2)设置迭代次数，Whilek< sqrt(N)

3)求数据集中数据点之间距离最小值中最大者，并保存该点至集合Q′；

4)求取集合Q′的数据量m= Count(Q′)；

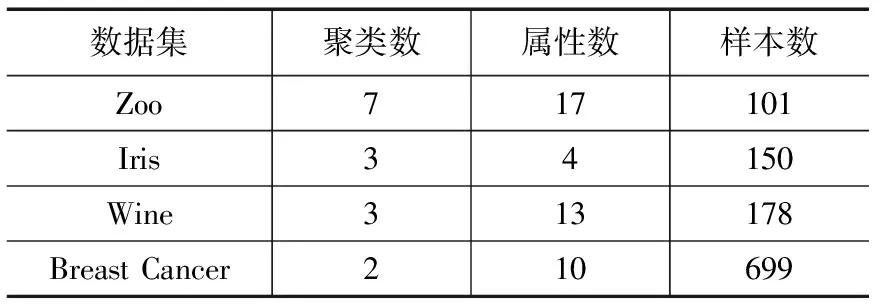
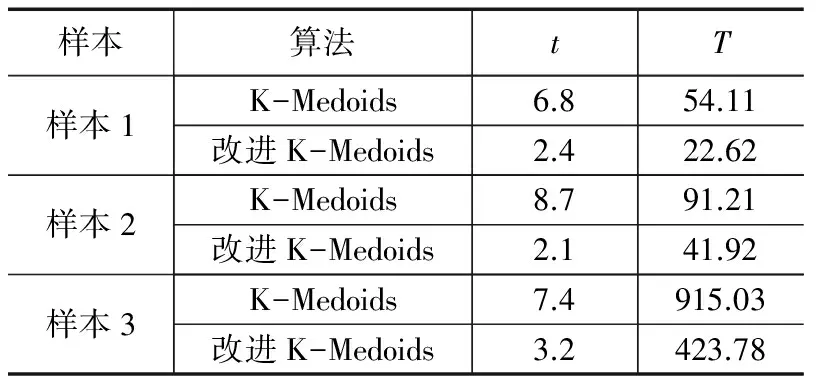
5)whilej

4.2.2 Canopy划分

算法3：Canopy划分算法

Map函数:

输入：数据集S

输出：标注对应Canopy的数据集C。

1)读取中心点的最终集合U以及半径T1，计算数据集中的对象与中心点之间的距离D；

2)当D≤T1，则标注该数据点属于对应的Canopy，并将结果输出。

4.2.3 K-Medoids迭代

该阶段的主要任务是进行精确的聚类计算，其算法流程为：

算法4：K-Medoids算法

输入：标注对应Canopy的数据集C

输出：K中心点集合U′

Map 函数:

1)读取中心点的最终集合U，将中心点的最终集合U作为初始K中心点集合，U′=U；

2)通过Map函数比较已标注的输入数据点与对应中心点的距离，输出当前数据点及对应最近距离的中心点编号；

Reduce 函数:

1)通过K个Reduce函数将同一中心点下的数据点归并，在该中心点Oi对应的Canopy内选择一个未被选择过的非中心点p，根据公式(5)计算用p代替Oi的代价并记录在Si中，直到Canopy中所有的非中心点都被选择过；

2)如果Si中最小值小于0，则将最小值对应的非中心点代替当前簇心，进行下一轮MapReduce的迭代，否则终止程序。

5 实验结果分析

5.1 实验平台

硬件环境：6台主机：一台Namenode，5台Datanode；CPU 为2.66 GHz；硬盘为250 G；内存为2 G。

Hadoop集群软件环境：Ubuntu12.04操作系统；VMware Workstation v8.0；Hadoop版本为0.20.2；JDK版本为JDK1.6。

5.2 聚类质量以及执行效率的分析

在Hadoop集群上，采用标准数据集：Zoo、Iris、Wine及Breast Cancer数据集进行聚类研究，分别对K-Medoids算法、改进K-Medoids算法进行测试。

表1 各数据集的参数比较

预先给出K-Medoids算法需要的聚类数目。平均查准率为p，平均查全率为R，迭代次数为t，执行时间为T，以下的结果是运行5次的平均结果。为了能体现改进算法与传统的K-Medoids算法在并行化的条件下的优越性，使用相同 Hadoop集群、相同数据集进行聚类，聚类结果如表2～表5所示。

表2 算法在Zoo数据集的聚类质量以及执行效率

表3 算法在Iris数据集的聚类质量以及执行效率

表4 算法在Wine数据集的聚类质量以及执行效率

表5 算法在Breast Cancer数据集的聚类质量以及执行效率

由表2、表3、表4和表5可以得出以下结论，在处理4种不同类型的数据集时，改进K-Medoids算法不仅聚类效果较K-Medoids算法好，而且具有较快的收敛速度。密度思想和最大最小原则相结合的方法能够快速地获取到较好的初始聚类中心，从而减少算法中的循环迭代次数，加快收敛速度。针对聚类数与属性数相对较多的Zoo数据集，其改进效果更加明显，而对于Breast Cancer这种聚类数较少的数据集能够维持其原来的聚类效果，验证了改进算法在聚类效果上的稳定性。

5.3 K-Medoids聚类加速比分析

增加Iris数据集数据对象的数量，选取样本1、样本2、样本3这3个记录数n(单位：万)分别是1、10、100的数据进行实验对比分析，执行效率如表6所示。在节点数为1、2、3、4、5、6的Hadoop平台上，使用改进K-Medoids算法进行聚类计算所对应的加速比，如图3所示。

表6 算法在不同规模Iris数据集的执行效率

图3 Hadoop下不同规模数据集的改进K-Medoids算法加速比

由表6和图3可以看出：1)在处理样本量较小的数据集时，改进算法的加速比容易达到瓶颈；2)加速比随着节点数的增加而增大，但由于节点数的增加而带来了消耗更多时间的数据通信等使得加速比的增长速度降低；3)在处理大规模的样本集时，改进算法的加速比更趋近于线性。

6 结束语

在处理海量数据时，为解决K-Medoids算法在进行聚类运算时，会出现初始聚类中心选取的不确定性、算法时间复杂度较高、算法的执行效率低下等问题，提出了一种高效的改进K-Medoids算法。为提高算法的执行效率，并在MapReduce的平台下对该改进聚类算法进行实现。并通过实验对其进行对比分析，与传统的聚类算法相比，该改进算法不仅能提高算法的查准率和查全率以及运行效率而且能改进聚类的效果，这对促进 K-Medoids 算法的发展与应用具有积极的意义。

[1] Dean J, Ghemawat S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113．

[2] Han J, Kamber M．数据挖掘：概念与技术[M]．范 明，孟小峰，译．2 版．北京：机械工业出版社，2007．

[3] Chen X Q，Peng H，Hu J S. K-medoids substitution clustering method and a new clustering validity index method[A].Proc of 6th World Congress on Intelligent Control and Automation[C].2006：5896-5900.

[4] 张雪萍，龚康莉，赵广才．基于MapReduce的K-Medoids并行算法[J]．计算机应用，2013, 33(4):1023-1025,1035．

[5] Gao D Y，Yang B R. An improved K-medoids clustering algorithm[A].Proc of the 2nd International Conference on Computer and Automation Engineering(ICCAE)[C].2010：132-135.

[6] Park H S，Jun C H. A simple and fast algorithm for K-medoids clustering[J]．Expert Systems with Applications，2009, 36(2): 3336-3341.

[7] 夏宁霞，苏一丹，覃 希．一种高效的K-medoids 聚类算法[J]．计算机应用研究, 2010, 27(12): 4517-4519．

[8] 姚丽娟，罗 可，孟 颖．一种新的K-medoids聚类算法[J]．计算机工程与应用，2013, 49(19): 153-157．

[9] 孟 颖，罗 可，姚丽娟，等．一种基于ACO的K-medoids聚类算法[J]．计算机工程与应用，2012, 48(16): 136-139．

[10] 马 箐，谢娟英．基于粒计算的K-medoids聚类算法[J]．计算机应用，2012, 32(7): 1973-1977.

[11] Isard M, Budiu M, Yu Y, et al. Dryad: Distributed data-parallel programs from sequential building blocks[A]. Proc. of the 2ndEuropean Conf. on Computer Systems (EuroSys)[C]. 2007: 59-72．

[12] 孙吉贵，刘 杰，赵连宇．聚类算法研究[J]．软件学报，2008, 19(1): 48-61．

[13] 毛典辉．基于MapReduce的Canopy-Kmeans改进算法[J]．计算机工程与应用，2012，48(27)：22-26．

Highly Efficient Parallel Algorithm of K-Medoids in Cloud Environment

Li Yuanyuan1, Sun Yuqiang1, Chao Ya1, Liu Yang2

(1.School of Information Science&Engineering，Changzhou University，Changzhou 213164，China； 2.SEPEE，Power Construction of China，Shanghai 201900，China)

Traditional K-Medoids clustering algorithm selects the initial points randomly, which is easy to produce local optimum; when replace the cluster centers, adopted global sequential replacement policy reduces the efficiency of the algorithm; at the same time, it is difficult to adapt to operation of massive data. In response to the above problems, an improved K-Medoids clustering algorithm in cloud environment is proposed. The algorithm combines the density method and Max-Min principle to obtain optimized cluster centers, and replaces centers in the area of Canopy, and adopts optimization criterion function, and finally uses the ideas of sequential composition of MapReduce programming model to achieve the parallel extensions of the algorithm. Result of the experiments shows that the improved method is less dependent on the initial points and reduces the number of iterations and the clustering time.

cloud environment; K-Medoids clustering; Canopy algorithm; max-min principle; MapReduce

2016-07-20；

2016-08-02。

国家自然科学基金项目(11271057,51176016)；江苏省自然科学基金项目(BK2009535)。

李媛媛(1991-)，女，江苏盐城人，硕士研究生，主要从并行计算、数据挖掘等方向的研究，CCF学生会员ID方向的研究。

孙玉强(1956-)，男，河南人，教授，硕士研究生导师，主要从事并行计算、软件工程等方向的研究。

1671-4598(2016)12-0139-04

10.16526/j.cnki.11-4762/tp.2016.12.040

TP311

A