水下滑翔机附加质量数值计算

杨 磊，曹军军，姚宝恒，曾 铮，连 琏

(上海交通大学 船舶与海洋工程国家重点实验室，上海 200240)

水下滑翔机附加质量数值计算

杨 磊，曹军军，姚宝恒，曾 铮，连 琏

(上海交通大学 船舶与海洋工程国家重点实验室，上海 200240)

水下滑翔机的附加质量对其运动状态影响较大，本文采用了 Hess-Smith（面元法）方法编制了计算任意三维物体附加质量的程序，利用 Gambit 软件对水下滑翔机进行网格划分，计算出实验室所研制的水下滑翔机附加质量，同时利用 CFD（Computational Fluid Dynamics）技术，结合动网格技术和 UDF（User-Defined Function），对水下滑翔机进行了 PMM（Planar Motion Mechanism）试验模拟，并与 Hess-Smith 方法得到的结果进行对比，分析两者之间的特点和各自优势。

附加质量；水下滑翔机；面元法；PMM

0 引 言

水下滑翔机是通过改变自身重心和净重力来进行水下运动，本身没有外部推进装置。它具有低能耗、低成本、适应性强等特点，进而可以完成长期大范围的调研任务。它在物理海洋、生物海洋等领域具有广泛的应用空间[1]。

随着国内外对深潜器研究不断深入，对其操纵性预报要求越来越高，而潜器的惯性力水动力可由附加质量进行推算，因此精确的附加质量计算对深潜器的设计十分重要。国内外对附加质量进行了大量的研究，目前获取附加质量有以下几种方法，对于规则形状物体的附加质量可以利用图谱进行查找[2]，对于复杂物体的附加质量可以使用 Hess-Smith 方法[3]，以求解出物体无升力绕流场的数值解。此外，也可以通过实验的方式得到物体的附加质量，但其成本较高，适用范围窄。随着计算流体力学的飞速发展，CFD 方法也逐渐成为预报附加质量的有效方法。在船舶领域、潜艇领域、水陆两栖车领域[4-6]等均有该方法的使用。但目前对水下滑翔机附加质量的研究较少，多数文献采用简化模型近似求解甚至直接使用相似滑翔机的结果，对运动仿真造成一定的偏差。

为了精确求解实验室所研制的水下滑翔机附加质量，本文使用了 Hess-Smith 方法设计程序，同时利用Gambit 软件对水下滑翔机表面进行网格划分，获取滑翔机表面节点信息，导入程序中求解矩阵从而得到结果；同时，本文利用 CFD 软件对水下滑翔机的 PMM试验进行模拟，利用动网格技术实现网格时时更新，UDF 实现了对滑翔机纯垂荡运动、纯横荡运动、纯首摇运动和纯俯仰运动 4 种运动控制，通过对所受到的力和力矩的分析处理，得到附加质量。通过对比 Hess-Smith 法和 CFD 方法得到的附加质量，验证了本文使用的 2 种计算方法可行性和准确性，进而对比两者之间各自优劣，为对以后从事相关计算的人员提供参考意见和方法。

1 基于面元法的附加质量计算

1.1 基本方程和边界条件

在不可压缩势流中，定常速度势（Φ）在物体外部空间域中适合拉普拉斯方程，在物面上适合不可进入条件，在无穷远处，应与均匀来流的速度势吻合。在速度势 Φ 中分出已知的均匀来流项，即可得到扰动速度势 φ 的定解条件：

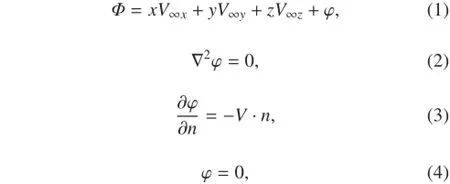
其中：式（2）在物体外部；式（3）在物体表面上；式（4）在无穷远处；V 为物体运动速度，n 为物面单位法线向量，指向物体内部。

1.2 速度势离散

假设流场中的场点 p（x, y, z），物面上的源点为q，在物面上布置强度为 σ（q）的 Rankine 源，则流场内任意点的速度势为

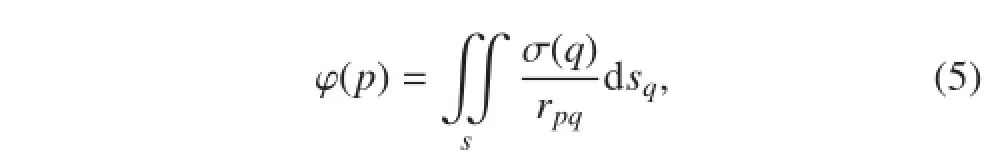
其中：rpq为场点 p 和源点 q 之间的距离；s 为物面。

在式（5）两端取法向导数，并令点 p 沿法线方向趋于物面上的点。式（5）右端分布源的法向导数由两部分组成，一部分是 P 点附近小曲面 ε 贡献的，另一部分是物面其他部分 s-ε 贡献的。同时代入式（3）的边界条件，可以得到：

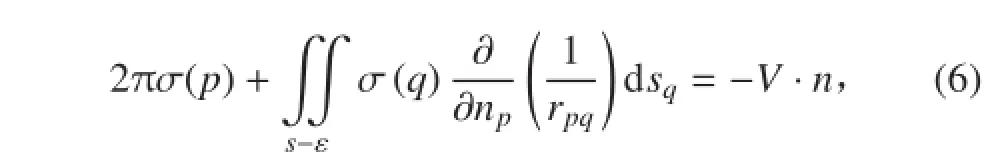
将积分式（6）转换成线性代数方程组，即把物面s 分成 N 小块，小块形状可为三角形或四边形，近似代替小曲面（Δsj）。本文采用三角形划分，利用右手法则进行编号，得到单位向量，再通过三角形平均中心点进行投影，得到新的三角形 ΔQj代替原来的小曲面。因此，物面 s 上的积分可以用 N 个三角形上的积分之和近似，即：

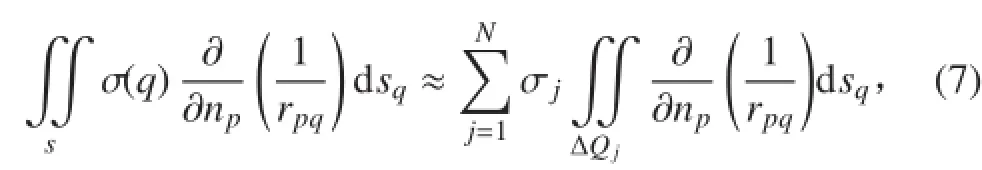
将式（7）代入式（6）中，可以得到 σ 的 N 阶线性代数方程组：

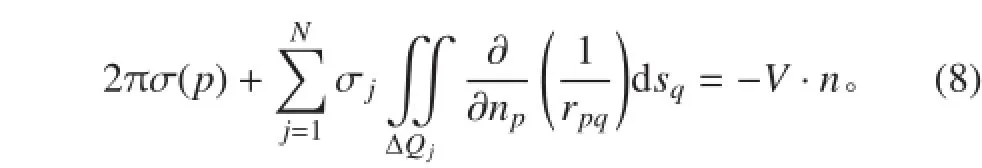
动点 p 是 N 个单元的中心点，通过 Gambit 软件，对物体进行网格划分，导出网格数据后，将节点信息导入程序中，即可求解出 σj的值，再通过式（5）得到速度势 φ。本文将水下滑翔机表面进行网格划分，其中网格为三角形，共计 907 个，利用各网格节点坐标生成近似图，观察网格划分质量，如图 1 所示。

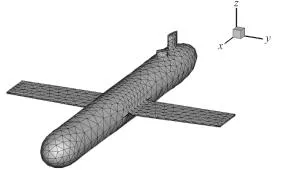
图 1 水下滑翔机三角形网格划分Fig. 1 The generation of triangular mesh for an underwater glider

1.3 附加质量求解

当一个刚体在理想流体中做非定常运动时，会带动周围流体做加速运动，其所受到的流体力的大小与运动加速度成正比，方向则与加速度方向相反，这个比例系数即为附加质量 λij。一个任意形状的物体运动时，会产生 36 个附加质量。

根据势流理论[7]，可知：

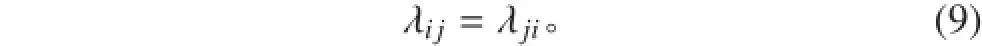
由于水下滑翔机相对于 xoz 平面左右对称，则附加质量中所有 i + j 为奇数的系数全部为 0。同时，本滑翔机机翼相对于 xoy 平面对称，仅尾部上端布置了天线和平衡舵，因此相对于 xoy 平面是大致上下对称的，则 λ13和 λ15很小，可以忽略。因此附加质量的矩阵形式为：

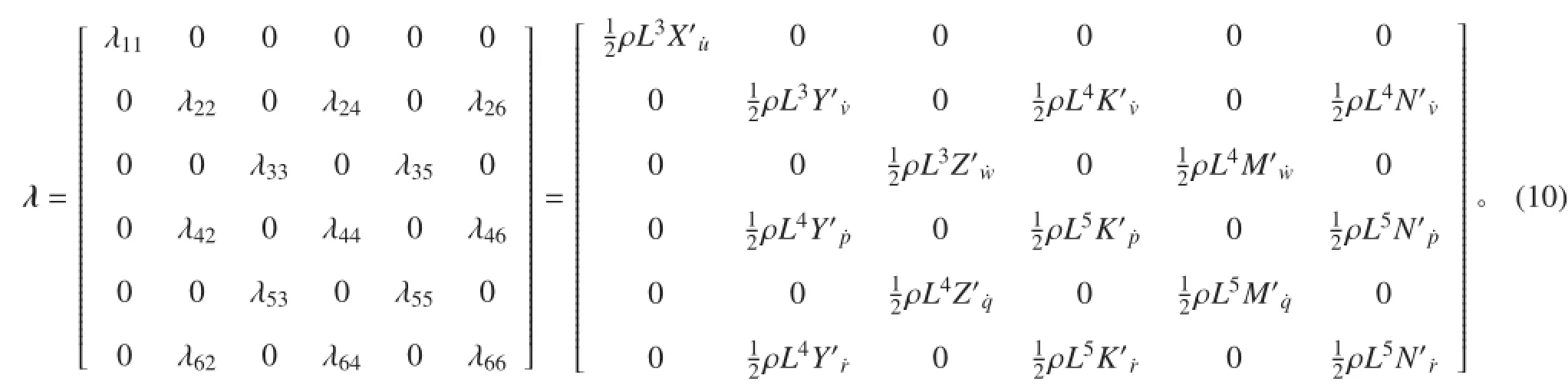
按照势流理论知物体附加质量为：

式中，i, j=1, 2……6, φ1,2,3分别为刚体沿动系坐标轴 x, y, z 以单位速度平动时引起的流体速度势，φ4,6,6则分别为刚体以单位角速度绕 x, y, z 轴以单位角度转动时所引起的流体速度势。因为扰动速度势 φ 已得，因此可求出物体的附加质量。

本文对水下滑翔机进行了网格划分，同时使用Fortran 软件编写程序，将网格节点信息导入后，即可得到水下滑翔机附加质量结果，如表 1 所示。

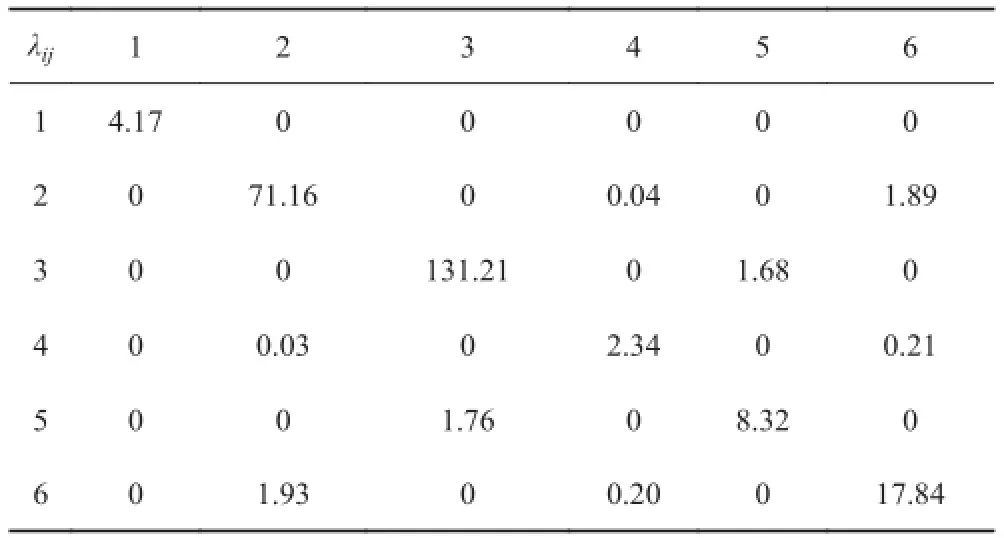
表 1 水下滑翔机附加质量Tab. 1 The added mass of an underwater glider

2 基于 CFD 软件的附加质量计算

Fluent 软件可提供动网格技术，动网格模型可以用来模拟流程形状由于边界运动而随时间改变的问题，利用 UDF 可以定义边界的运动方式。本文则是对水下滑翔机进行 PMM 试验模拟，从而得到附加质量。

2.1 计算方程

水下滑翔机 PMM 试验主要包括：纯升沉运动、纯横荡运动、纯俯仰运动、纯摇首运动[8]。由于纯升沉运动与纯横荡运动类似，纯俯仰运动与纯摇首运动类似，本文仅写出前两者的运动方程和处理方法。

对于纯升沉运动，其运动方程为：

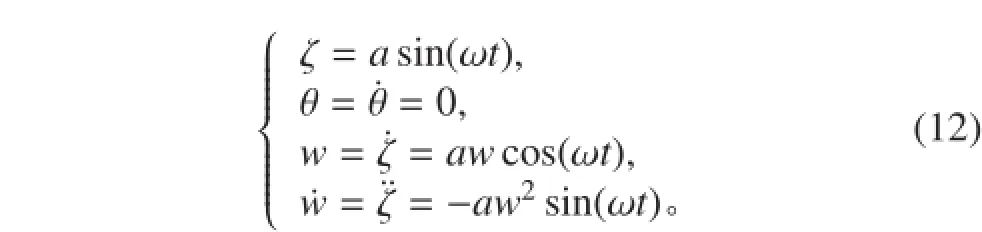
其中：ζ 为滑翔机垂向位移；a 为滑翔机纯升沉运动的振幅；分别为水下滑翔机纵倾角度和角速度；分别为水下滑翔机垂向速度和加速度。根据运动方程可知，滑翔机做纯升沉运动的轨迹如图 2 所示。

图 2 水下滑翔机纯升沉运动示意图Fig. 2 The heaving motion of an underwater glider

根据水动力系数的含义可得到方程：

式中：Z 为运动过程中滑翔机受到的垂向力；M 为绕 y轴的力矩。

对于纯俯仰运动，其运动方程为：

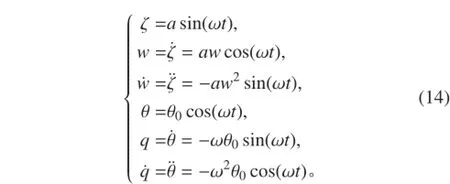
式中：θ0为滑翔机纯俯仰运动纵倾角振幅，q 为角速度。

根据运动方程可知，滑翔机做纯俯仰运动的轨迹如图 3 所示。为了满足纯俯仰的运动条件，即模型纵轴时时保持与原点轨迹相切，可得到方程：

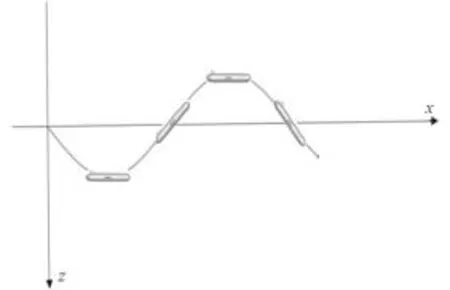
图 3 水下滑翔机纯俯仰运动示意图Fig. 3 The pitching motion of an underwater glider

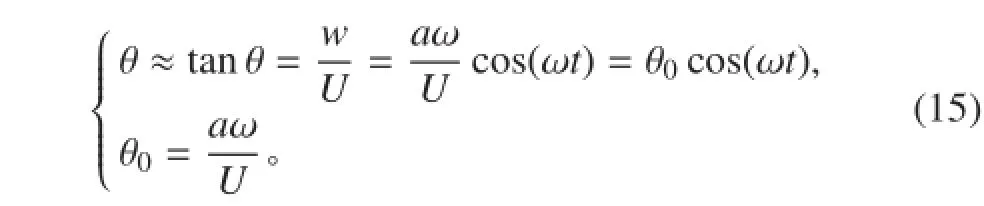
因为滑翔机的 PMM 试验为小振幅运动，因而可以近似处理，其中，U 为滑翔机 x 方向上的来流速度。

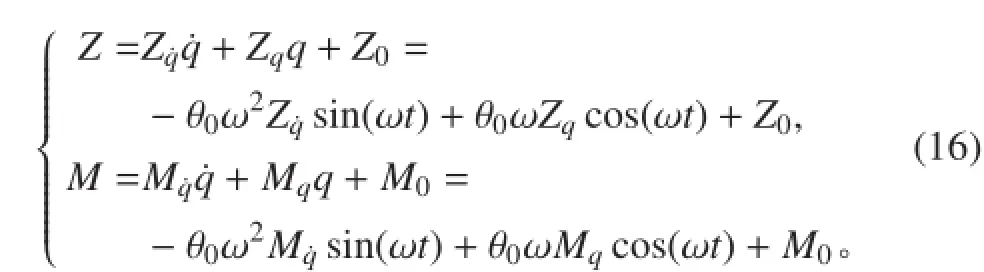
2.2 CFD 计算准备

精确的计算结果和高质量的网格密不可分，由于水下滑翔机外形较为复杂，而四面体网格具有较好的贴体性，适应各类复杂形体，同时结构化网格质量高，网格数量少，结果精确，节省运算时间。因而将计算域分为内域和外域 2 个部分，内域采用非结构网格，而外域采用结构化网格。兼得两者的优点，减少计算时间，提高精度。

图 4为计算内、外域网格划分和边界条件说明图，网格总数量约为 260 万，其中入口边界给定为VELOCITY_INLET，出口边界为 OUTFLOW，水下滑翔机表面设为 WALL，壁面设为 VELOCITY_INLET 且速度与入口边界相同。

湍流模型选取 SST k-ω 模型，压力速度耦合选取SIMPLEC 算法，压力插值采取 Standard 格式，动量、湍动能和湍流耗散率插值采用 Second Order Upwind格式。

在 Fluent 软件中，需要编制以描述水下滑翔机运动的用户自定义函数（UDF），本文根据水下滑翔机PMM 试验所对应的运动方程如式（12）和（14）来编制 UDF 程序，其中 DEFINE_CG_MOTION 函数控制滑翔机的运动，COMPUTE_FORCE_AND_MOMENT 函数用于得到滑翔机每一时刻的力和力矩，并通过FPRINTF 函数记录和存储在文件中。

2.3 结果处理与分析

以纯升沉运动为例，设定振幅 a = 300 mm，来流速度 v = 0.3 m/s，滑翔机长度为 L = 2 m，海水密度 ρ = 1 025 kg/m3。为了使迭代时间歩长取整数，频率 f 设置为：0.2, 0.4, 0.5, 0.625。以 f 为 0.4 时为例，周期是 2.5 s，因此 fluent 中设置计算步长为 0.01 s，每个周期需要250 步完成，计算 3～5 个周期后结束，利用数据的结果，在 Origin 软件中进行处理。取时间靠后结果较为稳定的数据进行拟合，如图 5 和图 6 所示。

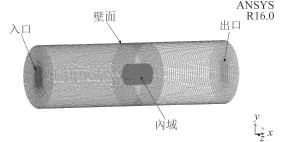
图 4 计算域内域和外域网格划分Fig. 4 The mesh of internal and external flow domain

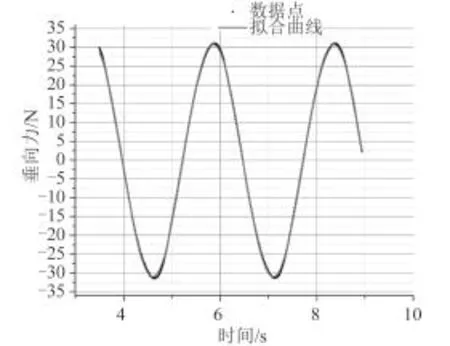
图 5 纯升沉运动 f = 0.4 时垂向力 Z 的变化Fig. 5 The changes of force in Z-direction when the frequency of heaving motion is 0.4

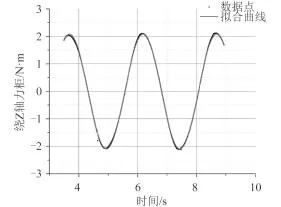
图 6 纯升沉运动 f = 0.4 时绕 Z 轴力矩的变化Fig. 6 The changes of moment around Z-direction when the frequency of heaving motion is 0.4

Origin 软件具有自定义拟合函数的功能，利用式（13）编写出相应的拟合函数，从而得到高精度的拟合结果。

当 f = 0.4 时，得到拟合力和力矩的曲线函数为：

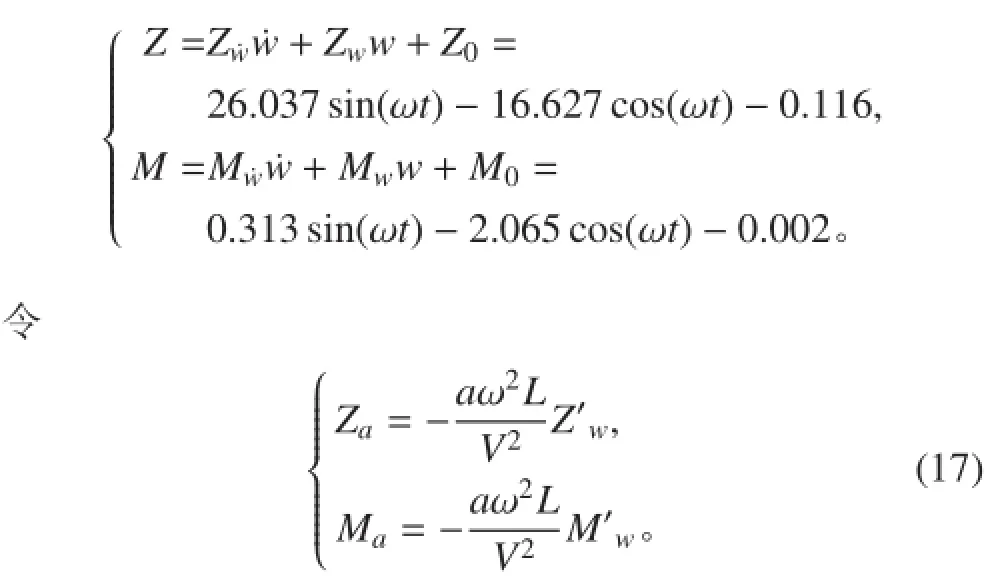
通过计算多个频率下的纯升沉运动，并进行曲线拟合，最终可以得到如表 2 所示的结果。

根据表 2 的结果，通过最小二乘法拟合得到无因次的加速度系数，如图 7 所示。

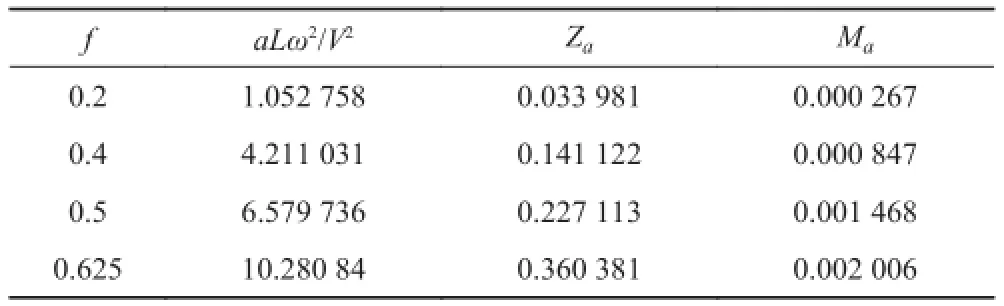
表 2 纯升沉运动拟合结果Tab. 2 The fitting results in heaving motion

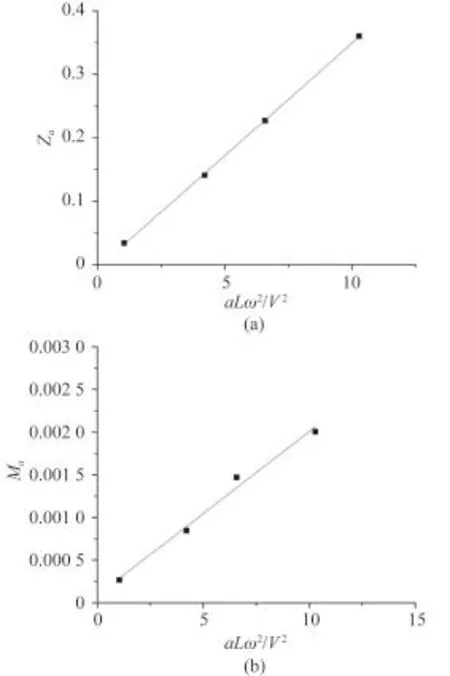
图 7 利用最小二乘法计算加速度系数Fig. 7 The acceleration coefficients applying the least square method

类似于纯升沉运动，可以得到其他几组运动的结果，结果如表 3 和表 4 所示。

通过表 3 和表 4 可见，使用 PMM 试验模拟结果与利用面元法得到的结果之间差别较小，最大误差小于11%，满足实际工程需求。

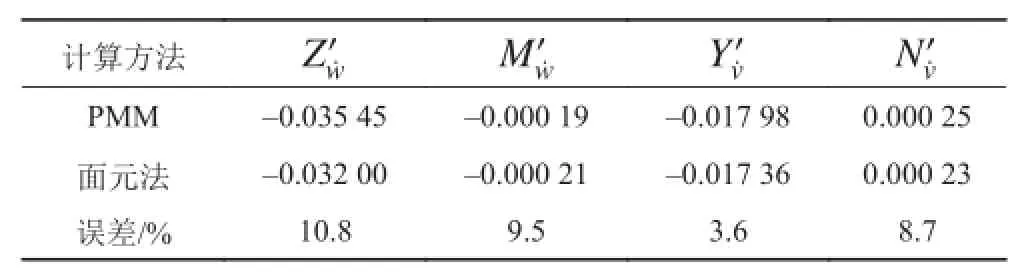
表 3 纯升沉和纯横荡运动结果Tab. 3 The results in heaving and swaying motions

表 4 纯俯仰和纯摇艏运动结果Tab. 4 The results in pitching and yawing motions

3 结 语

本文通过面元法编写程序得到水下滑翔机附加质量，同时结合 PMM 试验原理，利用 Fluent 软件和动网格技术，得到给定运动下的水动力和力矩，从而得到水下滑翔机的惯性水动力系数，通过对计算结果分析，可以得到：

1）对于水下滑翔机，Hess-Smith 面元法程序和Fluent 仿真得到的附加质量结果均比较精确，满足工程需求。

2）相比于 Fluent 软件仿真需要花费较多时间多次建模与计算，Hess-Smith 方法仅需要重新划分物体的面网格，节省大量时间，但编写程序较为复杂。

3）本文提供了计算水下滑翔机附加质量的 2 种方法，介绍了两者原理与优劣，同时得到精确的附加质量，验证了 2 种方法的可行性和准确性，对水下滑翔机的水动力设计和运动仿真具有重要指导意义和参考价值。

[1]ZHANG S W, YU J C. Spiraling motion of underwater gliders: modeling, analysis, and experimental results[J]. Ocean Engineering, 2013, 60: 1–13.

[2]孟凡豪. 50 kg级水下自航行器整体水动力学性能优化设计[D]. 杭州: 中国计量学院, 2014: 56–57. MENG Fan-hao. Shape optimization design of 50 kilograms autonomous underwater vehicle based on hydraulic characteristics[D]. Hangzhou: China Jiliang University, 2014: 56–57.

[3]林超友, 朱军. 潜艇近海底航行附加质量数值计算[J]. 船舶工程, 2003, 25(1): 26–29. LIN Chao-you, ZHU Jun. Numerical computation of added mass of submarine maneuvering with small clearance to sea-bottom[J]. Ship Engineering, 2003, 25(1): 26–29.

[4]杨勇, 邹早建, 张晨曦. 深浅水中KVLCC船体横荡运动水动力数值计算[J]. 水动力学研究与进展, 2011, 26(1): 85–93. YANG Yong, ZOU Zao-jian, ZHANG Chen-xi. Calculation of hydrodynamic forces on a KVLCC hull in sway motion in deep and shallow water[J]. Chinese Journal of Hydrodynamics, 2011, 26(1): 85–93.

[5]孙铭泽, 王永生, 张志宏, 等. 基于网格变形技术的全附体潜艇操纵性计算[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(2): 420–424. SUN Ming-ze, WANG Yong-sheng, ZHANG Zhi-hong, et al. Numerical simulation of submarine maneuverability based on mesh deformation technology[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2013, 37(2): 420–424.

[6]黄劲, 余志毅, 刘朝勋, 等. 基于CFD的两栖车辆水动力导数的计算方法[J]. 车辆与动力技术, 2014(2): 39–43. HUANG Jin, YU Zhi-yi, LIU Chao-xun, et al. Numerical method for hydrodynamic coefficients of an amphibious vehicle based on CFD[J]. Vehicle & Power Technology, 2014(2): 39–43.

[7]马骋, 连琏. 水下运载器操纵控制及模拟仿真技术[M]. 北京:国防工业出版社, 2009. MA Cheng, LIAN Lian. Maneuvering control and simulation technology of underwater vehicles[M]. Beijing: National Defense Industry Press, 2009.

[8]张晓频. 多功能潜水器操纵性能与运动仿真研究[D]. 哈尔滨:哈尔滨工程大学, 2008: 25–26. ZHANG Xiao-pin. Research on maneuverability and motion simulation of multifunction vehicle[D]. Harbin: Harbin Engineering University, 2008: 25–26.

Numerical method for added mass of an underwater glider

YANG Lei, CAO Jun-jun, YAO Bao-heng, ZENG Zheng, LIAN Lian
(Naval Architecture and Ocean Engineering National Laboratory, Shanghai Jiaotong University, Shanghai 200240, China)

Added mass of an underwater glider is quite important for the motions of glider. In this paper, the added mass of an arbitrary three-dimensional body is obtained through Hess-Smith method. Then an underwater glider which was designed by our laboratory is meshed by Gambit software in order to obtain its added mass. Besides, the Planar Motion Mechanism (PMM) tests of the glider are simulated by using CFD software, dynamic mesh technique and UDF. By comparing with the Hess-Smith results, the characters and advantages of Hess-Smith method and PMM are analyzed.

added Mass；underwater glider；Hess-Smith；PMM

U661.33；P715.5

A

1672–7619(2016)12–0116–05

10.3404/j.issn.1672–7619.2016.12.023

2016–05–23；

2016–06–12

国家自然科学基金资助项目(51279107；41527901)；上海市科委项目基金资助项目(13dz1204600)

杨磊(1993–)，男，硕士研究生，研究方向为水下航行器水动力分析及仿真。