EGM2008模型在地形测量RTK高程转换中的应用
符 阳,符永好
(1. 海口市土地测绘院,海南 海口570125)
EGM2008模型在地形测量RTK高程转换中的应用
符 阳1,符永好1
(1. 海口市土地测绘院,海南 海口570125)

对于缺乏高程控制点的测区,在确保成果精度的前提下,以EGM2008模型高程异常代替实际高程异常,推导出了大比例尺地形测量RTK高程转换的近似公式及其精度估计公式,并对高程测量限差m、实际高程异常短波部分的平均变化率q和作业距离限制d三者间的关系进行了深入分析。结果表明,在缺乏高程控制点的测区,在作业距离限制范围内开展大比例尺地形测量时,直接利用EGM2008模型进行RTK高程转换,其结果精度能满足有关规范的要求,无需开展更多的水准测量或三角高程测量工作。
EGM2008模型;RTK;地形测量;高程转换
为减少高程测量繁重的工作量,文献[1]、[2]介绍了在测区内及周边只有少量高程控制点的情况下,采用GNSS单点精确定位、直接利用EGM2008模型和少量高程控制点校准的方法探讨了测区GNSS控制网和RTK碎部测量的高程转换问题。EGM2008模型的阶次完全至2 190,空间分辨率约为9 km或5',与我国大陆东部地区GPS(A/B级网)水准高程异常比对结果:最小值为-1.111 m、最大值为1.252 m、均值为0.060 m、标准差为±0.360 m、均方差为±0.361 m[3]。造成较大差值的主要原因有3 点:①EGM2008模型与我国东部地区实际重力场在分辨率方面存在一定差异,模型建立的分辨率不够详细,忽略了分辨率大于5'(约9 km)的局部重力场短波部分;②无法利用我国分布均匀的实际高程异常控制点进行校准;③EGM2008模型所表示的全球似大地水准面与我国的国家高程基准面存在偏差。正是由于EGM2008模型与我国的实际似大地水准面存在较大偏差且起伏(变化率)很不均匀,若不论测绘精度要求、测区地势状况和RTK基站与流动点的距离长短,简单地将EGM2008模型应用于控制网或小测区大比例尺地形测量的高程转换,很难得出预期满意的结果。本文针对(由于各种原因造成)没有可用的网络RTK和精化似大地水准面模型,只有少量平面(≤3 个)和高程(≤2个)控制点的小测区(以下简称乏控测区),在保证满足规范、成果精度和尽量减少工作量的前提下,较深入地研究了如何利用EGM2008模型开展大比例尺地形测量单基站RTK高程转换的方法。
1 基于EGM2008模型的RTK高程转换方法
1.1 转换方法
设基站点为O、流动点为P,其相应的大地高、正常高、高程异常、EGM2008模型高程异常分别为:Ho、ho、ζo、ξo和Hp、hp、ζp、ξp,则P点正常高的计算公式为:
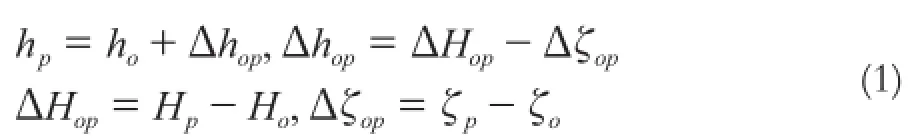
若ho、ζo、ζp为已知,Ho和Hp可由RTK测量直接得到,则由式(1)可计算流动点的正常高。本文假设所有点的实际高程异常为未知,讨论以EGM2008模型高程异常代替实际高程异常的情形。设地面某点的实际高程异常ζi由中长波部分ζiGM和短波部分ζiDM组成,相应的EGM2008模型高程异常ξi也由中长波部分ξiGM和全球大地水准面与我国国家高程基准偏差ξoo(常数)两部分组成,且同一点的ζiGM与ξiGM相等,则对于基站点和流动点有:
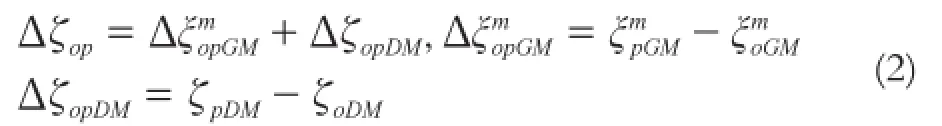
若Ho和Hp由RTK测量直接获得,其绝对值不准确,但其差值ΔHop较准确,以RTK测量得到基站点和流动点的WGS84大地经纬度计算得到的EGM2008模型高程异常值代替实际高程异常,由式(1)、(2)可计算流动点的正常高差为:
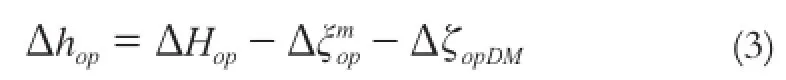
若忽略实际高程异常短波部分的差分值ΔζopDM,则流动点的近似正常高差为:
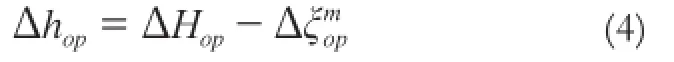
若ho为已知,则由式(1)、(4)可计算流动点的近似正常高。
1.2 ΔζopDM的逼近分析
对于基站点和流动点分别有实际高程异常和EGM2008模型高程异常之差,即δζo=ζo-ξo和δζp=ζpξp,由式(2)得出两点间高程异常之差的差分(起伏)为:

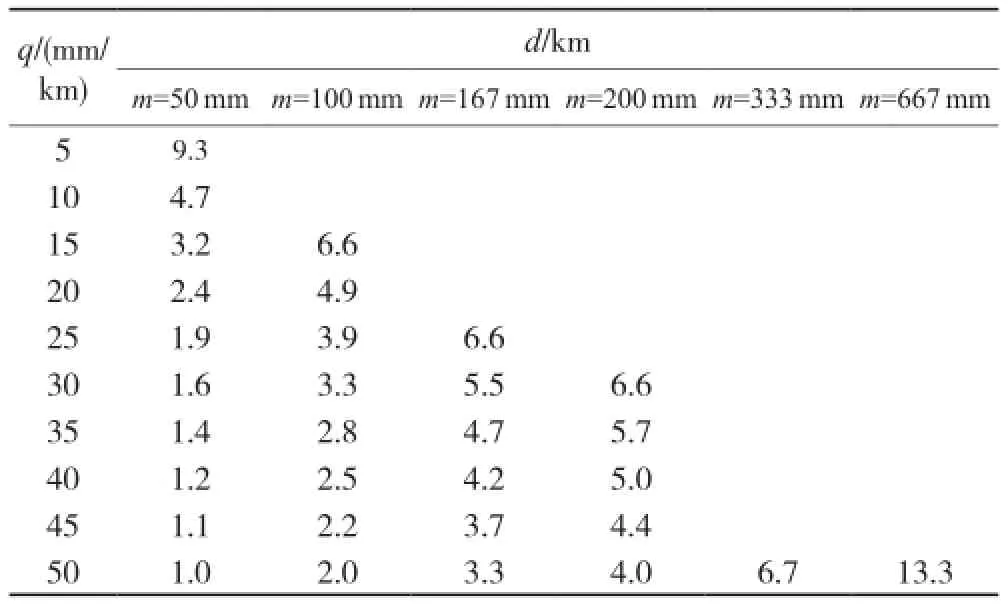
式(5)说明上述两种高程异常之差的差分(起伏)实质为实际高程异常短波部分的差分ΔζopDM。实际高程异常短波部分(即实际高程异常-EGM2008模型高程异常)等值线图的垂直增大方向就是其值变化最大的方向,设这个方向上的平均值(平均变化率)为q(mm/ km),那么其差分值大小可由q与基站点和流动点间距d(km)及其夹角a来逼近。q值越大,表示等值线越密、地势越陡峭;q值越小,表示等值线越稀、地势越平坦。表1是海南省部分市县实际高程异常短波部分起伏特征指标q,其中最大值为等值线最密集处的平均值,最小值为等值线最稀疏处的平均值。制作等值线图用到的GPS水准点实际高程异常数据取自文献[4]的相关资料;EGM2008模型高程异常数据由文献[4]提供的GPS水准点大地坐标计算得到,分辨率至1'×1',具体计算方法参照文献[5]。从表1可以看出:
1)海口市和临高县大部分地区以及陵水县少部分地区q值均很小,即q≤20 mm/km,这些地区的地势特点是平原。
2)海口市和临高县少部分地区以及三亚市的海岸狭窄地带q值均较小,即20 3)三亚市和陵水县大部分地区q值范围是30 表1 实际高程异常短波部分起伏特征q/(mm/km) 1.3 近似正常高差精度估计 由式(3)、(4)可看出,影响O、P点近似正常高差精度的误差因素包括:大地高观测误差、基站和流动站仪器量高误差、RTK单点定位偏差对计算EGM2008模型高程异常值的影响和忽略实际高程异常短波部分差分值引起的误差。设mΔHop、mIop、mJop、mΔζopDM分别为上述相应的中误差,则O、P点的近似正常高差的精度的估算公式为: 1.3.1mΔHop估算 设RTK测量的基站点与流动点间距离为d(km),现代GNSS RTK仪器高程方向测量的标称精度均达到15 mm+1×10-6,则大地高差中误差的估算公式为: 1.3.2mIop估算 设基站点、流动点仪器高量测中误差分别为3 mm和1 mm,则仪器高量测中误差的估算公式为: 1.3.3mJop估算 设测区内的实际高程异常最大变化率为60 mm/ km,且RTK单点定位的平面误差为10 m[6],则RTK单点平面定位偏差对利用点位大地经纬度计算EGM2008模型高程异常差影响的中误差的估算公式为: 1.3.4mΔζopDM估算 由§1.2节的讨论可得出忽略实际高程异常短波部分差分值引起的误差的估算公式为: 设dcosa=s为作业等效距离,若取式(10)的极值误差作为其中误差即作业距离等于作业等效距离时,不影响对中误差的定性讨论,则忽略实际高程异常短波部分差分值引起的中误差的估算公式为: 将式(7)~(11)代入式(6)得出基站点与流动点间近似正常高差的精度估计公式为: 1.3.5m、q、d的关系分析 大比例尺(1∶500~1∶2 000)地形测量的等高距分别为0.5 m、1 m和2 m,相应的图根高程控制点中误差分别为5 cm、10 cm和20 cm,插求点高程中误差分别为16.7 cm、33.3 cm和66.7 cm[7]。若不考虑基站点已知高程误差,则流动点的高程中误差就等于基站点与流动点间的正常高差中误差,也就等于图根高程控制点或插求点的中误差;表2为由式(12)得出的m、q、d三者关系。从表2可以看出: 1)在高程测量限差m和测区地势类型q确定的情况下,表中d值为作业距离限制,表示可以在≤dkm范围内开展相应等高距的地形测量,利用EGM2008模型进行其RTK高程转换能满足规范[7]的要求。 2) 在m一定的情况下,q与d成反比,即q越大d越小,反之亦然。按规范[8]规定:d≤6 km,而表2中左下角未列出的d值均大于6 km,此时d值的应用要慎重。 表2m、q、d三者关系表 3)结合表1可知,①在海口市、临高县的平坦地区和陵水县的海滨平坦地区q≤20 mm/km,在d≤2.4 km范围内开展0.5 m等高距地形测量;在d≤4.9 km范围内开展1 m等高距地形测量;在d≤6 km范围内开展2 m 等高距地形测量时,利用EGM2008模型进行其RTK高程转换能满足规范[6]的要求。②在海口市、临高县台地地区和三亚市的海滨低丘地区一般20 2.1 概况 本文选择海口市、三亚市、临高县和陵水县中平原(q≤20 mm/km)、台地和低丘(20 表3 平原地区(q≤20 mm/km)流动点高程较差表 表4 台地和低丘地区(20 表5 丘陵和低山地区(30 2.2 实验结果分析 由表3~5可以看出: 1)在平原、台地和低丘、丘陵和低山地区,在相应的作业距离限制范围内开展相应等高距地形图根RTK测量的转换高程与已知点高程较差、较差均方差都满足相应大比例尺地形测量的高程精度要求。 2)虽然平均作业距离比作业距离限制大,但其平均等效距离比作业距离限制小,才能保证成果精度满足要求。若作业时无法确定作业等效距离,则要保证作业距离随时在作业距离限制范围内。 本文针对乏控测区,在保证成果精度的前提下,以EGM2008模型高程异常代替实际高程异常,推导出了大比例尺地形测量RTK高程转换的近似公式及其精度估计公式,即高程测量限差m、反映地势特征的实际高程异常短波部分的平均变化率q和作业距离限制d三者之间的关系式。研究结果表明,平原地区的作业距离限制宽松,分别达到≤2.4 km、≤4.9 km和≤6 km,有利于在这些乏控测区进行RTK大比例尺地形测量;台地和低丘地区的作业距离限制较宽松,分别为≤1.6 km、≤3.3 km和≤6 km,较有利于在这些乏控测区进行RTK大比例尺地形测量;而在丘陵和低山地区的作业距离限制较严格,分别为≤1 km、≤2 km和≤4 km,不利于在这些乏控测区进行RTK大比例尺地形测量。通过工程实验证明了在平均作业(等效)距离不超过本文推导的作业距离限制的前提下,在平原、台地和低丘及丘陵和低山地区开展RTK地形图跟测量的转换高程与已知点高程较差、较差均方差都满足大比例尺地形测量的高程精度要求。因此对于乏控测区,在各种地势条件且严格执行作业距离限制规定的前提下,大比例尺地形测量中直接利用EGM2008模型进行RTK高程转换,其结果精度能满足有关规范的要求,无需开展更多的耗时费力的水准或三角高程测量工作。由于实际高程异常短波部分起伏很不均匀,本次实验范围较小,上述结论有待于更大范围的验证。 [1] 余宣兴,詹昊,朱明新,等.EGM2008地球重力场模型在GPS高程转换中的应用研究[J].测绘通报,2013(12):18-20 [2] 张兴福,魏德宏,余旭,等.一种有效的GPS RTK高程测量方法[J].测绘通报,2012(1):3-6 [3] 姜元军,韩勇.EIGEN-6C重力场模型在中国地区的GPS/水准验证[J].测绘通报,2013(9):45-46,65 [4] 周始进,符永好,程真.风暴潮灾害评估的数据获取及整合方法研究[C]//海南省测绘学会.海南测绘地理信息局.成都:成都地图出版社,2011:11-16 [5] 倪明,文加林,丁仁军.基于EGM2008模型在GPS拟合高程中的应用[J].城市勘测,2014(4):99-100,108 [6] 高成发,陈安京,陈默,等.GPS精密单点定位精度测试与分析[J].中国惯性技术学报,2006,14(6):23-26 [7] 中华人民共和国建设部.CJJ/T 8—2011城市测量规范[S].北京:中国建筑工业出版社,2012:52-60 [8] 中华人民共和国住房和城乡建设部.CJJ/T 73—2010卫星定位城市测量技术规范[S].北京:中国建筑工业出版社, 2010:34-45 图4 未进行特性线优化构建TIN及生成的等高线效果 图5 进行特性线优化后构建TIN及生成的等高线效果 本文通过合理设置TIN的边界值,对TIN边界和特性线规则优化进行了探讨。实际生产表明,基于该方法构建生成的DEM和等高线能够比较准确地反映实际地形特征,同时节约了后期等高线修绘时间,提高了工作效率;但整个过程仍存在过多的人工干预,需进一步改进和完善。 参考文献 [1] 孙振勇.2015金沙江下游梯级水电站水文泥沙观测技术总结[R].重庆:长江委上游水文局,2015:1-2 [2] 李志林,朱庆.数字高程模型[M].武汉:武汉测绘科技大学出版社,2000:34-59 [3] SL 58-2014.水文测量规范[S]. [4] 魏猛,冯传勇,罗兴.清华山维在地形图等高线自动生成中的应用[J].长江工程职业技术学院学报,2014,31(4):1-2,9 [5] 贾俊涛, 翟京生,谭冀川.海底地形数据的格网DEM内插方法[J].海洋测绘,2003,23(6):24-26 [6] 李梅,张学雷.不规则三角网生成算法及其应用探讨[J].测绘与空间地理信息,2010,33(2):44-45,48 [7] 清华山维有限公司.EPS脚本语言帮助[Z].北京:清华山维有限公司,2007:28-29 [8] 茆德柱.TIN模型的构建方法研究[D].南京:河海大学,2007:19-22 第一作者简介: 任勇,工程师,从事水文测验、河道勘测等工作。 P22 :B :1672-4623(2016)11-0103-04 10.3969/j.issn.1672-4623.2016.11.035 符阳,主要从事工程测量、土地测绘工作。 2016-08-11。




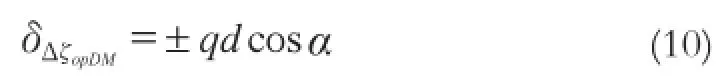


2 实验介绍与结果分析



3 结 语


4 结 语

