基于RS的淮河流域土壤含水量估算方法

陈立文，陈 晨，唐晓玲，陈 曦，刘明奇

（1.吉林省气象科学研究所，吉林 长春130062；2.江苏省地质调查研究院，江苏 南京 410000；3.吉林市气象局，吉林 吉林 132011；4. 吉林省气象服务中心，吉林 长春 130062）

基于RS的淮河流域土壤含水量估算方法

陈立文1，陈 晨2，唐晓玲1，陈 曦3，刘明奇4

（1.吉林省气象科学研究所，吉林 长春130062；2.江苏省地质调查研究院，江苏 南京 410000；3.吉林市气象局，吉林 吉林 132011；4. 吉林省气象服务中心，吉林 长春 130062）

运用MODIS等数据，建立了基于能量平衡与水量平衡的地表土壤含水量遥感反演模型。模型验证结果表明，山东半岛地区实测值与模拟值相关性R2为0.63，沂沭泗流域R2为0.6，淮河地区R2为0.65，适合研究区域不同季节不同分区土壤含水量预测。对将RS用于土壤含水量估算有一定参考价值。

土壤含水量；LST/NDVI斜率；降雨量；土壤质地；蒸发

合理准确地估算土壤含水量具有重要意义，因而受到水文、气象、农业、土壤、生态等多个学科的关注。RS能够快速方便地获取大区域地表信息，因此使用RS监测土壤水分意义重大。以LST/NDVI特征空间以及LST/NDVI斜率为参数能够定量反演土壤含水量，Hope A S[1]等研究发现，LST/NDVI直线斜率与土壤湿度状况有关；Nemani R R[2]等研究认为在同一幅图像上，提取不同地点（如13×13窗口）的LST/NDVI斜率，可反映各地土壤湿度状况；Goetz S J[3]认为LST/NDVI斜率的变化还可以反映地区土壤湿度的时间变化和年际土壤湿度变化。柳钦火[4]等通过分析14 a全国NOAA的8 km合成数据集发现，在LST/NDVI特征空间中，曲线斜率与实测土壤湿度显著相关，并利用9像元×9 像元窗口提取的LST/NDVI干边斜率反演了1981～1994 年全国土壤含水量分布；辛景峰[5]等利用NOAA数据，研究了土壤湿度与地表温度/植被指数斜率的定量关系；姚春生[6]利用1 km分辨率的MODIS数据，49 像元×49像元窗口提取的LST/NDVI干边斜率反演了全国2003年8～10月土壤含水量。本文旨在应用RS/GIS技术，综合利用大量多源、多尺度、多时相卫星遥感影像数据、降水数据、地面气象站观测数据以及土壤质地数据，探索建立具有一定物理意义的基于能量平衡与水量平衡的适合淮河流域土壤表层含水量计算的模型，为气候变化下淮河流域水文响应循环研究提供技术支持。

1 研究区域与数据来源

1.1 研究区概况

淮河流域（图1）地处我国东部，介于长江和黄河两流域之间，面积为27万km2。淮河平原属半干旱、半湿润地区，主要作物有小麦、水稻、玉米、薯类、大豆、棉花和油菜等；年降水量为500～900 mm，季节分配不均，集中在夏季，7～8月的降水量约占全年的45%～65%，秋、冬、春3季均为水分亏缺的干旱期。水对粮食作物的生长和生产至关重要，因此对淮河流域土壤含水量的研究有助于促进粮食产业的发展，对全国的经济发展都有一定的贡献。

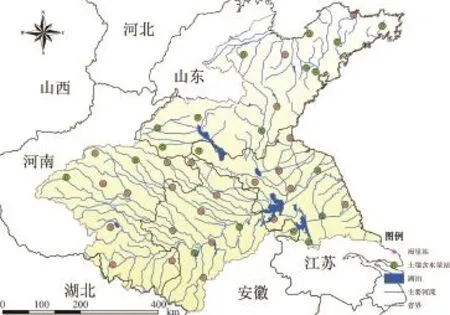
图1 研究区概况（审图号：GS（2014）6032）

1.2 研究资料数据

淮河流域土壤含水量时空变化监测过程中，涉及到大量多源、多尺度、多时相卫星遥感影像数据、基础地理数据、气象数据、土壤湿度数据、土壤质地类型数据以及DEM数据等。所有影像数据均重采样成空间分辨率为1 km，并统一到同一投影信息中，主要数据集及说明如表1所示。

本文选择2010年生长季（3～11月）的MODIS产品数据作为主要信息源，分别为16 d合成的1 km分辨率的MOD13A2植被指数产品数据和8 d合成的1 km分辨率的MOD11A2地表温度产品数据。对上述数据进行几何校正、投影变换，为了防止水体对特征空间造成影响，对NDVI数据水体进行了掩膜处理。

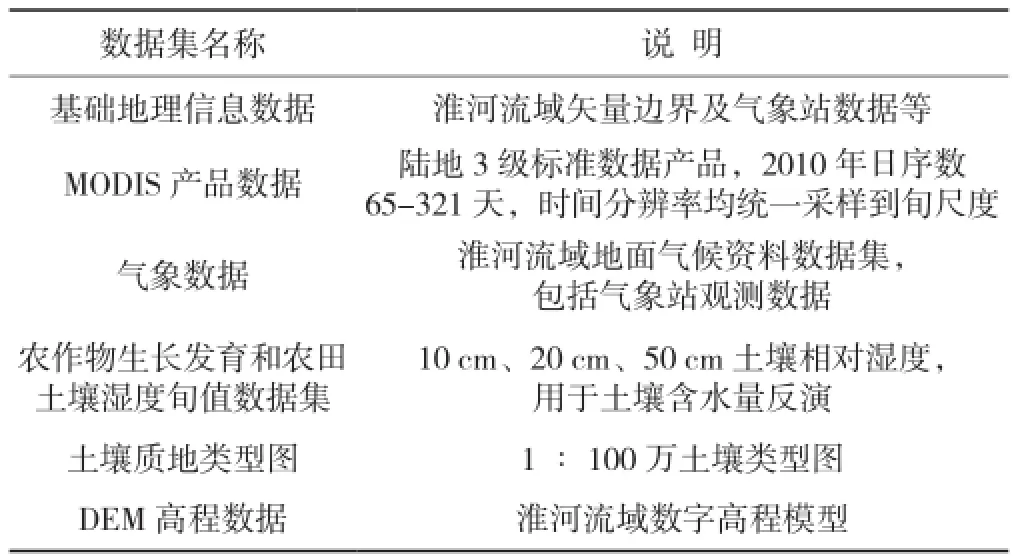
表1 淮河流域资料数据集

1.3 研究区分区

按照2010年淮河流域水资源公报中对各水资源分区的定义，以DEM为数据源，对其进行填洼，河网提取，得到各个集水区域。淮河流域共包括5个水资源分区，分别为淮河上游、淮河中游、淮河下游、沂沭泗流域以及山东半岛。进一步考虑淮河流域气象站和水文站分布情况，以及地形地貌特征、水热条件及地表覆盖分布特征，将淮河流域上、中、下游合并成一个区域，整个研究区分为山东半岛、沂沭泗流域、淮河地区3 个研究区，各分区的面积及位置说明如表2所示。

表2 淮河流域各分区统计信息

2 研究方法

2.1 LST/NDVI 斜率参数提取

在土地覆盖类型主要为植被的研究区域，由植被指数和温度所构成的散点图将呈现为梯形。图2中LST/NDVI特征空间点A表示土壤干旱的裸地（植被指数低，温度高），而B表示土壤湿润的裸地（植被指数低，温度低）。基于能量平衡，植被多的地方温度会低，D表示干旱的密闭植被冠层（植被指数高，温度高），土壤湿度低，导致植被蒸腾弱；C表示湿润的密闭植被冠层（植被指数高，温度低），土壤湿度高，导致植被蒸腾强。AD表示LST/NDVI 特征空间的干边，土壤湿度低的状态；BC表示LST/NDVI 特征空间的湿边，土壤湿度高的状态。假如在一个植被覆盖低的小区域遥感影像中，由于植被少，研究区小，温度差异就不大；而某一时刻该区域的影像，其温度植被指数所构成的散点图为三角形，则表明该研究区的干边和湿边条件不是很明显[7]。

图2 植被指数与地表温度特征空间

在LST/NDVI特征空间中，干边斜率与实测土壤湿度显著相关[4]。干湿边拟合的常数项表示的物理意义是当土壤水分低和高时的地表温度[8]。前人发现蒸散、土壤含水量等因子可导致干湿边斜率的变化[9]；干湿边斜率随时间的变化较为随机，没有明显规律，因斜率受上述3种因素的影响较大；但干湿边的变化规律较为一致[9]，干湿边斜率同时相应增大或减小。LST/ NDVI 特征空间在某些时段拟合精度较低的原因主要是MODIS产品计算可能存在误差，从而影响线性拟合的精度。姚春生[6]使用LST/NDVI特征空间斜率法对全国土壤含水量进行反演，从而得出LST/NDVI特征空间斜率法不仅能对土壤绝对含水量进行反演，而且能对全国土壤湿度的时空变化进行分析的结论。基于以上原因，本文在模拟土壤含水量反演模型中考虑了LST/NDVI斜率因子。在提取斜率时，根据在黄河源区土壤含水量反演中得出的结论，对于MODIS遥感影像1 km分辨率的适宜尺度为提取土壤含水量观测站附近9像元×9像元窗口的干边斜率[10]。再考虑到不同时期、不同地点植被指数范围可能存在差异，故在利用ENVI/IDL二次开发语言提取斜率时，目视判读散点主要集中在所在区域，以保证所选斜率的适宜性及精确性。

2.2 旬平均降雨统计与插值

降水是水量平衡中的重要参数，也是土壤水分的重要来源。当降雨量较多时，地表供水充分，土壤含水量高。降水落到农田，首先迅速增大表层土壤含水量，同时向下入渗。当表层土壤含水量达到田间持水量后，形成的重力水便迅速向下入渗补给地下水。在雨后的一定时段，土壤水接近饱和，并由于充分供水，这时的蒸散发强度很大，土壤水消退较快；随着降雨停止，表层土壤水逐渐减少，蒸散发向下层土壤延伸，强度也逐渐减弱[11]。所以在模拟土壤含水量反演模型时考虑降水量是有必要的。

降水量数据来自中国气象数据共享服务网中日值数据，按淮河地区降水量观测站下载的数据。由于下载的数据为点数据，为了满足计算需要，要将数据从点到面进行转化，本文利用Kriging插值将降雨量点数据插值到面。研究中土壤水数据时间尺度为旬，而降水量数据为日数据，需要将降水数据与土壤含水量数据进行时间尺度匹配。降雨量数据为研究区内降雨站点数据求取每10 d数据的平均值，经过Kriging插值所得到旬数据。

2.3 饱和导水率与田间持水量数据计算

相同吸力条件下，土壤水分农田最大、林地最小，而饱和导水率则相反；除土壤水分消耗期的林地和苜蓿地土壤水分随土层深度增加呈上升趋势外，其他时期各土地利用方式下土壤水分均随土层深度的增加而降低。土壤剖面饱和导水率与土壤含水量之间的影响程度依土壤水分条件而异[12]。哥伦比亚土壤学教授Kumar等研究了农林缓冲带、草地缓冲带、轮作草地及连续放牧草地的饱和导水率、持水力，以评价草地缓冲带和农林缓冲带对土壤水分特性的影响[13]。本文在研究土壤含水量时主要考虑了土壤饱和导水率及田间持水量两个因子（图3）。

图3 淮河流域土壤饱和导水率与田间持水量（审图号：GS（2014）6032）

2.4 潜在蒸发数据提取

土壤湿度直接作用于植被的呼吸、蒸腾和各种化学反应，是生态气象学的重要环境因素。蒸发对土壤湿度具有持续的耗散作用，可视为连续的。为阐释蒸发对土壤湿度的影响，本文在建立土壤含水量反演模型时将蒸发考虑为土壤水分消减的因子，通过土壤湿度响应模型对其进行定性分析[14]。孙福宝[15]等在基于Budyko假设的黄河流域水热耦合平衡规律研究中，提出将多年平均的年潜在蒸发量无量纲化，即可得到相对植被土壤蓄水能力。本文在研究土壤含水量平衡规律时考虑了研究区内潜在蒸发对土壤含水量的影响。

3 土壤含水量模型的建立

目前，对于淮河流域土壤含水量与模型的定量化研究较少，并且现有成果大多未考虑研究区域地形地貌特征、土壤自身性质、降水、蒸发等条件。针对以上问题，本文分析了淮河地区2010年春季气象因子、LST/NDVI斜率、土壤质地序列数据集对土壤含水量的驱动影响，利用2010年6月、7月、10月影像数据对模型进行验证分析。

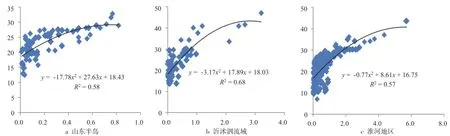
图4 土壤含水量与相对持水能力相关关系图

3.1 土壤含水量与驱动因子相关性分析

3.1.1 土壤相对持水能力分析

根据能量平衡原理，在建立土壤含水量模拟模型时要考虑土壤的持水能力以及土壤含水量消耗能力。除了气候条件，地形地貌、土壤和植被等下垫面特征是影响流域水量平衡的主要因子。根据孙大福等提出的土壤饱和导水率控制着降水入渗从而影响土壤供水的理论[15]，本文利用旬平均降水与饱和导水率之比得出土壤相对持水能力。

如图4所示，横轴为土壤相对持水能力，纵轴为土壤含水量实测值，土壤含水量与相对持水能力的相关系数R2在山东半岛、沂沭泗流域、淮河地区分别为0.58、0.68和0.57。

3.1.2 土壤含水量相对消耗能力分析

利用LST/NDVI特征空间干边斜率反演土壤含水量研究发现，土壤含水量实测站点附近某一尺度像元窗口LST/NDVI特征空间干边斜率与土壤含水量呈正相关关系。当LST/NDVI干边斜率接近0时，根据温度植被指数所构成的LST/NDVI特征空间，当植被指数一定时温度越高说明土壤含水量越高。由于土壤含水量应随着潜在蒸发的增大而减小，随LST/NDVI干边斜率的增大而增大，所以本文利用土壤含水量与LST/NDVI特征空间斜率以及潜在蒸散发进行相关性分析并建立相互关系，研究发现土壤含水量与LST/ NDVI特征空间斜率和潜在蒸散发的乘积成负相关关系。

如图5所示，图中横轴为LST/NDVI特征空间斜率和潜在蒸散发的乘积，纵轴为土壤含水量实测值，土壤含水量随着LST/NDVI特征空间斜率和潜在蒸散发的乘积的增大而减小，且减小速度逐渐减缓。LST/ NDVI干边斜率为负值，LST/NDVI特征空间斜率与潜在蒸散发乘积为负，随着蒸散发的减小而增大；而当乘积大于某一值时，说明潜在蒸散发减小到对土壤含水量的敏感性小于LST/NDVI干边斜率对土壤含水量的影响，所以土壤含水量会随着乘积增大而减小，且减小速度逐渐下降，类似于加速度减小的加速运动；而当潜在蒸散发小到一定程度时，斜率的增大对土壤含水量的敏感性逐渐大于潜在蒸散发，所以土壤含水量到后来的变化逐渐趋于平缓。研究区内的山东半岛、沂沭泗流域和淮河地区，当LST/NDVI特征空间斜率以及潜在蒸散发乘积约为-60时土壤含水量下降速度趋于平缓。

图5 土壤含水量与相对消耗能力相关关系图

将LST/NDVI特征空间斜率与潜在蒸散发的乘积定义为土壤含水量相对消耗能力，由图5可见，土壤含水量与土壤含水量相对消耗能力的相关系数R2在山东半岛、沂沭泗流域、淮河地区分别为0.69、0.62和0.58。

3.2 研究区土壤含水量模拟模型建立

土壤含水量在空间上的变化是温度、降水以及其他气象要素和下垫面覆盖类型相互作用的结果。NDVI对植被的生长势和生长量非常敏感，可以很好地反映地表植被的繁茂程度，在一定程度上能反映下垫面植被覆盖情况，而地表温度又直接影响到土壤的蒸发，所以有些研究直接利用NDVI与LST计算的TVDI反映土壤湿度情况，但TVDI只能定性的说明土壤的干旱、湿润，不能定量地反映土壤含水量。而研究认为LST/ NDVI特征空间干边斜率与土壤含水量有密切关系，为了定量描述下垫面情况对土壤含水量的影响，特引用LST/NDVI斜率因子进行研究。因而，可将影响土壤含水量的5个主导因子：土壤饱和导水率、降水、潜在蒸散发、田间持水量以及LST/NDVI斜率参数，抽象成一个空间和时间上的定量模型，表达式为：

式中，Js为单位时间降水；E为潜在蒸散发；Ln为LST/NDVI特征空间斜率（无量纲）；W为土壤含水量，代表一种基于空间上气象因子以及土壤因子对土壤含水量影响的定量化函数关系。本文选取2010年春季序列数据集，以土壤含水量为因变量，气温、NDVI、降水、土壤饱和导水率，潜在蒸散发因素为自变量，结合遗传规划算法，通过判定各拟合函数的适应度，进行多次迭代，建立适合淮河流域各分区土壤含水量的估测模型。

由于研究区内下垫面复杂，为避免山地及平原地区土壤水模拟时相互影响，从而导致平原地区模拟值偏低及山地地区模拟值偏高，将研究区分为山东半岛、沂沭泗流域、淮河地区3个地区。以山东半岛、沂沭泗流域、淮河地区模型建立为例，建立土壤含水量模拟模型。

经多次实验，得到拟合公式分别为：山东半岛W=23.977(Js/Sk)0.075(E×Ln)0.216，其相关系数R2为0.6；沂沭泗流域W=32.212(Js/Sk)0.143(E×Ln)0.081，其相关系数R2为0.6；淮河地区W=27.943(Js/Sk)0.157(E×Ln)0.151，其相关系数R2为0.59。

4 结 语

由于缺少研究区内土壤含水量实测值验证数据，为了验证所建立模型的可靠性，选用2010年6月上、中、下旬，9月下旬，10月中旬实测数据与淮河流域各分区模型模拟的土壤含水量值进行对比验证。研究结果为山东半岛、沂沭泗流域、淮河地区的模拟值与实测相关性R2分别为0.63、0.60、0.65，均方根误差分别为0.09 、0.12、0.11。

由图6可知，3个分区实测值与模拟值斜率与45°线相差不多，截距在0.1左右，说明估测值比实际值偏小。在山东半岛，当土壤相对含水量小于0.8时，模拟值略高于实测值；当大于0.8时，模拟值偏小。淮河地区有相似情况，临界值出现在0.6左右，在0.6～0.8之间出现一些站点的模拟值高于实测值0.3左右的异常情况。在沂沭泗流域，模拟值整体高于实测值。在相关性分析的基础上，进一步作相互独立的两组样本的显著性分析，山东半岛、沂沭泗流域、淮河地区均通过检验（a=0.01）。

图6 土壤含水实测值与模拟值相关性分析

利用研究区内山东半岛、沂沭泗流域、淮河地区6月上、中、下旬，9月下旬，10月中旬土壤相对含水量实测数据，与所建立模型估算所得土壤相对含水量模拟数据进行误差分析，如图7。其中山东半岛有8个站点数据，沂沭泗流域有8个站点数据，淮河地区有18个站点数据。

图7中横坐标为研究区3个分区土壤水分实测站点，纵坐标为各实测站点实测数据与估测数据误差百分比，可以看出，山东半岛整体误差低于沂沭泗流域与淮河地区，山东半岛除了在6月上旬和第2个站点高于20%外，其余均控制在15%之内；沂沭泗流域，整体误差高于山东半岛，最高误差为25%；淮河地区由于站点较多，误差高于15%的较多，但按比例分析高于15%占整体的8.9%，低于沂沭泗流域；研究区3 个分区整体满足误差要求。这说明得到的定量关系式符合客观规律，能够满足研究需要。误差估测大小与土地覆盖类型等下垫面因子以及气象因子有关，如在沂沭泗流域，由于山地、裸地较多，降雨可能入渗较少，所以降雨对土壤含水量影响没有平原地区大。由此进一步验证了土壤含水量的大小受区域下垫面情况、气象条件等因子影响和控制的结论。

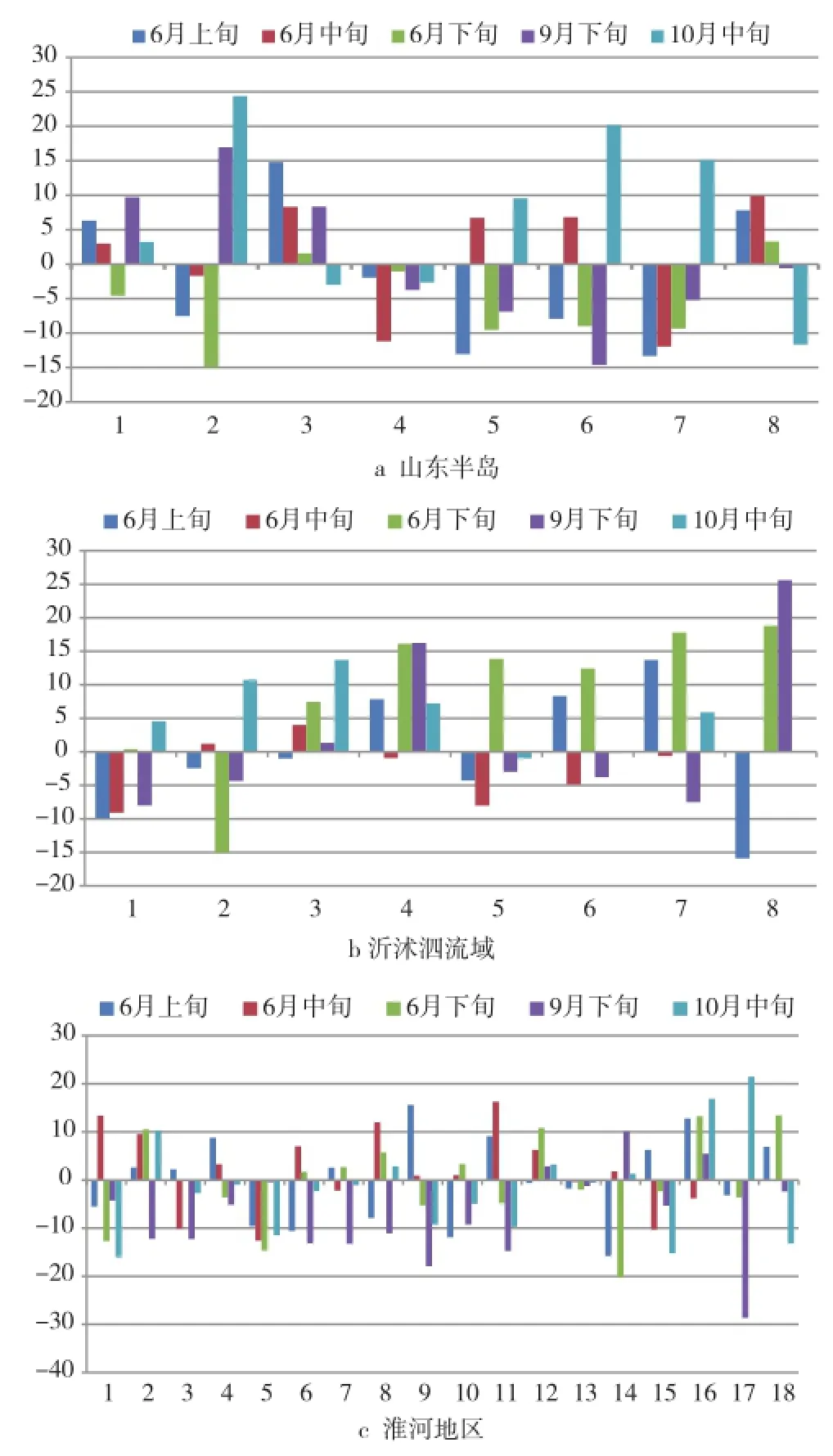
图7 研究区3个分区实测值与模拟值误差分析

该定量关系是基于区域尺度的，不仅考虑了温度、植被的影响， 同时加入了降雨、饱和导水率、潜在蒸散发等因子，还考虑了下垫面覆盖变化的影响，将RS与土壤质地数据结合，从而改进了传统土壤含水量估算模型中未考虑下垫面参数的不足。利用研究区土壤质地、气象数据集，基于遗传规划算法建立的蒸散发气象驱动模型，通过检验和误差分析，均通过a=0.01的显著性检验，适合研究区域不同季节不同分区土壤含水量的预测。

[1] Hope A S, Petzold D E, Goward S N, et al. Simulating Canopy Reflectance and Thermal Infrared Emissions for Estimating Evapotranspiration[J]. Water Resources Bulletin,1987,22(6)：1 011-1 019

[2] Nemani R R, Running S W. Estimation of Regional Surface Resistance to Evapotranspiration from NDVI and Thermal-IR AVHRR Data[J]. Journal of Applied Meteorology,1989,28(4)：276-284

[3] Goetz S J. Multi-sensor Analysis of NDVI, Surface Temperature and Biophysical Variables at a Mixed Grassland Site[J]. International Journal of Remote Sensing,1997,18(1)：71-94

[4] 柳钦火,辛景峰,辛晓洲,等. 基于地表温度和植被指数的农业干旱遥感监测方法[J].科技导报,2007,25(6)：12-18

[5] 辛景峰,宇振荣,Driessen P M.利用NOAA NDVI数据集监测冬小麦生育期的研究[J].遥感学报,2001(6)：442-447

[6] 姚春生.使用MODIS数据反演土壤水分研究[D].北京：中国科学院研究生院(遥感应用研究所),2003

[7] Carlson T N, Perry E M, Schmugge T J. Remote Estimation of Soil Moisture Availability and Fractional Vegetation Cover for Agricultural Fields[J].Agricultural and Forest Meteorology,1990,52(1)：45-69

[8] 杨曦,武建军,闫峰,等.基于地表温度—植被指数特征空间的区域土壤干湿状况[J].生态学报,2009(3)：1 205-1 216

[9] 李震,郭华东,施建成.综合主动和被动微波数据监测土壤水分变化[J].遥感学报,2002(6)：481-484

[10] 陈立文,张友静,邓世赞,等.基于温度植被干旱指数的黄河源区土壤表层含水量反演[J].水利水电科技进展,2012,32(4)：6-9

[11] 季志恒,樊福来.土壤水消退的时空变化规律分析[J].水文, 2003(1)：23-27

[12] 刘春利,邵明安.黄土高原六道沟流域不同土地利用方式下土壤水力特性及其对土壤水分的影响[J].应用生态学报,2008,19(11)：2 400-2 407

[13] 赵术伟.放牧对缓冲带水分特性影响的研究[J].水土保持应用技术,2009(2)：17-19

[14] 刘春,张春辉,李秀梅.脉冲降雨—蒸发对土壤湿度影响的动力机制分析[J].高原山地气象研究,2011,31(2)：59-62

[15] 孙福宝,杨大文,刘志雨,等.基于Budyko假设的黄河流域水热耦合平衡规律研究[J].水利学报,2007(4)：409-416

[16] 傅抱璞.山地蒸发的计算[J].气象科学,1996(4)：328-335

P237

：B

：1672-4623（2016）11-0097-06

10.3969/j.issn.1672-4623.2016.11.034

陈立文，硕士，主要从事GIS与RS研究。

2015-07-03。

项目来源：吉林省科技发展计划资助项目（20140204052SF）。