规则波作用下透空格栅板式防波堤波浪力试验研究

程永舟，常佳夫，杨小桦，黄筱云，3

（1.长沙理工大学 水利工程学院，湖南 长沙 410004；2.长沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410004；3.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098）

规则波作用下透空格栅板式防波堤波浪力试验研究

程永舟1，2，常佳夫1，杨小桦1，黄筱云1，3

（1.长沙理工大学 水利工程学院，湖南 长沙 410004；2.长沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410004；3.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098）

透空格栅板式防波堤是一种新型防波堤结构，为了促进该结构在实际工程中的应用，论文通过模型试验研究其所受波浪点压力和波浪总力的特征。试验结果表明，在规则波作用下，下层水平格栅板所受波浪点压力较上层水平格栅板大，且防波堤中前端波浪点压力分布不规律；相对板宽B/L对该防波堤所受波浪总力的影响较大，相对板间距S/h对其整体稳定性的影响次之，而相对波高H/h主要影响该防波堤的垂向受力；此外，当上层水平格栅板与静水面齐平且孔隙率相对较大时，该防波堤所受波浪总力最小，对其整体稳定性最有利。

透空格栅板式防波堤；水平格栅板；波浪点压力；波浪总力；稳定性

随着深水港建设开发力度的加大，防波堤建设条件变得更加复杂。亟需研究和开发消浪效果好、工程造价低、环保且施工方便的新型防波堤结构。板式防波堤是一种新型防波堤结构，与重力式防波堤相比，板式防波堤具有较好的消浪效果，受力小，造价更加低廉，水体能够进行自由交换，利于海洋环境污染治理等众多优点。因此，许多学者对板式防波堤开展研究，它经历了从单层板，到开孔单层板，再到双层板甚至是多层板的发展过程。很多学者从板式防波堤的消浪效果出发，研究了其随相对水深，淹没深度，来波条件等参数变化下的消浪规律，但是从防波堤的局部稳定性和整体稳定性出发，对其的受力特性研究较少，因此也限制了板式防波堤在实际工程中的应用。

Patarapanich（1984）用势流理论的方法计算了由波浪绕射引起的实体薄板的波浪力和倾覆力矩，并与有限元方法所得结论进行了对比，发现该薄板式防波堤所受垂直力和倾覆力矩均随淹没深度和相对水深的增加而减少。Rey等（2011）在Patarapanich（1984）的研究基础上进一步研究了不同来流条件时该板式防波堤所受的水动力荷载和力矩，为该淹没板式防波堤在实际工程中的应用奠定了基础。邱大洪等（1986）首次将板式防波堤引入国内。王科等（2011）研究了平板及立板式防波堤在3个自由度上所受的垂荡、横荡和横摇波浪力。虽然单层实体薄板具有工艺简单便于安装等一定的优势，但是当波浪传播至防波堤前沿时，波高增加会导致板式防波堤前端迎浪面的波压力急剧增大，由于受力不均，会导致防波堤倾斜或造成局部破坏，对防波堤的安全和稳定性造成不利影响。因此在单层实体板式防波堤的基础上，Chwang等（1983）首先提出了单层开孔板式防波堤，Yip等（2000）用势函数理论分析了前端为竖直开孔板，中间为内置水平实体板，后方为竖直实体板的板式防波堤的孔隙参数，力系数，力矩系数等参数对防波堤消浪和受力的影响，并发现合适的孔隙率能最大限度的消减波能从而提高该防波堤的稳定性。Wu等（2002）又用类似的方法研究了圆形开孔板式防波堤，并指出，和实体板式防波堤相比，开孔的板式防波堤不仅能有效的减小入射波高，还能有效的减小作用在板式防波堤上的波浪荷载和倾覆力矩。

虽然单层板式防波堤有一定的优点和应用范围，但是在实际工程其很难达到满意效果。Cheong等（1992）首先提出了上层板与静水面齐平，下层板淹没的双层实体板式防波堤，并发现双层板式防波堤和单层板式防波堤比起来，波浪的反射系数更大，透射系数更小，更有利于防波堤的消浪；且能量损失系数即使在水深较大时也更大，即双层板式防波堤在水深较大的情况下应用前景更为广阔。Usha等（2005），Neelamania等（2006）再次验证了该结论。为增加双层板式防波堤的安全性，王志勇等（2012）等从其结构形式出发，探讨了不同支承形式、钢板厚度、H型钢加劲肋个数和型号等因素对水平板应力和变形的影响。为达到进一步消浪和减小防波堤受力等效果，Liu等（2008）提出了上层板开孔，下层板为实体板的双层板式防波堤模型，在分析其水动力特性和受力的基础上预言：若下层板也开孔，能进一步增加该模型的消浪特性和稳定性。Kweon等（2013）提出了3种不同的方法研究双层开孔板的受力特性，Kweon等（2014）在这基础上观测到了上水平板存在逆流现象，并探讨了上板逆流现象对波浪传播相位和防波堤受力的影响。王晶等（2015）对比了其提出的双层预制板装配式防波堤和双层开孔板式防波堤的受力情况，发现虽然前者受力只略小于后者，但其消浪特性要比后者更明显，因此，为该种双层预制板装配式防波堤在实际工程中的应用奠定了良好的基础。王国玉等（2005）则探讨了多层透空格栅板式防波堤的水动力特征。

本文提出的三层格栅板式防波堤结构是从双层预制板装配式防波堤（王晶等，2015）改进而来，着重分析了其点压力和波浪总力随相对板宽、相对板间距、相对波高的变化情况，为该板式防波堤在实际工程中的应用奠定基础，同时为板式防波堤的受力研究提供参考。

1 防波堤结构简介及试验布置

1.1防波堤结构简介

透空格栅板式防波堤由上、中、下3层格栅板组成，而每一层格栅板又由数个长条形水平预制板组成且开有一定孔隙，具体结构见图1。防波堤侧面与横梁相连，可调节长条形水平预制板之间的间距，背浪面用实体板封住，下部由4根桩基支撑。防波堤的主体消浪结构类似于一个组装的消浪室。

1.2试验布置

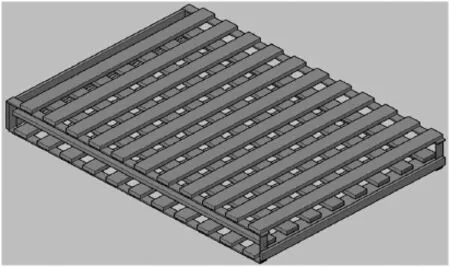
图1 透空格栅板式防波堤主体结构图

试验在长沙理工大学水利实验中心多功能波浪水槽中进行，水槽总长40 m、宽0.8 m、深1.0 m，最低工作水深0.3 m，最高工作水深0.8 m。水槽前端为推板式造波机，两侧为透明玻璃，末端设有直立式消能网，以消除波浪反射影响。造波控制系统采用大连理工大学海岸和近海工程国家重点实验室研究开发的Wave make系统，可产生单向规则波、不规则波，且产生的波形平稳，重复性好。试验整体布置图见图2。采用成都泰斯特电子信息有限责任公司研制高精度智能数字点压力传感器及其采集系统测量点压力，测量精度为0.1%，量程为0～ 20 kPa。在上、下层水平格栅板的上、下表面均对称布置各5个，各点压力传感器间距详见图3。采用扬州科动电子技术有限责任公司研制的二分量应变式测力天平测量总力，各分量测量范围-100 N～ 100 N，准确度：±0.5 N，线性度：＜1%。两个测力天平分别布置在防波堤下层板下表面中间的前后端，用以测量防波堤的整体受力情况，测力天平布置图详见图3。试验采用规则波，防波堤板宽B= 0.8 m，改变试验水深h、波长L、上、下水平格栅板间距S、防波堤淹没高度h’、水平格栅板孔隙率（上或下层格栅板孔隙面积之和与该层水平预制板面积之和的比值）G等参数。其中，中层各长条形水平预制板保持间距为2 cm不变。根据实际透空式防波堤的尺寸范围和重力相似准则，综合考虑水槽尺寸、造波机和试验采集仪器的精度等影响因素，本模型比尺采用1∶25。

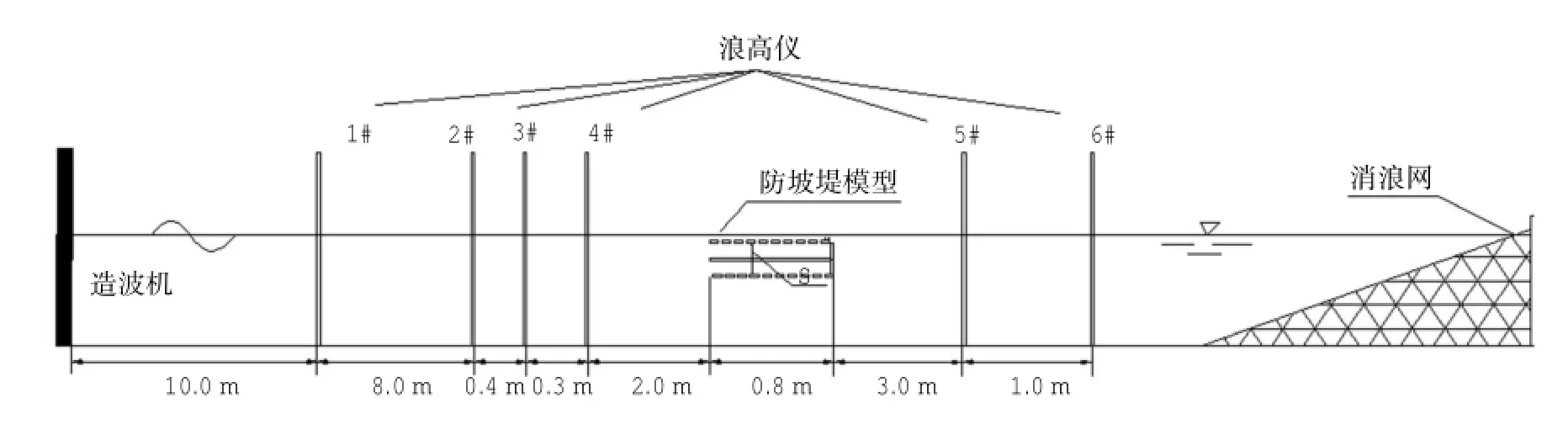
图2 试验整体布置图

图3 试验点压力传感器及测力天平布置图

波浪点压力测量试验组次见表1，波浪总力测量试验组次见表2。试验规定：当防波堤上层格栅板与静水面齐平，即h′=0 m时，称之为平水堤；当防波堤上层格栅板位于静水面以下，即h′= -0.05 m时，称之为淹没堤；同理有出水堤，即h′= 0.05 m，上层格栅板位于静水面以上。为消除试验的随机性，对同一次试验组次进行三次测量，每一次取波浪传播稳定后8个波浪周期受力的平均值；待水面平静后，进行下一组次试验的测量；且在每个波况结束后，检查防波堤的稳定状况及各试验仪器的连接情况。若出现异常，则重新测量该组次试验。

表1 波浪点压力试验组次

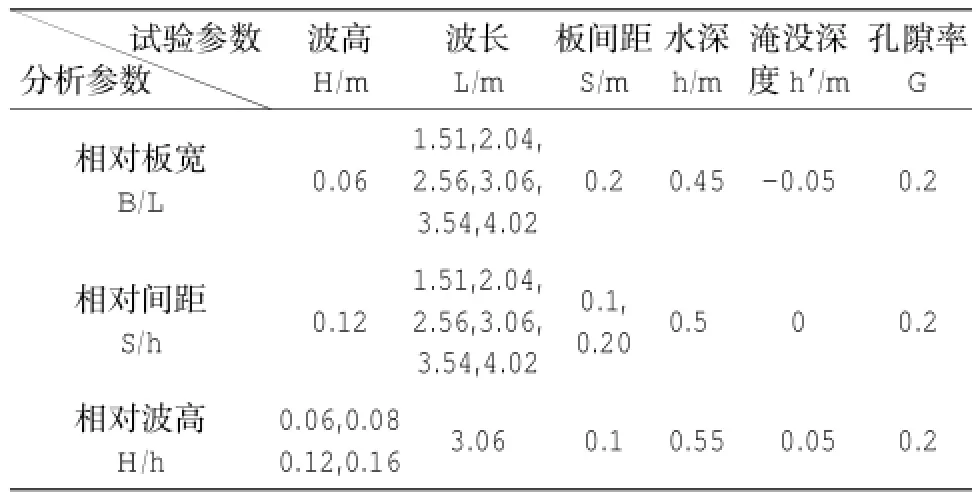
表2 波浪总力试验组次

2 压力分析方法

2.1点压力分析方法

为研究防波堤所受波浪点压力，参考Kweon等（2013）、Kweon等（2014）提出的对双层水平板式防波堤局部点压力的处理方法，以透空格栅板式防波堤的上、下层水平格栅板为研究对象，且以同一层板上下对称布置的压力传感器所测点压力之和作为该板所受的波浪点压力。其中，1#-5#及6#-10#点压力传感器分别布置在上、下层水平格栅板下部；11#-15#及16#-20#点压力传感器分别布置在上、下层水平格栅板上部，详见图3。计算公式为：

2.2总力分析方法

为研究防波堤所受波浪总力，参考Yu等（1994），Liu等（2008）等提出的力系数CF概念，对透空格栅板式防波堤所受波浪总力进行无量纲化处理。其中，

可反应防波堤所受波浪总力大小。

3 试验结果分析

3.1相对板宽B/L对透空格栅板式防波堤点压力和总力的影响

图4描绘了透空格栅板式防波堤的上层（图4（a））、下层（图4（b））水平格栅板点压力分布随相对板宽B/L的变化情况，其中，纵坐标P/ρgH为无量纲化点压力。从图4可看出，上层水平格栅板的点压力分布基本随相对板宽B/L的增加而增大，且当B/L超过0.3时，变化幅值增大明显。而下层水平格栅板则刚好相反，其点压力分布基本随相对板宽B/L的增加而减小，且当相对板宽B/L小于0.3时，其变化幅值增大明显。综合考虑上、下层水平格栅板点压力分布规律可得：当B/L位于0.3附近时，上、下层水平格栅板所受点压力均相对较小，对实际工程中防波堤的局部稳定性有利。Yip等（2000）在研究由单层开孔板和实体板组成的消浪室时也指出，当消浪室的长度与入射波波长的比值介于20%～25%时，为消浪室的最佳尺寸。

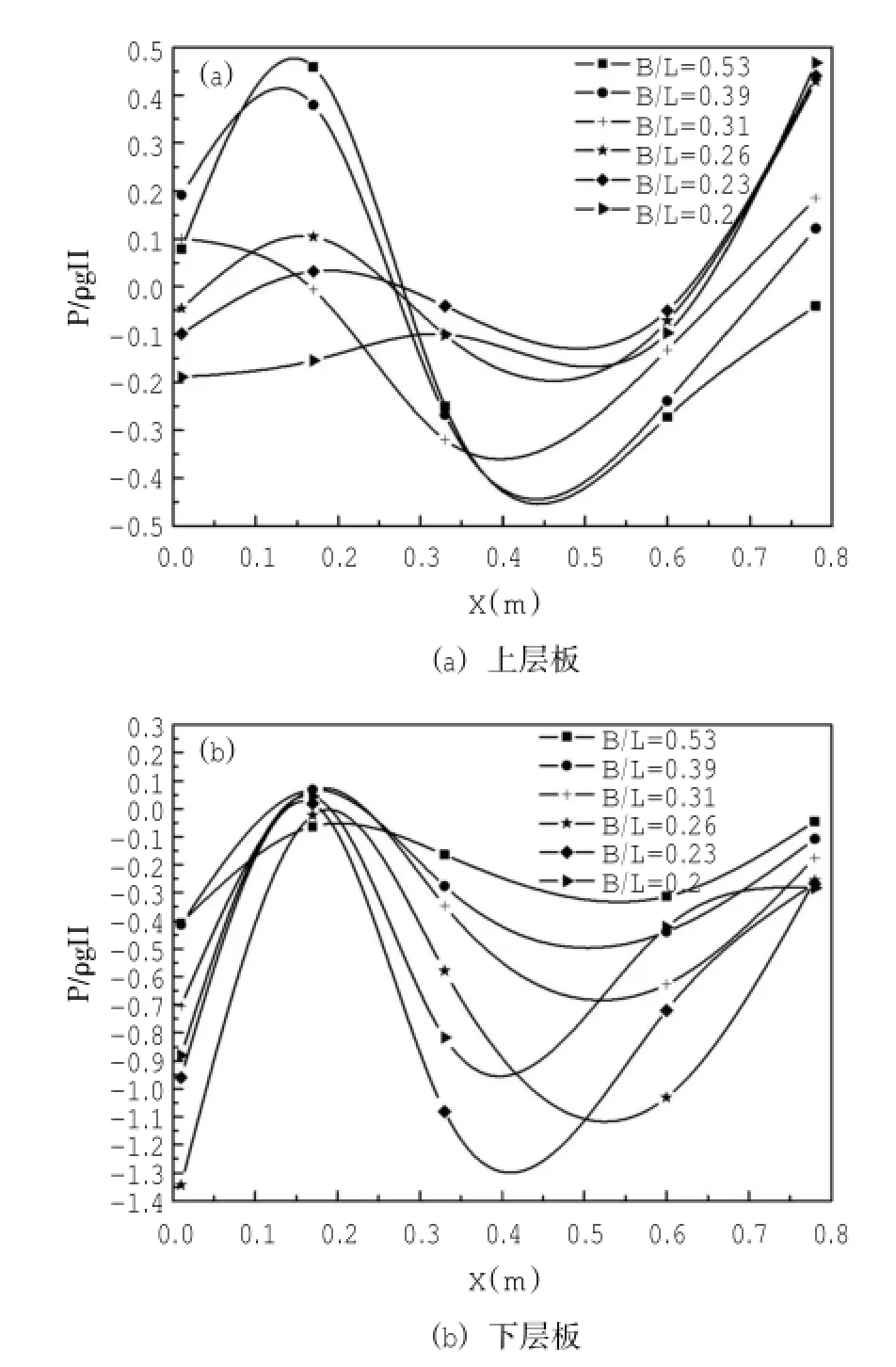
图4 防波堤上层、下层板点压力分布随相对板宽B/L的变化情况

此外，从图4可发现在防波堤的中前端，即当X/B=0.2～0.4时（B为防波堤板宽，B=0.8 m），防波堤的上、下层水平格栅板点压力分布不规律。这是因为当波浪传播至防波堤前端时，波高增加变陡，波浪在防波堤中前端引起的震荡达到最大值，入射波和反射波的相互作用最强烈，因此，在防波堤的中前端，点压力随B/L的变化不明显；而随着波浪逐步传播至防波堤后端，上、下层水平格栅板点压力随B/L的变化则越规律。

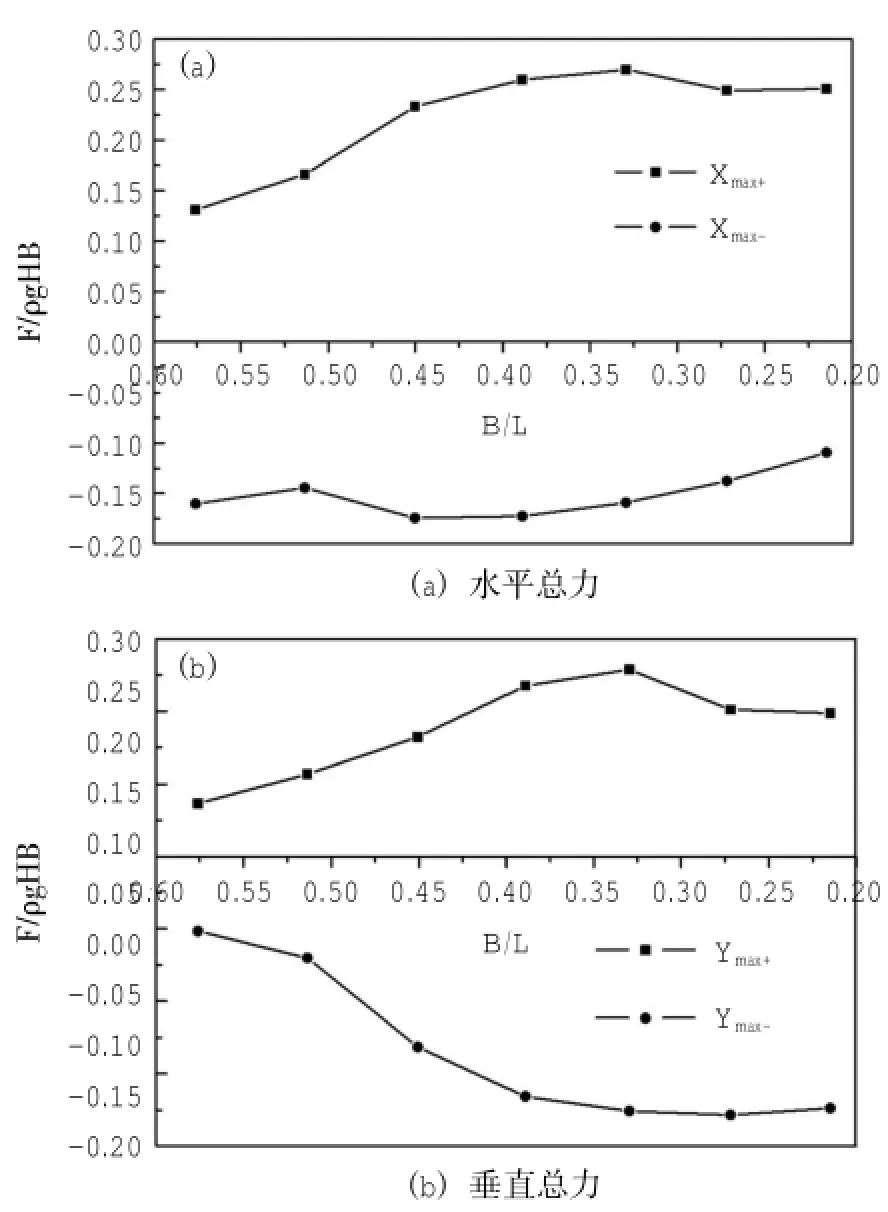
图5 防波堤所受波浪总力随相对板宽B/L的变化情况

图5给出了当防波堤为出水堤，水平格栅板孔隙率G=0.2时防波堤所受无量纲（即力系数CF）波浪水平总力（图5（a））和垂直总力（图5（b））随相对板宽B/L的变化情况。其中，Xmax+、Ymax+分别表示水平和垂直正方向防波堤所受波浪总力的最大值，同理有Xmin-、Ymin-（图7、图9同理）。从图中可知，防波堤所受水平和垂直总力均基本随相对板宽B/L的减小而增大，且在B/L=0.3左右达到稳定。这是因为随着相对板宽B/L的减小，波长相对较长时能更容易到达防波堤后方的竖直挡板处，所以，当相对板宽B/L较小时防波堤所受波浪总力相对较大。

此外，从图5可知，防波堤所受正方向的波浪水平总力略大于负方向的波浪水平总力，而所受正方向的垂直波浪总力略小于负方向的垂直波浪总力，由力的合成定理可知，防波堤可能会受到向后倾斜的合力，因此在实际工程中，应考虑该透空格栅板式防波堤的倾覆力矩。

3.2相对板间距S/h对透空格栅板式防波堤点压力和总力的影响

图6描绘了透空格栅板式防波堤的上层（图6（a））、下层（图6（b））水平格栅板波浪点压力分布随相对板间距S/h为0.2、0.3、0.4时的变化情况。从图6中可以看出防波堤的上、下层水平格栅板均以受到向下的波浪点压力为主。其中，上层水平格栅板所受波浪点压力基本以防波堤上层板中点为对称分布（即若以防波堤宽度的中点X=0.4建立坐标轴；下同），但是在防波堤末端波浪点压力值有上扬（S/h=0.3）或下倾（S/h=0.4）的趋势，即随着相对板间距S/h的增加，上层水平格栅板所受波浪点压力的振荡特征表现得越明显；而下层水平格栅板则在相对板间距S/h=0.3时所受波浪点压力最小且相对对称。综合上、下层水平格栅板所受波浪点压力分布随相对板间距S/h的变化情况可得出：当相对板间距S/h不超过0.3时，防波堤所受波浪点压力的分布较对称，波浪点压力值也较小，有利于防波堤的局部稳定性。

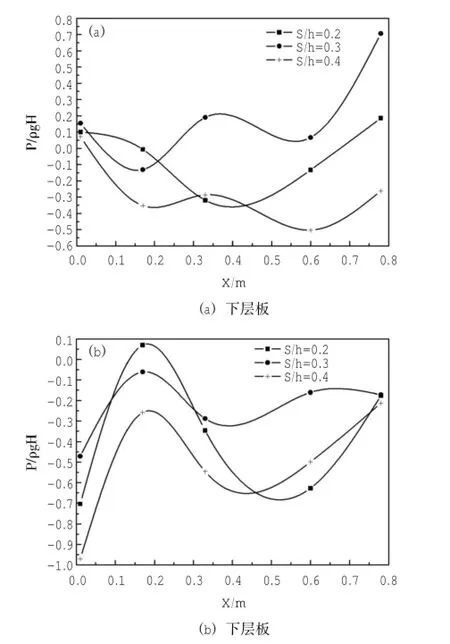
图6 防波堤上、下层板点压力分布随相对板间距S/h的变化情况

另外，通过对比图4（b），图6（b），图8（b）中下层水平格栅板所受波浪点压力分布情况，可以发现一个试验规律：即使研究的参数B/L，S/ h，H/h不同，透空格栅板式防波堤的下层水平格栅板所受波浪点压力均在同一量级，且分布规律均比较类似，Rey等（2011）在研究单层时也得出了同样的结论。即波浪点压力变化曲线均类似于起点在Y轴负方向，幅值不断减小，最后聚于零点的余弦曲线。这是因为当波浪传播至透空格栅板式防波堤里面时，由于上、中、下3层水平格栅板均有一定的孔隙率，而防波堤后方有竖直挡板，相当于波浪进入消浪室，由此使得水质点在消浪室中的运动更加复杂，波浪一定经历了一个复杂的转变过程，而这个转变过程，始终伴随着波浪的折射、透射、反射、以及能量的损失和相位差（Liu et al，2007；Wu et al，2002），因此，防波堤下板所受波浪点压力随着波浪在消浪室中的运动而逐步减小且基本最后归于零。在实际工程中，为保证防波堤的安全性，防止下层水平格栅板因受压破坏，建议在下层水平格栅板的中前端进行局部加固处理。

图7给出了透空格栅板式防波堤所受波浪水平总力（图7（a））和垂直总力（图7（b））随相对板间距S/h的变化情况。从图中可以看出，相对板间距S/h对防波堤所受波浪水平总力影响较大，当相对板间距S/h增加时，波浪水平总力正负方向均迅速增大；而相对板间距S/h对防波堤所受波浪垂直总力影响较小，当相对板间距S/h增加时，波浪垂直总力正负方向增值幅度相对较小，因此，当相对板间距S/h相对较小时，更有利于防波堤的整体稳定性。

对比图5，图7，可知相对板宽B/L对透空格栅板式防波堤所受波浪水平和垂直总力较相对板间距S/h时大得多，从总力的竖坐标可以看出二者根本不在同一数量级。因此可知，从防波堤的结构对其受力而言，相对板宽B/L较相对板间距S/h影响大得多。

图7 防波堤所受波浪总力随相对板间距S/h的变化情况

3.3相对波高H/h对透空格栅板式防波堤点压力和总力的影响

图8给出了波长L=2.56 m，相对板宽B/L= 0.31（其中B=0.8）时，防波堤上层（图8（a））、下层（图8（b））水平格栅板所受波浪点压力分布随相对波高H/h的变化情况。之所以研究相对板宽B/L=0.31时上、下层水平格栅板所受波浪点压力随相对波高H/h的变化情况，是因为当相对板宽B/L位于0.3附近时，上、下水平格栅层板所受波浪点压力均相对较小，对实际工程中防波堤的局部稳定性有利。

从图8（a）可以看出防波堤上层水平格栅板所受波浪点压力基本也是以防波堤上层板中点对称分布，且在防波堤末端波浪点压力值均有略微上扬的趋势，即防波堤末端上层水平格栅板所受波浪点压力值均略大于防波堤最前端的波浪点压力值，这可能是由于防波堤后方存在竖直实体挡板，当波浪传播至防波堤末端时，波浪必须向上溢出，从而导致其波浪点压力值略有增大所致。此外，从图8还可看出，透空格栅板式防波堤上、下层水平格栅板所受波浪点压力均随相对波高H/h的增加而增加，这是因为波能正比于波高的平方，但试验水深h= 0.5 m保持不变，所以，当防波堤的相对波高H/h增加时，上、下层水平格栅板所受波浪点压力剧烈增大。

图8 防波堤上、下层板点压力分布随相对波高H/h的变化情况

图9描述了透空格栅板式防波堤所受波浪水平总力（图9（a））和垂直总力（图9（b））随相对波高H/h的变化情况。从图中可看出，防波堤所受波浪水平和垂直总力均随相对波高H/h的增加而增加，且基本呈线性关系。通过水平波浪总力和垂直波浪总力的对比可发现，防波堤所受垂直波浪总力要比水平波浪总力大一个数量级，因此，相对波高H/h主要影响透空格栅板式防波堤的垂向受力。且防波堤所受垂直波浪总力基本为正负方向对称分布，这说明防波堤受力均匀，利于其整体稳定和安全，这可能是由于透空格栅板式防波堤上下结构沿中层水平格栅板比较对称所致。

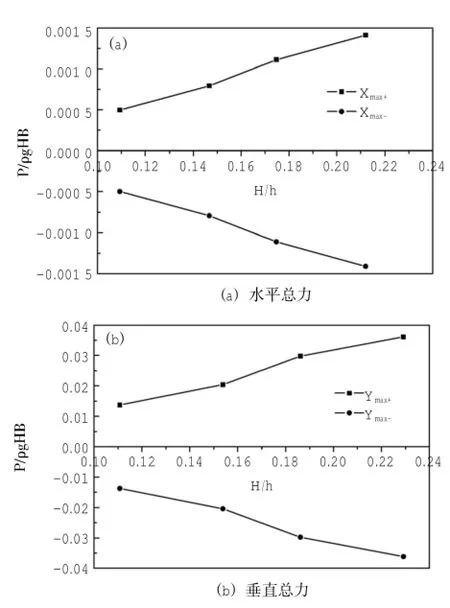
图9 防波堤所受波浪总力随相对波高H/h的变化情况

通过对比图5（出水堤），图7（平水堤），图9（淹没堤）可发现，防波堤的淹没深度对其受力有很大影响（Wu et al，2002；Rey et al，2011）。而平水情况时（图7）防波堤所受波浪总力最小；另外，考虑到防波堤与静水面齐平时的消浪效果最好（Liu et al，2008），且海上水位受到潮汐等作用，时刻都在变化，因此建议透空格栅板式防波堤在实际工程应用中采取上层水平格栅板与平均水位齐平的平水堤布置形式。

4 结论

从透空格栅板式防波堤的局部稳定性和整体稳定性出发，通过模型试验研究了其所受波浪点压力和波浪总力随相对板宽B/L、相对板间距S/h、相对波高H/h的变化情况。试验结果表明：

（1）下层水平格栅板所受波浪点压力在同一量级，分布规律均随防波堤宽度的延伸而逐渐减小，且受研究参数B/L，S/h，H/h的影响小。

（2）当相对板宽B/L和相对板间距S/h均不超过0.3时，透空格栅板式防波堤上、下层水平格栅板所受波浪点压力和波浪总力均相对较小，利于防波堤的局部稳定和整体稳定；而防波堤的中前端波浪点压力分布不规律，宜进行局部加固处理。

（3）透空格栅板式防波堤所受波浪水平和竖直总力基本呈对称分布，且相对板宽B/L较相对板间距S/h对防波堤所受波浪总力的影响大得多，相对波高H/h主要影响透空格栅板式防波堤的垂向受力。

（4）透空格栅板式防波堤的淹没深度h'和水平格栅板孔隙率G对其所受波浪总力有很大影响，当防波堤的布置形式为平水堤且水平格栅板孔隙率G相对较大时，其所受波浪总力最小，利于防波堤的整体稳定性。

Cheong H F,Patarapanich M,1992.Reflection and transmission of random waves by a horizontal double-plate breakwater.Ocean Engineering,18:63-82.

Chwang A T,1983.A porous wave maker theory.Journal of Fluid Mechanics,132:395-406.

Kweon H M,Choi Y H,2014.Effects of reverse waves on the hydrodynamic pressure acting on a dual porous horizontal plate.International Journal of Naval Architecture and Ocean Engineering,6:60-73.

Kweon H M,Oh S H,Choi Y H,2013.Experimental study on the method of estimating the vertical design wave force acting on a submerged dual horizontal plate.International Journal of Naval Architecture and Ocean Engineering,5:569-579.

Liu Y,Li Y C,Teng B,2007.Wave interaction with a perforated wall breakwater with a submerged horizontal porous plate.Ocean Engineering,34:2364-2373.

Liu Y,Li Y C,Teng B,et al,2008.Wave motion over a submerged breakwater with an upper horizontal porous plate and a lower horizontal solid plate.Ocean Engineering,35:1588-1596.

Neelamania S,Gayathri T,2006.Wave interaction with twin plate wave barrier.Ocean Engineering,33:495-516.

Patarapanich M,1984.Maximum and zero reflection from submerged plate.Journal of Waterway,Port,Coastal,and Ocean Engineering, 110:171-181.

Rey V,Touboul J,2011.Forces and moment on a horizontal plate due to regular and irregular waves in the presence of current.Applied O-cean Research,2(33):88-99.

Usha R,Gayathri T,2005.Wave motion over a twin-plate breakwater.O-cean Engineering,32:1054-1072.

Wu J H,Chwang A T,2002.Wave diffraction by a vertical cylinder with a porous ring plate,Journal of Engineering Mechanics,128:164-171.

Yip T L,Chwang A T,2000.Perforated wall breakwater with internal horizontal plate.Journal of Engineering Mechanics,126:533-538.

Yu X P,Chwang A T,1994.Water waves above submerged porous plate. Journal of Engineering Mechanics,120:1270-1282.

邱大洪，王学庚，1986.深水薄板式防波堤的理论分析.水运工程，4：8-12.

王国玉，王永学，李广伟，2005.多层水平板透空式防波堤消浪性能试验研究.大连理工大学学报，45（6）：865-870.

王晶，程永舟，杨小桦，等，2015.新型透空板式防波堤消浪效果试验研究.船舶力学，19（1-2）：86-94.

王科，高鑫，张犀，2011.平板及立板式防波堤散射波浪力研究.船舶力学，15（10）：1127-1133.

王志勇，朱浩，刘国宝，2012.双层水平板式防波堤结构箱型水平板研究.水运工程，472（11）：51-56.

（本文编辑:袁泽轶）

Experimental research of the wave force on the grille plate breakwater under the regular wave action

CHENG Yong-zhou1,2,CHANG Jia-fu1,YANG Xiao-hua1,HUANG Xiao-yun1,3
（1.School of HydraulicEngineering,Changsha University of ScienceandTechnology,Changsha 410004,China;2.Key Laboratory of Water and Sediment ScienceandWater Hazard Prevention,Changsha 410004,China;3.StateKey Laboratory of Hydrology-Water Resources and HydraulicEngineering,Hohai University,Nanjing 210098,China）

The porous grille plate breakwater is a new type structure of breakwater.To strengthen its practical engineering application,a physical model experiment research under the regular wave condition is performed to investigate the characteristics of wave point pressure and wave total forces on the breakwater.The results show that,the wave point pressure on lower horizontal grille plate is larger than that on the upper one,and the distribution near the front edge of the breakwater is unlawful.Meanwhile,the relative plate width B/L is rather significant than the relative plate spacing S/h which can be taken as the second place for the impact of wave total forces on the breakwater,and the relative wave height H/h almost only has effects on the vertical stress of the breakwater.Moreover,the results indicate that the wave total forces on the breakwater is minimum,which is most favorable to the stability of the breakwater when the upper grille plate is placed near the still water and the porous ratio of breakwater is relatively larger.

porous grille plate breakwater;horizontal grille plate;wave point pressure;wave total forces;stability

P731.22

A

1001-6932（2016）06-0641-08

10.11840/j.issn.1001-6392.2016.06.006

2015-08-01；

2015-10-23

国家自然科学基金（41176072,51109018）；交通运输部应用基础项目（2012-329-825-160）；湖南省自然科学基金（2015JJ2006）；水文水资源与水利工程科学国家重点实验室开放研究基金（2013491411）。

程永舟 （1974-），男，博士，教授，主要从事波浪、水流及边界相互作用方面研究。电子邮箱：chengyongzhou@163.com。