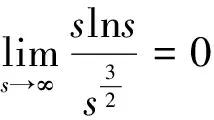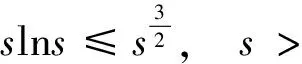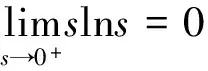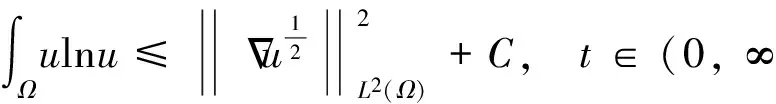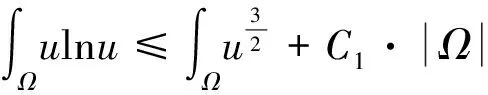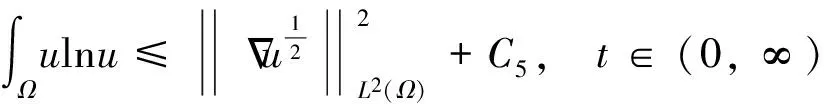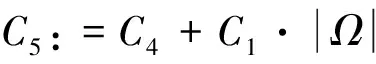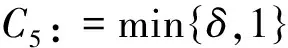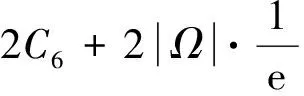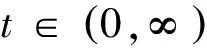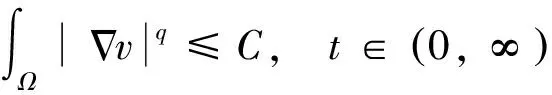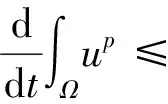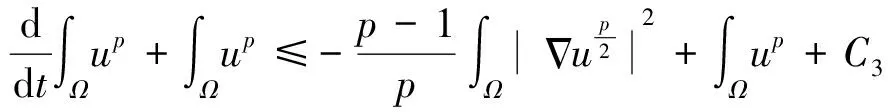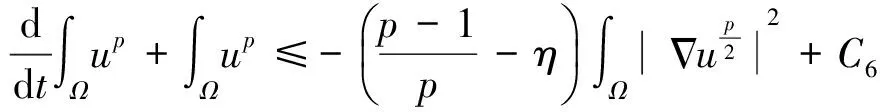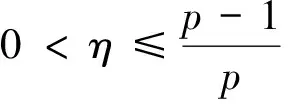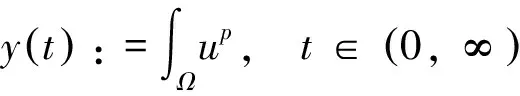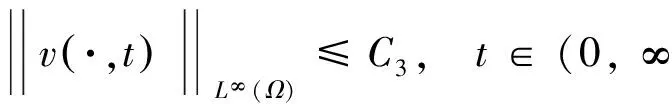具间接信号产出的二维趋向性模型古典解的整体存在性和有界性
王笑丹, 陶有山
(东华大学 理学院, 上海 201620)
具间接信号产出的二维趋向性模型古典解的整体存在性和有界性
王笑丹, 陶有山
(东华大学 理学院, 上海 201620)
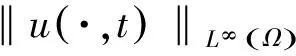
间接信号产出; 趋向性; 古典解; 整体存在性; 有界性
趋向性(chemotaxis)是由化学信号的浓度梯度引起的细胞的偏向运动,细胞偏向于朝化学信号浓度增加的地方移动.趋向性在许多生物环境中都有重要应用,如:细菌聚集、免疫反应、肿瘤诱导的血管生成等[1 3].近几十年,描述细胞响应于自身信号产出的集体行为的数学模型被广泛应用,不仅在生物学方面得到了深入研究,其数学特征也在多方面取得了深刻理解.
著名的趋向数学模型描述了细胞直接信号产出的集体行为,称为经典的Keller-Segel模型[4],具体表示为
其中:Ω⊂Rn是一个光滑有界区域,n表示空间维数;u表示细胞密度;v表示细胞产生的化学信号浓度;υ表示边界的外法向量;t表示时间.
假设化学信号的扩散远远快于细胞的扩散,这一假设在物理上是有意义的.故上述经典模型可用如下模型[5]逼近:
当空间维数n=1时,上述两个模型的解整体存在且一致有界[6].当n=2时,存在临界质量现象,即存在常数mc>0,当细胞质量m:=∫Ωu0
近些年,加拿大西部和美国森林中的山松甲壳虫,其生存和繁衍给森林造成了巨大损害.飞行中的甲壳虫落在松树上,啃噬树身形成树洞,在其中做窝并产卵,因此对松树造成极大危害.其间做窝的甲壳虫会释放一种化学物质来吸引飞行中的甲壳虫,到第二年幼虫长大离开树洞,会继续寻找松树做窝并产卵[11].
以此为背景,在上述Keller-Segel模型的基础上,本文对文献[11]提出的描述山松甲壳虫扩散和聚集行为的趋向模型[11]在具体的生物框架下进行简化,考虑如下趋向系统:
(1)

模型(1)的第一个方程表示飞行的甲壳虫密度随时间的变化情况,方程右边第一项是飞行甲壳虫的随机扩散项,第二项是chemotaxis项,表示飞行的甲壳虫向化学信号浓度增加的方向移动.模型(1)的第二个方程表示化学信号的随机扩散,化学信号由做窝的甲壳虫释放以及随时间衰减.模型(1)的第三个方程表示做窝的甲壳虫密度随时间的变化情况,右边第一项表示做窝的甲壳虫是由飞行的甲壳虫转化而来,第二项表示做窝的甲壳虫的死亡,δ为相应的死亡率.模型(1)的第四和第五个方程表示零黎曼边界条件和初值问题.
模型(1)与Keller-Segel模型存在本质区别[12]:Keller-Segel模型中的化学信号v是由细胞u直接产出的,而模型(1)是间接信号产出,飞行中的甲壳虫u转化为做窝的甲壳虫w,由做窝的甲壳虫w产生化学信号v.
本文假设(1)中的初始数据满足:
(2)
与二维空间中Keller-Segel模型的解有限时间爆破的性质形成鲜明对比,模型(1)的解不可能再有限时间爆破.更精确地说,有如下的整体解的存在性结果.


CGN‖φ‖L2(Ω)
(3)
在定理1的证明中,本文先建立飞行的甲壳虫密度u和做窝的甲壳虫密度w的Lp先验估计,再由Moser迭代推得u的L∞估计,进而由局部存在性引理和可延拓准则证得定理1.
如果假设初始细胞质量适当小,能进一步证明定理1中构造的整体古典解是一致有界的.具体地说,有如下结果.
定理2:假设n=2,δ>0,并假设初始数据满足(2),且满足

则存在常数C>0,使得(1)的整体古典解满足
‖u(·,t)‖L∞(Ω)≤ C,‖v(·,t)‖L∞(Ω)≤
C,‖w(·,t)‖L∞(Ω)≤C
对所有的t>0成立.
对于该定理的证明,本文在飞行甲壳虫初始质量适当小时,先建立做窝的甲壳虫密度w的L2一致先验估计,再建立飞行的甲壳虫密度u的Lp一致估计,然后同定理1的证法推得u的L∞一致有界性,进而根据常微分方程性质及椭圆方程最大值原理推得u和w的一致有界性.
1 整体解的存在性即定理1的证明
首先,考虑模型(1)的古典解的局部存在性.与古典的趋化模型的局部可解性类似,有下列关于(1)的局部可解性结论.
进一步,如果Tmax<∞,则有

证明:由于其证明与文献[13]中的证明类似,故在此略去.
根据引理1及延拓准则,要证明定理1中解的整体存在性,需要建立‖u(·,t)‖L∞(Ω)的先验估计.为此,先要对‖u(·,t)‖Lp(Ω)(1 引理2:模型(1)的古典解(u, v, w)满足 ‖u(·,t)‖L1(Ω)=‖u0‖L1(Ω):=m, t∈(0, Tmax). (4) 证明:对模型(1)的第一个方程关于x在Ω上积分,并利用分部积分及(1)中的零流边界条件可得 由此推得 ∫Ωu(x,t)dx=∫Ωu0(x). 从而引理2得证. 定理1证明的一个关键步骤是建立解分量w的L2先验估计. ∫Ωw2≤C(T), t∈(0,T). (5) (6) 这里用到了u和v的非负性. 再对(1)中第三个方程两边同乘w后积分,得到 ∫Ωwu-δ∫Ωw2≤∫Ωuw (7) 结合式(6)和(7)并利用Young不等式得 (8) (9) 则式(9)可写成 y'(t)≤C1y(t)+C2, t∈(0, T). 由此推得 根据w的L2估计及椭圆正则性理论,有如下的推论. (10) 证明:注意到v满足如下的椭圆边值问题 由估计(5)及椭圆方程的L2-理论有 ‖v‖W2,2(Ω)≤C1‖w‖L2(Ω) 据此,注意到空间维数 n=2,并根据Sobolev嵌入定理推得 从而推论1得证. (11) 证明:利用(1)中的第一个方程及Young不等式直接计算得 (12) 在上面最后一个不等式的推导中用到了估计(10). 根据G-N不等式,可以推得存在两个常数C2>0和C3>0,使得 (13) 从而 因此,利用Young不等式由式(13)推得 (14) =C5, 从而引理4得证. 得到u的Lp估计,根据模型(1)的第三个方程容易推得w的Lp先验估计. (15) 证明:由模型(1)的第三个方程,Young不等式及估计式(11)得 ∫Ωwp-1(u-δ w)= ∫Ωu wp-1-δ∫Ωwp≤ ∫Ωu wp-1≤ 在上面的推导过程中用到了δ和w的非负性.令 则上式可改写成 y′(t)≤y(t)+C3(T), t∈(0, T), 其中C3(T):=pC2(T).从而 即推论2得证. 定理1的证明:首先利用模型(1)的第二个方程,估计式(15)及椭圆的正则性理论有 再由引理1和可延拓准则推出结论.从而定理1得证. 引理5:假设s≥0,则存在常数C>0使得 证明:利用洛必达法则可得 因此存在常数A>0,使得当s>A时有 由此可得 又因为 slns≤C, 0≤s≤A. 综上可得 从而引理5得证. 引理6:假设n=2,δ>0,并假设(2)成立,则存在常数C>0使得模型(1)的古典解满足 (16) 证明:由引理5有 (17) 运用G-N不等式及Young不等式进一步处理式(17)倒数第二项 (18) 在u的初始质量适当小的假设下,建立w的与时间T无关的L2先验估计. 引理7:假设n=2,δ>0,并假设(2)成立,且满足 (19) 则存在常数C>0,使得模型(1)的古典解满足 ∫Ωw2≤C, t∈(0, ∞). (20) 证明:由引理3中式(6)和(7)的计算可知 在上式两边同时加上∫Ωulnu得 利用估计式(16)得到 (21) 再利用Young不等式,G-N不等式(3)及不等式(a+b)r≤2r-1(ar+br)(其中a>0,b>0,r≥1)对式(21)倒数第二项进行处理 根据假设(19) 从而有 令 则上式可改写成 :=C7, t∈(0, ∞), 推论3:假设n=2,δ>0,并假设(2)成立,且满足 (22) 证明:注意到v满足如下的椭圆边值问题 由估计(20)及椭圆方程的L2-理论有 ≤C2. 据此,注意到空间维数n=2,并根据Sobolev嵌入定理推得 从而推论3得证. 引理8:假设n=2,δ>0,并假设(2)成立,且满足 则对任意的p∈(1, ∞),存在常数C>0,使得模型(1)的古典解(u, v, w)满足 ∫Ωup≤C, t∈(0, ∞). (23) 证明:由式(12)及(22)得到 再由式(14)得到 (24) 综合式(23)和(24)得 在上式两边同时加上∫Ωup得 (25) 再利用Young不等式及式(24)处理式(25)倒数第二项得 其中η>0为任意常数.将上式代入式(25)得 令 则上式可改写成 y′(t)+y(t)≤C6, t∈(0, ∞), 根据常微分方程比较原理得 从而引理8得证. 定理2的证明:既然已得到了估计式(23),剩下的证明与定理1完全类似.因此,存在常数C1>0使得 (26) 接下来还需证明w的有界性,根据(26)及模型(1)的第三个方程得 据此再根据(1)中第二个方程及椭圆方程的最大值原理得 从而定理2得证. [1] ANDERSON A R A, CHAPLAIN M A J. Continuous and discrete mathematical models of tumor-induced angiogenesis [J]. Bull Math Biol, 1998, 60(5): 857899. [2] PAINTER K J. Continuous models for cell migration in tissues and applications to cell sorting via differential chemotaxis [J]. Bull Math Biol, 2009, 71(5): 11171147. [3] TINDALL M J, MAINI P K, PORTER S L, et al. Overview of mathematical approaches used to model bacterial chemotaxis Ⅱ: Bacterial populations [J]. Bull Math Biol, 2008, 70(6): 15701607. [4] KELLER E F, SEGEL L A. Initation of slime mold aggregation viewed as an instability [J]. J Theor Biol, 1970, 26(3): 399415. [5] HORSTMANN D. From 1970 until present: The Keller-Segal model in chemotaxis and its consequences Ⅰ [J]. Jahresberichte DMV, 2003, 105(3): 103165. [6] OSAKI K, YAGI A. Finite dimensional attractor for one-dimensional Keller-Segel equations [J]. Funkcialaj Ekvacioj, 2001, 44(3): 441469. [7] BILER P. Local and global solvability to some parabolic-elliptic systems of chemotaxis [J]. Adv Math Sci Appl, 1998, 8:715743. [9] NAGAI T, SENBA T. Behavior of radially symmetric solutions of a systemrelated to chemotaxis [J]. Nonlinear Analysis, 1997, 30(6): 38373842. [10] WINKLER M. Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system [J]. J Math Pures Appl, 2013, 100(5): 748767. [11] STROHM S, TYSON R C, POWELL J A. Pattern formaton in a model for Mountain Pine Beetle dispersal: Linking model predictions to data [J]. Bull Math Biol, 2013, 75(10): 17781797. [12] TAO Y S, WINKLER M. Critical mass for infinite-time aggregation in achemotaxis model with indirect signal production [J]. Journal of European Mathematical Society, accepted. [13] HORSTMANN D, WINKLER M. Boundedness vs. blow-up in a chemotaxis system [J]. J Differential Equations, 2005, 215(1): 52107. [14] TAO Y S, WINKLER M. Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity [J]. J Differential Equations, 2012, 252(1): 692715. Global Existence and Boundedness of Classical Solutions to a Two-Dimensional Chemotaxis Model with Indirect Signal Production WANGXiao-dan,TAOYou-shan (College of Science, Donghua University, Shanghai 201620) A chemotaxis model for the aggregative and dispersal behavior of the mountain pine beetle (MPB) is considered. The model involves three variables: the density of flying MPB u, the density of nesting MPB w and the concentration of chemical signals produced by the nesting MPB v. Firstly, some Lppriori estimates of u and w are obtained by employing the Gagliardo-Nirenberg inequality. Then, a L∞bound of u is founded via the Moser iteration argument, and thereby the global existence of classical solutions to the model is proved. Moreover, under the assumption that the initial mass of the flying MPB is less than a critical mass, it is shown that the classical solution is uniform-in-time bounded. indirect signal production; chemotaxis; classical solution; global existence; boundedness 16710444 (2016)060922-09 20151104 王笑丹(1989—),女,河南洛阳人,硕士研究生,研究方向为偏微分方程. E-mail:1033911032@qq.com 陶有山(联系人),男,教授,E-mail:taoys@dhu.edu.cn O 175.26 A


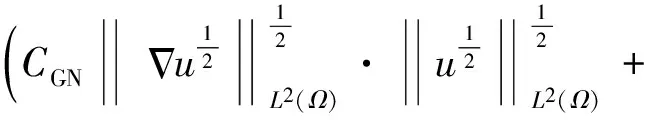
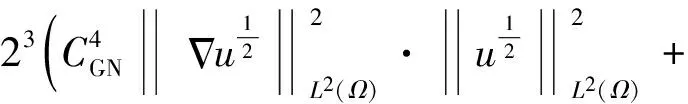


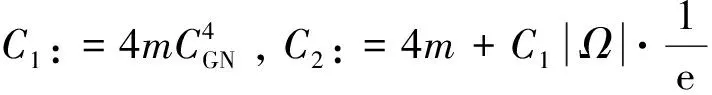



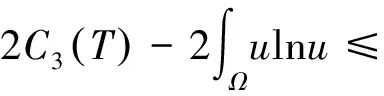


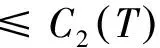

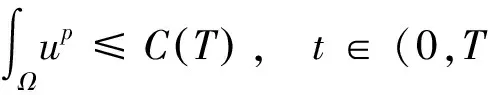
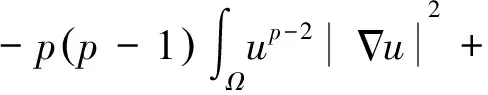
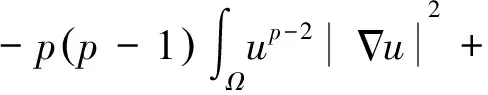

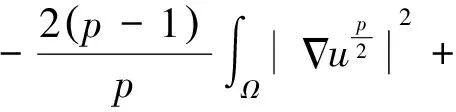
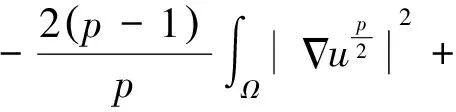
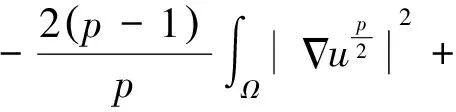



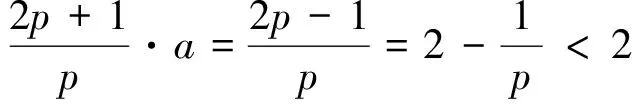

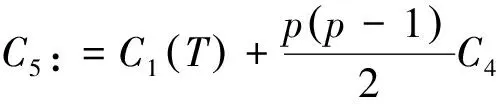


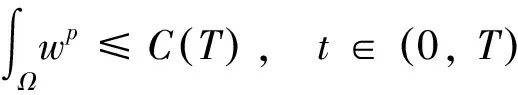
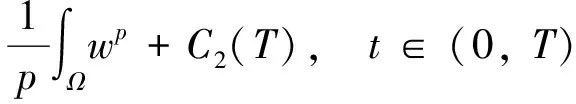

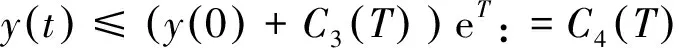
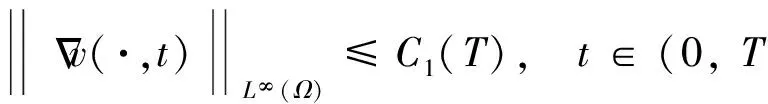

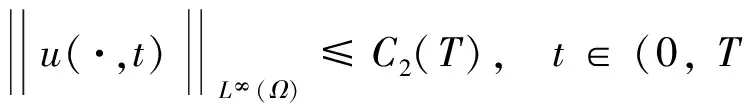
2 整体解的有界性即定理2的证明