正交非线性渗流定理

齐成伟

（重庆科技学院-石油与天然气工程学院，重庆 401331）

正交非线性渗流定理

齐成伟

（重庆科技学院-石油与天然气工程学院，重庆 401331）

将“正交幂比方程”代入不可压缩流体稳定渗流连续方程后得到了“正交低速非线性渗流控制方程”。正交低速非线性渗流控制方程是二阶非线性偏微分方程，故除“直流场”外，其符号解极难求得。综合运用场论和微分几何知识，对流场几何进行了定性分析，得到“正交非线性渗流定理：假设非线性渗流的等压面与流线正交，若流场为‘曲流场’，则相同条件下单相不可压缩或可压缩流体非线性渗流与单相不可压缩流体线性渗流的流线形状不同。进而，等压面形状亦不同。”以斯托克斯流动为类比，指出了非线性渗流的等压面与流线的不正交可能性。

渗流力学 流场几何 正交幂比连续方程 曲流场 流线曲率矢量公式 引理 复曲率公式 广密压裂

0 引言

如果油水地下渗流具有“低速非线性”，那么相同条件下的低速非线性渗流与线性渗流有何不同呢？

1 本构方程

描写低速非线性渗流之平行流的幂比方程［1］为：

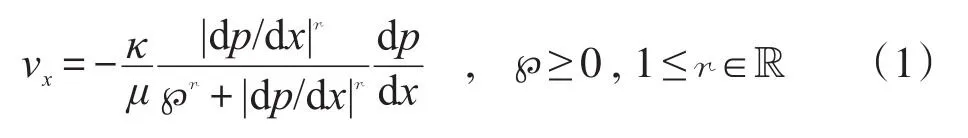
式中，v为流体渗流速率，m/s；κ为多孔介质渗透系数，m2；μ为流体动力黏度，Pa·s；p为流体压强，Pa；x（y、z）为Descartes坐标系的横（纵、竖）坐标（作为角标，示意方向），m；r为非线性指数，无量纲；℘为渐近线截距，Pa/m。

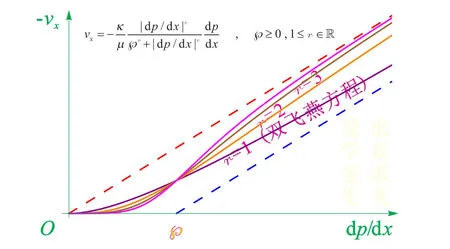
图1 低速非线性渗流本构方程

如图1所示：r控制vx～dp/dx曲线的形状；控制vx～dp/dx曲线的大小。

岩心渗流测试采用的圆管岩心夹持器或填砂圆管限定流动为平行流，或称一维流。无论是线性渗流还是非线性渗流，平行流的等压面与流线必然正交。对于线性渗流，二维流、三维流的等压面与流线正交。对于非线性渗流，除“柱径流”外的二维流、除“球径流”外的三维流的等压面与流线也一定正交吗？未经实验，不得而知。

假设低速非线性渗流的等压面与流线正交，则其渗流速度与压强梯度之间的本构关系可写为“正交幂比方程”。分量形式的正交幂比方程为：

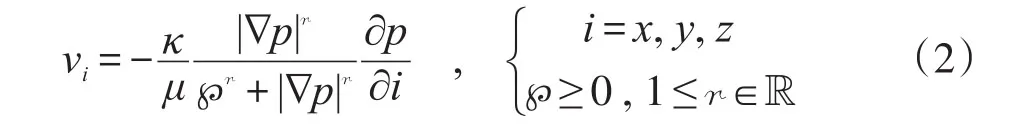
矢量形式的正交幂比方程为：

2 控制方程

将式（3）代入不可压缩流体稳定渗流连续方程

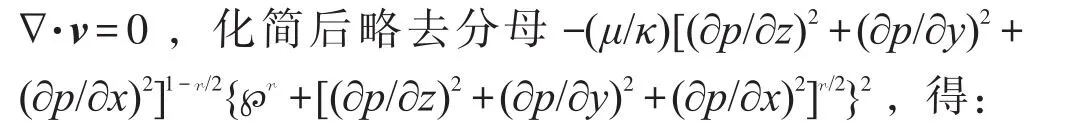
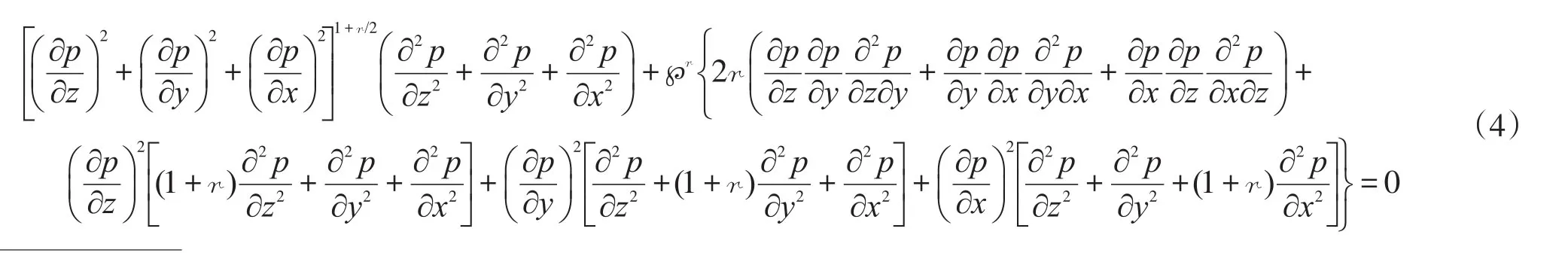
称式（4）为“正交幂比连续方程”或“正交低速非线性渗流控制方程”。读者可以验证：r=1情况下的平行流压强函数p=[qμ/(4κw)]{1+[1+8κw℘/(|q|μ)]1/2}|x|（q为裂缝汇（或源）强度，m2/s；w为带形地层宽度，m）、柱径流压强函数（文献［1］式（4），[]内的q替换为|q|，q为二维点汇（或源）强度，m2/s）和球径流压强函数（文献［1］式（6），[]内的Q替换为|Q|，Q为三维点汇（或源）强度，m3/s）是方程（4）的符号解。

3 渗流场论

3.1 涡矢量场

为了普适性，将正交非线性渗流本构方程写为：

式中，g()为可微函数；g(|∇p|)为非线性系数函数，无量纲。强令g()=1，则式（5）退化为线性渗流本构方程，即Darcy's law。式（5）囊括Forchheimer's law。

正交非线性渗流涡矢量场为：

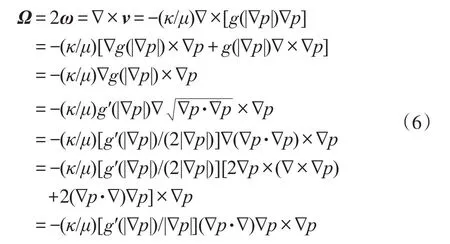
式中，Ω为渗流涡矢量，s-1；ω为渗流角速度，rad/s。

式（6）中，(∇p·∇)∇p×∇p的Descartes坐标形式为：

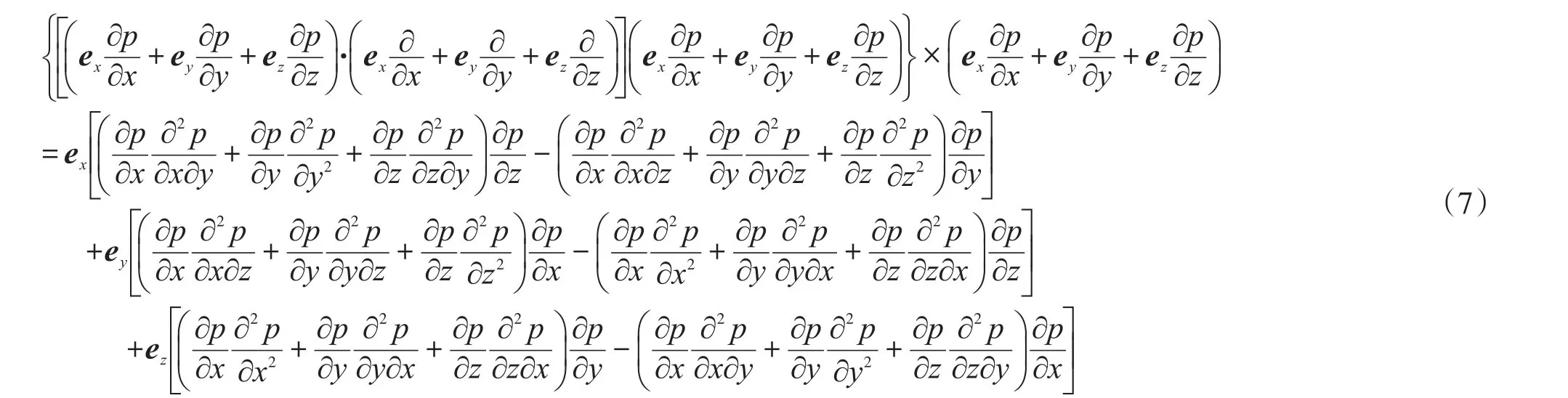
3.2 流线曲率矢量场

记流线函数为：

将式（8）转化为参数方程形式，如：

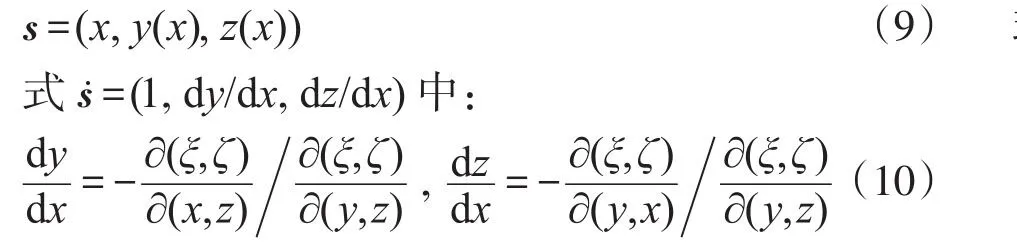
式（5）与v=(CⅠ/ρ相结合，得：

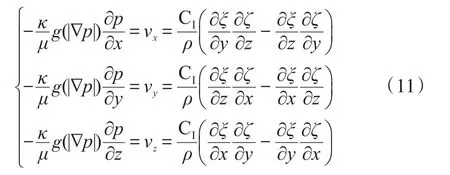
式中，ρ为流体质量密度，Kg/m3。

将式（11）代入式（10），得：

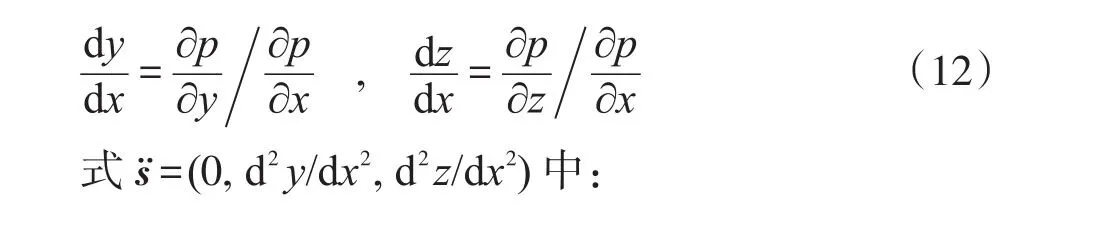
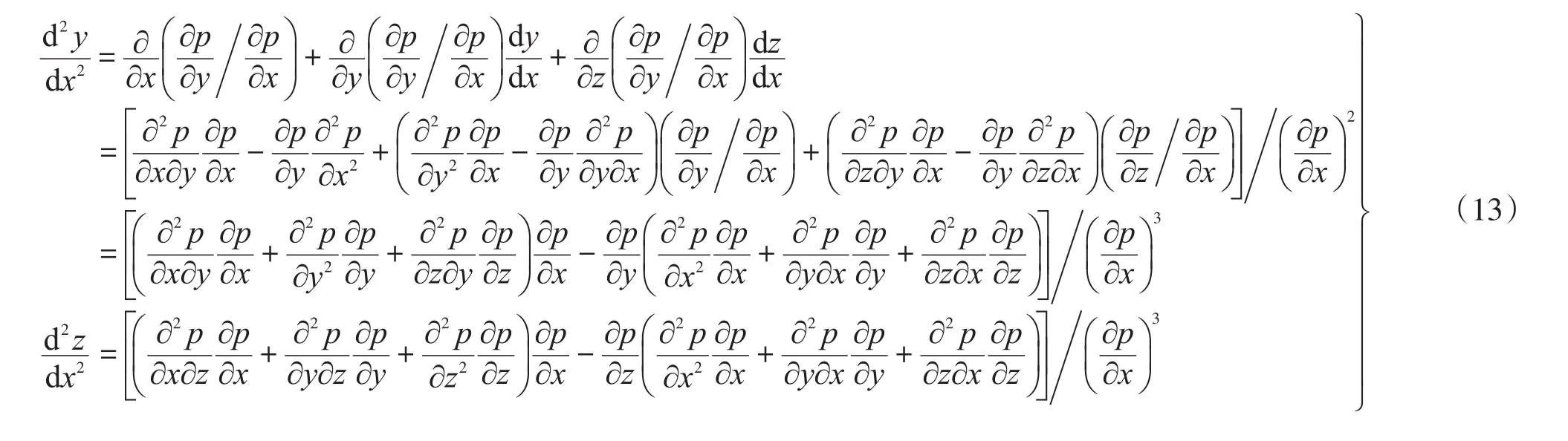
对比式（13）与式（7），知：

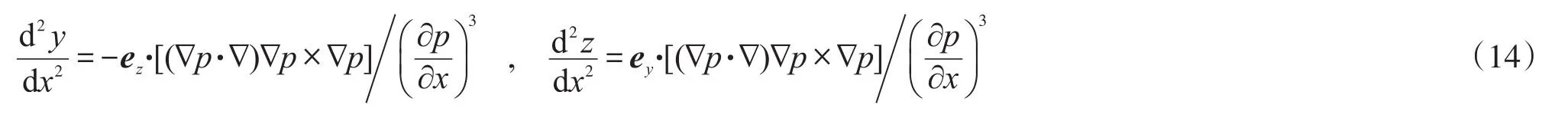
据式（14）、式（12）、式（7）、式（6），知流线曲率矢量场为：

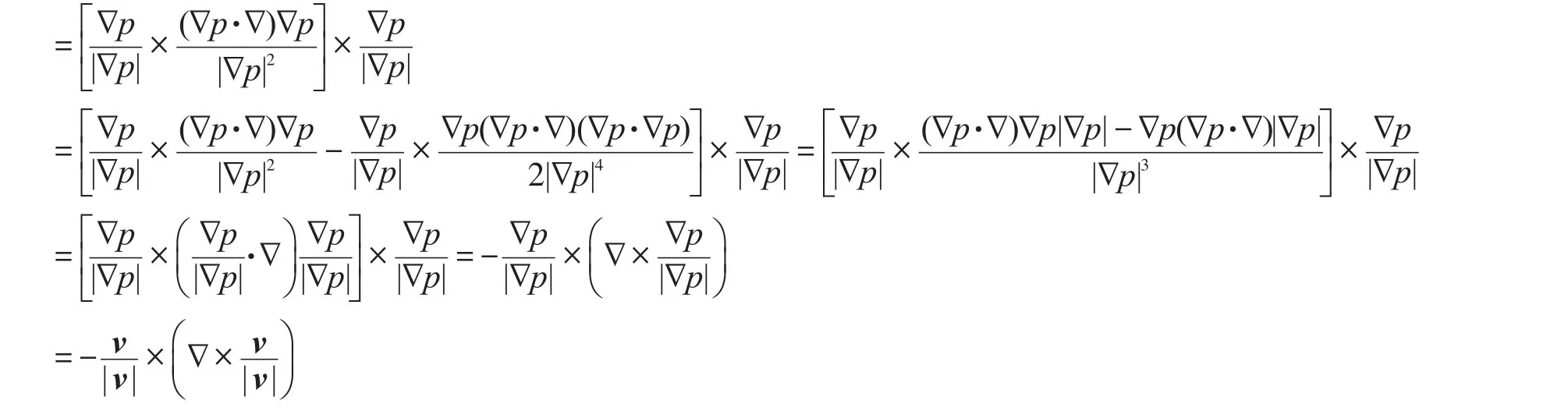
式中，kξ∩ζ为流线曲率矢量，m-1。

式（15）倒数第2行显示：正交非线性渗流的流线曲率矢量是归一化压强梯度与其旋度的负矢积。

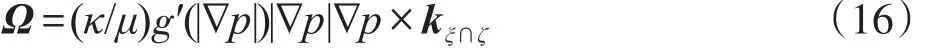
式（16）显示：除平行流、柱径流和球径流（下称“直流场”，）外（下称“曲流场”，，式（5）所描述的渗流速度场为有旋场。

引理：正交非线性渗流之直流速度场为无旋场；正交非线性渗流之曲流速度场为有旋场。

3.3 平面势流流线曲率

敬请读者欣赏无限大等厚均质各向同性水平地层内环形裂缝群激发的线性渗流场的流线曲率绝对值密度图。

对于二维问题，式（7）退化为：

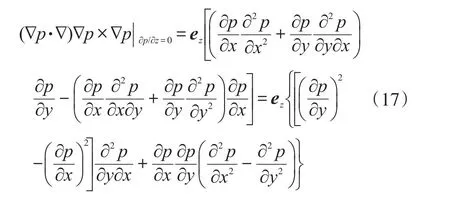
记平面稳态流速场复位势与复坐标的函数关系为：

式中，f()为解析函数；φ为势，m2/s；ψ为流，m2/s。对于渗流场，φ=κp/μ。注意：解析=共形。

根据Cauchy-Riemann条件［2］，知：

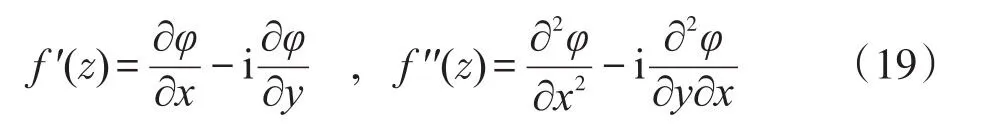
显然，用式（19）凑出式（17）的{}部分是可能的。尝试后发现：

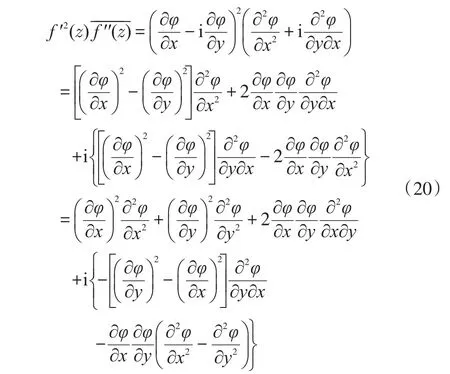
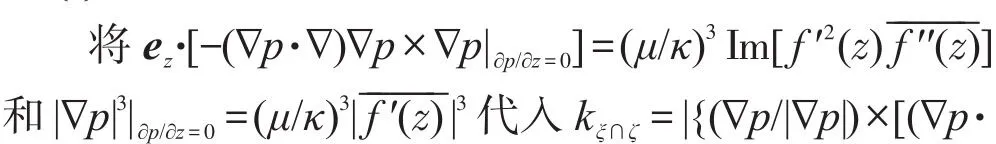
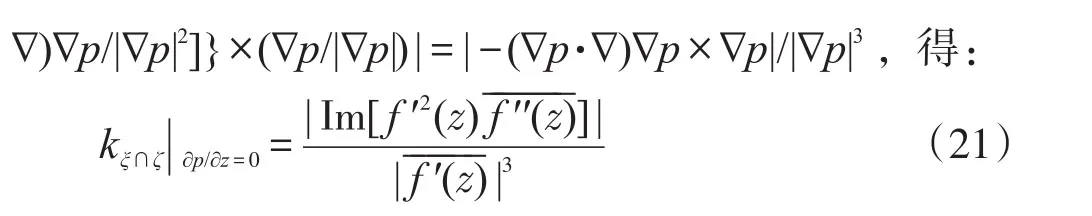
可将式（21）改写为：

式（22）规定：流线向左偏转，流线曲率为负；流线向右偏转，流线曲率为正。

非常幸运，平面势流等势线曲率恰为：

可将kφ+ikψ称为“平面势流‘复曲率’”，记为k，译为“complex curvature”。于是，复曲率公式为：环形裂缝群复势通式［3］为：

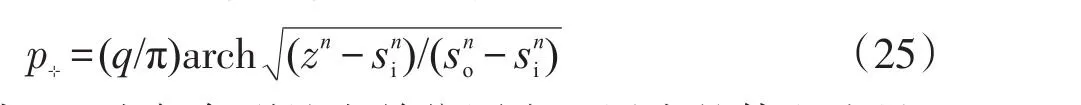
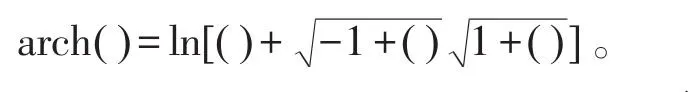
将式（25）代入式（24）后做替换z→x+iy，得：

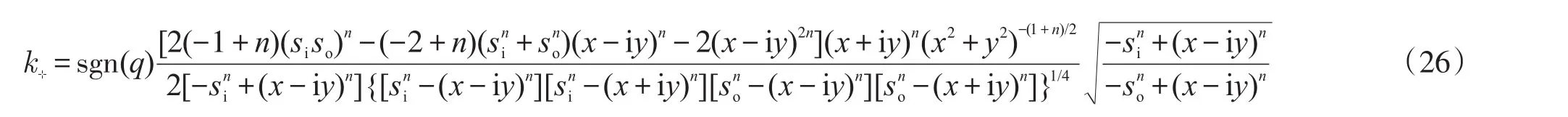
令si/so=1/3，根据式（26）绘得等势线曲率密度图（向ɷ花）和流线曲率绝对值密度图（背ɷ花），见图2。

图2 环形裂缝群线性渗流复曲率密度图

4 流线形状

假设流场边界形状相同且流入流出端面皆为等压面的均质各向同性多孔介质内单相不可压缩或可压缩流体非线性渗流与单相不可压缩流体线性渗流的流线形状相同，或称流线重合，则同一坐标点处的渗流速度方向一致，即：

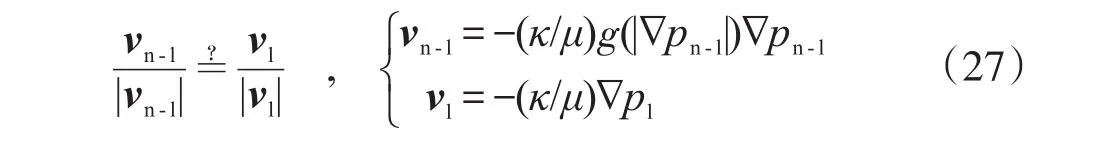
式中，角标n-l、l依序示意非线性渗流、线性渗流。

将质流密度ρn-lvn-l,ρlvl代入散度定理，得：

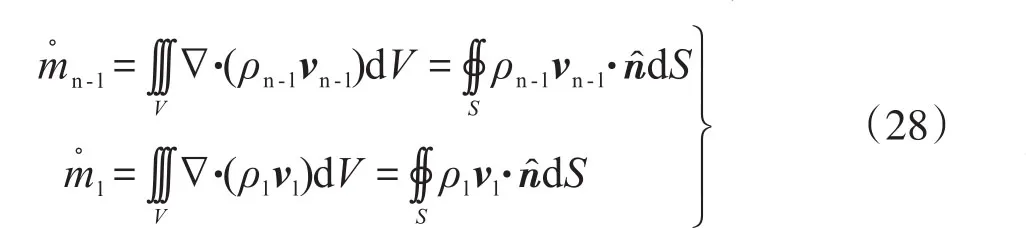
式中，m。为流场内某一口井或某几口井的质量流量，Kg/s；V为仅包含该口井或该数口井的任一控制体的体积（作为下标，表示积分区），m3；S为相应的控制面的面积（作为下标，表示积分域），m2；n^为控制面上的单位外法矢量，无量纲。

式（29）与式（27）相结合，得：

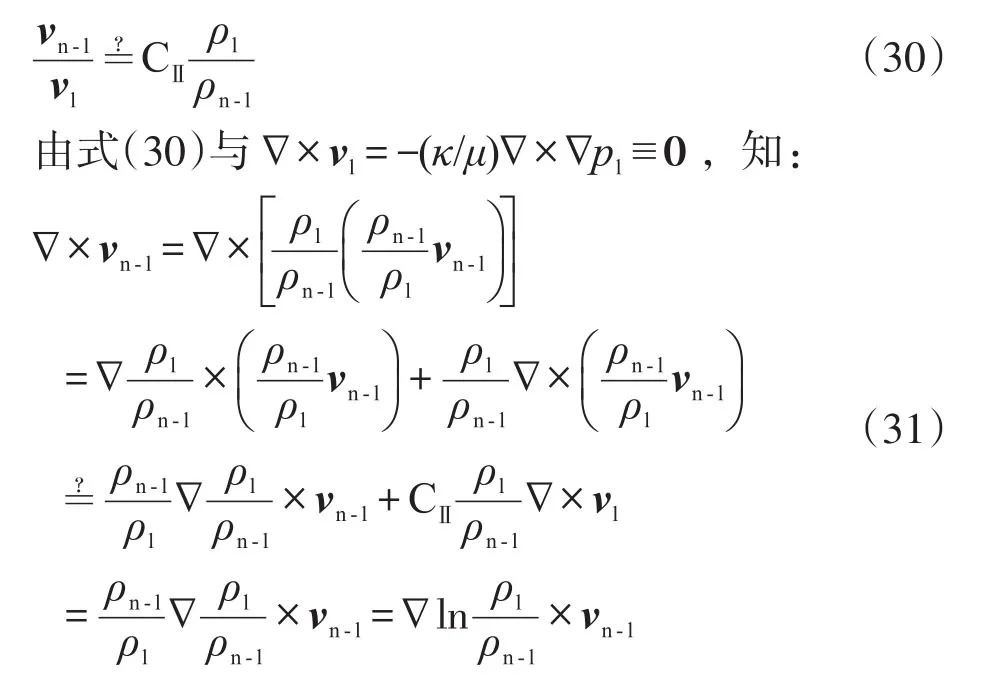
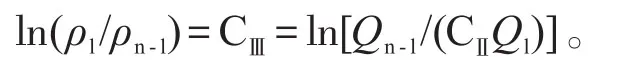
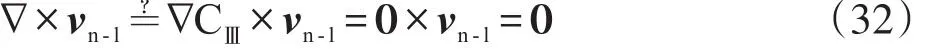
对于单相可压缩流体非线性渗流与单相不可压缩流体线性渗流而言，ln(ρl/ρn-l)≠CⅢ。将正压条件ρn-l=ρn-l(x,y,z)=ϱn-l(pn-l)代入式（31）后再结合式（5），得：

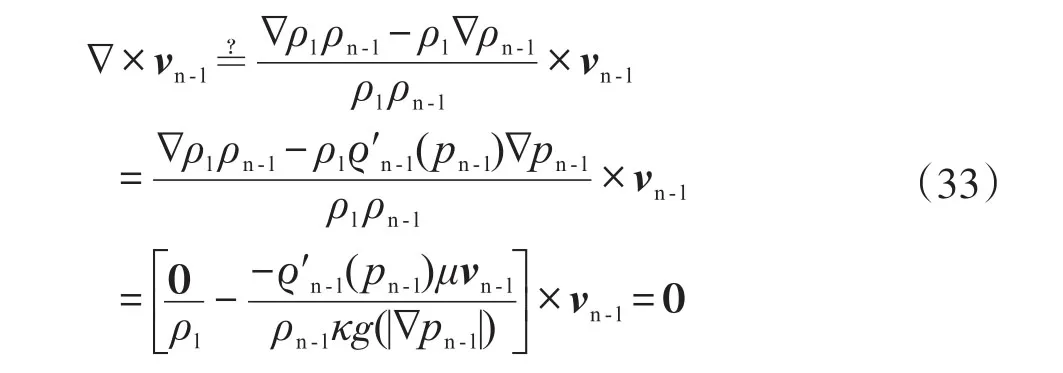
然而，式（16）显示，对于曲流场，有：

综上，对于相同条件下的曲流场，式（32）、式（33）与式（34）或式（16）矛盾，故式（27）所表述的“流线重合假设”与引理矛盾。因而，对于曲流场，流线重合假设不成立，即“若

正交非线性渗流定理：假设非线性渗流的等压面与流线正交，若流场为曲流场，则相同条件下单相不可压缩或可压缩流体非线性渗流与单相不可压缩流体线性渗流的流线形状不同。进而，等压面形状亦不同。

5 缘何正交

流体力学里的不可压缩Perfect fluid“绕球无旋层流”和不可压缩Newtonian fluid“绕球有旋层流”或可带来启示。下面回顾原点处半径为r的小球对流速场v∞=v∞ex的影响。此处，v表示真实流动速度。对于单相不可压缩流体，ρ为实正常数，故不妨令CⅠ=ρ。

5.1 绕球无旋层流

无旋场必是有势场。线性流动与线性渗流具有相同的控制方程，即∇2φ=0。对于无多孔介质的流动，φ≠κp/μ。因已忽略重力，故等势面与等压面重合。

结合边界条件求方程∇2φ=0的符号解，取ζ=arc tan(z/y)后结合ξ(x,0,0)=0求方程-∇φ=v=∇ξ×∇ζ的符号解，得绕球无旋层流的势函数和流线函数：

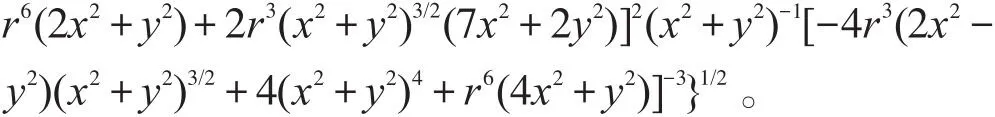
根据式（35）绘得绕球无旋层流流网图，见图3。

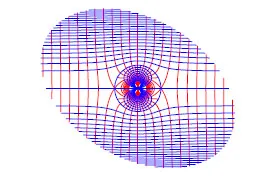
图3 绕球无旋层流流网纵对称面图

如图3所示：前驻点［4］(-r,0,0)和后驻点(r,0,0)外的空间内，绕球无旋层流的等势面与流线处处正交。

5.2 绕球有旋层流

本文仅重述Stokes flow，而不重述Oseen flow。

不可压缩Newtonian fluid的Stokes equations为：

结合边界条件求方程组（36）的符号解，得绕球有旋层流的压强场函数和速度场函数：

点没有角速度。

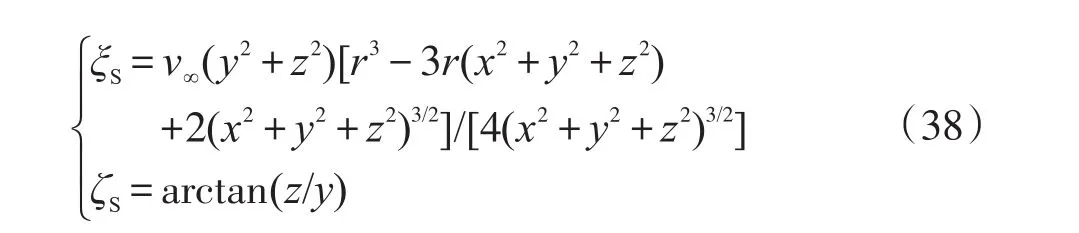
根据式（37）和式（38）绘得绕球有旋层流流场图，见图4。注意观察：球外曲流线两次斜穿同一等压面。

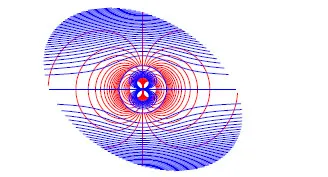
图4 绕球有旋层流流场纵对称面图

等压面与流线正交的数学条件为∇pS×vS=0。因为

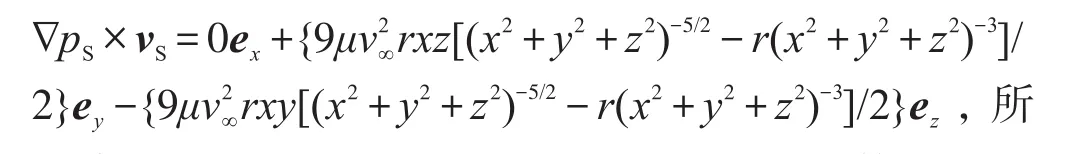
以直线y=0,z=0和平面x=0外的空间内等压面与流线处处不正交。

6 结束语

正交非线性渗流定理表明：无限大等厚均质各向同性水平地层内具有无限导流能力且铅垂贯穿地层的有限长无宽直裂缝激发的正交非线性渗流场的流线不是以裂缝端线等高点为焦点的双曲线，等压面也不是以裂缝端线为焦线的椭圆柱面。拟共形？

非线性渗流的等压面与流线是否正交，可通过测试具有非线性渗流特征的等厚均质各向同性水平岩板内二维曲流场的等压面与板缘壁面是否正交来判定。若不正交，谁能极之？不管是否正交，为理论非线性渗流力学奠基仅需一个曲流压强场显函数。

［1］齐成伟.低速渗流“非线性”探测构想［J］.天然气技术与经济，2015，9（6）：37-38.

［2］齐成伟.平面稳态流速场运动学通式［J］.天然气技术与经济，2013，7（6）：27-28.

［3］齐成伟.环形裂缝群激发的渗流场之运动学分析［J］.特种油气藏，2014，21（4）：101-104.

［4］齐成伟.致密油藏水力碎裂区是“死油区”［J］.内蒙古石油化工，2015，41（17）：146-147.

（编辑：李臻）

A

2095-1132（2016）06-0016-06

10.3969/j.issn.2095-1132.2016.06.005

2016-10-16

2016-12-16

齐成伟（1983-），硕士，实验师，从事流体力学、油气水渗流力学基础理论研究。E-mail：1261621@qq.com。