基于Boussinesq方程的陡峭礁坪上波浪传播变形数值模拟
黄英丽,王国玉,房克照,陈 戈
(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
基于Boussinesq方程的陡峭礁坪上波浪传播变形数值模拟
黄英丽,王国玉,房克照,陈 戈
(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
为了探究应用基于二阶完全非线性Boussinesq方程开发的Funwave-TVD波浪模型模拟波浪在陡峭礁坪上传播变形的可行性,在采用试验及已有文献成果进行可行性验证的基础上,利用该模型模拟了波浪在陡峭礁坪上的传播变形过程,分析了不同波浪要素及不同水深情况下波浪在陡峭礁坪上的传播规律。结果表明:当波高与水深的比值超过一定值时,波浪发生破碎,波高迅速减小;对于深水情况下的陡峭礁坪地形,当波浪离开礁坪坡脚的水平距离为4倍入射波长及更远时,礁坪上的平均波高可降低为稳定值。
波浪传播;传播变形;陡峭礁坪;Boussinesq方程;Funwave-TVD
我国拥有众多珊瑚礁,主要分布在海南岛和台湾岛的沿岸以及南海诸岛。珊瑚礁作为珍贵的资源,对国防事业、交通运输业和旅游业等都具有非常重要的价值。近年来,我国在珊瑚礁上建设了一定数量的工程,随着礁坪上建设工程的增多,对波浪在珊瑚礁上传播规律的研究日显重要,同时也能为珊瑚礁上工程的规划、设计和施工建设等提供理论支撑。
国内外学者大多采用物理模型试验研究波浪在珊瑚礁上的传播变形,且主要集中在缓坡上。赵子丹等[1]对波浪在珊瑚礁及台阶地形上传播的研究现状进行了综述,指出由于珊瑚礁水深剧变,可将珊瑚礁地形简化成无限长台阶地形进行探讨,并提出发展高阶非线性理论以用于解释高阶谐波分量。黎满球等[2]根据实际测得的海浪数据资料,在考虑风对海浪的影响情况下,分析了波浪在礁坪上传播时的衰减特点和波浪能量转移特性。Roeber等[3]利用试验模型探究了珊瑚礁上的波浪传播过程,并扩展了Boussinesq方程。梅弢等[4]利用水槽试验研究了波浪在珊瑚礁坪上的传播规律,结果发现当入射波浪较大时,传播过程中波浪会在礁缘处破碎,并继续向坪内传播,并达到波面稳定状态,礁坪上的波浪衰减迅速。柳淑学等[5]采用断面物理模型试验研究了珊瑚礁地形,发现对于规则波,入射波高较小时,波浪受非线性作用比较小,波形比较稳定;当入射波高增大时,波浪发生破碎,但破碎位置出现在同一位置。郑金海等[6]认为可以基于布拉格共振的基本思想,通过设计堤顶高程低于平均低潮位的防浪堤来达到消浪目的,而绝大多数珊瑚礁礁盘与平均低潮位水位相近,该想法为研究珊瑚礁地形提供了新思路。
数值模型方面,李炎保等[7]利用数值模拟和物理试验分析了波浪在1∶1.5陡坡上的传播变形,数值模拟采用标记单元法,并采用“台阶镜像法”处理坡面对波浪的反射,得到了波浪传播变形过程。刘海清等[8]采用N-S方程作为基本方程,利用二维数值波浪水槽模拟了波浪在台阶上的传播过程。Douillet等[9]运用流体动力学耦合模型研究了新喀里多尼亚的西南潟湖里悬浮物质的移动情况,发展并验证了悬浮物质移动的数值模型,这为研究潟湖里的波浪运动提供了新的思路。Yao等[10]基于一维完全非线性Boussinesq方程,对不同珊瑚礁上波浪产生的波面和波高变化进行了数值模拟研究。祁国军等[11]通过源函数造波法研究了波浪爬高与波陡和坡比之间的关系,发现当波浪波陡较小时,在相同糙率条件下,地形坡度越缓,波浪爬高衰减系数越小;而波陡较大时,随着地形坡度变缓,波浪爬高衰减系数先增后减。房克照等[12]建立了基于高阶Boussinesq方程的波浪传播数学模型,控制方程采用有限差分和有限体积法混合求解,并进一步模拟了孤立波在潜礁上的传播变形。
目前,关于礁坪上波浪传播变形的数值模拟工作大都局限于坡度较缓的情况,如Yao等[10]模拟的最大坡度为1∶6。实际上,陡峭礁坪在珊瑚礁群中占有相当大的比例,因此陡峭礁坪上波浪传播变形规律的研究越来越受到学者的关注,而Boussinesq类方程都具备色散性和非线性的特点,可应用于模拟陡峭礁坪地形上的波浪传播。本文将珊瑚礁简化成陡坡,选取基于Boussinesq方程并具有TVD性质的完全非线性数值模型——Funwave模型对波浪在陡峭礁坪地形上的传播变形规律进行了数值计算,并给出了波浪达到稳定安全波高时波浪离开珊瑚礁底的距离。
1 Funwave-TVD波浪模型简介
Kirby等[13]基于完全非线性Boussinesq波浪模型在1998年创立了Funwave模型,此后很多学者对模型的改进进行了研究,本文采用的Funwave-TVD波浪模型是美国Delaware大学Shi等[14]在前人Funwave模型基础上改进的版本,该模型基于Chen[15]建立的Boussinesq波浪方程,在求解和捕捉波浪破碎和干湿界面处理等方面进行了必要的改进和创新,能够综合考虑波浪的折射、绕射、反射和变浅效应等的影响,适用于模拟波浪在较为复杂地形上的传播变形问题。
1.1 控制方程
Funwave-TVD波浪模型控制方程如下:
(1)
(2)
式中:η为波表面高度;ηt为η对时间的偏导数;h为静水深;d为当地水深;uα为z=zα处的水质点的水平速度矢量,zα随时间变化;ζ、β为常数[16];u2为平均水深下的垂直方向速度,色散性精确到o(μ2),其中μ=kh;)为水平梯度算子。该控制方程是Chen[15]在Wei等[17]建立的Boussinesq波浪模型的基础上完善的。
1.2 波浪破碎和底部摩擦阻力项的处理
Funwave-TVD波浪模型中波浪破碎的处置方法采用Tonelli等[18]的研究成果。Tonelli等[18]利用带有TVD格式的非线性浅水波浪方程模拟了移动水跃波,当弗劳德数超过一定数值时,就利用非线性浅水波浪方程取代完全非线性Boussinesq方程进行计算,破碎指标受坡度的影响很大,目前尚未找到严格的理论解,Tonelli等[18]建议破碎控制项为深水波高与水深(波浪行进到某点的静水深)的比值为0.8。
考虑到水体在运动时与底部发生了摩擦,数值模拟中考虑底部摩阻项,具体方法是在动量方程中加入底部摩阻衰减项,表达式如下:
(3)
(4)
式中:FB、GB分别为作用在某水质点水平速度和垂直速度方向上的分力;fw为底部摩擦阻力系数;uα、vα分别为某水质点的水平速度分量和垂直速度分量。
2 模型验证
2.1 已发表文献成果验证
Yao等[19]早在2009年利用试验模型模拟了礁坪地形上波浪的传播规律,给出了不同坡比、不同波浪要素下波浪的传播规律。将他们的试验结果和数值模拟结果作为验证Funwave-TVD波浪模型(以下简称本文模型)模拟结果的数据资料,来验证本文模型模拟结果的准确性。
Yao等[10]在新加坡南洋理工大学的水动力学实验室开展了此次试验。水槽长36 m,宽0.55 m,深0.60 m,试验中考虑两种情况,一种是理想礁坪,即礁坪顶部平滑;一种是带有山脊模型的礁坪。本文与其理想礁坪地形状态下的两组试验结果进行对比(试验1和试验2),如图1和图2所示(图中x为相对礁坪坡脚的位置,x=0 m为礁坪起始点)。
由图1可见,对于试验1,离造波机较近和较远处,本文模型模拟的平均波高曲线与文献[10]试验结果吻合较好,在礁顶附近略有偏差;而试验2本文模型模拟结果与文献[10]试验结果吻合较好。由图2可见,试验1本文模型模拟的平均水面曲线与文献[10]试验结果吻合较好;对于试验2,本文模型模拟结果在礁顶前与文献[10]试验结果基本吻合,在礁顶后稍有偏差,但是趋势较符合。
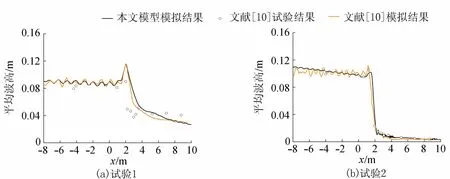
图1 平均波高对比
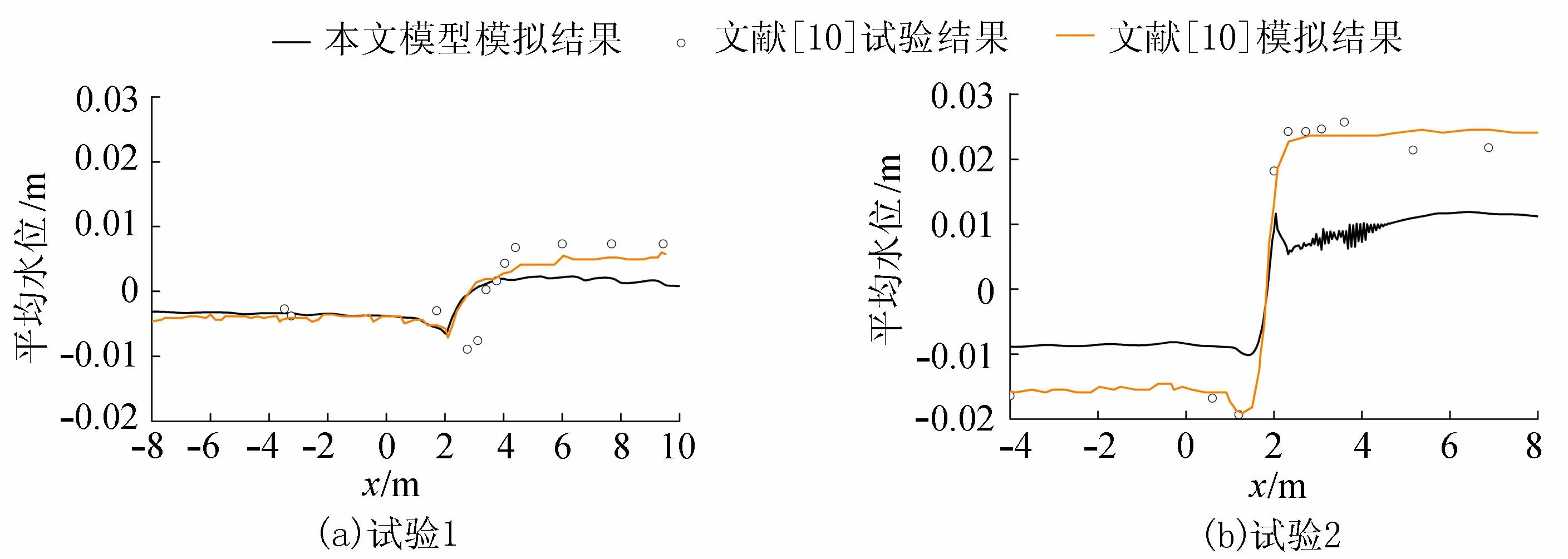
图2 平均水位对比
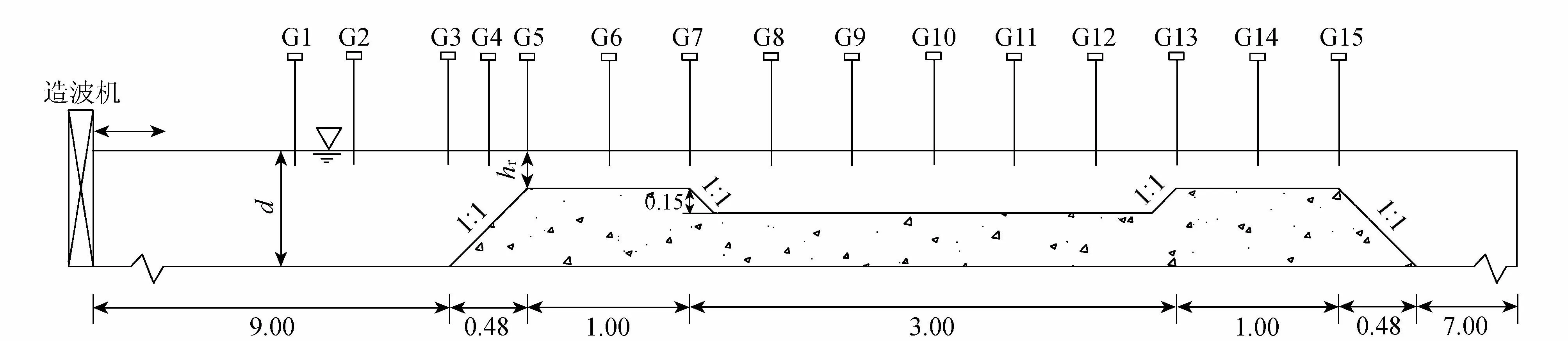
图3 验证试验礁坪模型剖面示意图(单位:m)
总的来说,本文模型模拟结果和Yao等[10]的模拟结果还是比较吻合的,因此可以初步判断本文模型可以用来模拟礁坪地形。
2.2 试验验证
为了进一步探究本文模型是否适用于陡峭礁坪,笔者在大连理工大学海岸和近海工程国家重点实验室里布置水槽进行了试验研究。水槽地形如图3所示,4个斜坡段的水平方向长度依次为0.48 m、0.15 m、0.15 m、0.48 m,坡度均为1∶1,礁坪上水深hr=0.02 m,共分布有15个浪高仪测点,浪高仪G1~G15相对礁底的距离分别为-0.58 m、-0.48 m、0.02 m、0.25 m、0.50 m、1.00 m、1.50 m、2.00 m、2.50 m、3.00 m、3.50 m、4.00 m、4.50 m、5.00 m和5.50 m。试验主要波浪要素为:水深d=0.50 m,周期T=0.8 s,入射波高H0=0.02 m、0.03 m。因为实验室的礁坪模型采用水泥制作,表面光滑,摩擦系数极小,为了和实验室试验情况进行对比,采用本文模型模拟时,只考虑理想情况下的礁坪,即不考虑海床底摩擦,底摩擦系数为0。
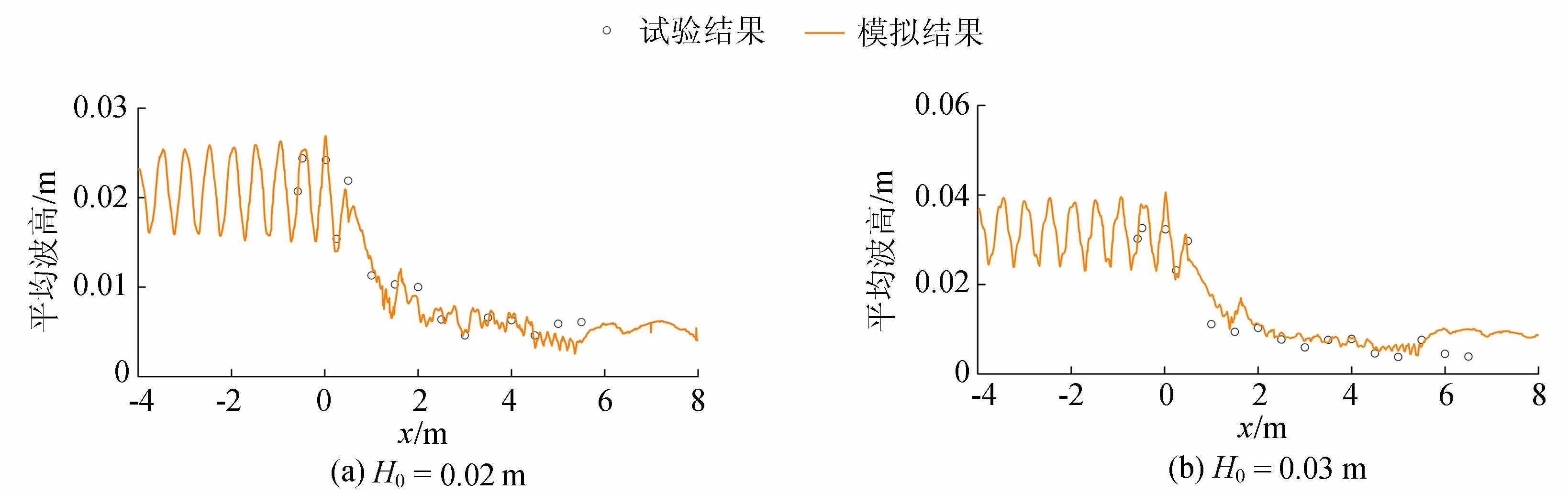
图4 平均波高试验结果和模拟结果对比
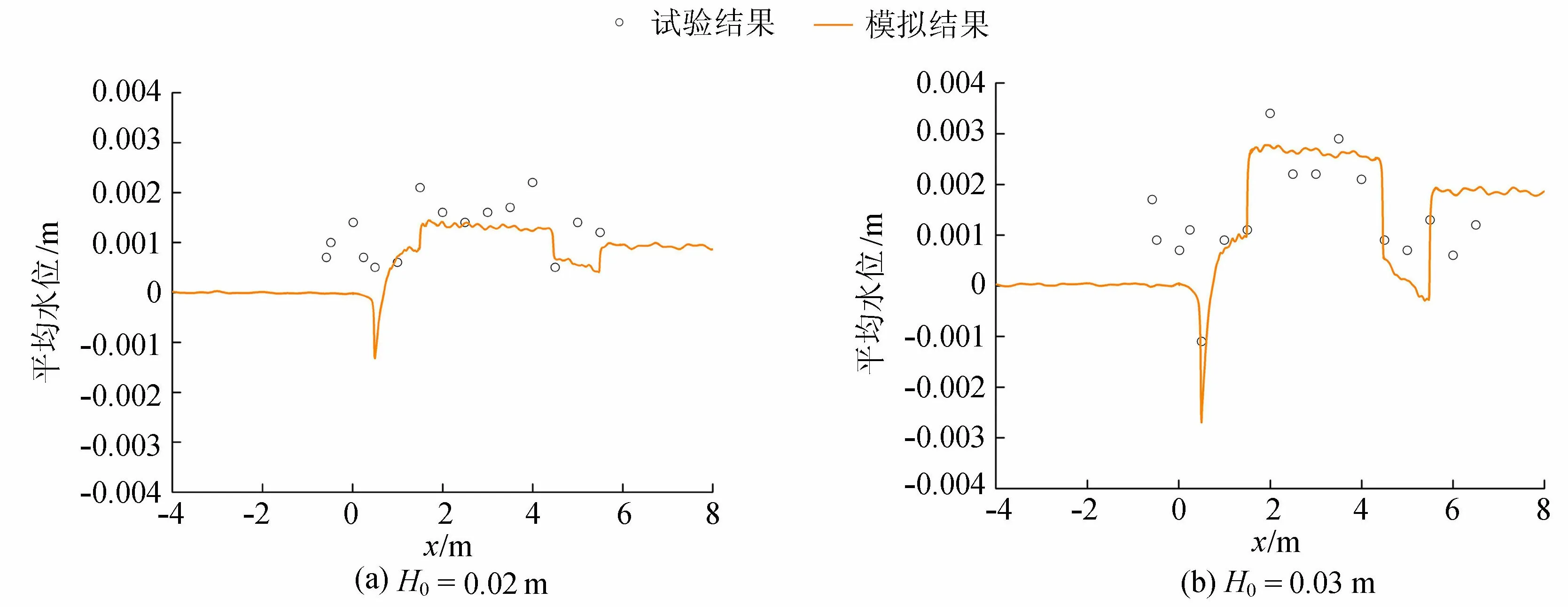
图5 平均水位试验结果和模拟结果对比
平均波高、平均水位的试验结果与模拟结果对比见图4和图5。图4和图5中平均波高曲线的数值模拟结果与试验结果基本吻合,平均水位曲线的数值模拟结果与试验结果稍有偏差,但是趋势符合。可见用本文模型研究陡峭礁坪地形上波浪的传播规律是可行的。
3 波浪在陡峭礁坪上传播变形的模拟
为了解陡峭礁坪地形对波浪传播的影响情况,用本文模型对不同情况下波浪在礁坪上传播特性进行了模拟和分析,包括不同入射波高H0、不同周期T、不同礁坪上水深hr情况下波浪的衰减情况。礁坪模型剖面示意图如图6所示,模型全长30 m,坡比i=1∶1。主要波浪要素:水深d=0.50 m、周期T=0.8 s、0.9 s、1.0 s,入射波高H0=0.02 m、0.04 m、0.06 m,礁坪上水深hr=0 m、0.02 m、0.04 m。破碎控制项H/h1=0.8(H为沿程平均波高,h1为波浪行进到某点的静水深)。

图6 礁坪上传播特性试验模型剖面示意图(单位:m)
3.1 不同入射波高下的传播特性
在坡比i=1∶1、水深d=0.50 m、周期T=0.8 s的情况下,不同入射波高的波浪在陡峭礁坪地形上传播时,其相对平均波高H/H0沿程分布的模拟结果如图7所示(图中L0为入射波长)。
从图7可见,当波浪传播至礁坪位置时,由于水深急剧变浅,波浪发生反射和破碎等现象,从而礁坪上的波高迅速降低。当x=2L0时,礁坪上的平均波高约降低为入射波高的1/4;而当x=4L0时,礁坪上的平均波高可降低为入射波高的20%以下。
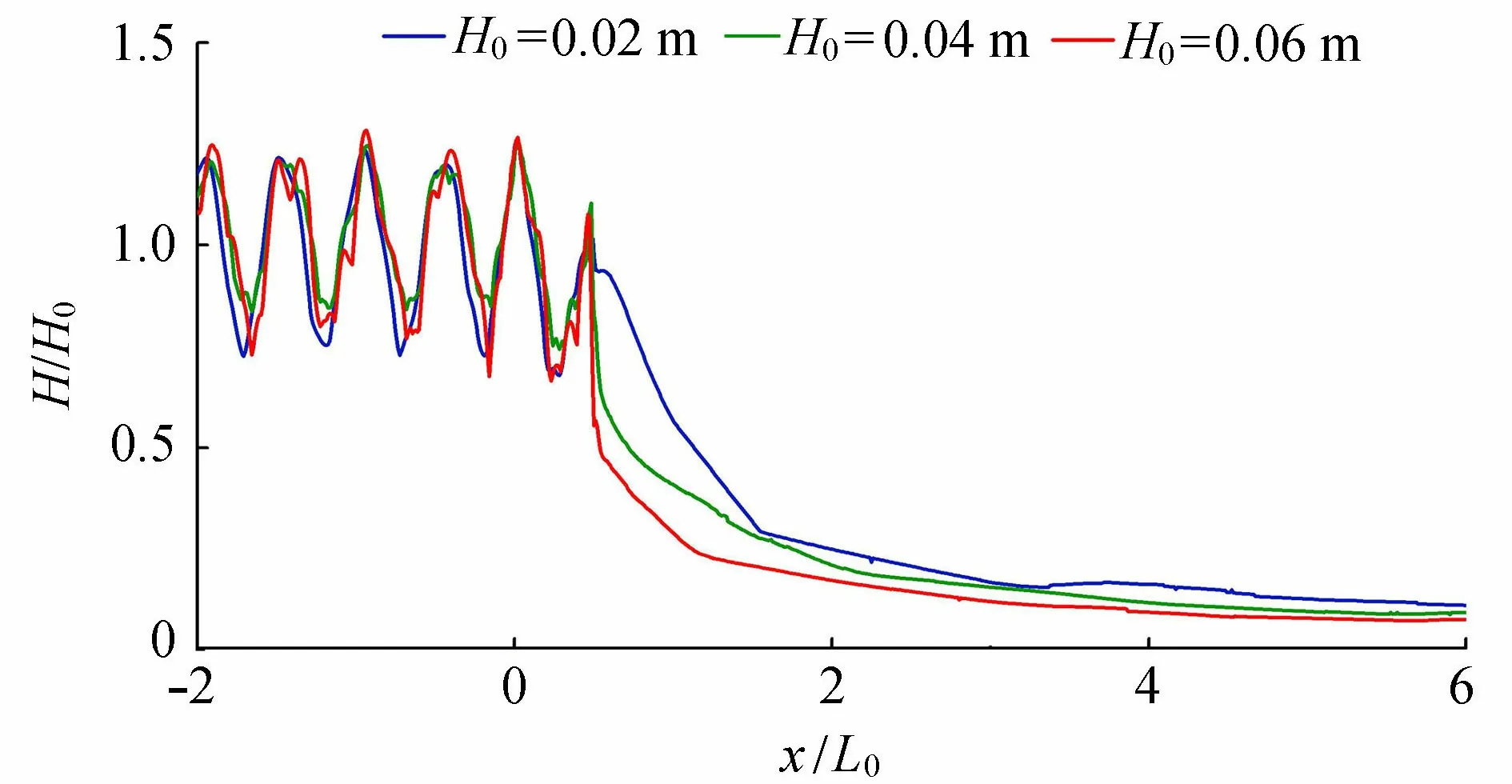
图7 不同入射波高下相对平均波高沿程变化
3.2 不同礁坪上水深时的传播特性
在坡比i=1∶1、水深d=0.50 m、入射波高H0=0.02 m、周期T=0.8 s的情况下,不同礁坪上水深时波浪传播的相对平均波高H/H0沿程分布的模拟结果如图8所示。
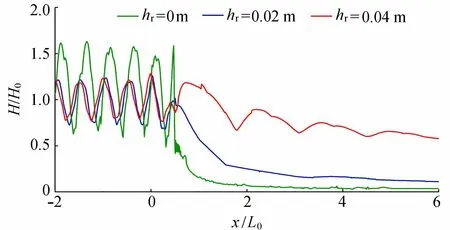
图8 不同礁坪上水深时相对平均波高沿程变化
从图8可见,当波浪传播至礁坪位置时,波浪发生浅水变形现象,礁坪上的波高急剧降低,发生破碎。对于hr=0 m、0.02 m的情况,当x=2L0时,礁坪上的平均波高约降低为入射波高的1/4;而当x=4L0时,礁坪上的平均波高可降低为入射波高的20%以下。但对于hr=0.04 m的情况,礁坪上的平均波高仅仅降低为入射波高的1/2,但呈现逐渐下降的趋势。
3.3 不同周期下的传播特性
在入射波高H0=0.02 m、坡比i=1∶1、水深d=0.50 m、礁坪上水深hr=0.02 m的情况下,不同周期的波浪传播相对平均波高H/H0沿程分布的模拟结果如图9所示。
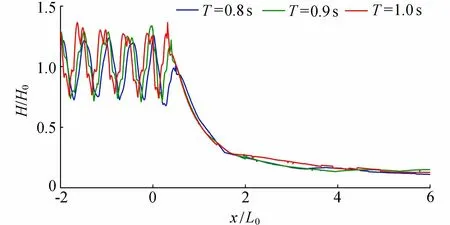
图9 不同周期下相对平均波高沿程变化
从图9可见,当波浪传播至礁坪位置时,由于水深急剧变浅,波浪发生反射和破碎等现象,从而礁坪上的波高急剧降低。当x=2L0时,礁坪上的平均波高约降低为入射波高的30%;而当x=4L0时,礁坪上的平均波高可降低为入射波高的20%以下。
4 结 语
本文基于Funwave-TVD波浪数值模型,对波浪在陡峭礁坪上的传播变形和破碎规律进行了数值模拟,结果表明,对于深水情况下的陡峭礁坪地形,波浪离开礁坪坡脚的水平距离为4L0及更远时,礁坪上的平均波高可降低为入射波高的20%以下,在此位置及其以后设置建筑物较为理想。
[1] 赵子丹,张庆河,刘海青.波浪在珊瑚礁及台阶式地形上的传播[J].海洋通报,1995,14(4):1-10.(ZHAO Zidan,ZHANG Qinghe,LIU Haiqing.Wave transformation on coral reefs and submerged steps[J].Marine Science Bullftin,1995,14(4):1-10.(in Chinese))
[2] 黎满球,朱良生,隋世峰.珊瑚礁坪波浪的衰减特性分析[J].海洋工程,2003,21(2):71-75.(LI Manqiu,ZHU Liangsheng,SUI Shifeng.Characteristics of wave attenuation on the coral reef[J].The Ocean Engineering,2003,21(2):71-75.(in Chinese))
[3] ROEBER V,CHEUNG K F.Boussinesq-type model for energetic breaking waves in fringing reef environments[J].Coastal Engineering,2012,70 (4):1-20.
[4] 梅弢,高峰.波浪在珊瑚礁坪上传播的水槽试验研究[J].水道港口,2013,34(1):13-18.(MEI Tao,GAO Feng.Flume experiment research on law of wave propagation on reef flat[J].Journal of Waterway and Harbor,2013,34(1):13-18.(in Chinese))
[5] 柳淑学,刘宁,李金宣,等.波浪在珊瑚礁地形上破碎特性试验研究[J].海洋工程,2015,33(2):42-49.(LIU Shuxue,LIU Ning,LI Jinxuan,et al.Experimental researches on propagation characteristics on reefs terrain[J].The Ocean Engineering,2015,33(2):42-49.(in Chinese))[6] 郑金海,余豪丰,陶爱峰,等.波浪布拉格共振研究进展[J].水利水电科技进展,2016,36(3):83-87.(ZHENG Jinhai,YU Haofeng,TAO Aifeng,et al.Research progress in wave Bragg resonance[J].Advances in Science and Technology of Water Resources,2016,36(3):83-87.(in Chinese))
[7] 李炎保,孙晓彦.波浪在陡坡上的传播变形[J].海洋与湖沼,1998,29(3):241-246.(LI Yanbao,SUN Xiaoyan.Wave propagation and transformation on steep slope[J].Oceanlogia et Limnologia Sinica,1998,29(3):241-246.(in Chinese))
[8] 刘海青,赵子丹,张庆河.台阶地形上波浪运动的数值研究[J].水利学报,1998,10(2):8-13.(LIU Haiqing,ZHAO Zidan,ZHANG Qinghe.Numerical model for transformation of wave passing over a step[J].Journal of Hydraulic Engineering,1998,10(2):8-13.(in Chinese))
[9] DOUILLET P,OUILLON S,CORDIER E.A numerical model for fine suspended sediment transport in the southwest lagoon of New Caledonia[J].Coral Reefs,2001,20(4):361-372.
[10] YAO Y,HUANG Z,MONISMITH S G,et al.1DH Boussinesq modeling of wave transformation over fringing reefs[J].Ocean Engineering,2012,47(10):30-42.
[11] 祁国军,袁新明.斜坡堤栅栏板护面波浪爬高数值模拟[J].水利水电科技进展,2012,32(5):16-19.(QI Guojun,YUAN Xinming.Numerical simulation of wave run-up on fence panels of sloping dikes[J].Advances in Science and Technology of Water Resources,2012,32(5):16-19.(in Chinese))[12] 房克照,刘忠波.潜礁上孤立波传播的数值模拟[J].哈尔滨工程大学报,2014,35(3):295-300.(FANG Kezhao,LIU Zhongbo.Simulation of solitary wave transformation over reef profile[J].Journal of Harbin Engineering University,2014,35(3):295-300.(in Chinese))
[13] KIRBY J T,WEI G,CHEN Q.Funwave 1.0:fully nonlinear Boussinesq wave model documentation and users manual[Z].Newark,Delaware,USA:University of Delaware,1998.
[14] SHI F Y,JAMES T,KIRBY J T.Fully nonlinear boussinesq wave model with TVD solver[Z].Newark,Delaware,USA:University of Delaware,2012.
[15] CHEN Q.Fully nonlinear Boussinesq-type equations for waves and currents over porous beds[J].Journal of Engineering Mechanics,2006,132(2):220-230.
[16] KENNEDY A B,KIRBY J T,CHEN Q,et al.Boussinesq-Type equations with improved nonlinear performance[J].Wave Motion,2001,33(5):225-243.
[17] WEI G,KIRBY J T,JAMES T.et al.A fully nonlinear Boussinesq forsurface waves:part 1.highly nonlinear unsteady waves[J].Journal of Fluid Mechanics,1995,3(1):71-92.
[18] TONELLI M,PETTI M.Hybrid finite volume-finite difference scheme for 2DH improved Boussinesq equations[J].Coastal Engineering,2009,56(6):609-620.
[19] YAO Y,EDMOND Y M,HUANG Z H,et al.An experimental study of wave-induced set-up over a horizontal reef with an idealized ridge[C]//28th International Conference on Ocean,Offshore and Arctic Engineering.New York:ASME,2009:383-389.
Numerical modeling of wave propagation and deformation on steep reef based on Boussinesq equation//
HUANG Yingli, WANG Guoyu, FANG Kezhao, CHEN Ge
(StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)
In order to explore the feasibility of simulating wave propagation and deformation on a steep reef with the Funwave-TVD wave model based on the second-order fully nonlinear Boussinesq equation, using feasibility validation with the data form experiments and published papers, the wave propagation and deformation process on the steel reef was simulated with the model, and the wave propagation characteristics on the reef were analyzed with different wave elements and water depths. The numerical results show that when the ratio of the wave height to the water depth exceeds a certain value, the wave breaks and the wave height decreases quickly. In deep water conditions, the average wave height on the steep reef decreases to a stable value when the wave moves away from the slope toe of the reef to a distance four times the incident wavelength or further.
wave propagation; propagation and deformation; steep reef; Boussinesq equation; Funwave-TVD
黄英丽(1991—),女,硕士研究生,主要从事海岸动力学研究。E-mail:844632149@qq.com
10.3880/j.issn.1006-7647.2017.01.007
TV139.2
A
1006-7647(2017)01-0038-05
2015-12-25 编辑:熊水斌)

