航空航天业创新能力的动态演进与空间格局
——基于突变级数与聚类分析方法
郭鸿雁
(1.郑州航空工业管理学院,河南 郑州 450046;2.航空经济发展河南省协同创新中心,河南 郑州 450046)
航空航天业创新能力的动态演进与空间格局
——基于突变级数与聚类分析方法
郭鸿雁1,2
(1.郑州航空工业管理学院,河南 郑州 450046;2.航空经济发展河南省协同创新中心,河南 郑州 450046)
文章采用突变级数法构建航空航天业创新能力的指标体系与评价模型,运用2000~2014年航空、航天器及设备制造业专利数据,结合聚类分析方法,对我国航空航天业创新能力的动态演进与空间格局进行分析。结果表明:航空航天业创新能力在2000~2014年间经历三个阶段跃迁:较低水平阶段(2000~2007年)、中等水平阶段(2008~2011年)、较高水平阶段(2012~2014年),两次突变时点分别对应2008年与2012年;当前航空航天业创新能力在空间格局上呈现出显著的马太效应以及阶梯状分布特征,该特征与产业资源禀赋因素密切相关。
航空航天业;创新能力;动态演进;空间格局
一、引 言
当前,新一代信息技术与制造业深度融合,正在引发全球范围内影响深远的产业革命。各国都在加大科技创新力度,推动3D打印、移动互联网、云计算、大数据等领域取得新突破。2015年5月,国务院印发《中国制造2025》行动纲领,明确提出“以促进制造业创新发展为主题”,“以加快新一代信息技术与制造业深度融合为主线”,“培育有中国特色的制造文化,实现制造业由大变强的历史跨越”。其中,特别强调“坚持把创新摆在制造业发展全局的核心位置”,并制定创新能力指标:“规模以上制造业每亿元主营业务收入有效发明专利数”到2025年达到1.10。
2015年10月,党的十八届五中全会审议通过《中共中央关于制定国民经济和社会发展第十三个五年规划的建议》,进一步明确提出“创新是引领发展的第一动力”。航空航天业是以航空、航天器作为主要研制、生产、维修和经营对象的国家战略性高技术产业,具有产业链长、辐射面宽、技术扩散率高、拉动效应强等鲜明特点,对科学技术进步和国民经济发展具有巨大带动作用。
伴随工业化的不断深化,航空航天业的技术创新能力对于产业发展的关键性作用日益突出。目前,我国航空航天业技术创新动力不足,产业结构升级与优化较多依赖外商投资与技术引进,在世界航空航天科技和工业发展速度不断加快的背景下,研究航空航天业技术尤其是关键技术创新,对于促进航空航天业技术进步、推动航空航天业向自主创新转型升级、打造有中国特色的航空制造文化具有重要的现实意义。
本文采用突变级数法构建航空航天业创新能力的指标体系与评价模型,运用2000~2014年航空、航天器及设备制造业专利数据,结合聚类分析方法,对我国航空航天业创新能力的动态演进与空间格局进行分析。
二、基于突变级数的航空航天业创新能力的动态演进
突变理论是研究客观世界非连续性突然变化现象的一门新兴学科,由法国数学家勒内·托姆(René Thom)于1972年在其专著《结构稳定性和形态发生学》中首次系统提出。在该书中,托姆将系统内部状态的整体性“突跃”称为突变,用以描述自然界和人类社会活动中的跳跃式转变、不连续过程和突发性质变。由于该理论突破了长期以来微积分只能解决光滑连续变化问题的局限,因此问世后备受关注,被誉为“牛顿和莱布尼茨发明微积分三百年以来数学上最大的革命”,托姆也由此荣获国际数学界的最高奖——菲尔兹奖。
目前关于航空航天业创新能力的理论研究中,较多采用了定性分析或以审计评价(杨德林、刘方、杨俊波,2004[1])、结构模型(张政治、谢毅梅、张文强,2011[2];刘光智,2012[3])等为主要手段的定量分析,而将突变理论运用其中,则鲜有类似思路和方法。运用突变理论,结合专利数据研究航空航天业创新能力的动态演进,主要基于以下考虑:首先,创新能力的状态演进是从量变到质变的过程,当创新能力达到某一临界点时将会引起状态突变,因此采用突变理论进行分析恰如其分;再者,专利是测度技术研发绩效的核心指标,航空航天业的专利数据代表了该产业的整体创新水平。
(一)突变级数评价法概述
突变级数评价法是将突变理论与模糊数学相结合,通过突变模糊隶属函数对评价目标进行分析的综合评价技术。由于该方法没有对评价指标采用权重,而是考虑各指标的相对重要性,从而在减少主观性的同时不失科学性和合理性;同时,该方法计算过程简易准确,因此其应用范围较为广泛。
突变级数评价法的操作步骤主要包括:
1.建立评价指标体系
根据评价目标,将待评价对象进行逐层分解,形成由若干评价指标组成的多层系统,并排列成倒立树状层次结构。其中,指标分解要求直至出现能够量化的指标为止,同级指标须以重要程度为序进行排列。
2.确定评价体系各层次突变系统模型及其状态变量临界值归一化算式
将评价体系各层次评价指标视为该层次的控制变量,根据控制变量个数选定相应的突变系统类型。具体来说,单一控制变量选择折叠突变系统模型,两控制变量选择尖点突变系统模型,三控制变量选择燕尾突变系统模型,四控制变量选择蝴蝶突变系统模型。
对于不同层次的突变系统模型,运用该势函数的一阶和二阶条件求解该模型的分歧点集方程。当控制变量满足分歧方程时,系统状态将发生突变。不同突变系统类型的势函数及其状态变量临界值归一化算式见表1。

表1 不同突变系统模型及其归一化算式
3.在对底层数据正规化处理基础上逐层计算状态变量的归一化值
为了排除量纲及数据取值范围对分析结论的影响,首先对底层原始数据剔除量纲,即采取正规化处理。正规化转换公式如下:
zij= xij/max(xij)
(1)
式(1)中,xij代表底层第j个指标的第i个原始数据,max(xij)代表底层第j个指标的最大原始数据,zij代表正规化转换后的数据。
在对底层数据进行正规化处理后,根据各层次突变系统模型及其状态变量临界值归一化算式,逐层计算各层次状态变量的归一化值。归一化值的取值原则是:当该层次诸控制变量间属于互补关系时,其状态变量归一化值的综合值采用算术平均值计算;当该层次诸控制变量间不存在互补关系时,其状态变量归一化值的综合值按照“大中取小”原则计算。
4.根据顶层状态变量的归一化综合值进行综合评价
根据各层次突变系统模型及其状态变量临界值归一化算式,通过逐层计算,最终得到顶层状态变量的归一化综合值。以此为评判指标,进而对待评价对象的突变特征进行综合评价。在评价过程中,多采用统计分析方法,例如聚类分析,即以顶层状态变量的归一化综合值为指标,对待评价对象的演变路径进行分段,如果相邻演进阶段之间存在统计上的显著差异,则可断定上述两阶段之间发生了状态突变。
(二)航空航天业创新能力的突变级数评价模型
1.指标选择
专利是测度技术研发绩效的核心指标,航空航天业的专利数据代表了该产业的整体创新水平。根据专利研究的国际惯例,结合指标数据的全面性、科学性与可得性,本文从专利数量与专利质量两个维度,分别选取“航空、航天器及设备制造业专利申请数”“航空、航天器及设备制造业发明专利占比”作为衡量航空航天业创新能力的分析指标。
2.模型构建
根据突变级数评价法的工作思想与研究思路,结合上述指标选择,构建航空航天业创新能力的突变级数评价模型,如图1所示。
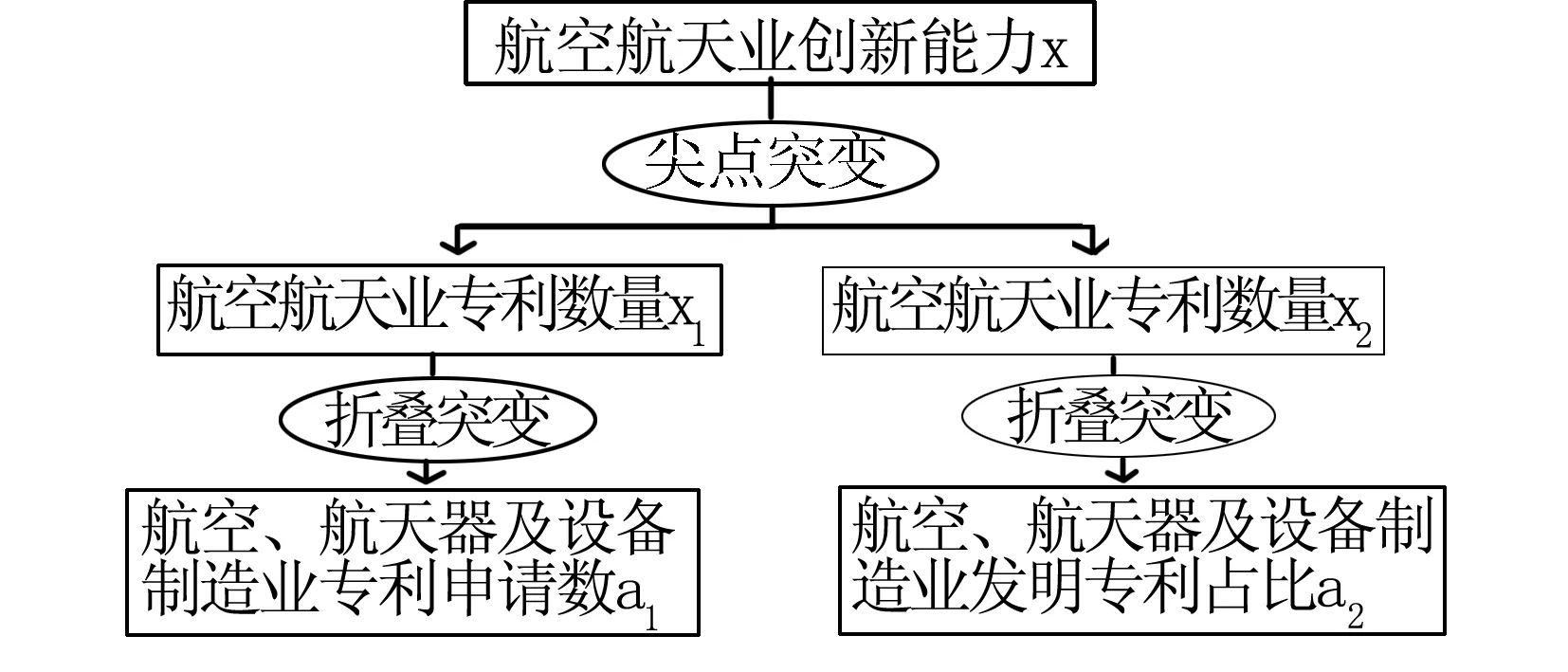
图1 航空航天业创新能力的突变级数评价模型
在图1中,状态变量“航空航天业创新能力x”通过两个控制变量——“航空航天业专利数量x1”“航空航天业专利质量x2”予以反映,故属于尖点突变系统模型;“航空航天业专利数量x1”“航空航天业专利质量x2”分别通过单一控制变量“航空、航天器及设备制造业专利申请数a1”“航空、航天器及设备制造业发明专利占比a2”予以反映,故均属于折叠突变系统模型。需要说明的是,控制变量“航空航天业专利数量x1”“航空航天业专利质量x2”的排序,表明航空航天业在创新转型初期,创新数量较创新质量更为重要。
(三)数据结构与描述
1.数据结构
根据航空航天业创新能力的突变级数评价模型,原始数据取自国家统计局、科学技术部编写的《中国科技统计年鉴》(2006~2015)[4],选用数据包括“航空、航天器及设备制造业专利申请数”“航空、航天器及设备制造业发明专利”,时间跨度为2000~2014年。
根据研究需要,“航空、航天器及设备制造业发明专利占比”由“航空、航天器及设备制造业发明专利”与“航空、航天器及设备制造业专利申请数”计算比值得到。航空、航天器及设备制造业专利原始数据(2000~2014)见表2。
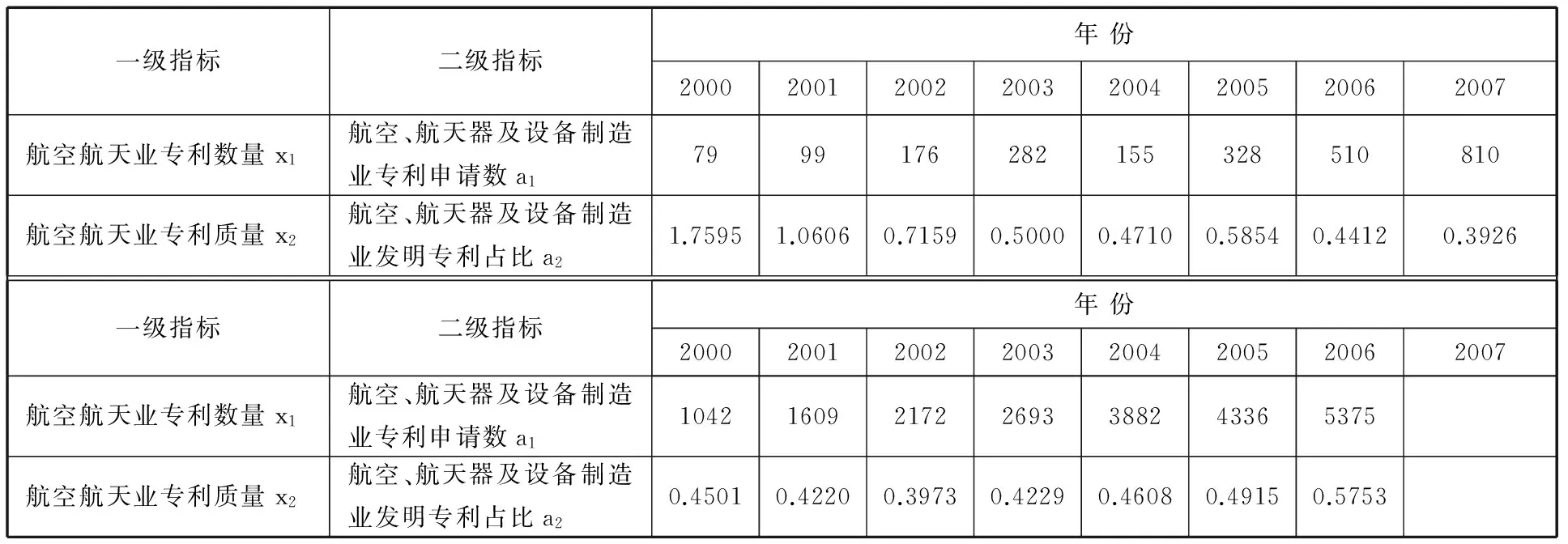
表2 航空、航天器及设备制造业专利原始数据(2000~2014)
数据来源:国家统计局、科学技术部编,《中国科技统计年鉴》(2006~2015),中国统计出版社.
2.数据描述
(1)航空、航天器及设备制造业专利申请数
航空、航天器及设备制造业专利申请数(2000~2014)的变化趋势如图2。由图可见,剔除个别年份的数据波动,航空、航天器及设备制造业专利申请数在2000~2007年间处于低水平缓慢上升阶段,其取值均在1000单位以下;而2008年后则大幅上扬,目前取值已突破5000单位。
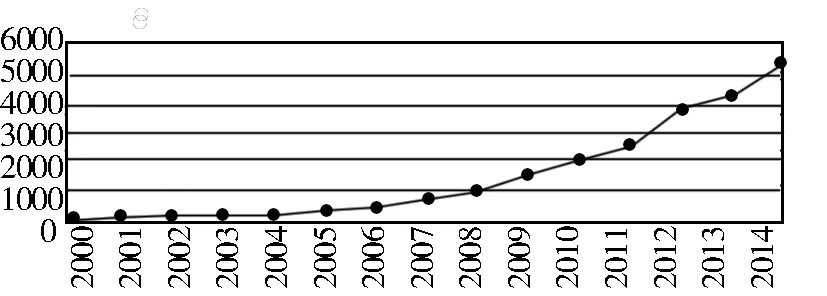
图2 航空、航天器及设备制造业专利申请数(2000~2014)
(2)航空、航天器及设备制造业发明专利占比
航空、航天器及设备制造业发明专利占比(2000~2014)的变化趋势如图3。由图可见,剔除个别年份的数据波动,航空、航天器及设备制造业发明专利占比在2000~2007年间处于快速下降阶段,其取值一度跌至40%以下;而2008年后则进入平稳上升阶段,其取值接近50%;值得一提的是2014年,取值近60%。
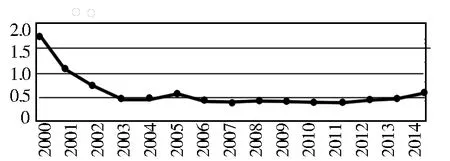
图3 航空、航天器及设备制造业发明专利占比(2000~2014)
(四)分析过程与结论
1.数据处理
根据航空航天业创新能力的突变级数评价模型,按照突变级数评价法的操作步骤,在对底层数据进行正规化处理基础上,根据各层次突变系统模型及其状态变量临界值归一化算式,通过逐层计算,最终得到顶层状态变量,即一级指标的归一化值及其综合值,见表3。
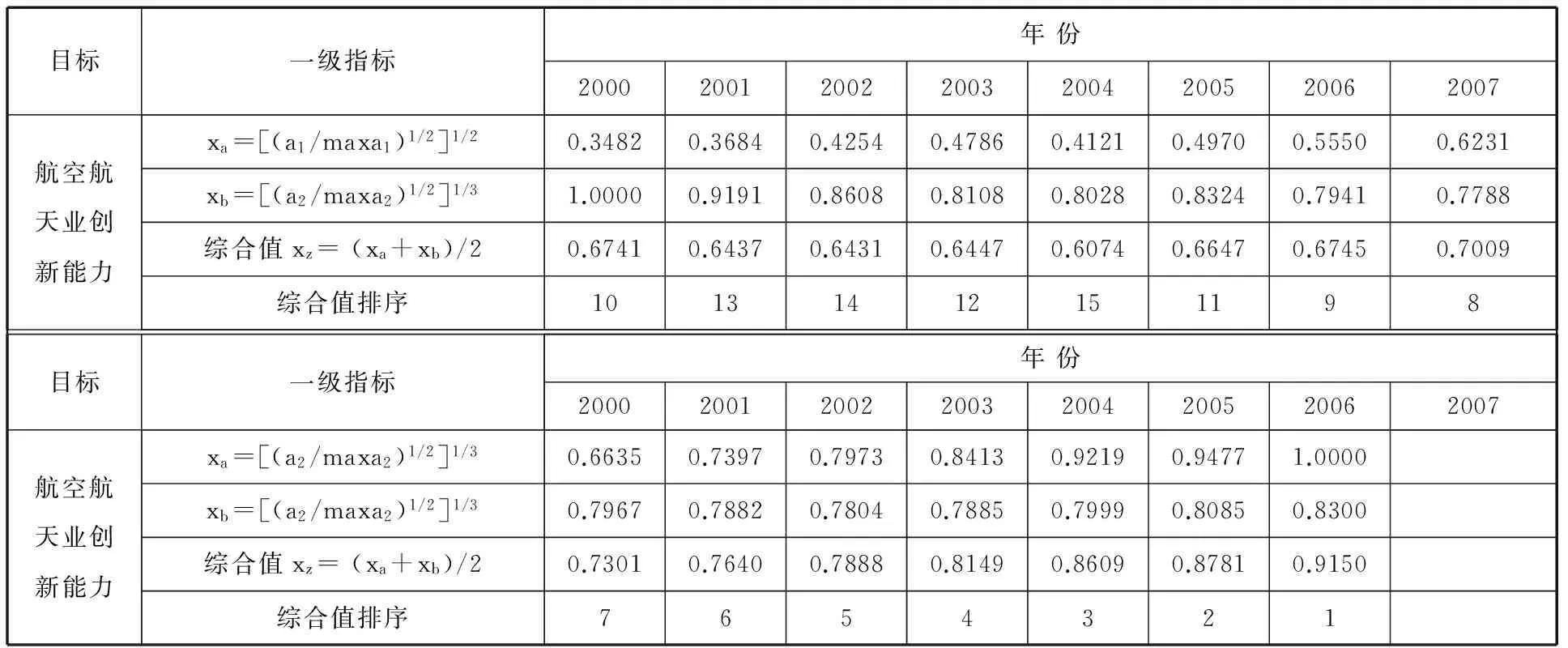
表3 航空航天业创新能力一级指标的归一化值及其综合值
在表3中,计算得到的一级指标的归一化综合值xz,即为衡量航空航天业创新能力的综合指标。按照综合值xz由大到小进行排序,年份依次为:2014、2013、2012、2011、2010、2009、2008、2007、2006、2000、2005、2003、2001、2002、2004。不难看出,航空航天业创新能力自2005年以来进入稳步上升过程, 而在2004年以前则处于低水平波动状态。
2.结合聚类方法的进一步分析
在表3基础上,通过绘制综合值xz的变化趋势,能够更好地展现出航空航天业创新能力的动态演进历程,如图4所示。据图判断,航空航天业创新能力在2000~2014年间大致经历了三个阶段的跃迁:第一阶段在2000~2007年,综合值xz基本处于0.7以下,处于较低水平阶段;第二阶段在2008~2011年,综合值xz大致处于0.7~0.8,处于中等水平阶段;第三阶段在2012年后,综合值xz接近0.9左右,处于较高水平阶段。
进一步利用统计分析方法对上述结论进行验证。令聚类数为3,对综合值xz按所属年份进行K-均值聚类,结论见表4。
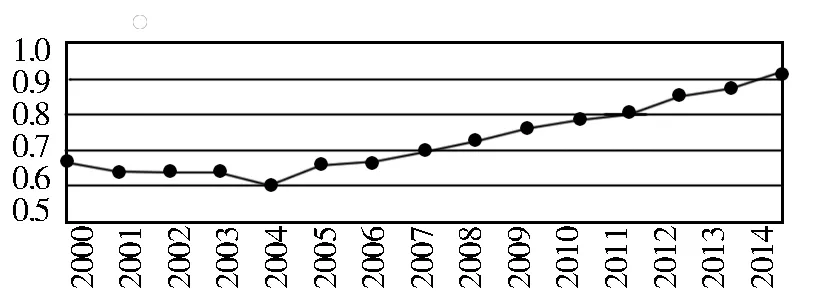
图4 航空航天业创新能力的动态演进(2000~2014)
表4 航空航天业创新能力演进的K-均值聚类分析
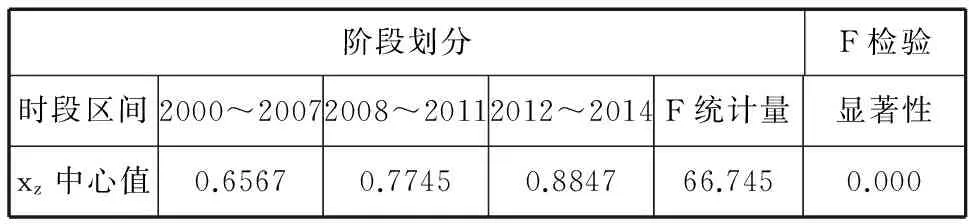
阶段划分F检验时段区间2000~20072008~20112012~2014F统计量显著性xz中心值0.65670.77450.884766.7450.000
从分析结论看,K-均值聚类将航空航天业创新能力的动态演进历程划分为2000~2007年、2008~2011年、2012~2014年三个阶段,各阶段xz中心值分别为0.6567、0.7745、0.8847,且方差分析的F统计量通过显著性检验。为此,K-均值聚类结论很好地验证并支持了上述经验判断。
3.分析结论
基于以上分析不难得到,航空航天业创新能力在2000~2014年间经历三个阶段跃迁:较低水平阶段(2000~2007年)、中等水平阶段(2008~2011年)、较高水平阶段(2012~2014年),期间历经两次突变,时点分别对应2008年和2012年。在这两个时点上,航空、航天器及设备制造业的专利申请数和发明专利占比均出现了显著变化,二者共同作用,导致相关状态变量突破相应突变系统模型状态变量的临界值,进而发生突跳,从而形成了不同阶段的跃迁。
值得注意的是,突变的发生往往以顶层状态变量归一化值的综合值显著变化为特征,通常要求突变系统模型中各个控制变量均呈现出不断逼近并突破相应临界值的变动趋势。为此,仅有突变系统模型中部分或个别控制变量的显著变化,并不能形成突跳,进而产生突变。
三、基于聚类分析的航空航天业创新能力的空间格局
聚类分析起源于分类学,是一种常见的多元统计分析技术,主要致力于将研究对象区分为具有相对同质的不同群组。利用聚类分析方法,能够对航空航天业创新能力的区域分布特征进行分类研究,从而较好地把握其空间格局。
(一)数据结构与描述
1.数据结构
在前文分析基础上,结合航空航天业创新能力空间格局的研究需要,原始数据取自国家统计局、国家发展和改革委员会、科学技术部编《中国高技术产业统计年鉴》(2015)[5],选用数据包括“航空、航天器及设备制造业专利申请数”、“航空、航天器及设备制造业发明专利”,分析对象包括全国31个省市自治区,时点为2014年。
同前所述,“航空、航天器及设备制造业发明专利占比”由“航空、航天器及设备制造业发明专利”与“航空、航天器及设备制造业专利申请数”计算比值得到。全国31个省市自治区航空、航天器及设备制造业专利原始数据(2014)见表5。
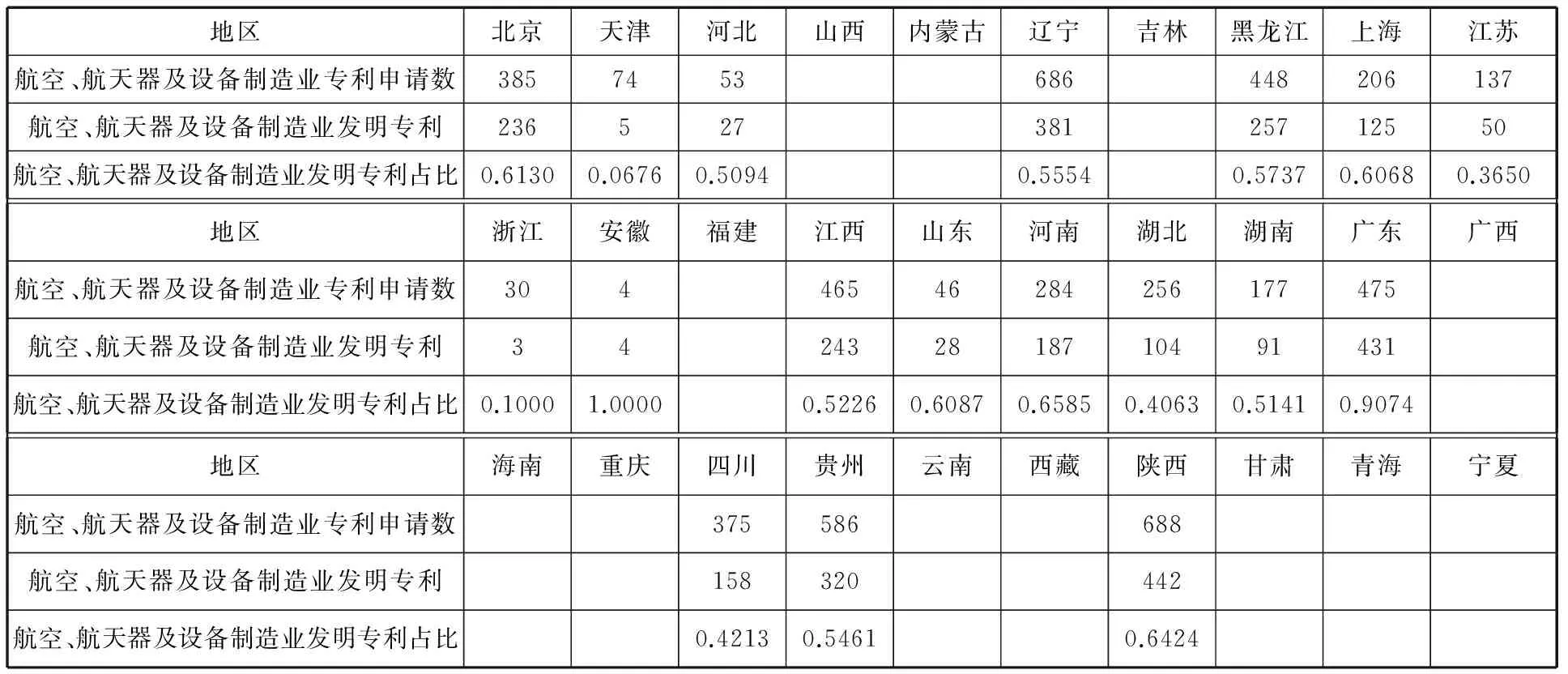
表5 全国31省市自治区航空、航天器及设备制造业专利原始数据(2014)
注:原始数据部分缺失.
数据来源:国家统计局、国家发展和改革委员会、科学技术部编,《中国高技术产业统计年鉴(2015)》,中国统计出版社,2015.
2.数据描述
根据表5数据,以“航空、航天器及设备制造业专利申请数”、“航空、航天器及设备制造业发明专利”为坐标轴,利用散点图绘出2014年全国31省市自治区航空、航天器及设备制造业的专利分布情况,从中能够大体得出航空航天业创新能力的空间格局特征,如图5所示。
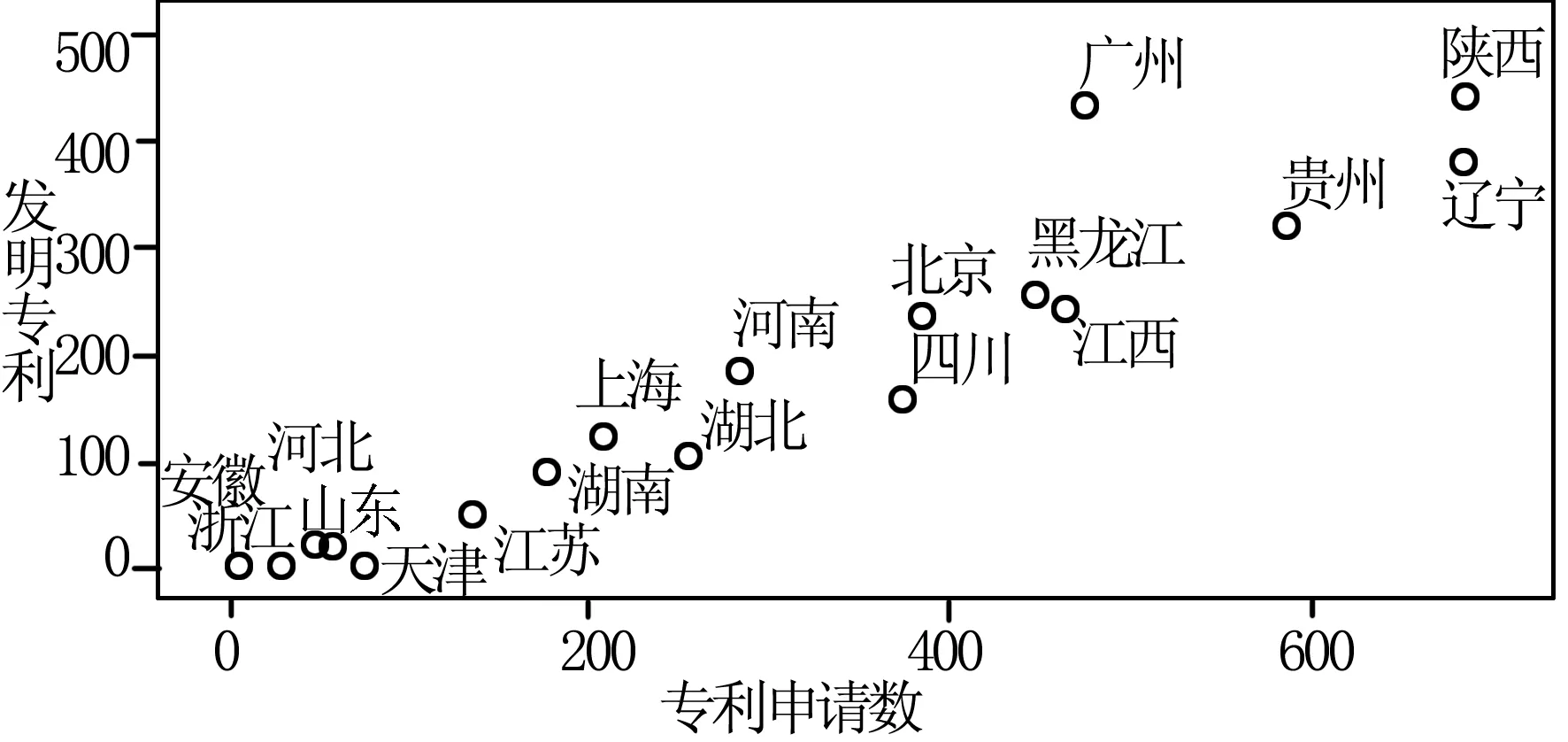
图5 航空航天业创新能力的空间格局(2014)
(二)分析过程与结论
1.分析过程
根据图5所示2014年全国31省市自治区航空、航天器及设备制造业的专利分布情况,当前我国航空航天业创新能力在空间分布上呈现出显著的马太效应,即“强者恒强、弱者恒弱”,在图形上即表现为相关散点整体呈现向右上方倾斜的变动趋势。以由强及弱为序,航空航天业创新能力的空间格局大体能够被区分为“强—次强—次弱—弱”等四种不同类型。其中,“强”类型主要体现在陕西、辽宁、贵州等航空航天工业发达地区;“弱”类型主要体现在安徽、浙江、河北、山东、天津等航空航天工业相对落后地区;其他地区则介于二者之间。
进一步分析,利用聚类分析方法对上述结论进行验证。令聚类数为4,对航空、航天器及设备制造业的专利申请数、发明专利及发明专利占比进行K-均值聚类,结论见表6。
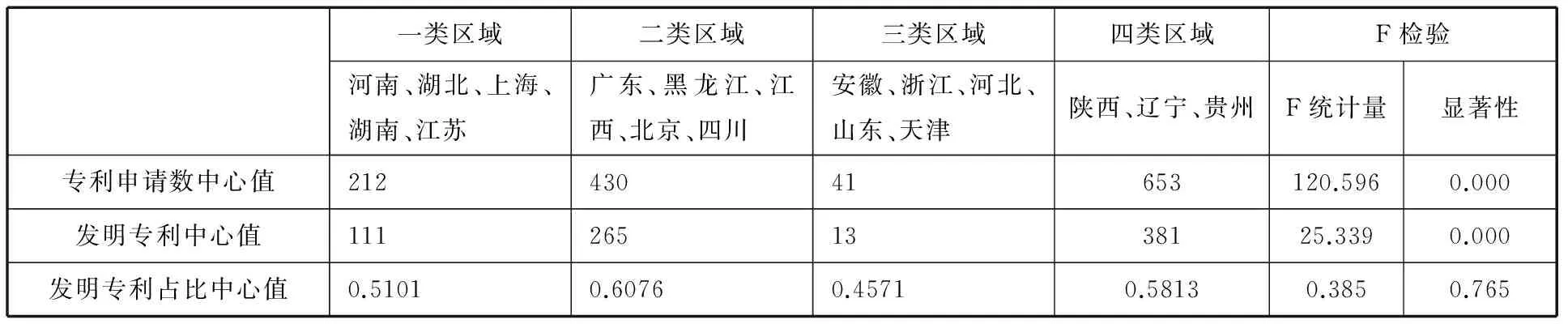
表6 航空航天业创新能力空间格局的K-均值聚类分析
从分析结论看,K-均值聚类将航空航天业创新能力的空间格局划分为四大类区域,第一类区域包括河南、湖北、上海、湖南、江苏,专利申请数、发明专利及发明专利占比的中心值分别为212、111、0.5101;第二类区域包括广东、黑龙江、江西、北京、四川,专利申请数、发明专利及发明专利占比的中心值分别为430、265、0.6076;第三类区域包括安徽、浙江、河北、山东、天津,专利申请数、发明专利及发明专利占比的中心值分别为41、13、0.4571;第四类区域包括陕西、辽宁、贵州,专利申请数、发明专利及发明专利占比的中心值分别为653、381、0.5813;此外,专利申请数以及发明专利的F统计量均通过显著性检验。因此,K-均值聚类结论很好地验证并支持了上述经验判断。
2.分析结论
基于以上分析不难得到,2014年我国航空航天业的创新能力在空间格局上呈现出显著的阶梯状分布特征,由强及弱分别对应于:强——陕西、辽宁、贵州等航空航天工业发达地区;次强——广东、黑龙江、江西、北京、四川等航空航天工业较发达地区;次弱——河南、湖北、上海、湖南、江苏等航空航天工业欠发达地区;弱——安徽、浙江、河北、山东、天津等航空航天工业相对落后地区。
深入剖析上述空间分布特征,与我国航空航天业发展的历史背景及其工业化进程密切相连。在此过程中需要强调指出的是,继20世纪50年代艰难起步之后,以“三线建设”为重要内容的全国工业布局战略性调整,在带动中西部地区经济繁荣的同时,更为航空航天业发展的产业部署与空间布局奠定了重要基础。
上述结论一方面印证了产业资源禀赋对于技术创新能力具有基础而深远的影响作用,提升航空航天业创新能力必须充分发挥资源禀赋优势;另一方面,该结论也从动态角度指明了未来航空航天业创新能力空间格局的发展方向与变动趋势,为优化航空航天产业科技资源布局提供了理论依据。
四、结 语
本文采用突变级数法构建航空航天业创新能力的指标体系与评价模型,运用2000~2014年航空、航天器及设备制造业的专利数据,结合聚类分析方法,对我国航空航天业创新能力的动态演进与空间格局进行分析。结果表明:航空航天业创新能力在2000~2014年间经历三个阶段跃迁:较低水平阶段(2000~2007年)、中等水平阶段(2008~2011年)、较高水平阶段(2012~2014年),期间历经两次突变,时点分别对应2008年和2012年;当前,航空航天业创新能力在空间格局上呈现出显著的马太效应以及阶梯状分布特征,这一特征与产业资源禀赋因素密切相关。
航空航天业是关系到国计民生的战略性高技术产业,提升其创新能力意义重大。在现有研究基础上,进一步剖析航空航天业创新能力的演化动力与机制、从动态角度深入探讨航空航天业创新能力的空间转换,将成为下一步研究的重点。
[1]杨德林,刘 方,杨俊波.中国航空工业企业技术创新能力评价[J].清华大学学报(哲学社会科学版),2004,(4):77-83.
[2]张政治,谢毅梅,张文强.我国航空航天产业创新能力提升路径分析[J].科技管理研究,2011,(5):7-10.
[3]刘光智.中国航空航天产业创新能力及其评价研究[D].合肥工业大学,2012.
[4]国家统计局,科学技术部.中国科技统计年鉴[M].北京:中国统计出版社,2006~2015.
[5]国家统计局,国家发展和改革委员会,科学技术部.中国高技术产业统计年鉴[M].北京:中国统计出版社,2015.
责任编校:陈 强,王彩红
Dynamic Evolution and Spatial Pattern of Innovation Capability of Aerospace Industry
GUO Hong-yan1,2
(1.Zhengzhou University of Aeronautics, Zhengzhou 450046,China;2.Collaborative Innovation Center for Aviation Economy Development ofHenan Province, Zhengzhou 450046, China)
Building the index system and evaluation model by the catastrophe progression method,and using the patent data of aviation, spacecraft and equipment manufacturing industry from 2000 to 2014, combined with the clustering analysis method, the paper analyses the dynamic evolution and spatial pattern of innovation ability of aerospace industry in China. The results show that the innovation ability of aerospace industry experienced three stages from 2000 to 2014: low level (from 2000 to 2007), medium level (from 2008 to 2011), higher level (from 2012 to 2014), and the two mutation time points are 2008 and 2012; The current spatial pattern of innovation ability of aerospace industry has remarkable characteristics of Matthew effect and ladder-like distribution, which are closely related to the industrial resource endowments.
aerospace industry; innovation capability; dynamic evolution; spatial pattern
2016-10-05
河南省高等学校哲学社会科学研究优秀学者资助项目(2016-YXXZ-09)
郭鸿雁,女,博士,教授,研究方向为产业经济、系统经济。
10.19327/j.cnki.zuaxb.1007-9734.2016.06.001
F426.5
A
1007-9734(2016)06-0001-07

