一类变量为梯形模糊数的线性规划
周喜华,贾洪信,邓胜岳,吴 瑶
(1.广东环境保护工程职业学院,广东 佛山 528216;2.湖南工业大学理学院,湖南 株洲 412007)
一类变量为梯形模糊数的线性规划
周喜华,贾洪信1,邓胜岳2,吴 瑶2
(1.广东环境保护工程职业学院,广东 佛山 528216;2.湖南工业大学理学院,湖南 株洲 412007)
针对变量为梯形模糊数的模糊线性规划问题,利用结构元方法定义了一种模糊数的排序准则,讨论了如何将变量是梯形模糊数的线性规划去模糊化,即将含有变量为梯形模糊数的模糊线性规划转化为经典模糊线性规划.同时,证明了该模型的最优解等价于经典的线性规划的最优解,再利用单纯形法求出最优解.并设计了求解该类模型的算法.通过算例验证了该方法的可行性和算法的有效性,从而为变量模糊的广义模糊线性规划问题的研究提供了新的方法.
模糊结构元;模糊线性规划;最优解
数学规划问题是人们在经济管理、工程技术和科学研等各个领域中常常遇到的问题,它所研究的是在众多的方案中如何找到最优的方案和什么样的方案是最优的方案.而最优化这一数学分支,则正是为了解决这些问题,提供了求解的方法和理论基础,是一门应用很广泛、实用性很强的学科.1965年,加利福尼亚大学扎德(Zadeh L.A[1])教授在《信息与控制》这一杂志上发表了一篇开创性的论文“Fuzzy Sets”,这标志着模糊数学的诞生.在实际管理问题的建模中,由于人类认知的局限性和环境的模糊性,因此,越来越多的学者和研究者投身于模糊数学理论及应用的研究,并取得了一些好的研究成果.如:Guu S M, Wu Y K[2]针对一种含有模糊约束的线性规划问题给出了一类求解的方法;Maleki H R, Tata M, Mashinchi M,et al[3]主要是研究了一类含有模糊决策变量的线性规划问题;Cadenas J M, Verdegay J L[4]主要研究了目标函数系数为模糊数的多目标模糊线性规划问题;曾庆宁[5]提出了一类模糊系数规划的定义,同时给出了求其模糊最优解的方案. Zimmermann[6]第一个提出了模糊线性规划的算法,后续各种各样的模糊规划的形式和求解算法被许多学者提出.Fang等人针对一种含有模糊系数的规划问题,提出了将这类问题转化成为能够用割平面法处理的线性半无限规划问题,他们求解这种类型的模糊线性规划问题的思想,全部是通过用各不相同的方法将其转化成为经典的线性规划求解的.考虑到寻优问题的多样性和复杂性,最近几年来许多学者提出了一些新的寻优算法,比如人工神经网络、禁忌搜索、模拟退火等.从几何上来说,线性规划的算法研究大致可以分为三种类型:第一类是单纯形类算法,即沿着可行域的边界按一定的旋转规则,从一个顶点(基本可行解)移至另一个更优的顶点;第二类是外点算法[6-7],即迭代点从可行域的外部收敛至原问题的最优解;第三类是内点算法[6,8],即迭代的路径是在可行域的内部进行的.1976年,R.Jain在解决模糊决策问题中,首次提出了一种排序方法之后,许多的研究工作者接踵提出很多的排序方法,其中涉及的排序指标的有40多种.虽然排序指标之间看起来有很大的不同,但它们大致可以分为三类[9]:一是将排序的每个模糊量都转化成实数,进而利用实数的自然序关系推导出模糊量的序关系;二是先行通过的所有的模糊量形成一个参考集,然后把参考集以每一个模糊量进行比较,从而确定模糊量之间的序关系;三是对模糊量的模糊关系进行构造,然后通过该模糊关系实现模糊量之间的两两比较.
本文主要针对于一类实际管理优化问题中变量为梯形模糊数的线性规划模型的研究,该类模型的求解难点在于模糊数的排序及其最优解存在的条件.本文利用模糊结构元理论[10-12],证明了变量为梯形模糊数的线性规划问题等价于线性规划问题,再设计算法得到了该类问题的最优解.避免了运用模糊λ截集理论将变量为模糊数的线性规划问题转化为多目标问题,简化了运算,从而为解决变量为梯形模糊数的线性规划问题提供了新途径.
1 模糊数的基础理论与模糊结构元的理论及其性质
1.1 模糊数的基础理论
经典集A可以由特征函数χA(x)唯一确定,即映射

确定了X上的经典子集A.χA(x)表明x对A的隶属程度,不过仅有两种状态:一个元素x要么属于A,要么不属于A.
定义1[9,13]设U是论域,称映射




Note:其中,NC(R)表示R上全体有界闭模糊数的集合.
由定义2知,模糊集的λ-截集Aλ是一个经典集,由隶属度不小于λ的成员构成.它的特征函数为


2)若λ≤μ,则Aλ⊇Aμ;
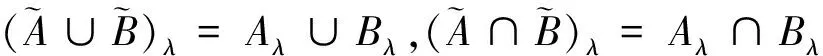



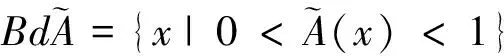


1.2 模糊结构元及其性质
定义4[10]设E为实数域R上的模糊集,隶属函数记为E(x),x∈R.如果E(x)满足下述性质:1)E(x)=1x>1;2)在区间[-1,0)上E(x)是单增右连续函数,在区间(0,1]上是单降左连续函数;3)当x<-1时,E(x)=0,则称E为R上的模糊结构元.
定义5[14]若模糊结构元E满足:1)∀x∈(-1,1),E(x)>0;2)E(x)连续,且在[-1,0)上严格单增,在(0,1]上严格单降,则称E为正则的;若E(-x)=E(x),称E为对称的.
1.3 梯形模糊数的结构元表示及其性质
引理2[15]设E是R上的任意模糊结构元,具有隶属函数E(x),f(x)是[-1,1]上单调有界函数,则f(E)是R上有界闭模糊数,其隶属函数为E(f-1(x)),这里E(f-1(x))是f(x)关于变量x和y的轮换对称函数(若f(x)是连续严格单调的,则E(f-1(x))是f(x)的反函数);反之,对于给定的正则模糊结构元E和任意的有界闭模糊数A,总存在一个[-1,1]上的单调有界函数f,使得A=f(E),称模糊数A是由模糊结构元E生成的.
设模糊集E具有隶属函数
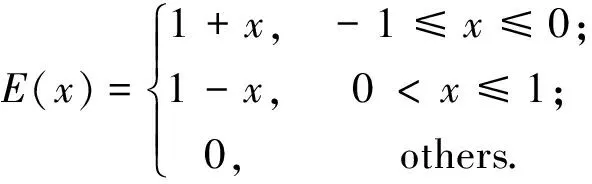
称其为三角结构元.
对于任意一个梯形模糊数
A=(a,b,c,d)(a≤b≤c≤d)也可以由三角结构元E生成,只要取[-1,1]上的分段单调有界集值函数

(1)
则同样有A=f(E)
其隶属函数[16]
定义6[15]设有界模糊数A的结构元表示A=f(E),其中E为某确定的模糊结构元,f为[-1,1]上的单调函数,记
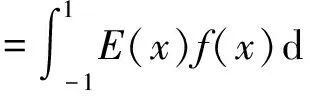
(2)
称‖A‖为有界模糊数A的结构元加权特征数,简称为A的特征数.
当模糊数A=(a,b,c,d)(a≤b≤c≤d)为梯形模糊数时,其的特征数为

(3)
如果A=(a,a,a,a)=a,即A为明确的实数时,则‖a‖=a.
定义7[11,15]设A1,A2∈Nc(R)其结构元表达形式分别为At∈ft(E),i=1,2其中E是给定的某个正则模糊结构元,隶属函数为E(x),f1,f2是[-1,1]上的同序单调函数,则由下式A1≤A2⟺‖A1‖≤‖A2‖称“≤”为模糊数的结构元加权序.
对任意有界模糊数A1与A2为梯形模糊数,即A1=(a1,b1,c1,d1),A2=(a2,b2,c2,d2)A1≤A2的充要条件
(a1+2b1+2c1+d1)≤(a2+b2+c2+d2)
(4)
引理3[16]设A=(a,b,c,d),B=(m,n,p,q)是两个有界梯形模糊数,则
‖A±B‖=‖A‖±‖B‖
(5)

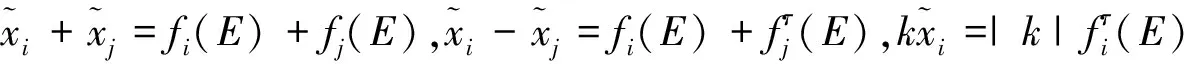

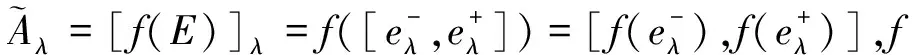
2 一类变量为梯形模糊数的线性规划模型及算例
2.1 一类变量为梯形模糊数的线性规划模型
考虑下列含有模糊数的线性规划问题:
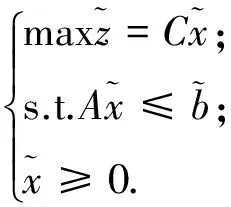
(6)
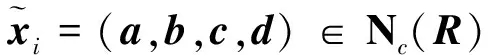
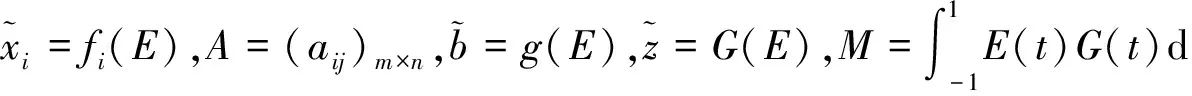
(7)

由结构元理论知:
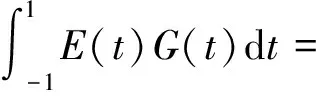
为不失一般性,这里讨论

由引理4可知:
当ci≥0时,有
当ci<0时,则有
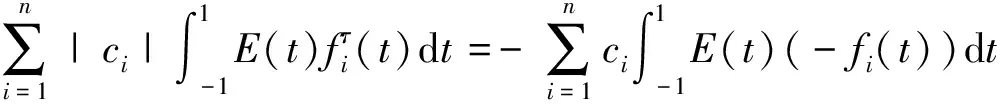
E(-t)=E(t),由积分换元法可以得到:
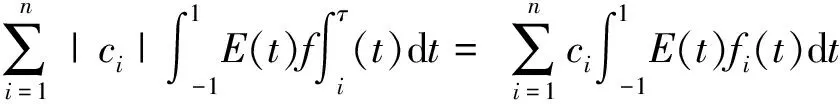
由引理2和引理4得有
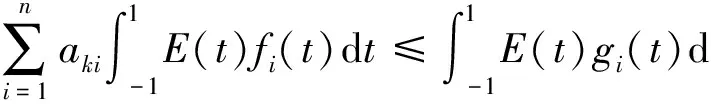
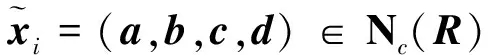
2.2 算法
本文的算法描述如下:
1)若模糊数为梯形模糊数,则能得到它的隶属函数E的表达式,并且可由E(x)=E(f-1(x))求出f(x);
2)计算
并代入模型(6);
3)根据定理3将变量为梯形模糊数的线性规划问题转化为含约束条件的梯形模糊数的线性规划,再根据单纯形方法[14]得到模型(7)的最优解;
4)将模型(7)的最优解代入模型(6)就得到了该问题的最优解.
例1:考虑如下形式的模糊线性规划问题:

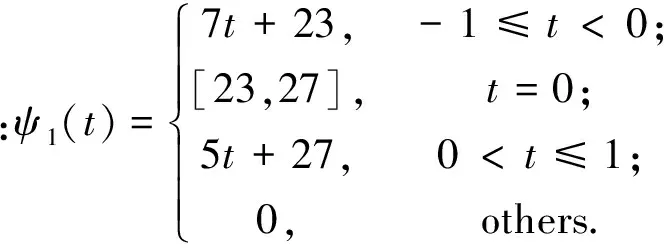

代入原问题,则原问题等价于:
则有模糊最优解为:
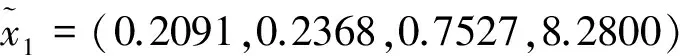


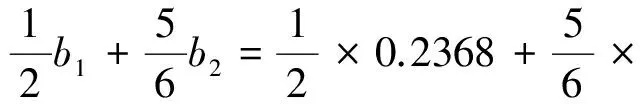


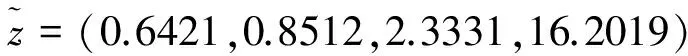
且M=23.2128.
例2:设甲、乙两种产品的产量分布为x1和x2(单位:kg)则该问题的数学模型为
其中:x1=(a1,b1,c1,d1)x2=(a2,b2,c2,d2),a1≤b1≤c1≤d1,
a2≤b2≤c2≤d2则有:
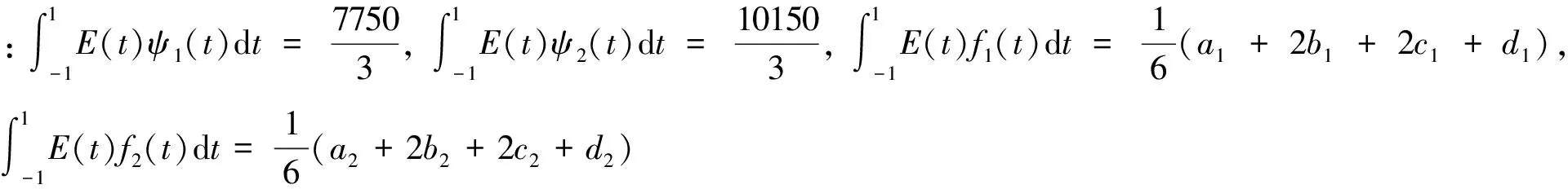
综上所述,则有模糊最优解为:

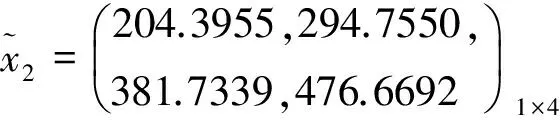




代入原目标函数的该线性规划问题的最优解为z=2366.3
显然,算例避免了运用模糊λ截集理论将变量为模糊数的线性规划问题转化为多目标问题,大大简化了运算.
3 结 论
本文首先利用结构元求出他的隶属函数和单调有界函数;然后利用加权排序法得到有界模糊数的结构元特征数,这就是一个去模糊化的过程,得到了经典的线性规划;证明了模糊线性规划与转换后的经典线性规划之间是等价的,同时证明了它们的最优解也是等价的;再利用线性规划的MATLAB编程求该方程的最优解,从而求出变量为梯形模糊数的线性规划问题的解,简化了运算.
[1] 成亚丽.变量为三角模糊数的线性规划问题研究[J].模糊系统与数学,2010,13(3):6-13. CHENG Liya. Research on the linear programming problem of triangular fuzzy number[J]. Fuzzy Sets and Systems,2010,13(3):6-13.
[2] GUU S M, WU Y K. Two phase approach for solving the fuzzy linear programming problems[J]. Fuzzy Sets and Systems,1999,107(1):191-195.
[3] MALEKI H R, TATA M, MASHINCHI M,et al. Linear programming with fuzzy variable[J]. Fuzzy Sets and Systems,2000,109(1):21-33.
[4] CADENAS J M, VENDEGAY J L. Using ranking functions in multi objective fuzzy linear programming[J]. Fuzzy Sets and Systems,2000,111(1):47-53.
[5] 曾庆宁.模糊系数规划[J].模糊系统与数学,2000,14(3):99-105. ZENG Qingning. Fuzzy Coefficient Programming[J]. Fuzzy Systems and Mathematics,2000,14(3):99-105.
[6] 张超;赵承业.计算树的[1,2]-数的算法研究[J].中国计量学院学报,2015(2):243-246. ZHANG Chao,ZHAO Chengye. Research on the algorithms of computing the [1,2]-number of trees[J]. Journal of China Jiliang University,2015(2):243-246.
[7] 毛保华.线性规划的若干算法研究[D].杭州:杭州电子科技大学,2010. MAO Baohua. Some new algorithms for linear programming[D].Hangzhou:Hangzhou dianzi University,2010.
[8] 李敬华.线性规划的不可行内点算法研究[D].西安:西安电子科技大学,2014. LI Jinghua. Infeasible interior point Algorithms for Linear Programming[D]. Xi’an: Xi dian University,2014.
[9] 邵迎超.模糊数的排序及应用[D].成都:西华大学,2008. SHAO Yingchao. Ranking of fuzzy numbers and its application[D].Chengdu: Xihua University,2008.
[10] 郭嗣宗.模糊分析中结构元方法(Ⅰ)、(Ⅱ)[J].辽宁工程技术大学学报(自然科学版),2002,21(5,6):670-673,808-810. GUO Sizong. Method of structuring element in fuzzy analysis (Ⅰ)、(Ⅱ)[J]. Journal of Liaoning Technical University(Natural Science Edition),2002,21(5,6):670-673,808-810.
[11] 邓胜岳,周立前.求解上层含约束条件且具有模糊决策变量二层线性规划的结构元方法[J].模糊系统与数学,2014,28(6):105-112. DENG Shengyue, ZHOU Liqian. Bi-level multiple followers linear programming with upper constraint and fuzzy decision Variables[J]. Control and Decision,2014,29(10):1803-1809.
[12] 邓胜岳,汪新凡,杨小娟.求解上层含约束条件的模糊二层多随从线性规划的结构元方法[J].湖南工业大学学报(自然科学版),2013,27(5):5-8. DENG Shengyue, WANG Xifan, YANG Xiaojuan. Solving fuzzy bilevel linear programming with multiple followers under upper constraints by structured element method[J]. Journal of Hunan University of Technology,2013,27(5):5-8.
[13] 曾宪阳,马一太,潘江,等.房间空调器性能的模糊综合评判[J].中国计量学院学报,2007(2):146-150. ZENG Xianyang, MA Yitai, PAN Jiang etal, Fuzzy comprehensive assessment of performance of room air conditioners [J]. Journal of China Jiliang University,2007(2):146-150.
[14] 赵海坤,郭嗣宗.全系数模糊两层线性规划[J].模糊系统与数学,2010,24(3):98-106. ZHAO Haikun, GUO Sizong. Bi-Level Linear Programming with All-Coefficient Fuzzy[J]. Fuzzy Systems and Mathematics,2010,24(3):98-106.
[15] 邓岳胜,周立前,汪新凡.上层含约束条件且具有模糊决策变量的二层多随从线性规划[J].控制与决策,2014,29(10):1803-1809. DENG Shengyue, ZHOU Liqian, WANG Xinfan. Bi-level multiple followers linear programming with upper constraint and fuzzy decision variables[J]. Control and Decision,2014,29(10):1803-1809.
[16] 郭嗣琮.基于模糊结构元理论的模糊分析数学原理[M].沈阳:东北大学出版社,2004:10-129.
A linear programming with trapezoidal fuzzy numbers for a class of variables
ZHOU Xihua1, JIA Hongxin1, DENG Shengyue2, WU Yao2
(1.Guangdong Polytechnic of Environmental Protection Engineering, Foshan 528216, China;2.School of Science,Hunan University of Technology, Zhuzhou 412007, China)
A fuzzy number ranking criteria was defined by using structure element to deal with variable fuzzy number fuzzy linear programming problems. The way to deblur about the linear programming of variables with trapezoidal fuzzy numbers and the transformfuzzy linear programming of variable with trapezoidal fuzzy numbers into the classic fuzzy linear programming was discussed. It is proved that the optimal solution of the model is equivalent to the optimal solution of the classical linear programming. The optimal solution was obtained by reusing the simplex algorithm. And the algorithm of solving this kind of model was designed.The feasibility of the method and the validity of the algorithm were verified by two examples.The study provides a new method for the study of the generalized fuzzy linear programming problem with fuzzy variables.
fuzzy structured element; fuzzy linear programming; the optimal solutio
2096-2835(2016)04-0480-07
10.3969/j.issn.2096-2835.2016.04.021
2016-09-01 《中国计量大学学报》网址:zgjl.cbpt.cnki.net
湖南省自然科学基金资助项目(No.2016JJ2043),湖南省教育厅科学研究项目(No.16C0472,15C0537),广东环境保护工程职业学院院级教研教改课题(No.2015YZPT25).

O221.1
A

