基于近似投影的分布式零阶Push-Sum优化算法

任芳芳，李德权

安徽理工大学理学院，安徽淮南，232001

基于近似投影的分布式零阶Push-Sum优化算法

任芳芳，李德权

安徽理工大学理学院，安徽淮南，232001

近似投影；分布式优化；零阶方法；分布式算法；非平衡网络

1 问题提出

近年来，多个体分布式凸优化问题成为多个体优化问题的一个研究热点。和以往的集总式算法相比，分布式算法在解决很多大规模计算问题中有很大优势。集总式算法是指在多个体系统中所有个体并不发挥同样的作用，而是其中某个个体处于中心地位，负责接收并处理其他个体的数据信息。而分布式算法主要是指在多个体系统中每个个体都处于相同的地位，相邻个体之间进行信息交流，最终达到优化的目的。分布式优化在很多领域如大规模机器学习、分布式跟踪与定位以及无线传感网络都有广泛的应用。

文献[1]最早给出了对分布式优化算法的分析，即基于一致性算法的分布式次梯度算法。为了进一步研究约束优化问题，文献[2-3]给出一种基于一致性算法的原始对偶次梯度方法以及分别在等式和不等式约束下的原始对偶算法。文献[4]提出了分布式对偶平均优化算法。此外，投影算法在分布式优化问题中也有重要的应用，例如文献[5]提出了投影次梯度算法;对于投影无法准确计算的情况，文献[6]给出了一种近似投影一致性算法。然而，以上算法都是适用于多个体系统中的每个个体对应的目标函数的梯度信息可以获得或者投影可以准确计算的情况，在另外一些情况下，个体对应的目标函数的梯度无法获得或无法计算[7]，投影也仅能近似得到[8]，针对这两种问题，文献[9]给出了一种基于近似投影的零阶分布式优化算法。而文献[8]仅仅研究了基于单变量通信的系统。

考虑多个体网络无线通信的广播特性，基于双变量通信的Push-sum算法引起了学者的广泛兴趣[9-12]。和单变量通信相比，基于双变量通信的Push-sum算法能够更有效地利用无线广播的性质并可以应用于非平衡网络，使得优化算法在非平衡网络中依然收敛。因此，研究基于近似投影的分布式零阶Push-sum优化算法具有很大的意义。

2 符号说明

3 问题描述

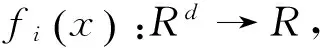
(1)

记问题(1)的最优值F*是一个有限的确定值，并记其最优解为：

4 算法介绍

基于近似投影的分布式零阶算法[8]表示如下：

对于任意k≥0，有：

(2)

(3)

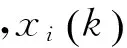
为了更有效地利用无线广播的性质,并将多个体分布式优化算法应用于非平衡网络，使优化算法在非平衡网络中依然收敛，提出基于近似投影的分布式零阶Push-sum优化算法：

(4)

(5)

(6)

(7)

(8)

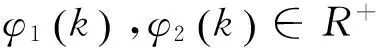
5 收敛性分析

假设1对每一个i∈V，函数fi是X上的Lipchitz连续函数且Lipchitz常数为Li，即：

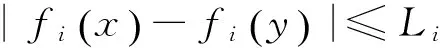
假设2存在一个正整数B，使得有向图(V,E(A(kB))∪…∪E(A((k+1)B-1)))对所有k≥0都是强连通图并且B是强连通周期。

引理1令Fk是一个随机变量，且满足Fk={(xi(0),i∈V);(u1,i(τ),u2,i(τ),i∈V),0≤τ≤k-1)且F0={xi(0),i∈V}。

(1)梯度的预测值满足：

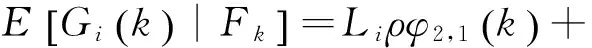
(3)存在一个常数使得下式成立：

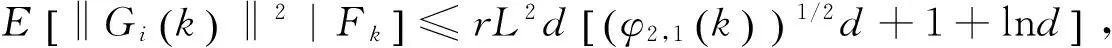
(9)

定理1 在假设1,2,3和引理1成立的情况下，对于任意i∈V和k≥0，有下式成立：

(10)

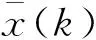
(11)

(12)

(13)

令z为一个辅助向量，则由(13)可得：

(14)

由引理1(1)可得：

(15)

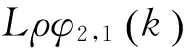
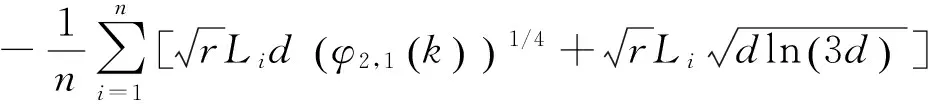
(16)

又因为

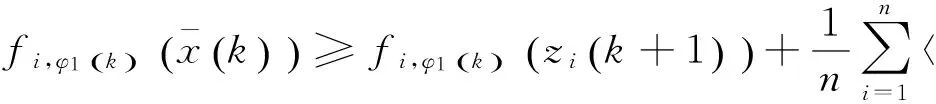
(17)

故可得：

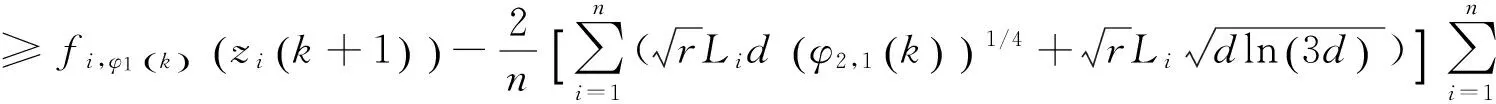
(18)

另一方面，

综上可得：

(19)

(20)

两边同时除以2α(k+1)，可得：

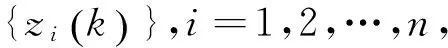
(21)

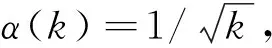
(22)

证明：由引理2可得：

(23)

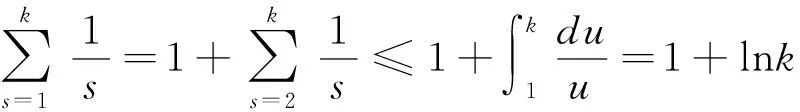
(24)

(25)

将(25)式代入(23)式，故(22)式成立。

定理2 在假设1,2,3成立，定理1和推论2也成立的前提下：

(26)

证明：首先定义一个序列

(27)

由假设1及引理1可得：

(28)

由定理1中(14)可得：

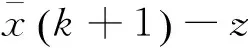
则有：

(29)

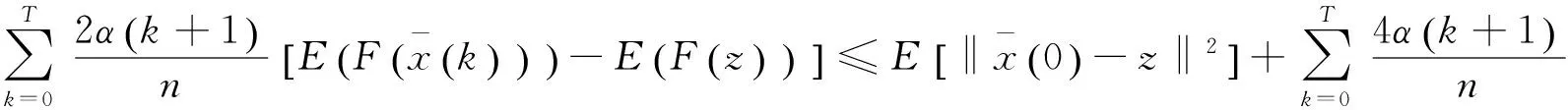
(30)

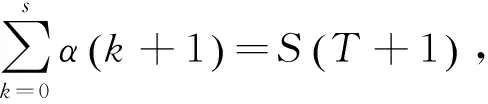
(31)

令z=z*，则：

(32)

将推论2中(22)式代入(32)式可得：

(33)

综上(28),(33)式，最终可得：

5 结束语

在文献[9,10]的基础上，本文研究了基于近似投影的分布式零阶Push-sum优化算法，首先给出基于近似投影的分布式零阶优化算法，针对有向非平衡网络，结合Push-sum算法并最终证明了其收敛性。此外，本文还有一些问题有待解决，比如时延情形下的优化算法。

[1]Nedic A,Ozdaglar A.Distributed subgradient methods for Multi-Agent optimization[J].IEEE Transactions on Automatic Control,2009,54(1):48-61

[2]ZHU Minghui,MartInez S.On distributed convex optimization under inequality and equality constraints via primal-dual subgradient methods[J].IEEE Trans.autom.control,2010,57(1):151-164

[3]YUAN D,XU S,ZHAO H.Distributed Primal-Dual subgradient method for multiagent optimization via consensus algorithms[J].IEEE Transactions on Systems,Man,and Cybernetics.Part B,Cybernetics :a Publication of the IEEE Systems,Man,and Cybernetics Society,2011,41(6):1715-1724

[4]YUAN De-ming,XU Sheng-yuan,ZHAO Huan-yu,et al.Distributed dual averaging method for multi-agent optimization with quantized communication[J].Systems & Control Letters,2012,61(11):1053-1061

[5]Lee S,Nedic A.Distributed random projection algorithm for convex optimization[J].IEEE Journal of Selected Topics in Signal Processing,2013,7(2):221-229

[6]LOU You-cheng,SHI Guo-dong,Johansson K H,et al.Approximate projected consensus for convex intersection computation:convergence analysis and critical error angle[J].IEEE Transactions on Automatic Control,2014,59(7):1722-1736

[7]Nesterov Y,Spokoiny V.Random Gradient-Free minimization of convex functions[J].Foundations of Computational Mathematics,2015,36(16):1-40

[8]Duchi J C,Jordan M I,Wainwright M J,et al.Optimal rates for Zero-Order convex optimization:the power of two function evaluations[J].IEEE Transactions on Information Theory,2013,61(5):2788-2806

[9]YUAN Deming,Ho D W,XU Shengyuan.Zeroth-Order method for distributed optimization with approximate projections[J].IEEE Transactions on Neural Networks and Learning Systems,2016,27(2):284-294

[10]Nedic A.Olshevsky A.distributed optimization over Time-Varying directed graphs[J].Automatic Control,IEEE Transactions on,2015,60(3):601-615

[11]Boyd S,Ghosh A,Prabhakar B,et al.Randomized gossip algorithms[J].IEEE Transactions on Information Theory,2006,52(6):2508-2530

[12]张晓倩，李德权．有向网络异步PUSH-SUM次梯度优化算法的研究[J]．皖西学院学报，2014(5)：11-15

[13]Iutzeler F,Ciblat P,Hachem W.Analysis of Sum-Weight-Like algorithms for averaging in wireless sensor networks[J].IEEE Transactions on Signal Processing,2013,61(11):2802-2814

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2016.03.026

2015-11-30

国家自然科学基金(61472003)；国家自然科学青年基金(11401008)；安徽省教育厅自然科学研究重点项目(KJ2014A067)。

任芳芳(1990-)，女,安徽宿州人，在读硕士研究生，主要研究方向：分布式优化理论与应用。

TP13

A

1673-2006(2016)03-0100-07