土壤含水率监测数据误差分析与修正

王娟娟

(新疆金达鑫工程建设有限公司，新疆 库尔勒 841000)

土壤含水率监测数据误差分析与修正

王娟娟

(新疆金达鑫工程建设有限公司，新疆 库尔勒 841000)

土壤墒情自动监测设备能够快速、高效、连续地观测土壤墒情数据,但由于受设备自身状态、以及田间环境变化的影响,在长期连续监测中输出数据的准确性和稳定性会逐渐降低,不利于墒情监测业务的开展。本文通过分析土壤墒情自动监测数据的误差特点,构建了一元一次、一元二次和一元三次差分方程对自动监测数据进行误差修正,并对修正后的误差特征进行分析。结果表明:经过差分修正后,20c m深度的绝对误差均值减小了34%,40c m深度的绝对误差均值减小了67%,自动监测数据误差显著下降;3种差分方程中线性差分方程表现最优。通过差分方法来修正自动监测数据简单易行,能有效的提高自动监测数据精度,提高监测体系整体性能。

土壤含水率;误差分析;误差修正;差分方程

水在土壤中的运动是水循环中的重要环节，影响着整个生物圈的水分、能量和物质流动，土壤水分也是植被生长的主要水分来源，因此土壤墒情的监测对水循环研究、农牧灌溉管理、水资源高效利用以及抗旱等工作都具有重要的意义［1，2］。

对比各种土壤水分测量方法，各自的优点和缺点可以总结如下:直接测定方法(烘干称质量法)准确且经济，但测定过程具有破坏性、耗时、切不可重复，因此空间覆盖范围有限;间接测量方法的适用性取决于成本，精度，响应时间，设备安装、管理和耐久性;利用时域反射(T D R，T i m eD o m a i n R ef l e c t o m e t r y)、频域反射(F D R，F r e que nc yD o m a i n R ef l e c t o m e t r y)和地质雷达(G P R，G r o und P e ne t r a t i ng R a da r)可以及时获取较准确的数据。随着土壤水分传感器以及相关的设备保障、数据传输技术的成熟，基于T D R和F D R的土壤墒情自动采集设备得到了广泛应用，其定点长期连续观测能力使得土壤墒情监测的空间和时间范围都得到了延伸。但与人工进行烘干称质量测得的数据相比，自动设备采集到的数据精度和稳定性仍然限制着其业务化应用［3，4］。

在实际土壤墒情监测中，一般认为传统的烘干法测得的土壤含水率数据是准确可信的，可以作为其它各种土壤含水率测量方法的校正标准，而自动监测站长期连续观测对于研究土壤水分的时空变化规律又有重要作用［5］。因此，土壤含水率的自动监测和人工监测往往是按照不同监测频率同时进行以发挥各自的优势，提高监测系统整体的观测水平。通常人工监测点数量较少采样间隔较长，自动监测点较多采样间隔较短，并且2种监测在时间和空间上具有一定的重叠度，这就为使用人工监测数据来修正自动监测数据提供了前提条件。本文以连续的人工和自动土壤墒情监测数据为基础，通过分析自动监测数据的误差特征，实现提高自动监测数据精度的目标。

1 数据来源与方法

1.1 数据来源

本研究使用的数据包括土壤墒情自动监测设备获取的土壤体积含水量数据和人工采用烘干称质量法测定并转换为体积含水量的数据。自动监测设备采用探头式传感器(H y dr a土壤水分/盐分/温度速测仪)，在土壤深度为20、40、60、80与100c m处埋设土壤水分传感器，设备以1次/h的频率测定土壤水分含量，并将数据储存在设备中，采用笔记本电脑定期下载数据。

对各层人工对比监测数据和仪器监测值按最小二乘法拟合一元二次多项式作为标定公式，即:

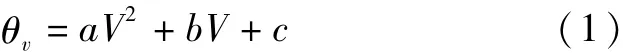
式中:θv—土壤体积含水率，%;V—传感器输出电压，V;a，b，c—二次项、一次项和常数项回归系数。

人工监测数据的采样点取土钻孔的位置分布在传感器埋设位置四周半径10～15c m之间的范围内，只测定20和40c m深度的土壤含水量，取土样时间为每月5、15和25日8时，通过烘干称质量计算得到质量含水率后再换算为体积含水率作为采样当天的土壤含水率进行记录。

标定完成后进行了6个月的人工对比观测，人工测定值与仪器测定值之差的多次平均值的绝对误差要小于等于5%才能达到业务化运行标准。

1.2 数据分析

人工和自动监测数据是采用2种不同方法对同一区域土壤水分含量测定的结果，理论上2者应该是相等的。由于各自测定过程中存在着多种误差，因此实际上2者很难相等，但2组数据应该表现出较强的线性相关性。对人工和自动监测数据计算线性相关系数，结果见表1。

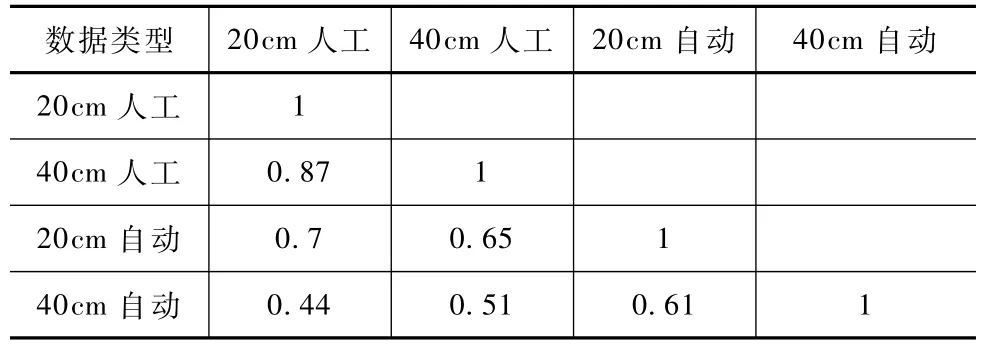
表1 人工和自动土壤含水率数据相关系数

人工监测数据与自动监测数据在20c m深度的相关系数为0.7，表明有较高的相关性，在40c m深度相关系数为0.51，表现为中度相关，由此可见，在40c m深度自动监测数据的精度较差。计算自动监测数据的绝对误差均值，并计算误差的标准差、最大、最小、极差和均值，结果见表2。

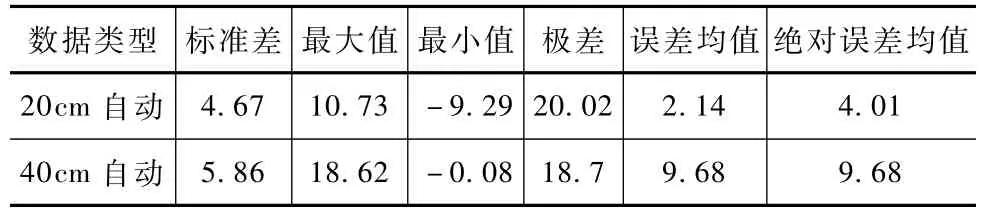
表2 土壤含水率自动监测数据的误差统计值 %

自动监测设备所测得的土壤体积含水率与人工监测土壤体积含水率值之差的多次平均值的绝对误差小于等于5%才能投入业务化运行。20c m自动监测数据的绝对误差均值为4.01%，符合业务运行精度要求，40c m的绝对误差均值为9.68%，超过限定值，无法满足业务运行需求。20和40c m数据的极差都接近20%，表明自动监测数据的稳定度较差，很难满足监测业务的需求。

1.3 误差修正模型

自动监测数据中的误差来源有很多，很难从误差的综合体现中针对每一种来源进行误差的估计和修正。因此，本文按照误差的特性将误差分为随机误差和系统误差2类进行分析和处理。随机误差的出现没有确定规律但多次测量具有一定统计规律，其分布符合正态分布，算数平均值趋于0，因此可以通过求均值的方式消除其影响。系统误差可能是由于传感器性能下降、供电等其他系统性故障、测量设备安装环境因素变化等造成，这些因素从形成到增大甚至到消失通常会持续一段时间，其影响也不是随机出现或消失，而是一旦出现后就会持续作用一段时间。因此在系统性误差的时间序列中，一个时间节点的误差大小与其前后的误差值是相关的，可以定义为其前后误差值的函数，以此来推导该节点误差值的大小，该推导函数即为差分方程。本文正是基于差分方程来对自动墒情监测数据进行系统误差的估计和修正，通过算数平均值来修正随机性误差。

2 结果与讨论

2.1 误差修正结果

本文采用了一元一次方程(式(2))、一元二次方程(式(3))和一元三次方程(式(4))3种类型的差分方程，对其误差修正效果进行对比:

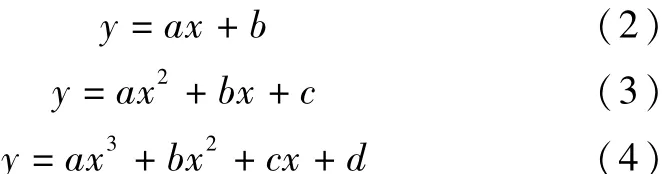
式中:y—绝对误差值，%;x—时间，d;a，b，c，d—方程系数。

差分方程的参数值是通过已知数据点求解而非最小二乘法拟合获得，因此3种方程参数的求解分别需要的数据点个数为2、3和4个。在监测数据的序列中，每间隔一个时间点取一个数据用于构建差分方程，其他数据用作结果检验。采用差分方程对检验数据进行修正后，重新计算绝对误差均值及误差的统计值(见表3)，以分析误差修正的效果。

2.2 结果分析

对比误差修正前后的绝对误差均值的变化，无论采用哪种差分方程该值均减小，其修正后的绝对误差均值都小于5%的要求，可以满足业务运行的精度要求。在20c m深度数据中:采用线性差分方程的修正结果绝对误差均值最小，达到2.65%，与修正前相比减小比例达到了34%;其次为一元三次差分方程，达到2.97%;最后为一元二次方程，达到3.38%。在40c m深度数据中:线性差分方程修正结果的绝对误差均值仍是最小，达到3.20%，与修正前相比减小比例达到67%;其次为一元二次方程，达到3.42%;最后为一元三次方程，达到4.13%。

表3 不同差分方程修正后土壤含水率监测数据误差统计值

经过误差修正后各组数据的误差均值均有大幅减小，更接近于0，对于误差均值的修正，线性方程表现最优，其次是一元二次方程，最后为一元三次方程。

对比不同差分方程的效果，线性差分方程较其他2种方程更优。从建立误差修正模型的原理来看，一个数据项的误差与其前后数据项的误差是相关的，基于该假设采用其前后的数据项的误差来推导该点的误差。建立线性差分方程只需要2个已知误差的相邻数据项，差分方程的时间跨度较小，时间范围内的误差相关性紧密。建立一元二次和一元三次差分方程分别需要3和4个已知误差的相邻数据项来构建差分方程，差分方程时间跨度较大，时间范围内的误差相关性变小。因此，线性差分方程总体的修正效果更好，但正是由于时间跨度大，二次和三次差分方程对误差整体有更大的调节作用，使得它们在降低误差的极差和标准差上表现更好。

综上所述，采用差分方程对自动土壤水分数据进行修正后，绝对误差均值明显减小，监测精度显著提高;系统性误差得到了很好的控制，剩余误差符合随机误差统计规律;差分修正后误差标准差和极差没有明显减小;线性差分方程较其他2种方程修正效果更优。

2.3 误差修正流程

基于对误差组成的分析、误差修正模型的构建以及模型修正效果的验证，可以梳理出基于人工和自动同步墒情监测系统中自动监测数据误差修正的技术流程:在有人工监测的时间点，将自动监测数据进行处理，得到与人工监测在时间和监测目标上对应的监测值;以人工监测数据为真值，计算自动监测数据在各时间点的误差，以相邻2个时间点的数据建立线性差分方程，用该方程计算这段时间间隔内自动监测数据各点的误差估计值;使用该值修正自动监测数据，生成修正后的自动监测数据记录;需要说明的是，在利用自动监测数据时，尽可能采用日均值等算数平均值形式，有利于降低修正后仍然存在的随机性误差，并提高监测系统对缺测数据的容错性。

3 结论

通过对人工和自动连续监测数据的分析可以得出，在自动监测设备长期运行过程中，数据精度可能出现不满足业务运行要求的情况，误差分布也不符合正太分布，存在较明显的系统误差。通过差分方程对自动监测数据进行修正后，20c m深度的绝对误差均值减小了34%，40c m深度的绝对误差均值减小了67%，3种差分方程中线性方程修正效果最优。

自动监测设备的快速连续监测优势是人工监测无法比拟的，人工监测数据的精度和认可度最高，将2种监测手段结合可发挥各自优势，有利于保障墒情监测工作的顺利开展。基于差分方程来对自动监测数据进行修正，计算过程简单易于实施，能够明显提高数据精度，扩展数据应用的深度和广度。同时通对自动监测数据误差的分析，能够为监测设备管护提供支持，帮助改进设备和提高安装调试水平。

［1］陈颂平.甘肃中东部黄土高原土壤水资源的有效利用［J］.水利技术监督，2009(05):22-23.

［2］王剑影.水环境监测参数与选用标准对照表［J］.水利技术监督，2004(04):53-63.

［3］王旭东，路军.墒情监测及节水灌溉自动控制系统开发与应用［J］.水利技术监督，2006(02):38-39.

［4］宋虹兵.开都-孔雀河流域水量监测方案设计［J］.水利技术监督，2014(06):17-20.

［5］董婷婷，于燕.辽宁省旱情监测预警与评估系统设计与实现［J］.水利技术监督，2014(06):43-46.

S152.7+3

A

1008-1305(2016)05-0047-03

10.3969/j.issn.1008-1305.2016.05.018

2016-03-04

王娟娟(1981年—)，女，工程师。