压缩感知在电能质量扰动信号中的研究

李瑞明，王 铮

(太原工业学院计算机工程系，山西 太原 030008)

压缩感知在电能质量扰动信号中的研究

李瑞明，王 铮

(太原工业学院计算机工程系，山西 太原 030008)

压缩感知理论可以解决传统采样方法中采样数据量大、采样时间较长以及压缩复杂度高的问题，因此在图像压缩、电能质量分析、信号处理领域得到了广泛的应用。因此，本文对其理论以及在电能质量分析中的应用与展望进行了综述。首先对压缩感知的基本原理进行了阐述，并对压缩感知的三个关键部分进行了介绍，对其在电能质量研究领域的现状进行重点介绍，最后对其在电能质量的深入应用进行了展望。

电能质量扰动信号；压缩感知；稀疏表示；重构算法

电压波形为理想正弦波、并且幅值、频率恒定，则可以构成一个可靠的供电系统[1]。但实际的电能输送过程，由于不对称负荷、冲击性负荷的影响，会使电网的干扰信号不断增加，从而影响电能质量，因此，需要对电能质量扰动信号进行研究[2-4]。传统电能质量信号的采样方法均基于Nyquist采样定理，采样数据量大、采样时间较长，并且存在压缩复杂度高、恢复算法不易实现的问题。

关于电能质量扰动信号的分析方法，主要有傅里叶变换、小波变换、Prony算法、S变换以及Hilbert-Huang变换等。其中，傅里叶变换一般用于分析稳态电能信号，存在频谱泄露和栅栏效应。文献[5]采用Prony算法对电能质量扰动信号进行分析，采用该算法精度比较高，但是容易受到噪声的影响。文献[6-8]分别采用小波法及改进小波法对电能信号进行分析，此类方法可以对电能质量暂态信号进行比较准确的分析，但和Prony算法一样，基于Nyquist定理进行采样，需要进行大量数据的采样，并且数据的压缩复杂度也比较高。S变换结果只包含幅值信息，不能对频率变化和谐波的相关参数进行估计与测量[9]，HHT具有自适应性，但只对连续信号进行解析分析。

针对传统采样理论以及信号处理方法的不足，压缩感知理论逐渐被应用到电能质量分析中[10-13]，本文首先对压缩感知理论进行了阐述，进行了不同恢复算法的信号重构，简单分析了不同算法的重构效果以及性能指标，最后对压缩感知在电能质量扰动信号中的应用进行了展望。

1 压缩感知理论

压缩感知理论的主要思路为：如果一维源信号在某域内具有K-稀疏性(K小于源信号的长度)，则可对源信号进行压缩观测，然后采用重构算法对稀疏观测后的矩阵进行重构。图1为压缩感知理论的基本结构图：

图1 压缩感知理论基本结构

2 国内外研究现状

压缩感知理论将满足稀疏性的信号进行压缩，进而采用重构算法对压缩后的信号进行重构，既可以降低信号数据的存储与传输，又能降低对硬件的要求，因此，受到了国内外专家的普遍关注[14]。现在，压缩感知理论在图像与模式识别、无线传感网络等领域得到了广泛的应用。

压缩感知理论包括三大核心：信号的稀疏性、压缩观测和重构算法。其中，源信号满足稀疏性是应用压缩感知的前提，并且需要寻找与稀疏基不相关的观测矩阵对原始信号进行压缩观测，然后采用算法对压缩观测信号进行重构从而重构源信号。

2.1 信号的稀疏表示

信号的稀疏性是进行压缩采样的前提，其决定了压缩采样的个数、算法的复杂度以及信号的重构精度。目前稀疏表示主要有稀疏字典与稀疏分解算法两种。

1) 稀疏字典：稀疏字典包括正交基字典和超完备冗余字典。正交基变换结构简单、算法复杂度低，但不能对复杂信号稀疏度进行准确表示。超完备冗余字典可以准确的对源信号稀疏性进行表示，超完备字典的原子种类包括Ricker子波、Chirplet、Curvelet、FMmlet、Contourlet、各向异性精细原子等[15]。

2) 稀疏分解算法：稀疏分解算法在不改变信号特征的情况下选取稀疏度最好的原子对信号进行稀疏表示，包括基追踪算法和贪婪算法。其中，基追踪算法可以实现全局最优化，但是算法复杂，主要用于解决凸优化问题；贪婪算法需对信号实时投影计算，包括匹配追踪法、正交匹配追踪算法、迭代阈值法以及智能优化算法等[16]。

2.2 观测矩阵

观测矩阵是实现压缩感知算法的关键。观测矩阵需要满足硬件容易实现、采样复杂度低等优点，并且与稀疏基具有不相关性。其中，随机观测矩阵、确定性观测矩阵和自适应观测矩阵在压缩感知中应用最多。

2.3 重构算法

由压缩感知算法可知，对原始信号的重构就是求解最优问题。常用的重构算法有凸松弛算法、贪婪追踪算法和组合算法[17]。

凸松弛算法将非凸问题转化为凸问题，进而对最优值进行求解，包括BP算法、内点法、梯度投影方法和迭代阈值法，该算法所需观测点数少，计算量较大。贪婪算法以上一步的局部最优值进行迭代对信号进行重构，该算法包括匹配追踪算法、正交匹配追踪算法、分段OMP算法和正则化OMP算法。该类算法的实现时间比较长，且重构精度与算法实现时间相关。组合算法要求信号的采样支持通过分组测试快速重建，主要包括傅里叶采样、链追踪和HHS追踪等。目前，粒子群算法以及改进粒子群算法也逐渐被应用到信号的重构中[18]。

3 在电能质量扰动信号中的应用

由于传统采样方式的固有缺点，压缩感知理论逐渐被应用到电能质量扰动信号中，包括压缩采样与信号重构。主要采用傅里叶变换基、二维小波基作为变换基进行压缩采样，观测矩阵一般采用变密度采样模板和高斯随机矩阵，信号的重构算法则选用基于TV最小化共轭梯度法、MP算法、OMP算法、快速贝叶斯匹配追踪法(FBMP)等作为重构算法对电能质量扰动信号进行重构。

本文以电压突降为例，分别采用OMP、ROMP以及SPG恢复算法对原始信号进行重构，并对其重构效果和压缩性能指标进行比较。重构效果如图2、3、4所示。

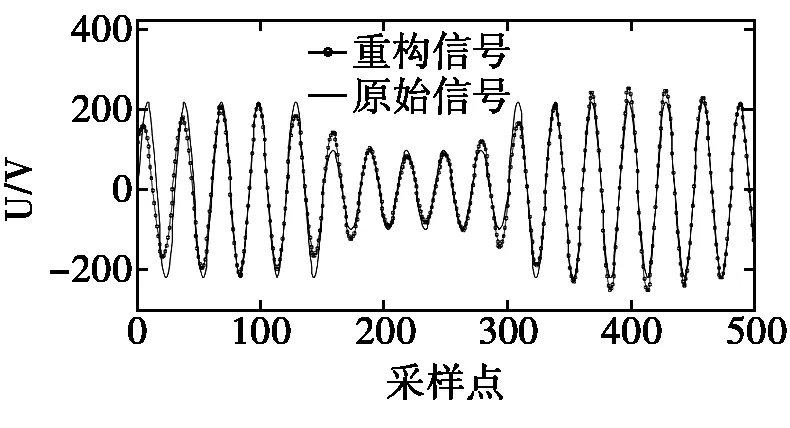
图2 基于OMP算法的电压突降信号重构

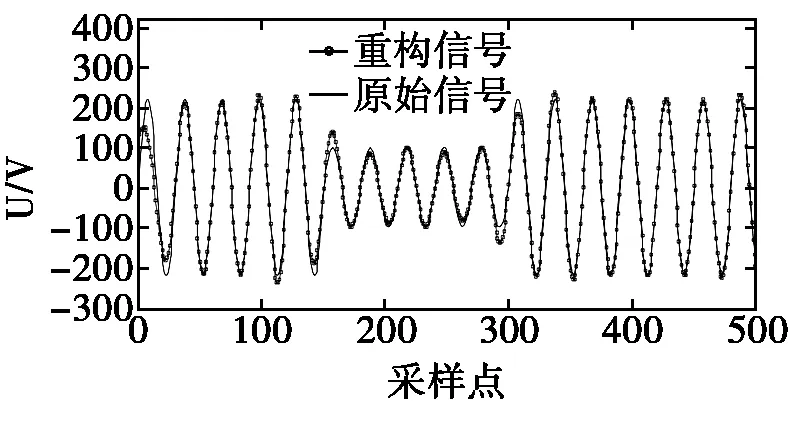
图3 基于ROMP算法的电压突降信号重构

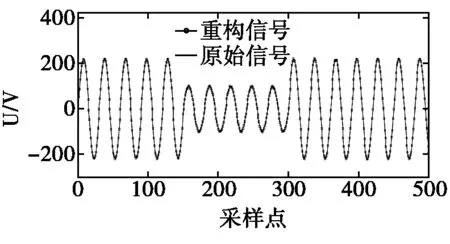
图4 基于SPG算法的电压突降信号重构

由图2、3可知，以OMP算法、ROMP算法为代表的贪婪算法在重构精度上都比较低。SPG算法由于运用谱投影梯度方法计算更新方向与步长，引进非单调性搜索策略使算法具有全局收敛性，从而达到重构精度与算法效率的平衡。由图4可以看出，重构信号与原始信号几乎完全重合，因此其重构精度远远高于OMP算法、ROMP算法为代表的贪婪算法。

并且，由运行结果可知以SPG为代表的凸优化算法的压缩性能指标高于贪婪算法，但是SPG恢复算法由于算法复杂度比较高，因此运行时间相对要长一点。

4 总结与展望

压缩感知理论突破了传统采样方式的限制，大大减轻了数据采样的压力，因此在电能质量分析领域得到了应用。但是，压缩感知理论应用的前提是采样信号在某域内满足稀疏性，并且在构造观测矩阵时需要考虑观测矩阵与稀疏矩阵具有不相关性。在选择恢复算法时，既要考虑算法重构精度也要考虑算法的复杂度以及由此引起的运行效率。因此，对于基于压缩感知理论的电能质量扰动分析，仍存在以下问题：

1) 电能质量扰动信号的稀疏性是进行压缩采样的前提，对于不同时刻、不同时间长度的扰动，信号的稀疏度是否不同？应如何考虑？

2) 恢复算法的设计，凸优化算法与智能优化算法已经达到了很高的重构精度，但是未考虑其硬件的可行性，尤其对于智能优化算法来说。

3) 恢复算法仅对原始信号进行重构，并没有对扰动发生与结束的时间进行判断。

4) 仅考虑扰动信号基波情况，并没有考虑其多次谐波时的重构精度以及算法的运行效率。

基于此，压缩感知理论在电能质量扰动信号中的深入应用仍有很大的研究空间。

[1] 林海雪.现代电能质量的基本问题[J].电网技术，2001,25(10):5-12.

[2] 肖湘宁.电能质量科技发展动态及其分析[J].大功率变流技术,2010(1):25-30.

[3] 冯宇，唐轶，石延辉，等.电能质量分析与参数估计的研究方法综述[J].电力系统及其自动化学报,2010,22(3):78-85.

[4] 林涛，刘林，曹健，等.智能电网技术框架下的电能质量监测与分析技术综述[J].电器与能效管理技术,2009(21):1-6.

[5] 丁屹峰，占勇，程浩忠，等.基于Prony算法的扰动电能质量扰动信号分析[J].上海交通大学学报,2005,39:36-38.

[6] 李涛，夏浪.基于小波分形的电能质量扰动多分辨率分析[J].湖南大学学报,2010,37(1):80-84.

[7] 何顺忠.采用Meyer小波变换的电能质量扰动信号的检测与时频分析[J].黑龙江电力,2004,26(6):454-457.

[8] 何正友，陈小勤.基于多尺度能量统计和小波能量熵测度的电力扰动信号识别方法[J].中国电机工程学报，2006，26(10)：33-39.

[9] Granados-Lieberman,Romero-Troncoso R J,Osornio-Rios R A,et al.Techniques and method-ologyies for power quality analysis and disturbances classification in power systems:a review[J].IETGeneration,Transmission & Distribution，2011,5(4)：519-529.

[10] Cand’s E. Compressive Smpling[C].Madrid:Proceedings of the International Congress Mathematicians,2006:1433-1452.

[11] Cand’s E,Tao T.Near Optimal Signal Recovery from Random Projections:Universal Encoding Strategies[J].IEEE Tran on Information Theory,2006,52(12):5406-5425.

[12] Donoho DL.Compressed Sensing[J].IEEE Tran on Information Theory,2006,52(4):1289-1306.

[13] 朱云芳，戴朝华，陈维荣，等.压缩感知理论及其电能质量应用与展望[J].电力系统及其自动化学报，2015，27(1)：80-85.

[14] Eldar Y C,Kutyniok G.Compressed Sensing：Theory and Applications[M].Cambridge：Cambridge University Press，2012.

[15] 蔡泽民，赖剑煌.一种基于超完备字典学习的图像去噪方法[J].电子学报,2009,37(2):347-350.

[16] 方红，杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421.

[17] 陈旗，曹汉强，方标，等.基于OMP的非合作宽带脉冲压缩雷达言号的压缩感知研究[J].信号处理,2012,28(6):900-906.

[18] 梁丹亚，李宏伟，王克，等.粒子群优化的GPSR-BB压缩感知重构算法[J].空军工程大学学报:自然科学版,2015(1):81-84.

Research on Compressive Sensing in Power Quality Disturbance Signal

Li Ruiming, Wang Zheng

(DepartmentofComputerEngineering,TaiyuanInstituteofTechnology,TaiyuanShanxi030008,China)

To solve the shortage of large volumes of stored data, high complexity of compression in traditional method, compressed sensing is widely applied in image compression, power quality analysis and signal processing. Therefore, this paper reviews its application and prospect in the analysis of power quality. Firstly, signal sparse decomposition and compressed sensing are surveyed, including their basic concepts. Then, three crucial issues of compressed sensing theorem are introduced. And the application status of compressed sensing theory in power quality analysis is specially presented. Moreover, this paper compares the reconstruction result using different recovery algorithm. Finally, the future research prospects on compressed sensing of the power quality disturbance signals are introduced.

power quality disturbance signals; compressed sensing; sparse representation; reconstruction algorithm

2016-09-21

李瑞明(1989- )，男，助教，硕士学位，研究方向：算法研究。

1674- 4578(2016)06- 0077- 03

TP274

A