基于多链路权值减小的动态SPT算法研究

郭文强，肖乾才，李明奇

（1.新疆财经大学 计算机科学与工程学院，新疆 乌鲁木齐 830012；2.电子科技大学；四川 成都 611731）

基于多链路权值减小的动态SPT算法研究

郭文强1，肖乾才2，李明奇2

（1.新疆财经大学 计算机科学与工程学院，新疆 乌鲁木齐 830012；2.电子科技大学；四川 成都 611731）

分支更新的动态最短路径算法可以有效提高动态最短路径计算的效率。通过分析动态最短路径算法研究的现状和问题，文章对Nfixed（v）的定义进行了改进，解决了原算法中的边检查冗余问题，改进了MinD和MaxR算法边检查步骤，有效地减少了重复检查次数。仿真结果显示，改进后的算法具有更高的效率。

线性规划；网络拓扑；路由协议；动态最短路径算法；动态更新算法

在当今的互联网中，数据报文由路由器根据转发表进行转发。转发表的构建则由路由协议在网络拓扑变化同步后更新路由得到。链路状态路由协议通过路由器之间洪泛拓扑信息形成同一拓扑数据库，之后计算最短路径树进而计算路由，然后将路由下发形成转发表，如OSPF[1]（开放最短路径优先）以及IS-IS[2]（中间系统对中间系统）协议。

当拓扑变化后，标准的最短路径算法Dijkstra算法[3]无法判断改变的拓扑结构对已有SPT的作用范围。只能全部重新计算。若变化的拓扑较少，实际上变化拓扑对SPT的影响较小，全拓扑计算不仅效率低，而且导致路由不稳定。这种无法判断变化拓扑对最短路径树的影响范围而只能进行全拓扑计算的最短路径算法叫作静态最短路径算法。动态最短路径算法则根据变化的拓扑更新SPT上受影响的节点，不受影响的节点无需更新，从而提高了拓扑计算的效率与路由的稳定性。根据算法处理变化拓扑的数量，动态最短路径算法可分成两类：多条边的权值发生改变的边更新算法；单条边的权值发生改变的点更新算法[4-6]。

McQuillan等[7]最早提出的一个最短路径动态更新算法，与P.Narvaez提出的King算法[8]在原理与思想上类似。但是，文献[8]中的情况仅适用于Dijkstra算法的动态最短路径问题。而King算法则对它进行了改进，使之可应用于Bellman-Ford，D’Esopo-Pape，Dijkstra等静态算法，是一种通用的最短路径动态算法的框架。

由于网络中边的权值增大或减小对最短路径树的产生的影响不同，动态算法将边权值的增大和减小采用不同的处理办法，将只能处理边权值增大或者减小一种变化的算法叫作半动态算法，而将可以同时处理边权值增大和减小的算法叫作全动态算法。

将变化的拓扑结构分为两类[9-11]：串行变化拓扑和并行变化拓扑。可以证明并行变化拓扑能够一次性更新完毕，而串行变化拓扑则存在错误。同时不能得到一种有效的方法对变化边的串并行关系进行判断。因此，不能处理拓扑结构中多条边同时发送变化的情况。

Xiao[12-13]先后提出了两个半动态最短路径算法。处理边权值减小的半动态算法（MinD，MaxR）为分支更新算法，处理边权值增大的半动态最短路径算法为点更新算法。并给出了将处理边权值增大的动态最短路径算法改进为分支更新算法的思路。然而，MinD以及MaxR算法中存在错误以及冗余计算。本文将对此进行改进。

1 多链路权值减小算法改进

MinD以及MaxR算法具有相同的算法框架，不同的仅仅是出队方式。因此本文的改进对MinD以及MaxR算法均有效。

1.1 Nfixed（v）定义改进

在XiaoBin链路权值减小算法中，Nfixed（v）为一节点集合保证了算法节点更新范围的正确性。Nfixed（v）在MinD以及MaxR算法中的定义和用法完全相同。根据算法对Nfixed（v）的用法，Nfixed（v）的定义存在错误。

在原算法中，Nfixed（v）的定义如下所示：对给定的节点及其路径值的增量，首先将其加入Nfixed（v），节点加入如果满足下面2个条件：

（1）P(v')∈Nfixed(v) ；（2）vv′'∉MM or v'∈M but M.v'.d1=0 and M.v'.d1≥d

条件1表明等待加入的节点必须为子节点；条件2表明其他边权值减小，但是增量大于 节点的增量。按照上面的定义进行更新将存在错误，如图1所示。

图1 多链路权值减小

图1中两条边权值减小，分别是(S,A)和(B,C),初始化后，队列M中有两个元素{A，(-8,0,0)}以及{C，(0,B,-2)}。首先处理边{A，(-8,0,0)}，C节点应加入Nfixed(A)，因为初始化边(B,C),时，加入队列M的元素为{C，(0,B,-2)},而A节点的更新量为-8，从而C节点加入Nfixed(A)并将{C，(0,B,-2)}从M中删除。此时边(B,C),的变化将不会更新SPT。从而，S到C的最短路径将是S→A→C, 最短路径的值为8。而路径S→A→B→C的值为6，存在错误。出错的原因，为B节点为A节点的子节点，父节点所进行的更新子节点会继承。因此，不能简单地删除(B,C)的变化，提出的改进措施是将第2个条件进行修改：

当子节点在M中并且增量大于d时，且潜在的父节点为v的子孙节点时，将不被加入Nfixed(v)，以免产生错误的更新。

1.2 边的改进

在XiaoBin算法中，检查更新节点是否可更新非Nfixed(v)节点时，将边权值的变大和减小分开处理，des（v）中的节点如果不在Nfixed(v)中，则可分为两种情况：要么在M中，要么不在M中。对于第二类节点，可知在算法33行检查时，d'≥d恒成立。另一方面之所以此节点未加入Nfixed(v)，一定是由于其某父节点的增量小于d。且因为继承关系，此种类型的节点被加入队列M后还没有更新SPT就被删除，即此加入操作为无效的。此种类型的情况如图2所示。

图2 节点检查

由图2可见，在进行初始化之后，M={{B，(-5,0,0)}，{D，（0,C,-6)}}。算法第2步取出{B，(-5,0,0)},由于-6＜-5，节点Ev′∉MNfixed(B),Nfixed(B)={B}。从而在边检查时，将加入{E，(0,B,-4)}。而在取出{D，(0,C,-6)}更新时将删除{E，(0,B,-4)},从而在{E，(0,B,-4)}中加入操作、删除操作以及维护操作均是无效的。因此，将边检查的范围改为：

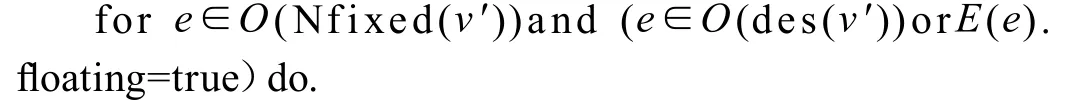
这样可减小一部分无效的入队出队操作。

2 仿真验证

本文仿真将比较改进后的MinD算法以及Dijkstra算法以验证改进算法的准确性。

2.1 拓扑结构的产生

初始拓扑结构由Inet3.0软件[14]构成，Inet软件生成的拓扑结构不仅可以保证连通性，还符合Internet经过验证的幂律特性。Inet 3.0产生的拓扑结构由点和边构成。全部节点均分布在长和宽均为10 000的平面内，初始的随机种子数为0。最后得到节点数为5 000，无向边为8 901（有向边17 802）的拓扑结构。由于产生的拓扑结构比较复杂，在本文中此拓扑结构将不以图形的方式展现出来。

2.2 事件的产生

变化的拓扑结构由系统的随机接口函数来实现。由于拓扑变化可视为边权值的变化，因此文中的拓扑变化均用边权值的变化代替。用Inet 3.0生成的边的顺序进行编号，用随机数对边拓扑求余，以确定变化拓扑的顺序编号。Inet 3.0构成的边拓扑没有方向，所以使用随机数十位上的奇偶性确定边的方向。十位数为奇数时，边的方向即为边拓扑自身的方向，否则，则相反。拓扑变化的方向即权值增大或是减小通过随机数的奇偶性确定，为奇数时，则边权值变大，为偶数时，则边权值变小。由于随机数的个位数和十位数相互独立，保证了变化拓扑方向与拓扑变化方向的独立性。拓扑变化总量则用另一个随机数确定。边权值的变化量则用边拓扑自身的权值为上界，以保证拓扑变化后其权值为非负的性质。

2.3 仿真结果

根据生成的拓扑及变化拓扑，由Dijkstra算法与改进后的算法比较以验证改进算法的正确性；比较边检查改进前后算法的入队次数情况。结果如表1所示。

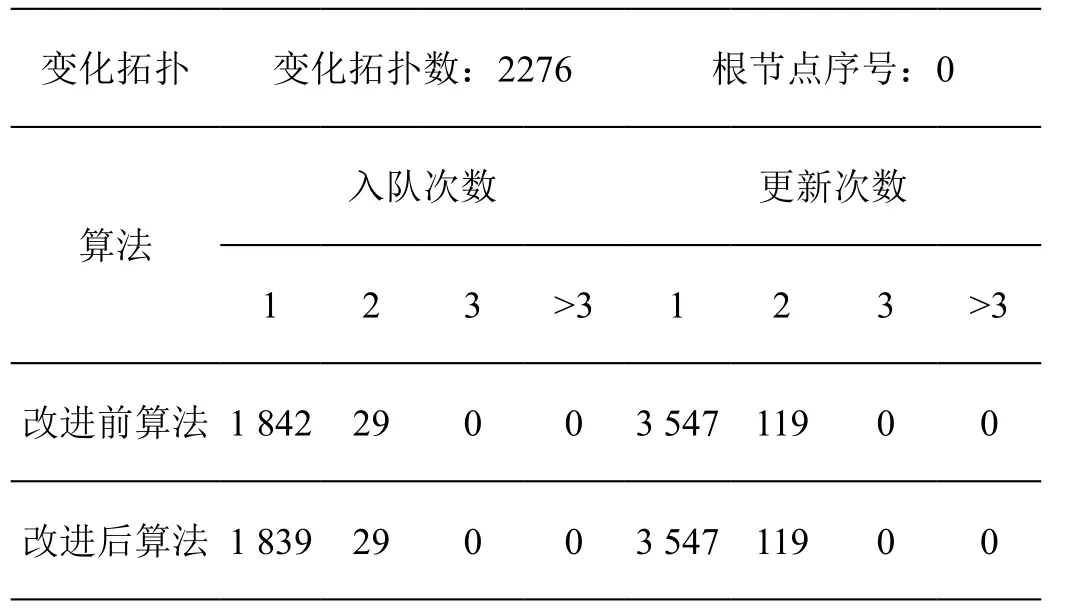
表1 仿真结果

与Dijkstra算法的比较结果未在表中给出，根据比较结果，改进后算法是正确的。从表1的实验统计数据可知边检查的改进减小了节点入队的次数。

3 结语

本文纠正了XiaoBin多链路权值减小的分支更新动态最短路径算法中Nfixed（v）的定义错误，改进了其边检查的方式。仿真结果表明，改进的算法具有正确性，并降低了队列维护的冗余计算。

[1]MOY J. RFC2328: OSPF Version 2[EB/OL].（1998-04-23）[2016-11-22].http://www. ietf. org / rfc/ rfc2328.txt, April 1998.

[2]DAVID O. RFC1142: OSI IS-IS intra-domain routing protocol[EB/OL].（1990-02-11）[2016-11-22].http://datatracker.ietf.org/doc/rfc1142/. [3]EDSGER W D. A note on two problems in connection with graphs[J]. Numerical Math, 1959（1）：269-271.

[4]REINHARD B, DOROTHEA W. Batch dynamic single-source shortest-path algorithms: an experimental study[C].SEA’09 Proceedings of the 8th International Symposium on Experimental Algorithms, Heidelberg：Springer-Verlag, 2009：51-62.

[5]RICHARD B. On A routing problem[J]. Quarterly of Applied Mathematics, 1958（1）：87-90.

[6]KNUTH D E. A generalization of Dijkstra’salgorithm[J]. Information Processing Letters, 1977（1）：1-5.

[7]MCQUILLAN J M, RICHER I, ROSE E C. The new routing algorithm for the Arpanet[J]. IEEE Transactions on Communication, 1980（5）：711-719.

[8]NARVAEZ P, SIU K Y, TZENG H Y. New dynamic algorithms for shortest path tree computation[J]. Transactions on Networking, 2000（6）：734-746.

[9]NARVAEZ P, SIU K Y, TZENG H Y. New dynamic algorithms based on a ball-and-string model[J]. Transactions on Networking, 2001（6）：706-718.

[10]PAOLO G F, DANIELE F, ROBERTO G. Semi-dynamic shortest paths and breadth-first search in digraph[J].Theoretical Aspects of Computer Science, 1997（1200）：33-46.

[11]DANIELE F, MARCHETTI S, NANNI U. Fully dynamic output bounded single source path problem[J]. Algorithms, 2000（2）：251-281.

[12]XIAO BIN, CAO JIANGNONG, ZHUGE QINGFENG, et al. Shortest path tree update for multiple link state decrements[C]. Globecom’04 dallastexas IEEE, 2004：1163-1167.

[13]XIAO BIN, CAO JIANGNONG, SHAO ZILI, et.al. An efficient algorithm for dynamic shortest path tree update in network routing[J]. Journal of Communication and Networks, 2007（4）：409-510.

[14]WINICK J, JAMIN S. Inet-3.0：Internet topology generator[EB/OL].（2002-10-15）[2016-12-10]http：//www.ssat-inet.net/, UM-CSETR- 456-02, 2002.

Study of dynamic SPT algorithm for multi-link decrement

Guo Wenqiang1, Xiao Qiancai2, Li Mingqi2
（1.Computer Science and Engineering College of Xinjiang University of Finance , Urumqi 830012, China; 2.University of Electronic Science and Technology of China, Chengdu 611731, China）

Batch updating algorithms for dynamic shortest path can effectively improve the computing efficiency of shortest path. Through analyzing the current situation and problems of the shortest path algorithm of dynamic, the article improved the definition of Nfixed (V) to solve the edge check redundancy in the original algorithm, and improved MinD algorithm and MaxR edge inspection steps, effectively reduced the times of repeated inspections. The simulation results show that the improved algorithm has higher efficiency.

linear programming; network topology; routing protocols; dynamic shortest path algorithm; dynamic updating algorithm

国家自然科学基金项目；项目编号：61163066，60902074。新疆自然科学基金项目；项目编号：2013211A032。

郭文强（1975— ），男，吉林安图，博士，教授；研究方向：信息安全，信号与信息处理。