云计算中安全技术强化性研究

杨晓静，陈明晰，孙 涛

（西安石油大学 计算机学院，陕西 西安 710065）

云计算中安全技术强化性研究

杨晓静，陈明晰，孙 涛

（西安石油大学 计算机学院，陕西 西安 710065）

云安全中的隐私保护和数据安全是当今的研究焦点，决定了其未来的发展前景。针对云计算安全风险，本研究将椭圆曲线加密技术和高级加密技术高效组合应用于由Hadoop和Cassandra构成的云环境中，在保证数据安全和隐私保护的同时最小化额外开销，为了保护云安全，文章还应用了MATLAB技术进行软件开发。

云计算；云安全；椭圆曲线加密；公钥加密；云存储；MATLAB

云计算是当今最具活力研究领域，它为用户提供各种服务，其中一种重要的服务是云存储。云存储是指用户将大量的私人数据存储在在线的空间。严谨地讲：云存储是一种服务模型，在这种模型中用户通过网络远程保存、处理、备份数据。

借助Hadoop存储数据：Apache Hadoop开发了一个Hadoop应用程序管理云存储。多个数据块的副本被创建和分布中一个集群的多个计算节点上从而加访问算速度。一个横向扩展的架构利用一组被规划服务器确保每个服务器承担更低的内部存取压力。Hadoop数据被分割成块分布在整个集群中。Mapreduce涉及映射和集约两种操作，映射操作输入密钥数据对产生中间的密钥/数据而规约操作将中间密钥数据对划分成更小的数据集合。MapReduce很适合大数据的处理。

1 云计算研究背景

云计算通过一些公有、私有的网络连接很多系统，为应用程序、数据、文件存储提供基础设施，具备可伸缩性和动态性，但是存在大量的安全问题。在公共云中常用的加密技术包括高级加密标准（Advanced Encryption Standard，AES）和椭圆曲线加密（Elliptic Curve Cryptography，ECC）。AES：基于替代和置换网络，是一种对称加密，相同的密约执行加密和解密操作。ECC是一种公钥加密方案基于椭圆曲线离散对数问题的困难性。每个用户拥有公钥和私钥，公钥用于加密和签名验证，私钥用于解密和数字签名生成。

本研究将椭圆曲线加密技术和高级加密技术高效组合应用于由Hadoop和Cassandra构成的云环境中，实现了公共云中实现数据完整性和高等级的安全。对称加密如AES，公钥如ECC。本系统的框图如图1所示。

2 系统开发所用技术

云提供者提供数据存取服务，云用户可以访问和存取数据。在当前的环境中，由于安全等级较低，数据很容易被第三方和匿名用户窃取。在本研究中，为了数据的安全加密技术以一种更有效的方式融入。云存储中加密技术实现数据的完整性验证，无需可信的第三方认证（The Third Party Authentication, TTPA）。使用椭圆曲线加密提高安全性：Diffie-Hellman和ElGamal的安全性取决于有限循环群中的离散对数。用于公钥加密的传统群是Z*p，计算离散对数最常用的方法是指数计算法。RSA加密算法和ElGamal适合于椭圆曲线，各自的变体被称为椭圆曲线。例如2048位密钥的RSA算法的安全性可以达到224位椭圆曲线密钥的安全性。

3 椭圆曲线的设计

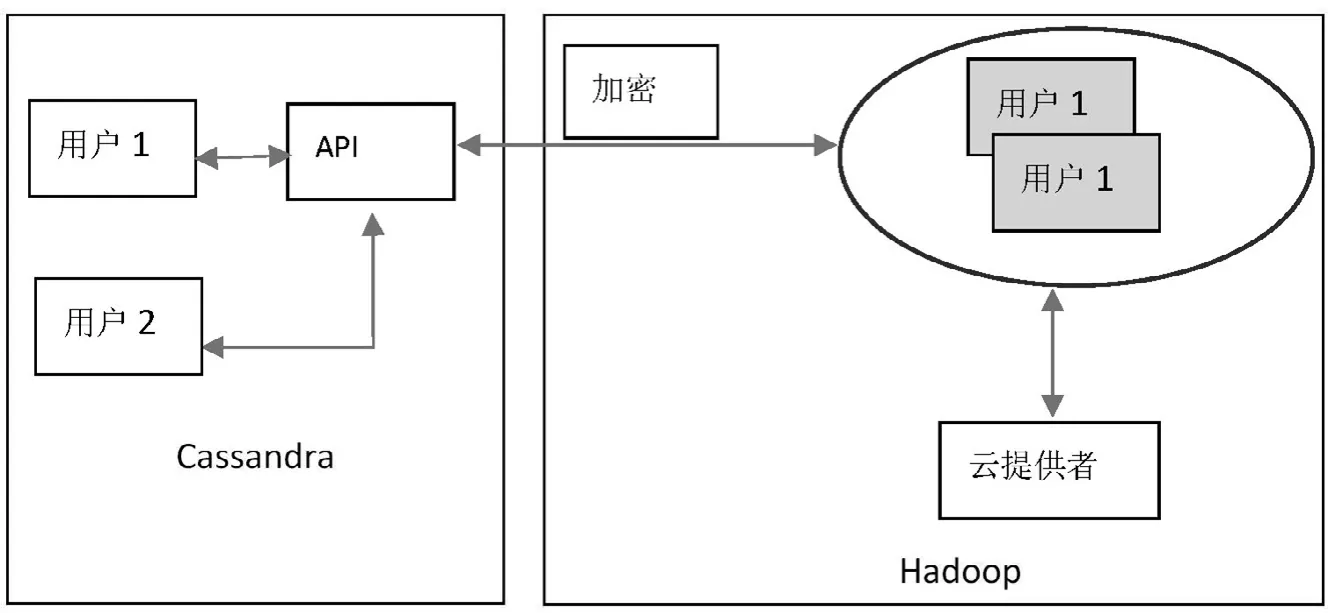
图1 本系统框图

加密系统包括基于Diffie-Hellman算法的椭圆曲线模拟的方案生成密钥和基于ElGamal的椭圆曲线模拟的方案用于加密和解密。

椭圆曲线是一条平面曲线，形式如下：

其中X和Y有限域上的元素。文中用到参数含义：E代表了椭圆曲线，P是曲线上的点，生成了一个n阶的循环子群E。对于循环子群E，生成元P：

={8，2P，3P，…，（n-1）P}

3.1 密钥生成

对应Diffie-Hellman公钥系统，可以通过如下方式在椭圆曲线上予以实现：在E上选取生成元P，要求由P产生的群元素足够多，通信双方A和B分别选取a和b，a和b予以保密，但将aP和bP公开，A和B间通信用的密钥为abP，这是第三者无法得知的。

加密：将明文m嵌入到E上Pm点，选一点B∈E，每一用户都选一整数a，0＜a＜N，N为阶数已知，a保密，aB公开。欲向A送m，可送去下面一对数偶：［kB，Pm+k（aAB）］，k是随机产生的整数。A可以从kB求得k（aAB）。通过：Pm+k（aAB）- k（aAB）=Pm恢复Pm。同样对应DSA，考虑如下等式：

K=kG [其中K，G为Ep（a，b）上的点，k为小于n（n是点G的阶）的整数]

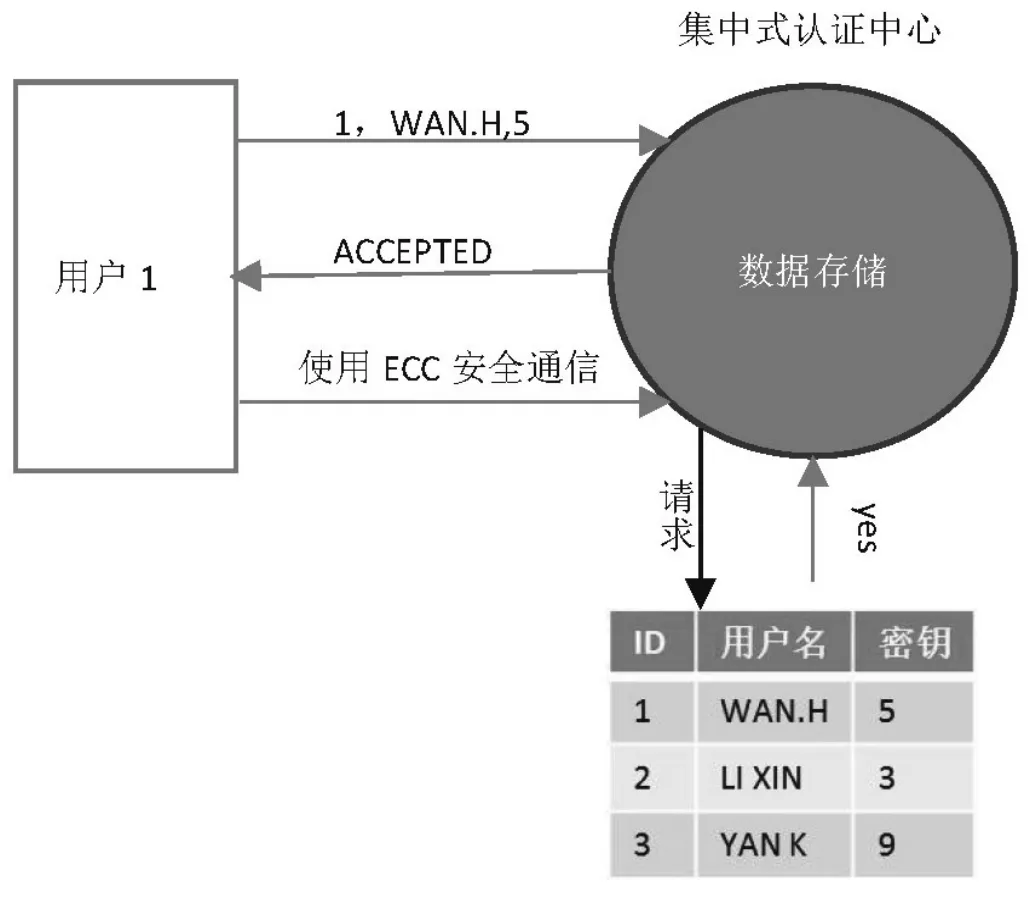
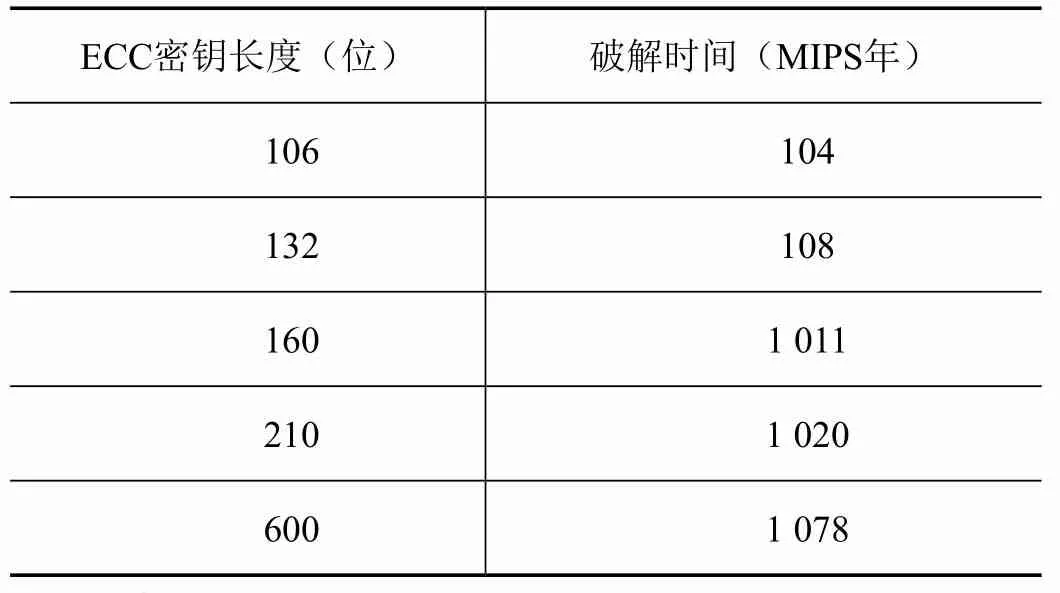
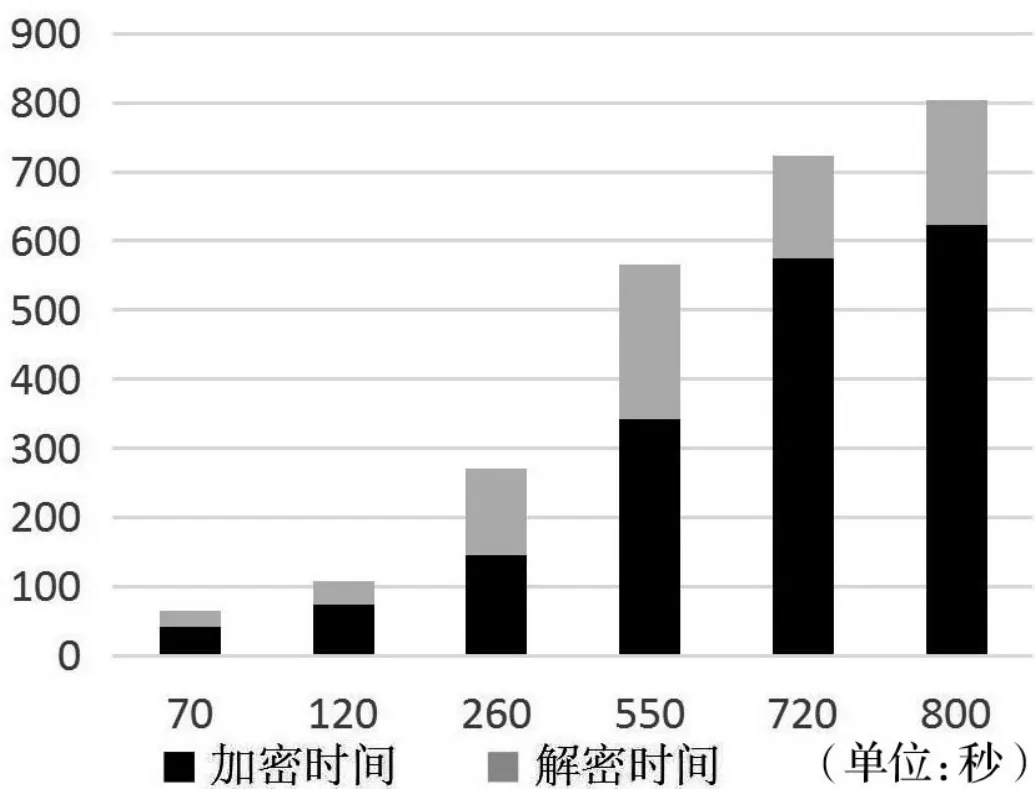
不难发现，给定k和G，根据加法法则，计算K很容易；但给定K和G，求k就相对困难了。点G称为基点（base point），k（k

使用ECC，不同的会话分享不同的密钥，因此入侵者不可能追踪数据。因此安全性能高且密钥发散问题得到保证。

3.2 设计实现

云系统中安全传输，利用Hadoop工具初始化云存储器（例如超过1T的数据。当用户1访问存储在云环境中的数据，需要发送用户凭证（用户名，id，密钥）。

图2描述了应用AES技术完成身份验证。应用Cassandra工具，创建授权数据库保存ID，用户名和密钥。

图2 使用AES技术技能型加密认证

用户1希望访问存储在Hadoop中的信息，集中式认证中心验证数据库中用户身份凭证。如果用户的身份凭证和授权数据库中的信息匹配，如图3所示，给集中式认真中心反馈”yes”。集中式认证中心接受用户访问数据。

图3 表示应用Cassandra工具创建授权数据库

图4描述一旦认证成功，应用ECC加密在用户和集中式认证中心之间传送的信息。图5显示，一旦认证不成功，应用ECC通信将被拒绝。

图4 应用ECC安全通信

图5 拒绝黑客

表1描述了应用ECC对不同长度的数据加密和解密时间，图6描述了加密时间和解密时间的关系。

表1 应用ECC对不同长度的数据加密和解密时间

4 结语

在由Hadoop和Cassandra组成云环境中。通过使用AES技术在用户和授权数据库之间认证用户真实身份。一旦认证成功，使用椭圆曲线加密在技术在用户和认证中心之间通信。这种加密方案强化数据安全性、保护用户隐私，但同时安全开销较小。实际应用也证实这是一种高效安全的加密方案。

图6 加密时间与解密时间关系

[1] DEVI D, ARUN P S.A Design for secure data sharing in cloud[J].International Journal of Engineering Research and General Science, 2014（5）：72-77.

[2]XIAO C Y, ZENG G L, HOON J L.An Efficient and Secured Data Storage Scheme in Cloud Computing Using ECC-based PKI[J]. International Conference on Applied Chemistry and Chemical Engineering，2014（10）：523-527.

[3]POOJA H P, NAGARATHNA N. Privacy Preserving Issues and their Solutions in Cloud Computing[J].International Journal of Computer Science and Information Technology, 2014（2）：1588-1592.

[4]洪澄，张敏，冯登国. AB-ACCS：一种云存储密文访问控制方法[J].计算机研究与发展，2010（Z1）：47.

Research on security strengthening property of technology in cloud computing

Yang Xiaojing, Chen Mingxi, Sun Tao
（Computer Science College of Xi’an Shiyou University, Xi’an 710065, China）

Privacy protection and data security in the cloud security is the focus of today’s research, to determine its future development prospects. Based on cloud computing security risk, this study applied elliptic curve encryption technology and advanced encryption technology efficient combination to the in the cloud environment composed of Hadoop and Cassandra, to ensure data security and privacy protection while minimizing the overhead, in order to protect the security of cloud, the application of the MATLAB technology is carried on the software development.

cloud computing; cloud security; elliptic curve cryptography; public key encryption; cloud storage; MATLAB

杨晓静（1972— ），男，陕西西安；研究方向：云计算，网络安全。