离心风机切割定律的研究和探讨
唐照付 金守清 朱如洪 李品善/上海诺地乐通用设备制造有限公司
离心风机切割定律的研究和探讨
唐照付 金守清 朱如洪 李品善/上海诺地乐通用设备制造有限公司
本文在风机相似定律的基础上推导出离心风机的切割定律计算公式。通过试验和CFD对几种风机进行叶轮切割研究,给出了比转速为~14的离心风机修正系数k与切割量占比的线性关系,对离心风机叶轮切割后性能推算具有指导意义。
离心风机;切割定律;叶轮;CFD
0 引言
离心风机的应用范畴非常广泛,在实际使用时由于选型或设计的原因,经常出现设计性能与实际需要的性能或多或少存在一些偏差,一般的方法有通过调节转速、管路系统配置调节风阀等来调节风机运行性能。离心风机直联驱动相对皮带驱动易损件少、更可靠,但由于直联时受转速限制,性能比较固定,配置变频器又增加了设备成本,这样就限制了直联风机的选型空间。一般风机生产厂家都是按系列化标准化生产的,当遇到风机性能不满足客户需求时,需要进行非标设计,但往往设计不精确,开发周期长费时费力。由于离心风机切割定律的文献报道极少,借鉴离心泵的切割定律[1-2],本文旨在探讨离心风机叶轮切割对性能的影响规律,希望能为风机相关工程技术人员在非标叶轮设计及现有风机改造设计方面提供一些参考。
1 离心风机切割公式推导
叶轮切割就是将叶轮外缘车掉一部分,往往需要切割的量不是很多,否则性能改变过大,严重影响效率。当叶轮切割量很小时,叶片出口宽度和出口安装角变化都不是很大,在一定程度上满足风机相似定律,但需要对相似定律进行修正即得到切割定律。
风机相似定律[3-4]:
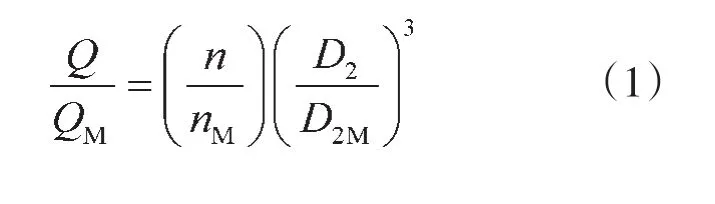
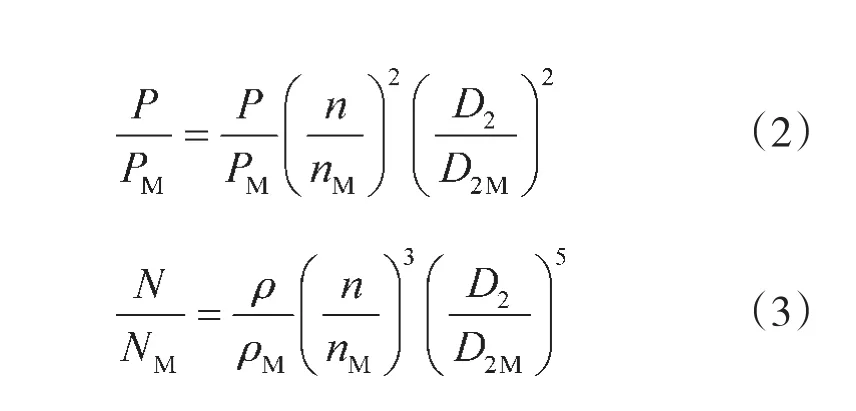
相同转速相同进气条件下的相似定律为:
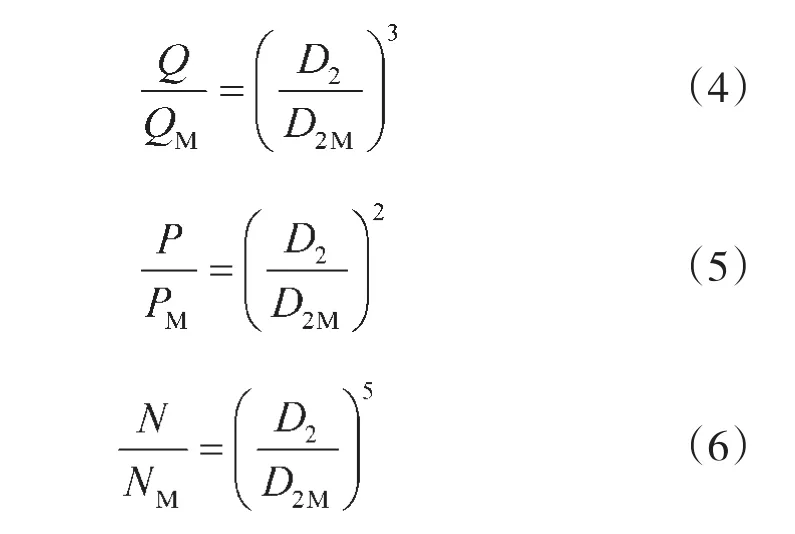
为了使风机的相似定律更加精确地应用于切割后的性能推算,这里引入修正系数K,则切割量:
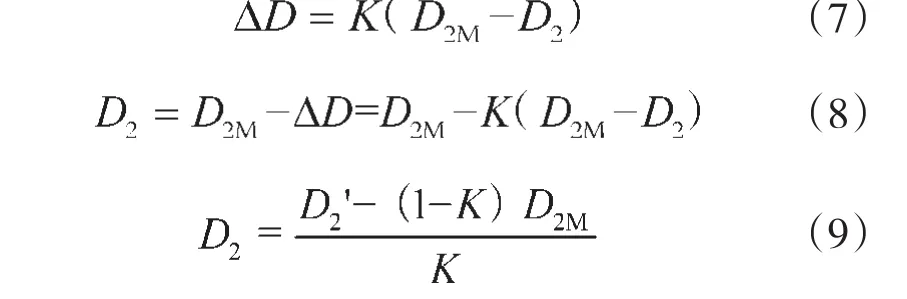
将式(9)带入式(4)~(6)得修正后的相似定律即切割公式:
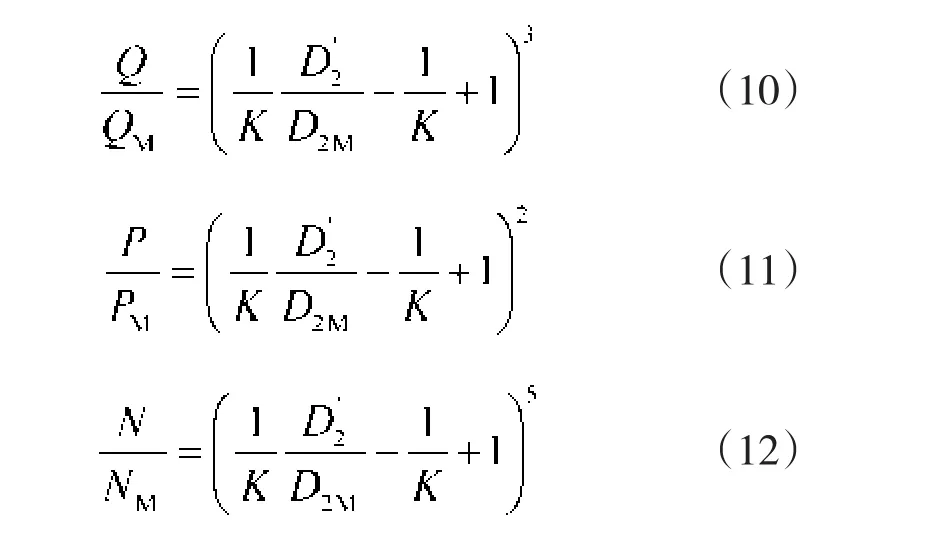
式中,Q,P,N,D2为利用相似定律计算时的设计变量;QM,PM,NM,D2M为模型变量;D2'为利用切割公式计算时的设计变量。
这里,由于切割量越多或切割后叶片出口宽度及出口安装角变化越大,切割定律相对相似定律误差越大,修正系数K就越大,下面将借助试验和CFD数值模拟来探讨K值。
2 试验研究
利用本公司现有条件,选取一台箱式离心风机进行试验。风机原型及切割后尺寸如表1所示。
1#、2#和3#风机实际测试结果(试验平台为上海诺地乐通用设备制造有限公司AMCA国际认证的空气动力性能实验室,测试方法为A型风室进气试验)[5]如图1所示。

表1 不同切割占比对应的叶轮尺寸参数表
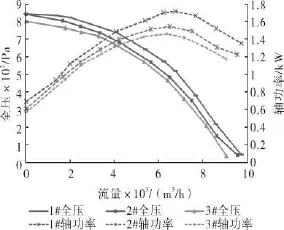
图1 叶轮不同切割占比性能对比图
2#风机实测数据和1#风机相似换算数据及1#风机切割定律推导数据对比如图2所示。
3#风机实测数据和1#风机相似换算数据及1#风机切割定律推导数据对比如图3所示。
据图2和图3可知,叶轮切割后实测性能与用相似定律推导的数据存在较大误差,相似定律推导的数据偏小,切割量越多,误差越大;而修正后的相似定律即切割定律计算出的数据与实测数据吻合很好,这里所选的修正系数K值2#风机为1.1,3#风机为1.25,可见切割量越多修正系数越大。由于试验条件限制,为了得到K值的普遍选取规律,下面将借助CFD这一经济可行的方法对其进行研究。
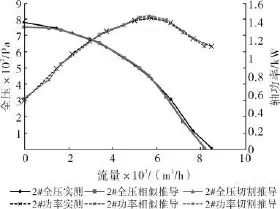
图2 2#风机性能切割与相似对比图
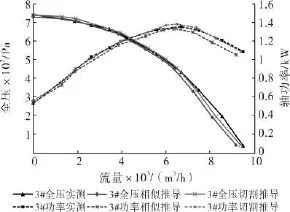
图3 3#风机性能切割与相似对比图
3 CFD数值模拟对K值选取的研究
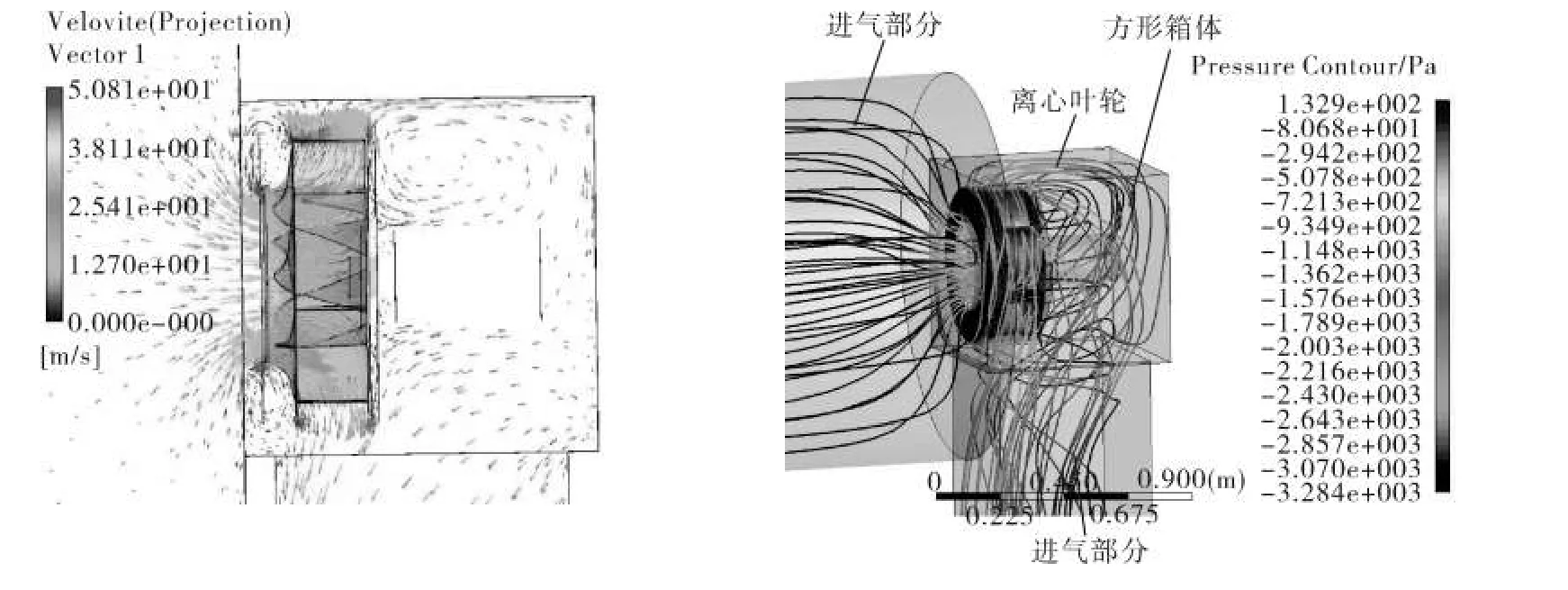
图4 箱式风机流场图
为了验证所选计算方法的可靠性,将上述箱式离心风机的CFD计算结果与实测结果进行了对比。数值模拟所选软件CFX,风机模型及流场分布见图4。模拟采用四面体网格,边界层inflation设置3层,cell单元数525万,分析类型为三维稳态不可压缩,湍流模型SST,动静子交界面interface Models:General Connection,坐标系变换或混合模型选Frozen Rotor即冻结转子法,Pitch Change选None,Mesh Connection选GGI,壁面函数选自动Automatic。求解器对流项选迎风格式Upwind,湍流计算采用高阶算法High Resolution。边界条件为速度进口,自由出口,叶轮壁面无滑移旋转,其余壁面为静止[6]。CFD计算结果与实测数据对比见图5。
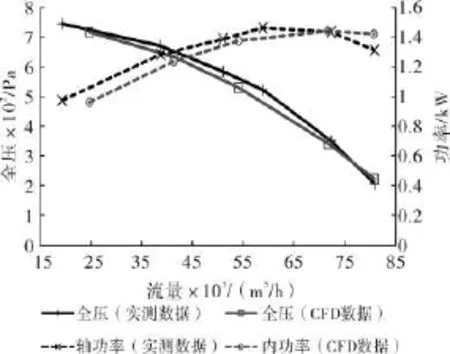
图5 CFD计算结果与实测数据对比图
如图5对比可知所选CFD计算方法得到的数据与实测数据吻合较好,全压最大误差4.5%;功率最大误差5.5%,实测功率是轴功率,CFD所计算功率为空气功率即内功率,所以两者误差较大一些。说明该CFD方法具有一定参考意义。故在此基础上,计算了另外两种型号的风机(如表2),并对叶轮进行一定量的切割。
风机一切割后CFD数据与用切割前CFD数据进行切割定律推算后的数据对比见图6。
风机二切割后CFD数据与用切割前CFD数据进行切割定律推算后的数据对比见图7。
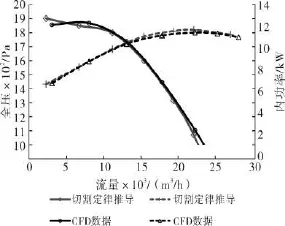
图6 风机一CFD数据与切割定律推导数据对比图
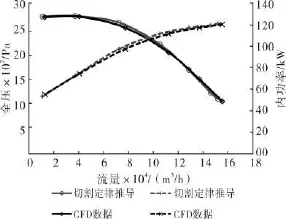
图7 风机二CFD数据与切割定律推导数据对比图
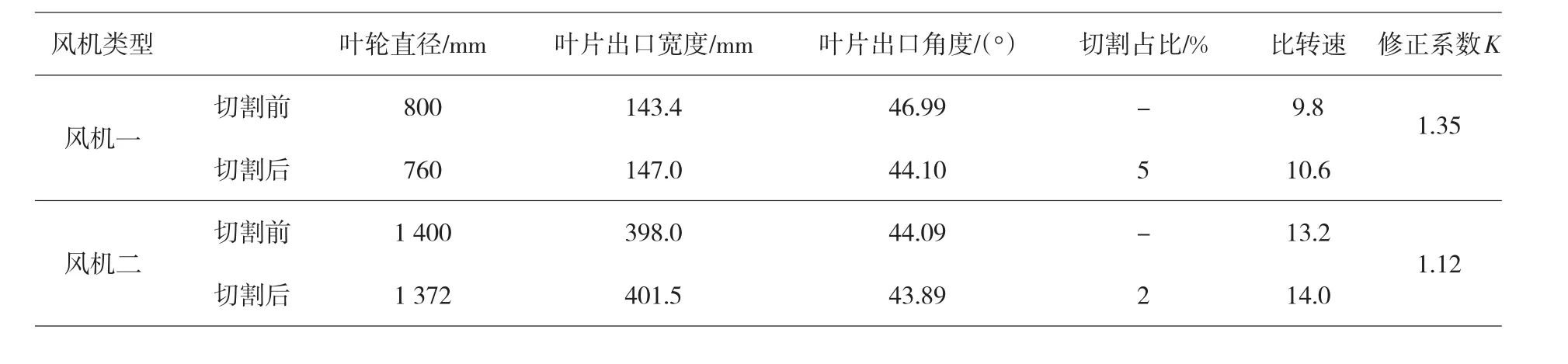
表2 不同风机切割修正系数表
综合上述各风机修正系数K值和切割占比的关系,拟合成如图8所示的曲线。经过我公司比转速为9~14其他型号风机切割定律的CFD验证,图8所示修正系数K值与切割占比的关系吻合很好,这里不再赘述性能的对比情况。
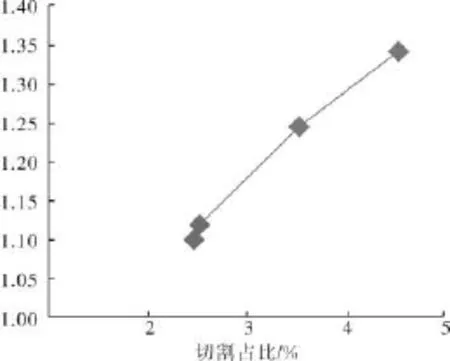
图8 修正系数K值与切割占比的关系图
4 结论
1)根据风机相似定律推导出修正后的离心风机相似定律,即切割定律公式。
2)修正系数K值与切割量(切割占比)有关,切割占比越大K值越大。当比转速在9~14之间时,K值与切割量占比基本成正相关,修正系数K与切割占比的关系曲线见图8。
3)由于本文研究的离心风机种类较少,试验数据不充足,本文提出的K与切割占比的规律仅供与本文相近类型风机和比转速为7~14的离心风机参考使用。K值的普遍规律以期后续研究完善。
[1]关醒凡.泵的理论与设计[M].北京:机械工业出版社,1987.
[2]关醒凡.现代泵理论与设计[M].中国宇航出版社,2011.
[3]李庆宜.通风机[M].北京:机械工业出版社,1981.
[4]徐忠.离心式压缩机原理[M].北京:机械工业出版社,1990.
[5]ANSI/AMCA 210-07.Laboratory Methods of Testing Fans for Certified Aerodynamic Performance Rating,2007.
[6]丁源,吴继华.ANSYS CFX 14.0从入门到精通[M].北京:清华大学出版社,2013.
ResearchandDiscussionon Cutting-downLawfor Centrifugal Fans
Tang Zhao-fu,Jin Shou-qing,Zhu Ru-hong, LiPin-shan/ShanghaiNautilusGeneral Equipment Manufacturing Co.,Ltd
The cutting law for centrifugal fansisdeducedbasedonsimilarity betweenlawsoffansinthispaper. Through research on impeller cutting on several kinds of fan by experiment and CFD methods,the relation of correction factor k is linear to cutting value for centrifugal fans with rotation speeds of 9~14.This offers some guidance for deducing centrifugal fan performance after cutting the impeller.
centrifugal fan;cutting-down law;impeller;CFD
TH432;TK05
A
1006-8155(2016)02-0066-04
10.16492/j.fjjs.2016.02.0060
2015-10-28上海201806

