开关磁阻电机的模糊分数阶PID控制算法研究*

陈超波，邢迪，杨雪辉，张彬彬

（1.西安工业大学，西安710021；2.山东航天电子技术研究所，山东烟台264670）

0 引 言

开关磁阻电机因其结构简单、控制灵活、运行效率高、适于高速与恶劣环境运行，被广泛应用于矿用拖动等场合［1］。由于开关磁阻电机具有双凸极机械结构和开关特性，需长时间运行在饱和状态下，以获得最大输出转矩，导致其电磁特性表现出高度的非线性，将常规PID控制算法用于其转速控制时，由于整个控制系统的结构和参数都是变化的，固定参数的PID调节器难以得到理想的控制性能指标，存在转矩脉动大、力矩不平滑的缺点，进而限制了其在高精度调速场合的应用。为此越来越多的学者开始研究智能控制算法在开关磁阻电机控制中的应用。

文献［2］中对开关磁阻电机控制时，应用具有自学习和自适应能力的神经元构成单神经元自适应控制器，通过RBF网络对系统进行在线辨识，及时调整控制器参数，实验结果表明，该算法具有控制精度高，动态性能好，有较好的自适应性的优点，然而，计算量较大、步骤繁琐使得该算法不能被广泛应用。文献［3］使用模糊控制与单神经元PID相结合的控制算法，其仿真结果表明，该算法具有良好的动静态性能，抗干扰性能也优于传统PID控制算法，但其存在控制精度不高的不足。文献［4］将迭代学习控制引入开关磁阻电机的转矩控制中，通过反复迭代修正控制参数，达到抑制开关磁阻电机转矩脉动的目的，但是该方法运算效率较低，只能适用于低转速情况下。文献［5］对开关磁阻电机的调速控制时，使用电流双幅值斩波控制方法，结果表明该算法达到了低速时降低噪声的目的，但是该方法对转矩脉动的抑制效果十分有限。

针对开关磁阻电机调速系统的强耦合、非线性和不确定性的特点。利用分数阶PID控制算法结构灵活、鲁棒性强的优点，以及模糊算法自适应的优点［6］，文中采用分数阶PID控制和模糊控制相结合的控制算法。根据实际的工程开发经验，建立模糊推理表，以转速偏差和偏差变化率作为模糊控制器的输入，通过模糊推理改变分数阶PID控制器的比例系数，积分阶次和微分阶次，用于开关磁阻电机的转速控制。

1 开关磁阻电机数学模型

开关磁阻电机的工作原理和步进电机的原理相同，即通过给定子一定的电脉冲，根据磁阻最小路径原理，转子将会转动。根据电路基本定理，开关磁阻每相的公式为：

式中uk为第k相电机绕组电压；R为第k相绕组电阻；ik为第k相绕组电流；ψk为第k相磁链。

对开关磁阻电机进行数学建模时，忽略每相的互感特性，则磁链的表达式如式（2）所示。

式中Lk为等效电感，它是转子θ和定子的夹角和定子电流ik的函数，为简化数学运算，其数学模型的示意图如图1所示，图中横轴表示转子位置角θ，纵轴表示等效电感L。由图可知，等效电感值是转子和定子夹角的函数，其函数分布为等腰梯形分布。

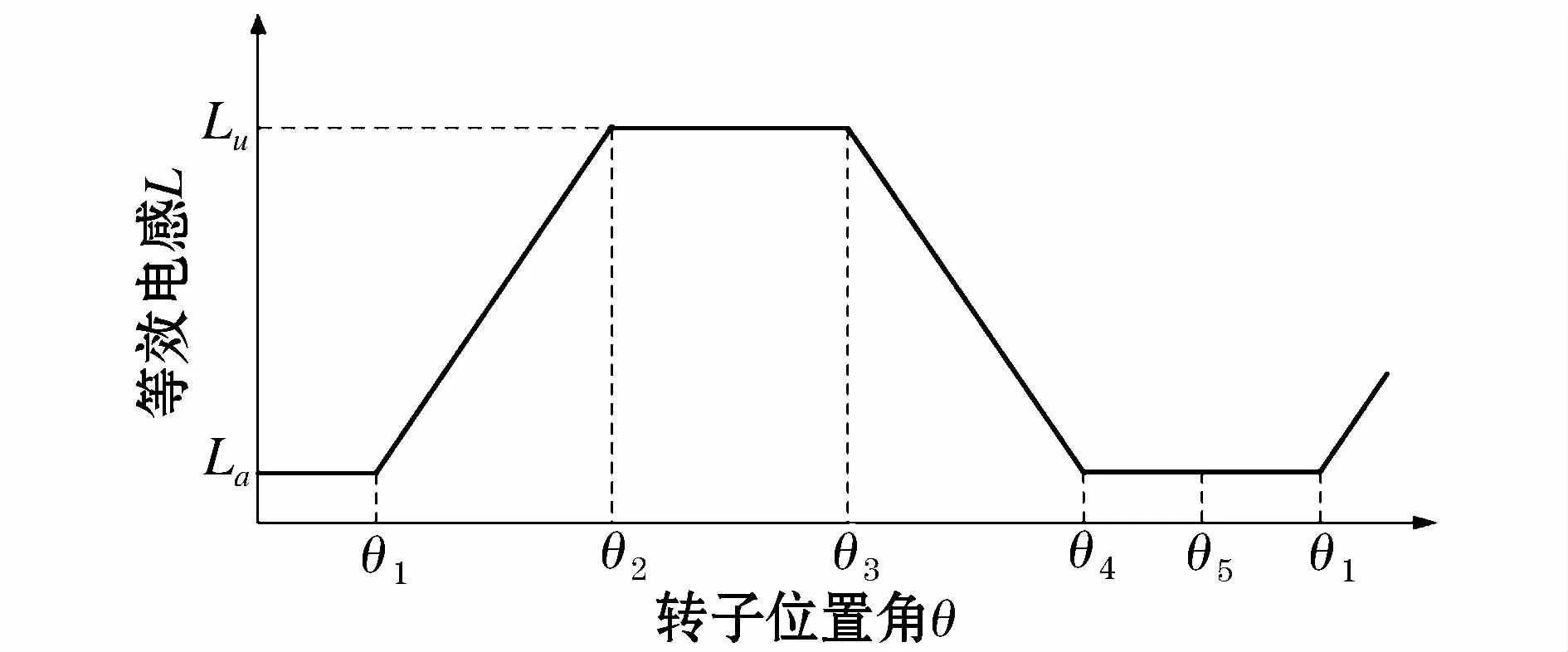
图1 等效电感数学模型示意图Fig.1 A mathematicalmodel schematic diagram of the equivalent inductance

而开关磁阻电机的机电方程如式（3）与式（4）所示。

式中J为电机的转动惯量；Te为电机的电磁转矩；TL为电机的负载转矩。W为磁共能，其中开关磁阻电机为k相电机。

由于等效电感的数学模型为非线性函数，故整个开关磁阻电机的数学模型具有非线性、时变性的特点。将常规线性控制算法应用于开关磁阻电机调速系统中时，存在转矩脉动较大的问题。

2 模糊分数阶PID算法

2.1 分数阶PID算法

分数阶微积分至今没有统一的数学定义，目前应用广泛的有三种分数阶定义［7］，文中选择 GL（Grünwald-Letnikov）分数阶微积分定义：

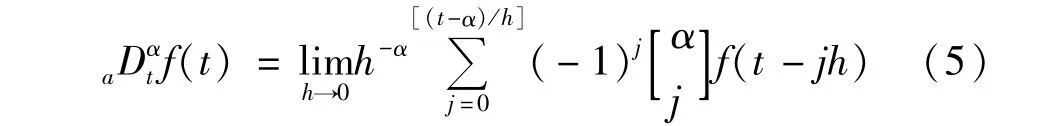
分数阶PID控制器的传递函数如式（6）所示：

和整数阶PID类似，式中KP为比例系数；KI为积分系数；KD为微分系数；λ为积分阶次；μ为微分阶次。

根据GL分数阶微积分定义对式6进行离散化［7］，则分数阶PID的数值表达式如式（7）所示。

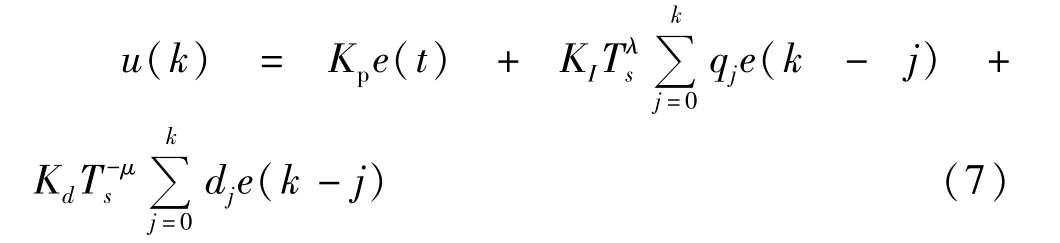
式中TS为采样时间；qj，dj为二项式系数，其中q0=u（k）为控制器输出，e（k）为偏差。

增量式分数阶PID算法的公式如式（8）所示：

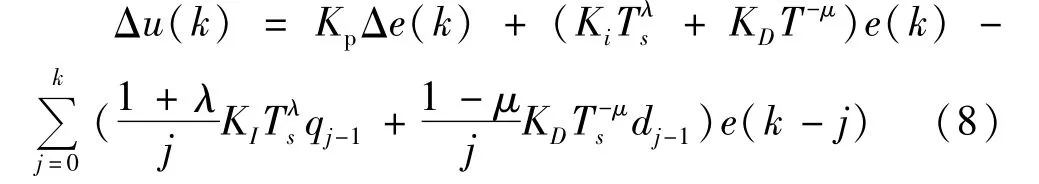
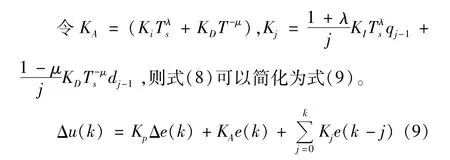
式（9）和经典增量式PID算法比较，多了微分阶次μ、积分阶次λ，对历史的记忆程度更高。为此合理的选择参数，分数阶PID算法将具有较好的鲁棒性。

2.2 模糊分数阶PID算法

文献［8］中，通过对比例系数KP，积分系数KI，和微分系数KD进行模糊推理，调节不同环节的权重，完成模糊分数阶PID控制算法。本文选择对比例系数KP，积分阶次λ和微分阶次μ进行模糊推理，实现模糊分数阶PID控制算法。其工作原理如图2所示。以偏差和偏差的变化率作为模糊推理器的输入，模糊推理器的输出为比例系数、积分阶次和微分阶次，通过将这三个参数传递给分数阶PID控制器，进而控制被控对象。

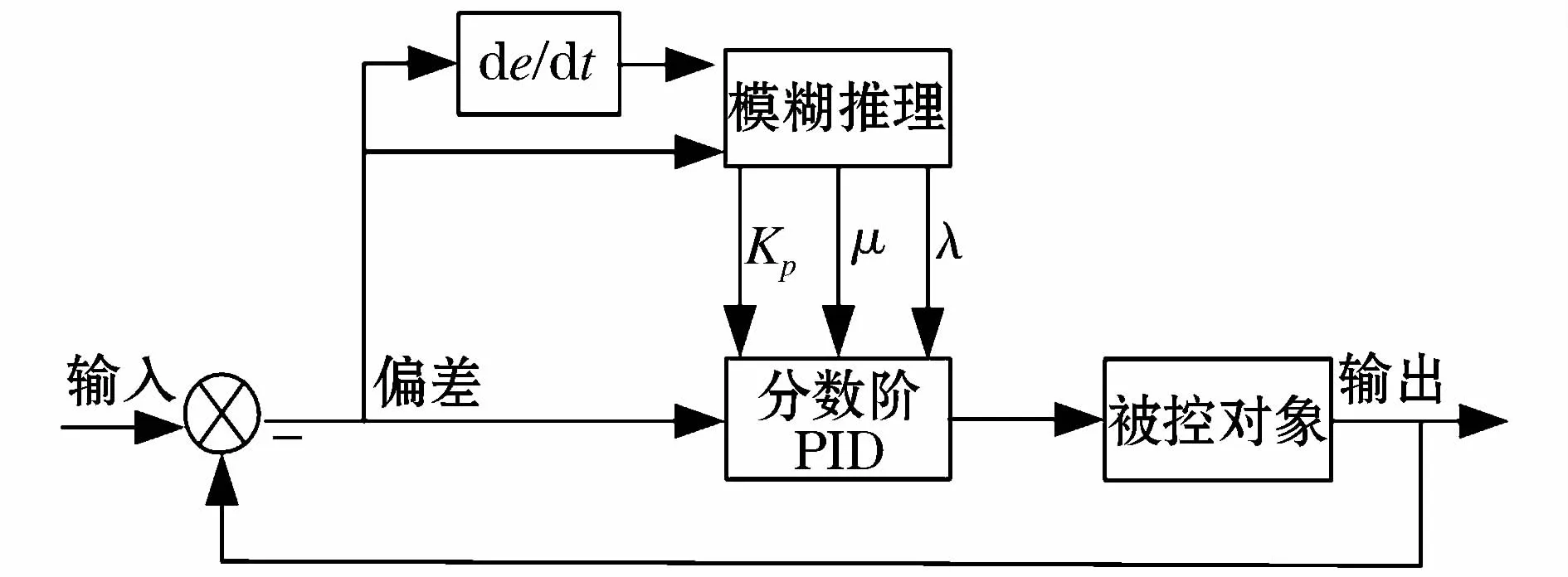
图2 模糊分数阶PID控制原理图Fig.2 Principle diagram of fuzzy fractional PID control

根据文献［9］和分数阶PID控制器在频域方面的分析结论［10-12］可以得知：当KP越大，系统的调节时间越短，反应越灵敏，但是过大的KP会导致系统超调量过大，甚至出现震荡。若积分阶次λ在一定范围（通常为0到2）之内，λ越小，系统的超调越小，静差越大，过大的λ虽然会降低静差，但会导致系统有较大的滞后，甚至会出现震荡。微分阶次μ过大，会使超调减小，同时对系统的噪声也会非常敏感。结合三者对系统的影响，以偏差和偏差的变化率为输入，设计合适的模糊规则，最后完成模糊分数阶PID控制算法。

根据开关磁阻电机调速系统的实际特点，本文确定偏差e和偏差变化率Δe的隶属度函数如图3所示，偏差e和Δe偏差变化率的论域都为{负大，负中，负小，零，正小，正中，正大}用字母表示为{NB，NM，NS，ZO，PS，PM，PB}。

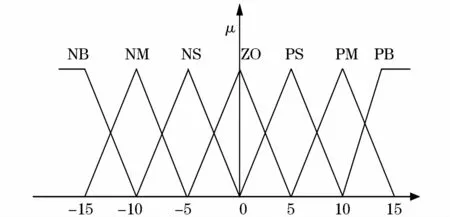
图3 偏差和偏差变化率的隶属度函数Fig.3 Membership functions of the deviation and the deviation rate

文中的模糊推理器的输出量有三个，分别为ΔKP、Δλ和Δμ。为了调试方便，本文使用归一化处理，即输出量为原来量的百分比。三者的隶属度函数如图 4所示，它们的论域为{NB，NM，ZO，PM，PB}，分别表示负大、负中、零、正中、正大。

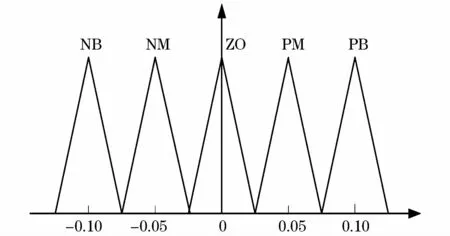
图4 ΔK P、Δλ和Δμ的隶属度函数Fig.4 Membership functions ofΔK P、ΔλandΔμ

确定控制器的输入变量和输出变量的隶属度函数，根据经验控制，可以确定其模糊规则。文中ΔKP、Δλ、Δμ、偏差e和偏差变化率Δe的模糊规则表如表1～表3所示。

表1 ΔK P的模糊规则表Tab.1 Fuzzy rule table of theΔK P

表2 Δλ的模糊规则表Tab.2 Fuzzy rule table of theΔλ

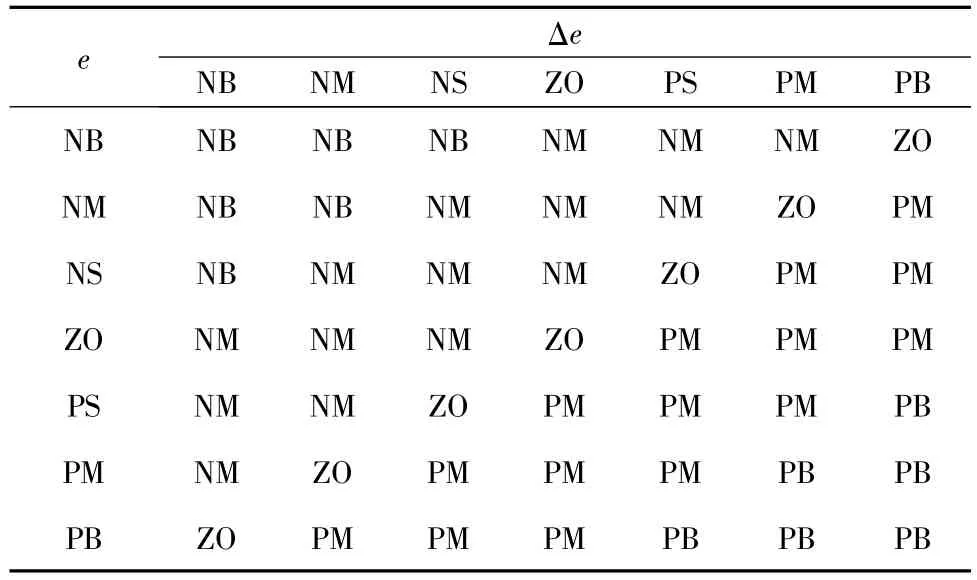
表3 Δμ的模糊规则表Tab.3 Fuzzy rule table of theΔμ

对于解模糊化，文中算法和经典模糊算法一致，在此不作过多解释。本文的算法过程如下：

（1）初始化各个参数。比例系数、积分系数和微分系数的初始值通过常规PID整定算法来整定。积分阶次和微分阶次先设为1；

（2）系统开始运行，得到系统的偏差e和偏差变化率 Δe，通过模糊推理，得到 ΔKP、Δλ和 Δμ；

（3）根据式（8），得到分数阶PID的输出。最后，跳到第2步。

3 仿真结果分析

文中的被控对象为开关磁阻电机，其功率为4 kW，额定电流为25 A，额定电压为110 V，转动惯量为0.002 kG·M2，饱和电感为3 500μH，非饱和电感为300μH，定子回路电阻为100。比例系数、积分系数和微分系数通过常规PID算法整定；分数阶PID算法的参数以常规PID算法的参数为基础，对积分阶次和微分阶次进行整定，其参数为 KP=8.7，KI=0.4，KD=0.06，λ=0.7，μ=0.9；模糊分数阶 PID控制算法的初始参数以分数阶PID算法的参数为基础，采用模糊规则对KP、λ和μ进行自整定。在Matlab中验证三种算法在开关磁阻电机调速系统中阶跃响应，结果如图5所示。

图5 三种算法的阶跃响应对比Fig.5 Step response comparison of the three algorithms

分析图5可知，本文中的模糊分数阶算法的超调量低于常规PID算法和分数阶PID算法，并且调节时间小。为进一步说明本算法的有效性，本文使用控制系统的评价指标评价两种算法的控制效果，结果如表4所示。

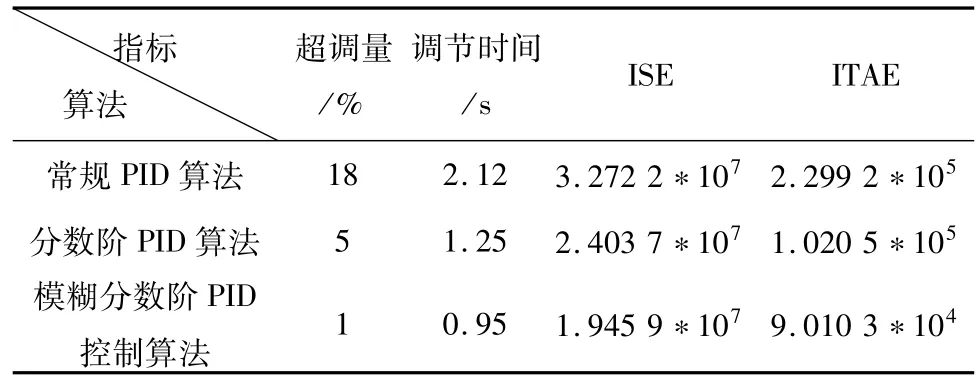
表4 三种算法的控制效果对比Tab.4 Control effect comparison of the threealgorithms

由表4可以看出模糊分数阶PID控制算法的超调量、调节时间等指标均优于其他两种算法，控制效果较好。

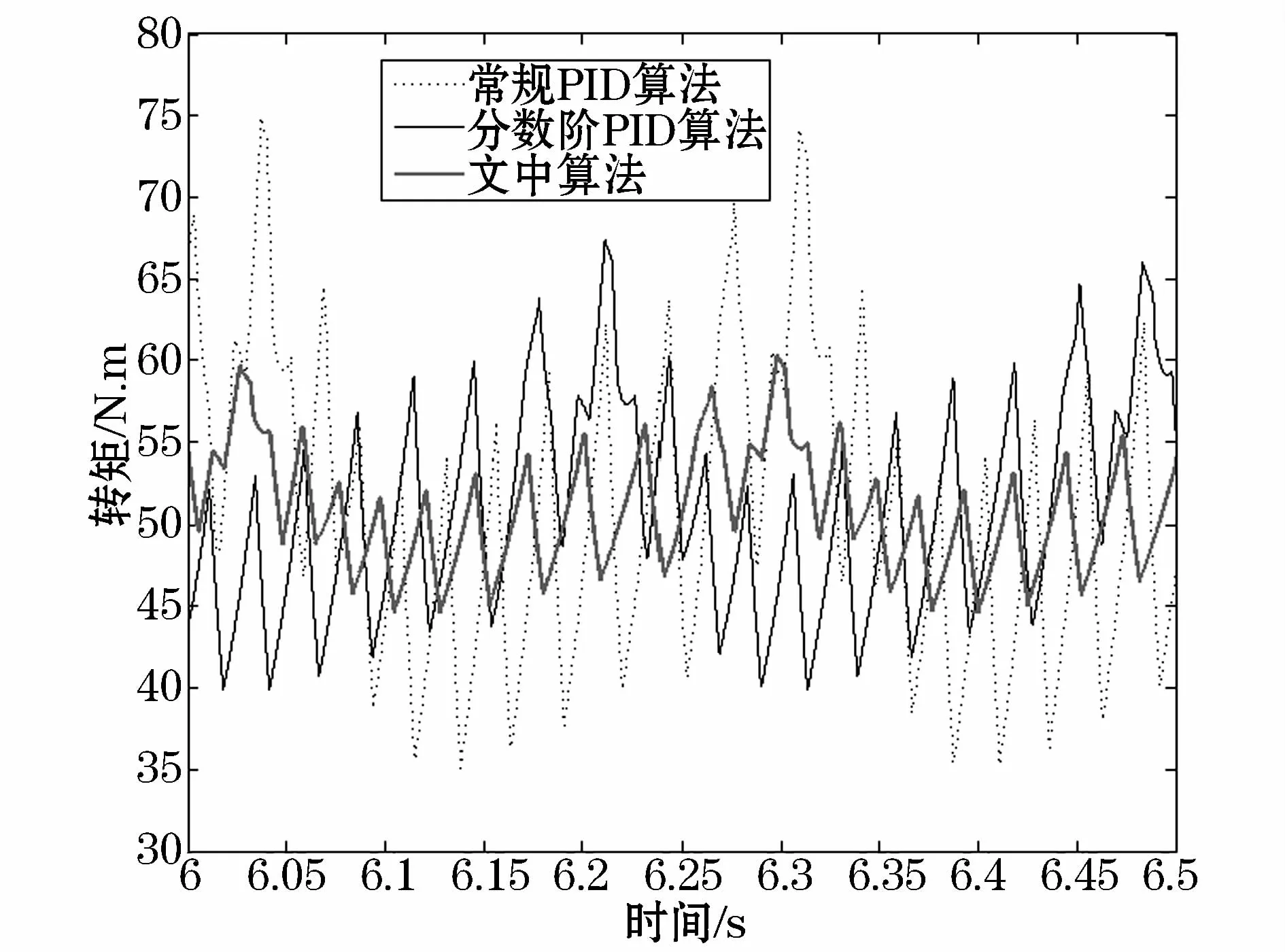
图6 三种控制算法输出转矩的对比Fig.6 Output torque comparison of the three algorithms

在转矩脉动方面，本文控制算法与常规PID控制算法、分数阶PID控制算法的对比结果如图6所示，从图中可以得出模糊分数阶PID控制算法的转矩脉动系数小，其方差数值为29.047 7，而常规PID的方差数值为38.874，分数阶 PID的方差数值为32.487 6。

4 结束语

本文利用模糊分数阶PID算法对开关磁阻电机的转速控制进行了分析与数字仿真。结果表明，与常规PID算法和分数阶PID算法相比，它极大地改善了开关磁阻电机的转速品质，具有鲁棒性好，调节时间快，超调量小、转矩脉动小的优点。由于分数阶控制算法的运算比较复杂，所以对算法的进一步优化，便于在微型控制系统中使用，将是下一步的研究工作。