基于价值函数的电动汽车充电价格引导研究
佟欣,郭春林,张明智
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
基于价值函数的电动汽车充电价格引导研究
佟欣,郭春林,张明智
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
电动汽车的大量接入将给电网的稳定运行带来危害,通过充电价格的调整可以合理引导电动汽车的充电行为,减小电动汽车负荷对电网的影响。基于价值函数推导出自弹性系数和互弹性系数的计算公式,在考虑对用户的引导程度不同和电网负荷波动的情况下提出了2种分时电价方案,并建立了电动汽车充电的分时电价引导模型。对比分析2种不同方案下的最优分时电价,结果表明实行分时电价可以对电动汽车用户的充电行为进行有效引导,并且峰谷电价差增大,更有利于平抑电网的负荷波动,提高用户充电的经济性。
电动汽车;电价引导;弹性系数;价值函数
0 引 言
近年来,由于化石能源的减少和汽车尾气污染的日益严重,电动汽车的发展已势不可挡。但电动汽车大规模接入电网充电,将对电力系统的运行与规划产生不可忽视的影响[1-3]。
我国也在大力推进电动汽车的发展。经测算,到2020年我国电动汽车保有量将超过500万辆。为了减轻电动汽车负荷给电网带来的压力,可以通过电价的杠杆作用,引导电动汽车负荷的合理分布[4]。国家发改委已正式下发《关于电动汽车用电价格政策有关问题的通知》,规定充换电设施经营商能够向受服务群众收取电费和一定的充换电服务费。自2020年1月1日起,充电服务收费按照国家规定实行市场调节价。电动汽车的充电价格影响着用户的充电选择,进而影响对电动汽车充电负荷的调控。
目前,国内外已有大量有关电动汽车充电负荷调控和引导的研究。电动汽车充电的调度可以在充分考虑电动汽车充电需求和配网负荷水平的基础上,通过配电网调度对电动汽车充电负荷进行直接的调控[5-8]。而近年来兴起的电动汽车充电的间接引导,也是有效调节负荷的方式。利用充电电价的变化对电动汽车充电行为进行引导,鼓励电动汽车车主调整充电时间[9-10]。文献[11]以减小电网峰谷差作为主要目标,结合电网分时电价时段划分与局域配电网负荷波动情况,提出了电动汽车充电分时电价时段划分方法。文献[12]在分析电动汽车放电成本和效益的基础上,给出了电动汽车放电电价定价的上下限,建立了电动汽车与电网互动的最优峰谷电价模型。文献[13]根据电网实时电价信息优化电动汽车用户充电电价触发值,降低用户充电成本,在此基础上建立了基于需求响应的电动汽车经济调度模型。文献[14-15]根据用户的价格偏好,提出电动汽车的智能充电控制算法。文献[16]兼顾电网的利益、电动汽车车主的利益和电动汽车车主的满意度,设计了一套能够影响电动汽车充电行为的最优峰谷分时电价定价方案。
本文基于价值函数,根据充电价格弹性系数的定义,推导出自弹性系数和互弹性系数的表达式,考虑对用户的引导程度不同与电网的负荷波动情况,建立电动汽车充电的分时电价引导模型,并采用遗传算法进行求解。对比算例中两种分时电价的最优结果,分析实行分时电价对电动汽车用户充电行为的引导作用。
1 基于价值函数的充电价格弹性系数计算
1.1 电动汽车充电价格弹性系数
电动汽车充电价格的波动,会影响用户调整充电计划,从而影响充电负荷的变化。在经济学理论中,价格往往是影响消费者购买行为的主要因素,本文忽略其他影响因素,研究充电价格的变化与充电负荷之间的关系。文中的电动汽车充电价格是指充电电价与充电服务费的总和,后文简称电价。用价格弹性系数ε表示电价的相对变动引起的电量需求量的相对变动[17]。
(1)式中:q为电动汽车的充电负荷;p为电动汽车充电电价;Δq和Δp分别表示充电负荷和电价的变化量。
实施分时充电电价时,用户的充电行为不仅受到本时段的充电价格影响,还与其他时段的充电价格有关[18],自弹性系数εii和互弹性系数εij的计算公式为:
(2)
(3)
式中:i,j代表不同时间段,为简便起见用1,2,3分别代表峰、平、谷时段(i,j=1,2,3);qi为i时段的电动汽车充电负荷;pi和pj分别代表电动汽车在i时段和j时段的充电电价。
1.2 基于价值函数的充电价格弹性系数计算
为了实现充电价格弹性系数的求解引入价值函数,该理论表明在每一种消费模式下,任何一对要素的输入量与输出量之间可以表示为比例固定的函数[19]。利用价值函数列出电力需求等式,描述电动汽车充电价格和充电负荷的关系,并且可以利用用户负荷数据和价格变化估计出未知参数,进而计算弹性系数。
Generalized Leontief价值函数定义了商品总费用的表达式,它与每一时段的商品价格和需求量有关[19]。本文主要研究电动汽车分时充电的总费用,它与充电电价、充电量有关,因此可以用价值函数的表达式进行计算,充电总费用可表示为
(4)
式中:F为电动汽车充电的总费用;h(qi)为电动汽车的电力需求量,它可以表示为不同时段电力需求量的函数;参数βij需要根据已知充电电价和需求量进行计算。根据价值函数的输入输出等式得到:
(5)
式中αij为未知参数,表示输入与输出之间的联系。充电费用与电价的变化率有关,为使用户的总花费最小,对电价求偏导:
(6)
每一时段的费用占总费用的份额wi的表达式:
(7)
式中:k=1,2,3。将式(6)代入式(7)得:
(8)
式中:μi为加入的扰动。未知参数αij和βij的求解,可以利用电价和负荷的多组数据,借助数据分析软件stata的似不相关回归函数,进行分析计算。
将式(6)—(8)代入式(2)和(3)中可得自弹性系数和互弹性系数的表达式:
(9)
(10)
2 电动汽车充电的分时电价引导模型
2.1 分时电价的充电负荷变化分析
实施分时电价时,电动汽车负荷对充电电价波动的响应,可以用负荷的变化量表示。根据已知的价格弹性系数,在实施分时电价后,计算出每一时段的负荷变化量。根据对用户的引导程度不同,分为以下2种不同的分时电价方案进行分析。
方案一:为了使部分用户充电习惯不受影响,增加用户的满意度,不改变原来的收费标准。在实施分时电价后,平时段的电价仍为原固定电价。
此时的峰时段的电价为
p1=(1+k1)p2
(11)
谷时段的电价为
p3=(1+k3)p2
(12)
式中:k1为峰时段的电价变化率;k3为谷时段的电价变化率;k2=0。
方案二:通过电价的引导尽可能使用户,避免在电网负荷的峰值进行充电,将负荷转移到谷时段。在实施分时电价后,各时段电价均做出调整。
假设各时段的电价变化率为ki,实施分时电价后的各时段负荷变化率为ri,则:
(13)
(14)
代入公式(2)和(3)得:
(15)
2.2 电动汽车充电的分时电价引导模型
电价引导的目的是减小电网的峰谷差,平抑电网的负荷波动。可以用负荷方差表示电网的负荷波动情况,同时考虑电动汽车用户的经济性和电网侧的收益等因素,建立电动汽车充电的分时电价引导模型。
选取电网的负荷方差最小作为目标函数,方差越小,代表负荷变化越平稳,按照1天24 h进行计算:
(16)
(17)
式中:S表示电网负荷的方差;PYn表示原电网在第n小时的负荷;qin为电动汽车在第n小时的负荷,i=1,2,3分别代表该负荷属于峰、平、谷时段;PS为电网加入电动汽车负荷后的日平均负荷。
一般来说,仅考虑电网侧的目标是不够的,还要考虑用户的利益问题。但本文是通过调整电价来控制负荷的变化,用户侧的充电费用最小与电网负荷波动最小的目标难以同时实现。因此,把用户的充电费用作为约束条件。具体约束条件包括以下几个方面。
(1)实施分时电价后,电动汽车用户总的电费用F1小于原来的充电费用F0:
F0=q0p0
(18)
(19)
(20)
式中:q0和p0分别代表未实施分时电价前的总负荷与电价。
(2)实施分时电价后,应使新的负荷曲线最大值小于原电网与电动汽车总负荷曲线最大值。
Pmax (21) 式中:Pmax为分时电价后的电网负荷曲线的最大值;P0max为原电网与电动汽车总负荷曲线最大值。 (3)对于供电公司侧,保证在实施分时电价后的收益大于原来的收益[20]: F0+F2>F1 (22) (23) 式中:F2表示供电公司因为减少设电网线路建设费和设备备用容量等获得的利益;J为电网的单位造价;σ为电网的经济周期年金系数。 (4)综合考虑用户侧和电网侧经济性的限制,电价应在一定范围内变化。 pi∈(pmin,pmax) (24) 2.3 电动汽车充电的分时电价引导模型的求解 电价引导模型最终需得到最优的分时电价,本质上是在一定范围内搜索满足条件的非线性最优化问题。遗传算法是一种基于自然选择和遗传变异等生物机制的全局性概率搜索算法,搜索过程不受优化函数连续性的约束,具有很高的并行性和较强的智能性,广泛应用于求解复杂的非线性最优化问题。 采用遗传算法求解最优分时电价的步骤如下: (1)将电网的负荷方差最小的目标函数作为适应值函数; (2)对分时电价进行编码构成初始种群; (3)计算初始电价的适应度; (4)对适应度较大的个体,进行选择、交叉和变异; (5)经过一代代的不断进化,最后收敛到一个最适应环境并满足约束条件的个体上,得到最优的分时电价。 3.1 研究对象及数据 本文以北京某区域的典型日负荷数据为电网基础负荷,具体数据如图1所示。利用蒙特卡洛算法模拟500辆电动汽车无序充电的负荷数据,充电功率按照 3 kW计算。将电动汽车的负荷加入到电网负荷得到系统总负荷曲线,如图2所示。未实施分时电价时,电动汽车的固定充电电价采用目前已实行的 1.2元/(kW·h)。分时电价的时段划分:峰时段为12:00—21:00;平时段为7:00—12:00和21:00—24:00;谷时段为0:00—7:00。 图1 原电网日负荷分布图Fig.1 Load distribution of original power system 图2 加入电动汽车负荷后的系统总负荷曲线Fig.2 Load of power system added electric vehicle charging load 为了求解弹性系数,利用电动汽车基础设施示范项目“The EV Project”的数据进行统计和分析[21]。采用数据分析软件stata,选取多组数据进行迭代,结合价值函数计算,最终得到弹性系数矩阵: 自弹性系数都为负数,表明当本时段的充电电价升高时,该时段的充电负荷下降。从互弹性系数来看,谷期电价是影响电动汽车用户充电行为的重要因素,当谷期电价降低时,用户会将峰时段和平时段的的负荷转移到谷时段。 3.2 不同方案的分时电价求解结果 分时电价方案一是以平时段的电价为基准,保持平时段的电价不变,利用电动汽车充电电价引导模型计算峰时电价和谷时电价。而方案二的各个时段电价均发生变化,计算此时的最优分时电价以及负荷变化情况。2种方案分别得到的各时段最优电价如表1所示。实施分时电价前后的电网总负荷变化情况如图3所示。 表1 不同方案的最优分时电价 元/(kW·h) 图3 实行最优分时电价后电网的负荷变化对比图Fig.3 Load variation of power system after executing optimal TOU price 由图3可知,在实行方案一时,因为峰时电价的升高和谷时电价的降低,引起了电动汽车负荷的变化,使原网的峰负荷下降,谷时负荷上升。但由于峰时段的电价升高,部分用户将充电时间转移到平时段,造成了在夜间21点时的用电量大量增加,形成新的负荷高峰,给电网负荷造成了冲击。在实行方案二的最优分时电价时,平时段的电价升高,谷时段的电价大幅降低,峰谷电价差增大,使峰时段和平时段的用户充电更多的转移到谷时段,并且没有产生新的负荷峰值,达到了削峰填谷的目的。 进一步分析比较实行分时电价前后用户的充电费用和负荷波动情况,如表2所示。 表2 3种情形下的用户花费与负荷波动情况 实行分时电价后,电动汽车用户充电的总费用均较固定电价的费用少,并且方案二中由于谷时段的电价降低,用户的费用相应有了大幅度的降低。负荷的方差反应了电网负荷的波动情况,实行分时电价后,电网的负荷波动减小,而且实行方案二的最优分时电价时方差最小。 结果表明,方案二的电价更为合理,为本文模型的最优分时电价。相比固定电价,实行电动汽车分时电价,能够对电动汽车用户的充电行为进行有效引导;并且对各时段的电价均作出调整,增大峰谷电价差,不仅可使用户的充电费用减少,还能够有效的平抑电网负荷的波动。 本文基于价值函数,根据充电价格弹性系数的定义,推导出自弹性系数和互弹性系数的表达式。根据对用户的引导程度不同,提出2种分时电价方案,考虑电网的负荷波动情况,建立电动汽车充电的分时电价引导模型,并采用遗传算法进行求解。以某区域电网为例,对比分析两种分时电价的最优结果,实行分时电价对电动汽车用户的充电行为有引导作用,使用户改变充电时间,进而降低电网的负荷峰值,并且调整各时段的电价,增大峰谷电价差,能更好地减小电网负荷波动,降低用户的充电费用。 [1]胡泽春,宋永华,徐智威,等.电动汽车接入电网影响与利用[J].中国电机工程学报,2012,32(4):1-10. HU Zechun,SONG Yonghua,XU Zhiwei, et al.Impacts and utilization of electric vehicles integration into power systems[J].Proceedings of the CSEE,2012,32(4):1-10. [2]高赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35(2):127-131. GAO Ciwei,ZHANG Liang.A survey of influence of electrics vehicle charging on power grid [J].Power System Technology,2011,35(2):127-131. [3]郭春林,于鹏,付金彦,等.规模化电动汽车有序充电对居民区配电网的影响[J].电力建设,2015,36(7):94-100. GUO Chunlin,YU Peng,FU Jinyan,et al.Influence of large-scale orderly charging of electric vehicle on residential distribution network [J].Electric Power Construction,2015,36(7):94-100. [4]曾正,赵荣祥,杨欢,等.电动汽车高渗透率的应对策略及换电站的最优规划[J].电力系统自动化设备,2012,32(9):7-13. ZENG Zheng,ZHAO Rongxiang,YANG Huan,et al.Responsive schemes to high penetration of electric vehicles and optimal planning of battery swap stations [J].Electric Power Automation Equipment,2012,32(9):7-13. [5]徐智威,胡泽春,宋永华,等.基于动态分时电价的电动汽车充电站有序充电策略[J].中国电机工程学报,2014,34(22):3638-3646. XU Zhiwei,HU Zechun,SONG Yonghua,et al.Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J].Proceedings of the CSEE,2014,34(22):3638-3646. [6]王锡凡,邵成成,王秀丽,等.电动汽车充电负荷与调度控制策略综述[J].中国电机工程学报,2013,33(1):1-10. WANG Xifan,SHAO Chengcheng,WANG Xiuli,et al.Survey of electric vehicle charging load and dispatch control strategies [J].Proceedings of the CSEE,2013,33(1):1-10. [7]YOU P,YANG Z,CHOW M Y,et al.Optimal cooperative charging strategy for a smart charging station of electric vehicles [J].IEEE Transactions on Power Systems,2016,31(4):2946-2956. [8]SUNDSTROM O,BINDING C.Flexible charging optimization for electric vehicles considering distribution grid constraints [J].IEEE Transactions Smart Grid,2012,3(1):26-37. [9]郑丹.电动汽车对电力系统的影响以及交互作用研究[D].广州:华南理工大学,2013. ZHENG Dan.Investigations on the impact and interactions between electric vehicles and power system [D].Guangzhou:South China University of Technology,2013. [10]葛少云,黄镠,刘洪,等.电动汽车有序充电的峰谷电价时段优化[J].电力系统保护与控制,2012,40(10):1-5. GE Shaoyun,HUANG Liu,LIU Hong,et al.Optimization of peak-valley TOU power price time-period in ordered charging mode of electric vehicle [J].Power System Protection and Control,2012,40(10):1-5. [11]孙晓明,王玮,苏粟,等.基于分时电价的电动汽车有序充电控制策略设计[J].电力系统自动化,2013,37(1):191-195. SUN Xiaoming,WANG Wei,SU Su,et al.Coordinated charging strategy for electric vehicles based on time-of-use price [J].Automation of Electric Power Systems,2013,37(1):191-195. [12]项顶,宋永华,胡泽春,等.电动汽车参与V2G的最优峰谷电价研究[J].中国电机工程学报,2013,33(31):15-25. XIANG Ding,SONG Yonghua,HU Zechun,et al.Research on optimal time of use price for electric vehicle participating V2G[J].Proceedings of the CSEE,2013,33(31):15-25. [13]潘樟惠,高赐威.基于需求响应的电动汽车经济调度[J].电力建设,2015,36(7):139-145. PAN Zhanghui,GAO Ciwei.Economic dispatch of electric vehicles based on demand response [J].Electric Power Construction,2015,36(7):139-145. [14]WANG B, HU B,QIU C,et al.EV charging algorithm implementation with user price preference[C]//Innovative Smart Grid Technologies Conference (ISGT), 2015 IEEE Power & Energy Society.Washington,DC:IEEE,2015,1-5. [15]BAHRAMI S,PARNIANI M.Game theoretic based charging strategy for plug-in hybrid electric vehicles[J].IEEE Transactions on Smart Gridvol,2014,5(5):2368-2375. [16]高亚静,王辰,吕孟扩,等.计及车主满意度的电动汽车最优峰谷分时电价模型[J].电力自动化设备,2014,34(2):8-13. GAO Yajing,WANG Chen,LYU Mengkuo,et al.Optimal time-of-use price model considering satisfaction degree of electric vehicle owners [J].Electric Power Automation Equipment,2014,34(2):8-13. [17]秦祯芳,岳顺民,余贻鑫,等.零售端电力市场中的电量电价弹性矩阵[J].电力系统自动化,2004,28(5):16-19. QIN Zhenfang,YUE Shunmin,YU Yixin,et al.Price elasticity matrix of demand in current retail power market[J].Automation of Electric Power Systems,2004,28(5):16-19. [18]邹文,吴福保,刘志宏.实时电价下插电式混合动力汽车智能集中充电策略[J].电力系统自动化,2011,35(14):62-67. ZOU Wen,WU Fubao,LIU Zhihong.Centralized charging strategies of plug-in hybrid electric vehicles under electricity markets based on spot pricing [J].Automation of Electric Power Systems,2011,35(14):62-67. [19]FENG G,SERLETIS A.Productivity trends in U.S.manufacturing: evidence from the NQ and AIM cost functions[J].Journal of Econometrics,2008,142(1):281-311. [20]谭忠富,王绵斌,张蓉,等.发电侧与供电侧峰谷分时电价联动的分级优化模型[J].电力系统自动化,2007,31(21):26-29. TAN Zhongfu,WANG Mianbin,ZHANG Rong,et al.Classification linkage optimization model of time of use power price between generating side and retail side [J].Automation of Electric Power Systems,2007,31(21):26-29. [21]STEPHEN G.EV project electric vehicle charging infrastructure summary report[R].U.S.Department of Energy,2011. (编辑 张媛媛) Price Guide of Electric Vehicles Charging Based on Cost Function TONG Xin, GUO Chunlin, ZHANG Mingzhi (State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China) The charging of large number of electric vehicles (EV) will affect the secure operation of power grid.In order to reduce the impact of charging load on the grid, the charging price can be adjusted to guide the charging behavior of EV owners.This paper derives the formulas of self-elastic coefficient and cross-elastic coefficient based on the cost function.And this paper establishes two time-of-use (TOU) price plans and a TOU price model for guiding EV charging with considering the motivation level of owners’ and the load fluctuation in power grid.Finally, this paper compares the optimal TOU prices between these two plans.The results show that TOU price can effectively guide the charging behavior of EV owners, and the increased difference between peak and valley load price will stabilize the load fluctuation in power grid and reduce the EV owners’ charging cost. electric vehicle; price guide; elastic coefficient; cost function 中央高校基本科研业务费专项资金资助项目(2015MS05);新能源电力系统国家重点实验室自主研究课题重点项目(LAPS2016-05) Project supported by Fundamental Research Funds for the Central Universities(2015MS05) TM 711 A 1000-7229(2016)09-0030-06 10.3969/j.issn.1000-7229.2016.09.004 2016-06-12 佟欣(1992),女,硕士研究生,主要研究方向为电动汽车充电设施及影响; 郭春林(1975),男,教授,主要研究方向为电动汽车充电设施及影响、次同步振荡分析与抑制等; 张明智(1993),男,硕士研究生,主要研究方向为电动汽车接入,储能系统及微网。3 算例分析
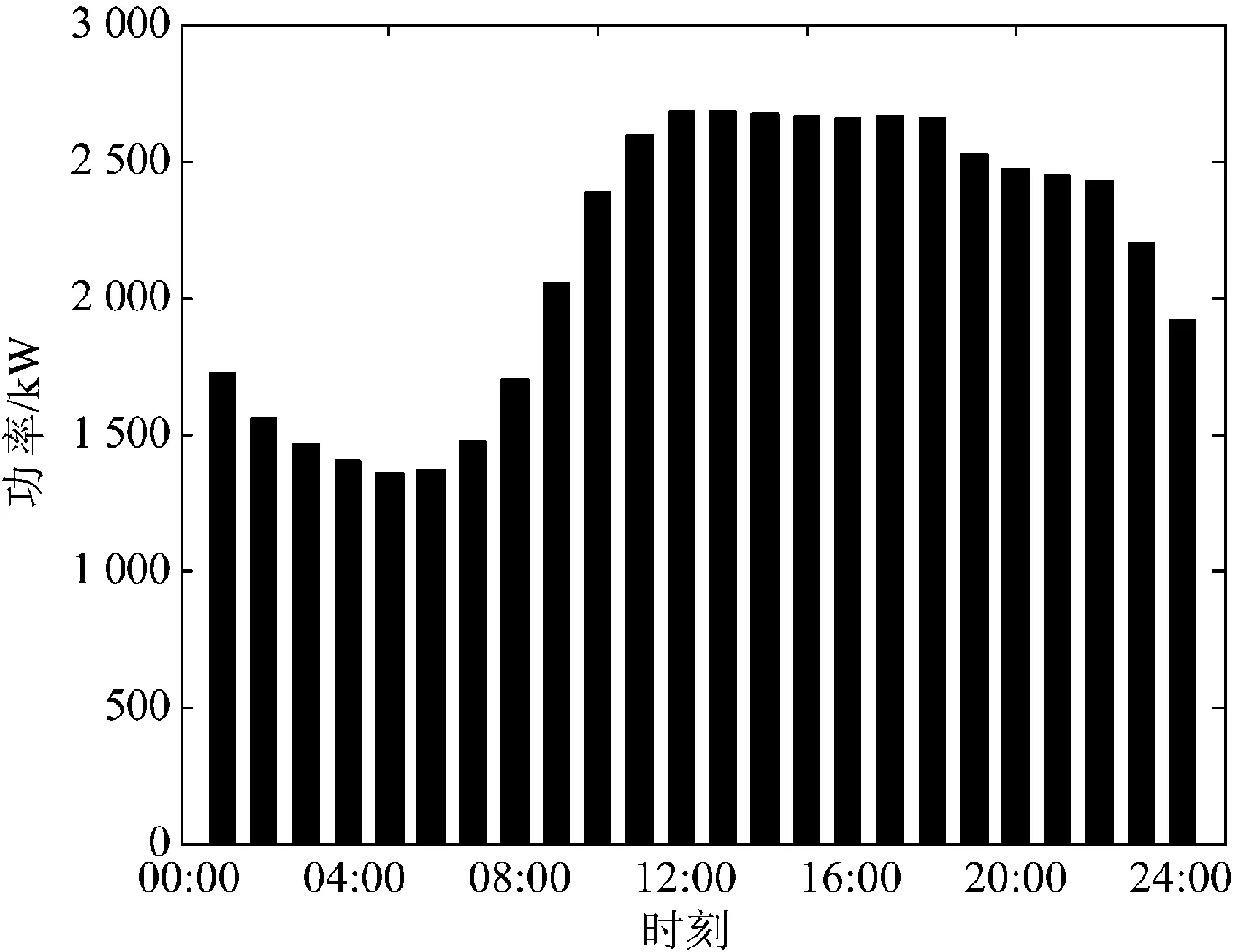


Table 1 Optimal TOU price under different plans

Table 2 User cost and load fluctuation under three cases
4 结 论

