液压启闭弧形闸门主框架内力计算研究
张 虎
(湖南省交通规划勘察设计院, 湖南 长沙 410008)
液压启闭弧形闸门主框架内力计算研究
张 虎
(湖南省交通规划勘察设计院, 湖南 长沙 410008)
弧形闸门是泄洪闸上应用较多的一种门型,主框架是其主要受力结构,因主框架属超静定结构,内力计算较为复杂,参数较多,目前尚无通用计算公式可供参考。对双主横梁下吊点液压启闭弧形工作闸门主框架的内力计算公式进行了推导,并给出了通用计算公式,公式经过湘江长沙综合枢纽和土谷塘航电枢纽中实际应用检验,证明是可行的,可为类似工程设计提供参考。
泄洪闸; 弧形闸门; 液压启闭; 计算公式
0 前言
弧形闸门因其启闭力小、操作方便、出水条件好(无明显空蚀及振动发生),而广泛应用于泄洪闸上。主框架是弧门的主要受力结构,主框架在支铰和侧止水的双重约束下,成为超静定结构,其构件内力分配与各构件之间的刚度比有关,计算过程较为复杂,参数较多。本文利用结构力学方法对双主横梁下吊点液压启闭弧形工作闸门主框架的内力计算公式进行了推导,并给出了一般计算公式,计算公式在湘江长沙综合枢纽泄水闸左汊和右汊弧形工作闸门设计中以及湘江土谷塘航电枢纽弧门设计中进行了应用,经过实践证明计算公式是可行的。
液压启闭弧形工作闸门一般公认为在闸门由最大水头挡水刚提升时受力是不利的,在此位置时闸门受到最大水头水压力的作用,同时受到闸门自重、侧止水摩阻力及启闭力的作用。
1 弧门主框架在静水压力作用下的内力计算公式的推导
采用结构力学位移法,对斜支臂主横梁式弧门在静水压力作用下的框架内力计算公式进行推导。
在进行计算公式推导之前,首先应明确以下几个基本条件:
1) 约束条件:支铰根据实际情况限制其线位移,允许角位移;门叶左右两边实际为侧止水,可限制门叶左右两边在垂直水流方向的线位移。
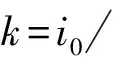
3) 根据结构力学位移法,杆端弯矩的一般公式为:
(1)
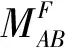
1.1 基本未知量
弧门框架的计算简图见图1,各参数如下:
q为主框架所承受的水压力;a为支臂中心线与主梁中心线交点至闸墙的距离;b为左右支臂中心线与主梁中心线交点的距离;d为支铰中心点至闸墙距离;h为支铰中心至主梁中心线距离。
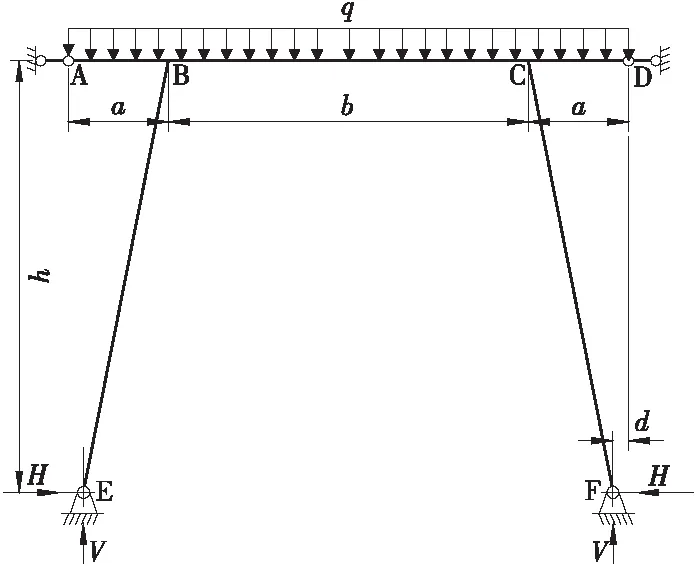
图1 水压力作用下弧门框架计算简图
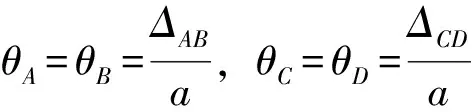
1.2 弧门各部位弯矩的计算公式
利用式(1)可得到弧门框架内各部位弯矩为式(2):
(2)
由结构力学可查得固端弯矩为:
(3)
联立方程:
MB=MBA+MBC+MBE=0
(4)
把式(2)和式(3)代入式(4)可得:
(5)
把式(5)代入式(2)便可得到弧门框架内各部位弯矩计算的一般公式最终为式(6):

(6)
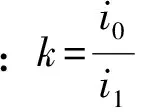
1.3 弧门支铰反力的计算公式
根据力的平衡原理,支铰的反力应为:
(7)
MBE+V(a-d)-Hh=0
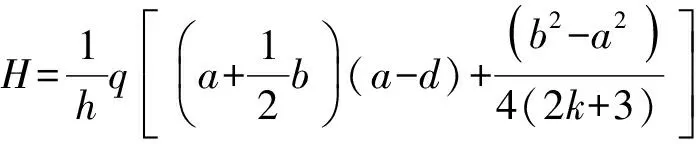
(8)
2 液压启闭机启门力和闸门自重及止水摩阻力共同作用下的弧门框架受力分析
2.1 支铰V向反力计算
闸门为对称结构,取结构的一半进行分析,计算简图见图2,图中受力T和G均为整体受力的一半,反力VS、VX为一侧支铰反力,其中各符号含义如下:
T为弧门启门力的一半;G为弧门自重和侧止水摩阻力合力的一半;N为T与G的合力;θS为上支臂与水平线的夹角;θX为下支臂与水平线的夹角;α为T与水平线的夹角;β为N与水平线的夹角(未知量);VS为T和G的合力在上框架的分力;VX为T和G的合力在下框架的分力。
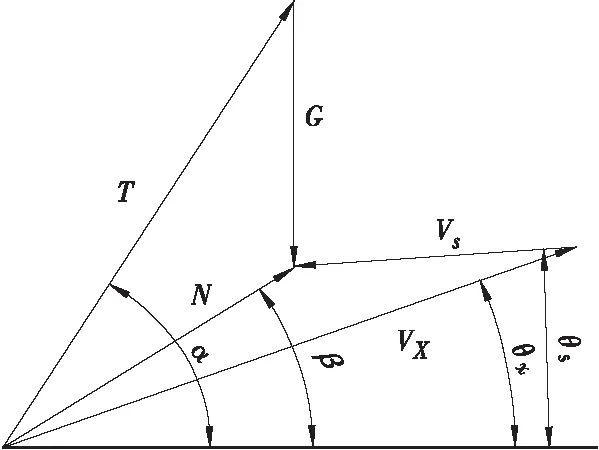
图2 启闭力及重力及框架受力关系图
参数T、G、α、θS、θX可根据闸门所处开度得知,通过已知参数经计算可得:
(9)
(10)
(11)
2.2 框架内力计算
由图2可知,上框架在本工况下的受力与静水压力作用下的效应是相反的,本工况会减弱静水压力作用下的上框架效应,下面重点分析下框架在本工况的内力,计算简图见图3。
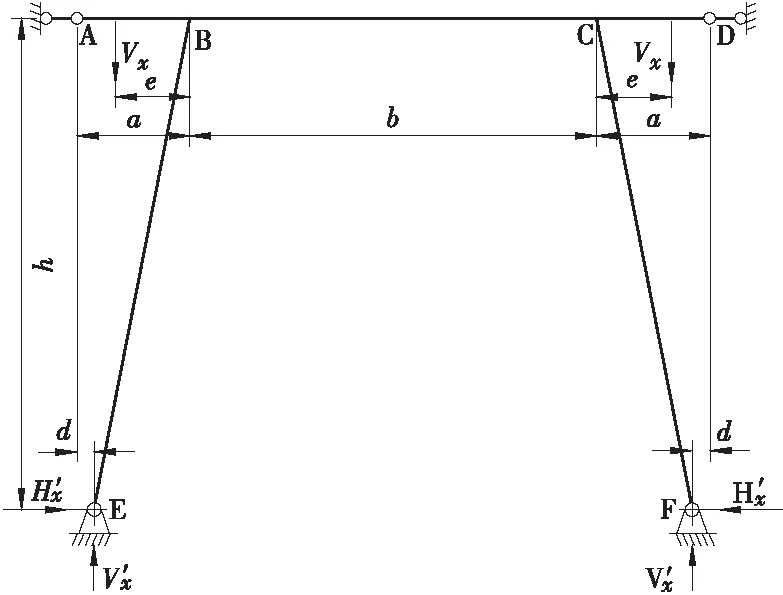
图3 启闭力在下框架内的计算简图
采用第1节的杆端弯矩公式,可得在启门力作用下的杆端弯矩为:
(12)
由MB=0,可得:
(13)
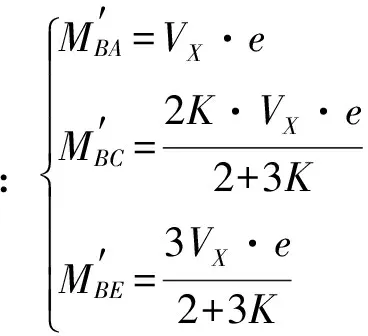
(14)
2.3 支铰反力计算
根据力的平衡:
(15)
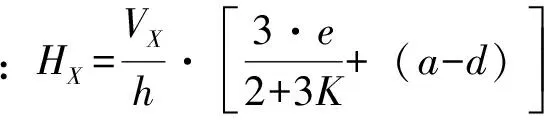
(16)
3 启门时弧门框架的合力合成
弧门由全关状态刚启门时,框架内力应为动水压力、启门力、闸门自重、侧止水摩阻力共同作用下的合成,根据《水利水电工程钢闸门设计规范》SL74-95,动力荷载可在静荷载的基础上乘以动力系数μ来考虑。由第1节和第2节分析可知,弧门上部框架的2种内力效应是相反的,内力合成时不能叠加,应在静水压力计算结果乘以动力系数μ;下部框架2种内力效应是相同的,内力合成应进行叠加,并乘以动力系数μ。
合成后的下框架内力为:
(17)
合成后的支铰反力为:
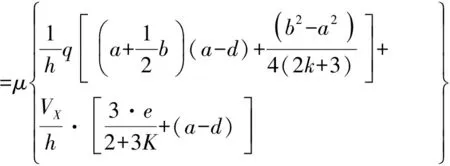
(18)
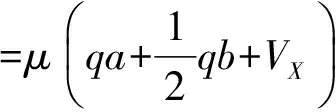
4 推导公式在工程实例中的应用
在湘江长沙综合枢纽和湘江土谷塘航电枢纽的设计过程中,运用以上推导公式对弧形闸门主框架和支铰内力进行了计算分析。湘江长沙综合枢纽2012年9月正式蓄水,湘江土谷塘航电枢纽2014年12月正式蓄水,两枢纽自蓄水以来弧门运行状态良好,经受住了实践检验。
在弧门设计过程中可根据《水利水电工程钢闸门设计规范》及各厂家提供的液压启闭机设计参数首先对弧门和启闭机进行布置,并根据布置通过试算的方法首先确定弧门的各结构件尺寸,并得到弧门自重和启闭力,此过程略,这里重点介绍利用以上推导公式对长沙枢纽及土谷塘枢纽弧门进行复核计算。
4.1 弧门工程特性
长沙枢纽及土谷塘枢纽弧门立面图见图4,弧门特性表见表1。
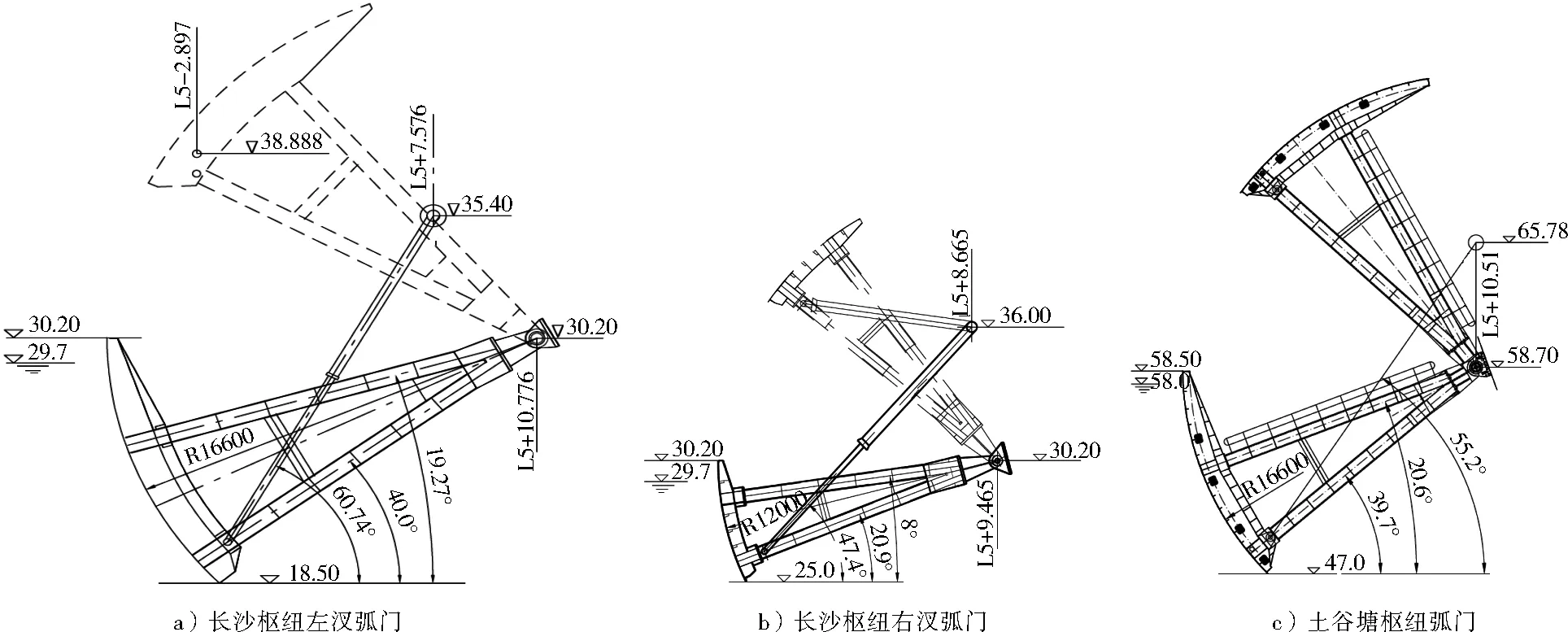
图4 弧门立面图
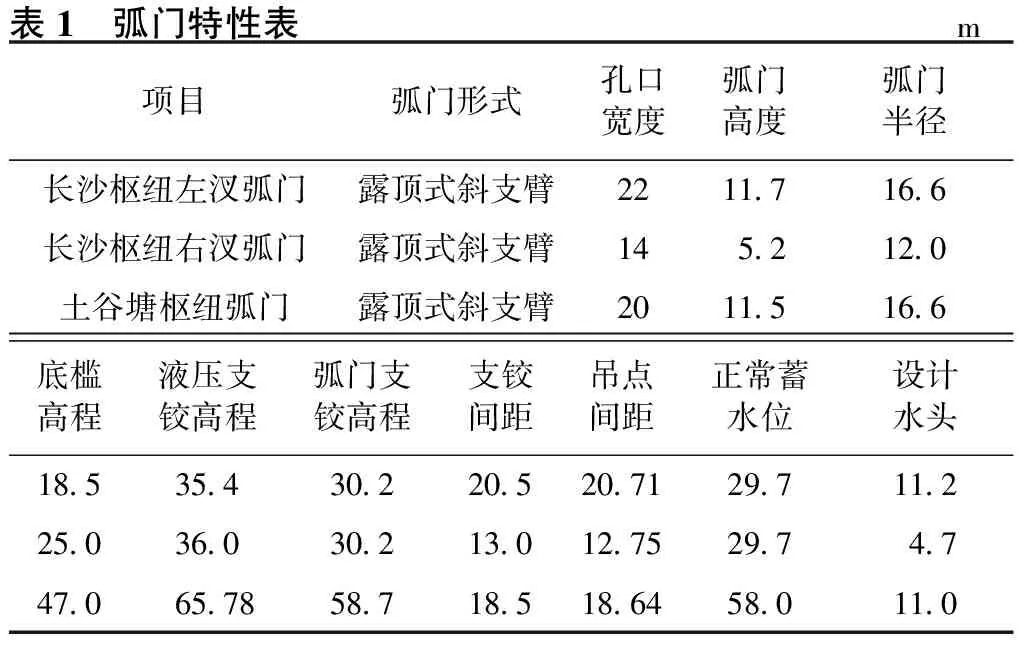
表1 弧门特性表m项目弧门形式孔口宽度弧门高度弧门半径长沙枢纽左汊弧门露顶式斜支臂22117166长沙枢纽右汊弧门露顶式斜支臂1452120土谷塘枢纽弧门露顶式斜支臂20115166底槛高程液压支铰高程弧门支铰高程支铰间距吊点间距正常蓄水位设计水头185354302205207129711225036030213012752974747065785871851864580110
4.2 计算参数
弧门计算参数表见表2。
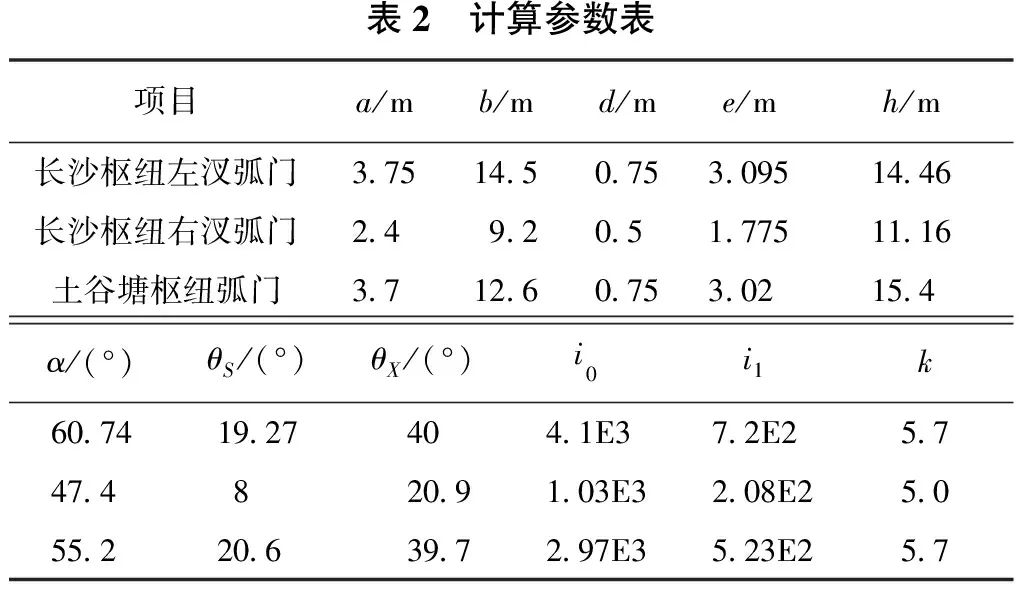
表2 计算参数表项目a/mb/md/me/mh/m长沙枢纽左汊弧门37514507530951446长沙枢纽右汊弧门24920517751116土谷塘枢纽弧门37126075302154α/(°)θS/(°)θX/(°)i0i1k607419274041E372E2574748209103E3208E250552206397297E3523E257
4.3 基本外力参数表
经初步计算得到弧门所受基本外力参数见表3。
4.4 计算结果
把以上参数代入式(11)、式(17)、式(18)得到下主框架内力计算结果见表4。
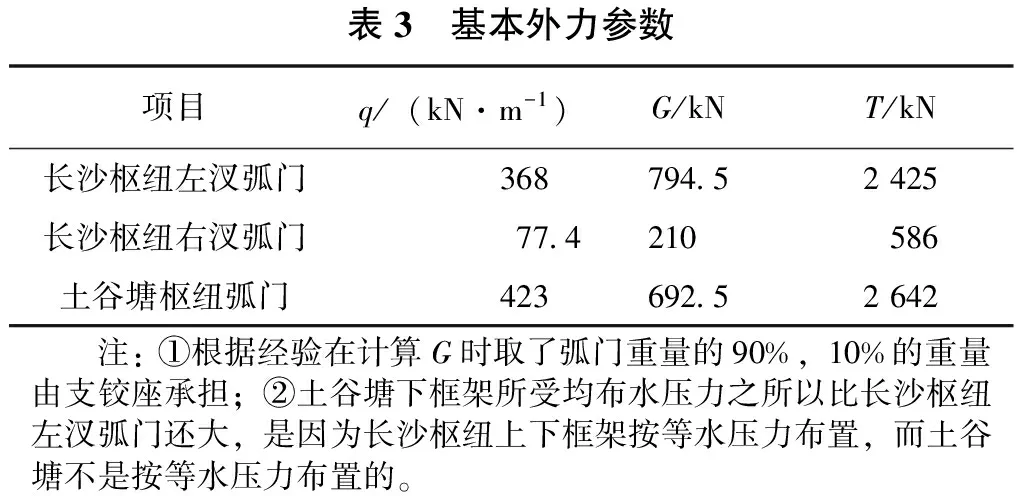
表3 基本外力参数项目q/(kN·m-1)G/kNT/kN长沙枢纽左汊弧门36879452425长沙枢纽右汊弧门774210586土谷塘枢纽弧门42369252642 注:①根据经验在计算G时取了弧门重量的90%,10%的重量由支铰座承担;②土谷塘下框架所受均布水压力之所以比长沙枢纽左汊弧门还大,是因为长沙枢纽上下框架按等水压力布置,而土谷塘不是按等水压力布置的。
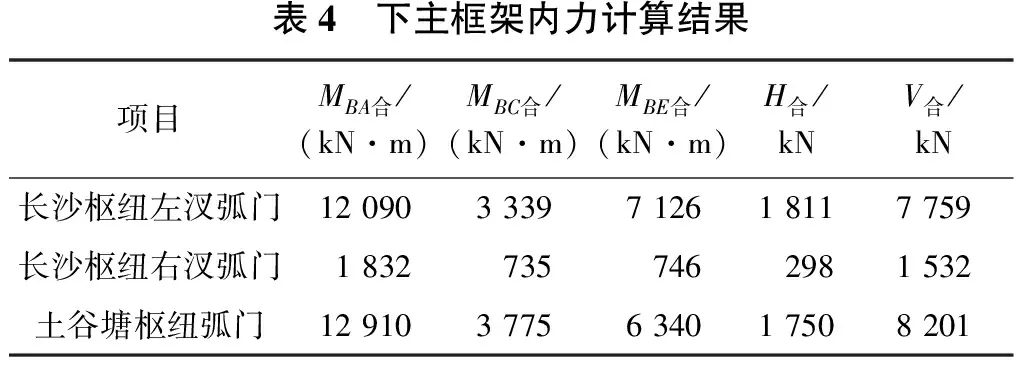
表4 下主框架内力计算结果项目MBA合/(kN·m)MBC合/(kN·m)MBE合/(kN·m)H合/kNV合/kN长沙枢纽左汊弧门120903339712618117759长沙枢纽右汊弧门18327357462981532土谷塘枢纽弧门129103775634017508201
5 结语
本文在一定假设条件的基础上利用结构力学位移法对弧形闸门在正常挡水时主框架的内力和闸门启门瞬间在启门力、自重、侧止水摩阻力作用下的主框架内力分别进行了推导,并最后给出了弧形闸门启门瞬间主框架的内力合力计算公式,公式经在长沙综合枢纽和土谷塘航电枢纽工程中应用检验,证明是可行的,可为类似工程设计提供参考。
[1] 杨逢尧.水工金属结构[M].北京:中国水利水电出版社,2005.
[2] 安徽省水利局勘测设计院.水工钢闸门设计[M].北京:水利水电出版社,1980.
[3] 龙驭球,包世华.结构力学[M].北京:高等教育出版社,2000.
[4] 水电站机电设计手册编写组.水电站机电设计手册 金属结构(一)[M].北京:水利水电出版社,1988.
1008-844X(2016)04-0169-05
U 641
A

