斜交空心板桥的动力特性分析

吴 桥

(中交二公局第三工程有限公司， 陕西 西安 710016)

斜交空心板桥的动力特性分析

吴 桥

(中交二公局第三工程有限公司， 陕西 西安 710016)

以106国道上某桥为背景，建立简支斜交空心板桥空间有限元模型，计算不同斜交角度下的频率值，根据计算数值结果，采用最小二乘法进行基频规范公式修正，得到角度修正后斜交空心板桥的基频计算公式，修正公式准确计算出斜交空心板桥的基频值。同时分析预应力钢筋效应对斜交空心板桥的频率影响。

斜交空心板； 频率； 公式修正； 预应力钢筋效应

0 引言

为满足线型的要求，中国高速公路网和城市立交桥的修建中涌现出大量的斜交桥。迄今为止，对于斜交桥的静力性能，国内外学者进行了大量的研究[1-5]。相对来说，动力特性分析却深入较少，夏樟华等以深圳元朗桥为背景，通过对实桥的频率、振型、阻尼比现场测试和识别，建立了三跨连续T梁桥的有限元模型，进行对比分析，总结了斜交T梁的动力特性[6]，认为三向约束的实体模型能较好的模拟桥梁的真实状态，有限元模型计算出来的频率值与实测值吻合较好；何旭辉等对PC斜交箱梁的振动特性模型试验的研究，得到了PC斜交箱梁桥的振型与斜交角度之间的关系[7]，认为斜交箱梁的振型明显有扭转成分，在较低阶(第3阶)就开始明显出现扭转，而正交单排支座体系箱梁桥要到第7阶。夏桂云等用梁单元建立了斜交空心板桥的计算模型，并对支座对称与不对称情况进行了计算，得出了一些关于斜交空心板桥动力特性的结论[8]，认为用梁单元建立的位移模式求解方程适用于两点支承也适用于多点支承，计算得到空心板桥的基频随斜交角度的增大而增大，这些都较好地指导各自桥型的建设。

在中小跨径的桥型中，预应力混凝土空心板桥以其自重轻、抗震抗裂性能好、稳定性高的特点而被广泛采用，在此种桥型的设计和检测中，动力特性的基频计算通常采用现行《公路桥涵设计通用规范》(JTG D60-2004)(简称《桥规》)中规定的计算方法，其规定为：

这一计算规定给我们带来了一些值得思考的问题:

1) 《桥规》中规定的计算方法只适用于正桥，对于弯扭耦合的斜桥，尤其是当斜交角度较大时，实测得出的频率值往往又与正桥不同。

2) 没有考虑预应力钢筋对桥梁动力特性的影响，虽然夏樟华等曾做过考虑预应力钢筋对桥梁动力特性影响的研究[9]，但也只针对于正桥单片梁。

3) 斜交桥梁计算冲击系数用到的基频计算公式并没有单独考虑，而是仍然采用正交角的计算公式，这与实测明显不符。

针对以上问题，本文以106国道上某桥——简支斜交空心板桥为背景，应用大型通用有限元软件ANSYS建立考虑预应力钢筋效应的空间有限元模型，计算不同斜交角度下的前三阶频率，得出了频率随斜交角度的变化规律，并根据计算结果对斜交空心板桥的基频规范公式进行角度修正，角度修正后的基频公式能较准确地计算出斜交板桥的基频值，同时本文还探讨了预应力钢筋效应对斜交空心板桥动力特性的影响。

1 工程背景及计算模型

1.1 工程背景

106国道上某桥是一座新修的预应力混凝土简支斜交空心板桥，桥面连续，斜交角度30°，设计荷载为公路I级。

1.2 有限元模型

在空间有限元模型的建立中，空心板混凝土采用SOLID65单元，钢筋采用LINK8单元，全桥共有61 200个SOLID65，考虑预应力时1 440个LINK8单元。钢筋与混凝土的共同作用通过约束方程方法实现，约束方程的方法是钢筋的节点与其相邻的数个混凝土节点建立约束方程而共同作用。采用初应变的方法来模拟预应力的大小。如图1，图2。

图1 混凝土单元离散图

图2 混凝土单元与钢筋单元建立约束后效果图

2 斜交空心板动力特性数值分析

2.1 频率随斜交角度变化规律

分别计算斜交角度等于0°、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°这11种斜角度的模态，得到前三阶竖向振动频率f1、f2、f3进行对比分析，结果见图3。

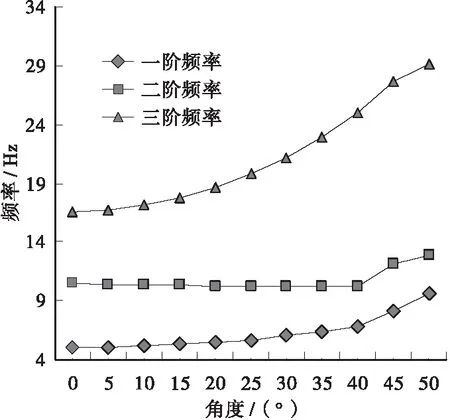
图3 不同斜交角度下的频率值

从图3可以看出在角度小于等于40° 时一阶频率随斜交角度的增加而增大，角度频率曲线平缓，二阶频率随斜交角度的增加基本不变，竖向频率值均在斜交角度为40° 时明显增大。本文计算结果与夏樟华所计算的T梁相比[6，9](见图4)，竖向频率变化趋势基本一致，但本文计算的一、三阶竖向频率随斜交角度的变化更明显，这也反映了频率随斜交角度的变化规律还与截面形式有关。

图4 夏樟华所计算的13 mT梁在不同斜交角度下的频率值

2.2 基频的修正

将基频计算的结果用最小二乘法进行拟合，得到角度修正后规范基频的计算公式，并进行角度修正公式的误差分析和试验检验，将误差分析结果列于表1，修正公式如下。

将修正公式绘制成函数图像，为了更形象地反映角度修正公式的图像，函数图像如图5。

由表1可知，角度修正后的公式与ANSYS计算的结果误差甚微，曲线拟合的较好。同时将岳阳

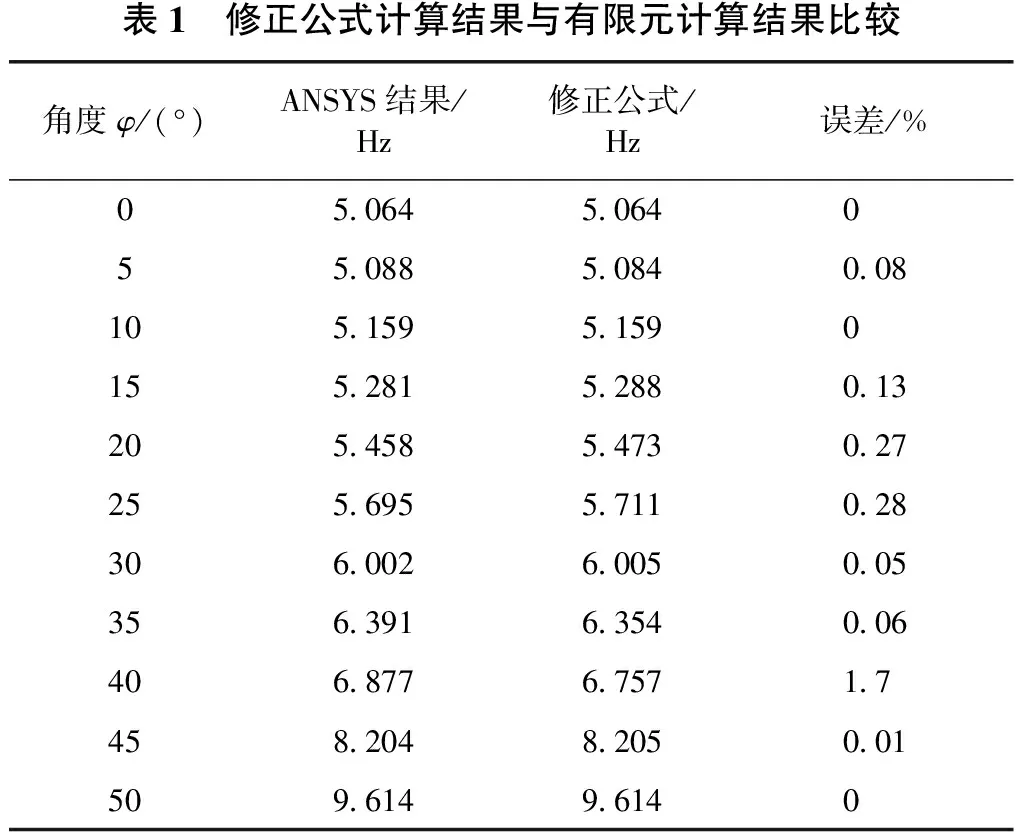
表1 修正公式计算结果与有限元计算结果比较角度φ/(°)ANSYS结果/Hz修正公式/Hz误差/%0506450640 5508850840081051595159015528152880132054585473027255695571102830600260050053563916354006406877675717458204820500150961496140

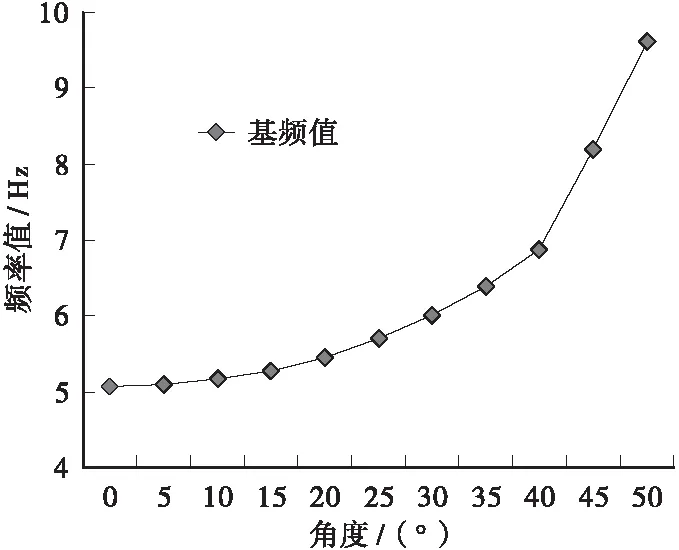
图5 角度修正公式函数图像

境内106国道上的某桥用修正公式计算的结果与现场测试的基频结果做比较以进行检验，该桥测试跨的跨径为20 m，斜交角度30°，现场测得的基频值为5.8 Hz，而采用修正公式计算的频率为6.005 Hz，比较后可以得出，修正后规范公式计算出的斜交空心板桥的基频值较准确，可以作为斜交空心板桥的基频计算公式。

3 考虑预应力钢筋的影响

106国道上某桥预应力布置为2束，单块板布

置图如图6，其中N1束为5Φs15.2，N2束为4Φs15.2，张拉力控制力为σk=0.75fpk。

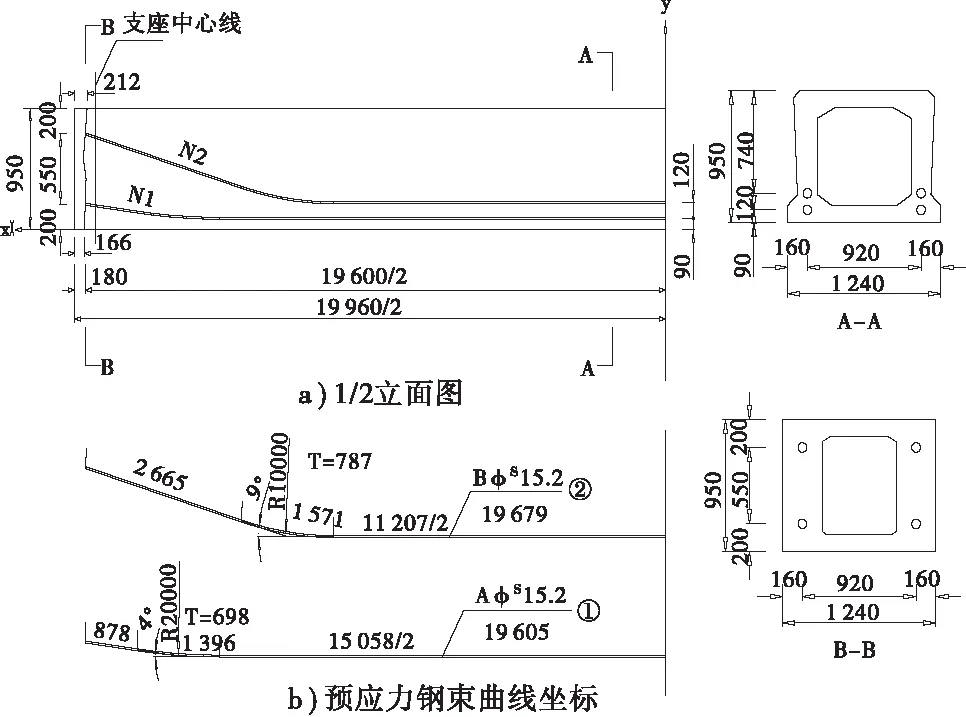
图6 预应力钢筋布置图(单位：mm)

在建立有限元模型时钢筋与混凝土通过约束方程的方法联系起来共同作用，约束方程方法比节点耦合和实体力筋的方法更方便，混凝土单元划分的质量也更好。

全桥9块板的钢筋单元离散图如图7所示。

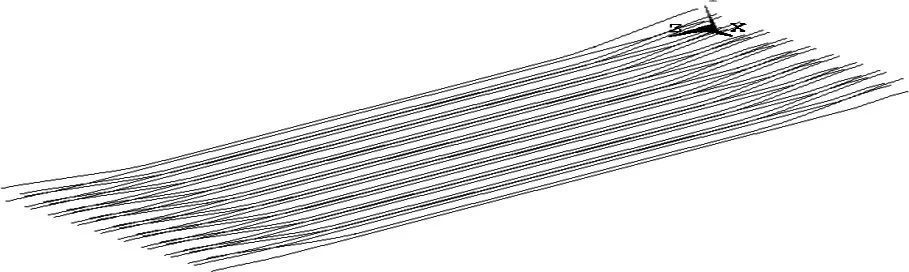
图7 预应力钢筋有限元模型

计算了张拉控制力在0.25fpk、0.5fpk、0.75fpk情况下，斜交角度分别为0°、10°、20°、30° 4种工况下的竖向频率值，与未考虑预应力效应的情况对比分析，将结果列于表2。

由表2可知，考虑预应力钢筋与不考虑预应力钢筋的情况对比，空心板桥的一阶竖向频率随预应力的增大而增大，对于这一结论，本文计算结果支持Saiidi等[10]人的观点；二阶竖向频率在斜交角

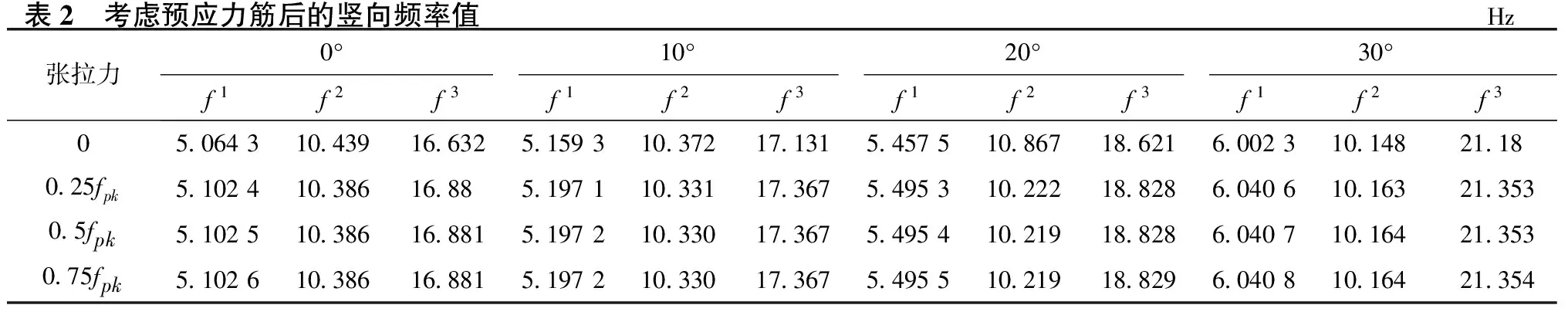
表2 考虑预应力筋后的竖向频率值Hz张拉力0°10°20°30°f1f2f3f1f2f3f1f2f3f1f2f3050643104391663251593103721713154575108671862160023101482118025fpk5102410386168851971103311736754953102221882860406101632135305fpk510251038616881519721033017367549541021918828604071016421353075fpk510261038616881519721033017367549551021918829604081016421354

度0°、10°、20°的时候随预应力的增大而减小，斜交角度30°的时候随预应力的增大而增大；三阶竖向频率随预应力的增大而增大，这点也说明了规范公式未考虑预应力钢筋参数对桥梁频率影响的合理性。

4 结论

1) 角度小于等于40°时一阶频率随斜交角度的增加而增大，角度频率曲线平缓，二阶频率随斜交角度的增加基本不变，前三阶竖向频率值均在斜交角度为40°时明显增大，通过对比分析，发现频率随斜交角度的变化规律还与截面形式有关。

2) 对规范的基频计算公式进行角度修正，修正后的公式与ANSYS计算的结果误差甚微，同时用现场测试的结果进行检验，检验结果也说明了修正后的规范公式计算出的斜交空心板桥的频率值较准确，可以作为斜交空心板基频的计算公式。但该公式是否适合其它截面形式的斜交桥还有待讨论。

3) 考虑预应力钢筋的情况比不考虑预应力钢筋的情况一阶竖向频率要大，对于这一结论，本文计算结果支持Saiidi等[10]人的观点，二阶竖向频率在斜交角度0°、10°、20°的时候随预应力的增大而减小，斜交角度30°的时候随预应力的增大而增大；三阶竖向频率随预应力的增大而增大。但无论是增大还是减小，都不明显。

[1] 刘小燕，韦成龙，欧阳祥森，等.装配式斜交空心板桥受力特性分析[J].公路工程，2007，32(4)：45-48.

[2] 魏炜，李满囤，钢筋混凝土斜板桥极限承载力试验[J].西安公路交通大学学报，2001，21(4)：46-49.

[3] 李国豪.斜交结构的斜梁桥的荷载横向分布分析[J].同济大学学报，1994，22(4)：395-400.

[4] 程翔云.对简支梁桥荷载横向分布系数计算模型的改善[J].公路工程，2007，32(4)：124-127.

[5] 陈星，李立峰.斜交板桥开裂原因分析及荷载试验[J].湖南交通科技，2004，30(1)：73-75.

[6] 夏樟华，宗周红.三跨斜交T梁动力特性分析[J]. 振动与冲击，2007，26(4)：147-150.

[7] 何旭辉，盛兴旺，陈政清.高速铁路PC斜交箱梁桥振动特性模型试验研究[J].铁道学报，2002，24(5)：89-92.

[8] 夏桂云，俞茂宏，李传习，等.斜桥动力特性[J]. 交通运输工程学报，2009，9(4)：15-21.

[9] 夏樟华，宗周红.预应力对混凝土梁动力特性的影响分析[J].振动与冲击，2007，26(7)：130-134.

[10] Saiidi M，Douglas B，feng S.Prestress force effect on vibration frequency of concrete bridges[J].Journal of Structural Engineering,1994，120(7)：2233-2241.

1008-844X(2016)04-0082-04

U 448.21+2

A