大跨度悬索桥有限元建模及动力特性分析
杨 亚
(重庆交通大学 土木工程学院, 重庆 400074)
大跨度悬索桥有限元建模及动力特性分析
杨 亚
(重庆交通大学 土木工程学院, 重庆 400074)
采用ansys软件对大跨度悬索桥进行有限元模型的建立,讨论动力特性的影响因素。对模型进行动力分析,获得桥梁的频率和振型。讨论恒载与预应力对动力特性影响,总结悬索桥动力特性并进行桥梁的抗风性能计算。
悬索桥; 有限元; ansys; 动力特性; 抗风
1 工程概况
泸州市长江二桥(城东)及连接线工程位于泸州市城东片区,连接沙茜CBD与高坝组团。道路规划定位为城市主干路,设计时速60 km/h,标准路幅宽度为40 m,两侧各40 m宽控制绿带,双向8车道。二桥缆索跨度布置为214 m+576 m+215 m,所有缆索系统均采用镀锌钢丝材料,其中主缆采用9 652根Φ5.2 mm镀锌高强度无松弛平行钢丝,吊索、斜拉索采用85根Φ7.0 mm镀锌高强度无松弛平行钢丝HDPE护套成品。加劲梁全长576 m,采用钢桁梁方案,梁高8.735 m,采用Q345号钢;桥面宽度30.1 m;斜腹杆、边纵梁均采用工字型或H型截面,上下弦杆采用闭合箱型截面,横梁为每隔3.6 m的倒T型截面;桥面纵向加劲肋采用抗弯刚度较大的“U”形加劲肋。缆索全部采用地锚式。全桥整体布置如图1所示,典型横断面如图2所示。

图1 悬索桥整体布置(单位: cm)

图2 标准段钢桁梁断面示意
2 空间有限元建模
悬索桥有限元模型的主梁主要有两种不同建模方式,一是确定桁架各个构件具体位置建出全桁架模型;二是先计算加劲桁架的抗弯刚度和扭转刚度,然后用一根具有等效刚度的主梁来代替加劲桁架,称为单主梁模型。第2种方法较为方便且计算量小,但是需要计算桁架的扭转质量矩,应用不好会使结果与实际有差异。由于截面质心与扭转中心不重合,通过振型图可知存在弯扭耦合现象,然而这种结果很难体现在单主梁的模型中。本文采用前一种方式建模,有限元模型如图3所示。建立模型时悬索桥具体构造如下:
1) 斜腹杆、上下弦杆、边纵梁、横梁均采用各自截面属性,材料为Q345钢材。桥塔简化为多个截面属性的“塔”状造型。加劲桁架与桥塔均采用ansys中Beam4单元。Beam4单元是一种具有压、拉、扭、弯特性的单元,两端节点具有X、Y、Z方向的共6个自由度。
2) 吊杆和主缆采用Link10杆单元,具有相同的截面和材料属性。Link10单元是一种具有双线性劲度功能的杆系构件,能够模拟仅受拉或受压的结构,还能够通过实常数被赋予初应力。
3) 带“U”形加劲肋的桥面板用一根等效截面的梁单元来假设,此梁单元通过横梁与主桁连接,很好地模拟了悬索桥的板桁结合构造。
4) 作动力分析时,需要形成质量矩阵,当对结构进行简化时,某些次要的构件就不需要建在模型里面,而把其质量留下即可。桥面铺装的质量通过Mass21质量单元来模拟,计算出恒载总的质量然后均铺于桥面节点。

图3 悬索桥有限元模型
3 动力特性的影响因素
3.1 恒载的影响
悬索桥的重力刚度是指其在恒载作用下缆索系统存在较大的拉力而具有抵抗一定变形的能力。缆索系统的初应力是重力刚度的来源,初应力直接由恒载产生。随着桥梁跨径的增加,加劲桁梁的抗弯刚度逐渐低于缆索系统轴向刚度。所以在结构动力分析时,重力刚度的影响有必要考虑进去。有限元分析中一般先进行静力计算,此时重力刚度的存在使得全桥的刚度矩阵进行了更新,再进行模态分析比较准确。
3.2 缆索初应力的影响
悬索桥在施工过程中缆索和桥面的位置在不断发生着变化,通过调整缆索的轴力使得成桥线性达到预先设定的目标,因此有限元模型只能通过成桥线型来确立。在有限元模型中,缆索初应力由改变Link10单元的实常数初应变来控制,通过对模型修改,当符合以下要求时主缆初应变认为最优。
1) 成桥时桥身变形最小;
2) 成桥时加劲桁梁内力最小;
3) 缆索张拉力与理论值一致。
最后,进行模型的经济学验证,常数a0等于11 025.12,即在碳交易金额和地区生产总值均为0的情况下,二氧化碳的自发排放数量为11 025.12万吨,符合假设;系数a1等于-2.72×10-5,即碳交易金额与碳排放数量成反比,以1990年为基期核算的碳交易金额对碳排放数量的影响系数为-2.72×10-5,符合假设;系数a2等于0.009 7,即地区生产总值与碳排放数量成正比,以1990年为基期核算的地区生产总值对碳排放数量的影响系数为0.009 7,符合假设。
在此条件下建立的有限元模型的受力更接近于真实情况。
4 模态分析
模态分析用于评价结构的动力特性,反映了结构的质量分布和刚度指标,模态分析结果为反应谱分析、动力时程分析提供基本的动力特性数据,因此对桥梁结构的抗震设计和抗风稳定性研究具有重要意义。本模型采用分块兰索斯法求解模态。采用特征向量进行兰索斯迭代的计算,内部使用稀疏矩阵直接求解器求解。
在李廉锟所著《结构力学》[1]一书中,对简支梁在指定挠度下的振型进行分解后发现,前阶振型所占比重比后阶振型小得多,多自由度结构的动力位移主要是由前几个较低频率的振型组成,更高的频率则影响很小,可略去不计。因此本文取前7阶振型。
此外,对于拟建的泸州长江二桥的动力特性结果,有必要在成桥后通过动载试验验证其可靠性并对模型进行修正。
为研究吊杆和主缆的预应力以及恒载对悬索桥模态分析的影响,选取了3种荷载工况来计算。
工况1:不考虑自重影响,也不设置主缆与吊杆预应力;
工况2:考虑自重,不设置主缆与吊杆预应力;
工况3:同时考虑自重并且设置主缆与吊杆的预应力。
表1给出了3种荷载工况作用下悬索桥前7阶频率。对比工况1和工况2可知恒载对悬索桥频率影响比较大,对侧弯频率的影响要小于竖弯和扭转,恒载存在与否频率相差均在30%以上。对比表2刘忠平[2]对自锚式三汊矶湘江大桥有无恒载动力特性分析,三汊矶湘江大桥在恒载作用下前7阶频率相差最大为8%。笔者认为自锚式悬索桥在恒载作用下会在主梁内产生巨大的轴向压力,而地锚式悬索桥仅仅在主缆和吊杆处产生力的作用,这点不同导致了恒载对地锚式悬索桥频率的影响比自锚式悬索桥频率的影响要明显很多。

表1 模态分析结果阶数频率/Hz工况1工况2工况3振型描述1019530120901220主梁侧弯2031070207702116主梁反对称竖弯3044440258402596主梁正对称竖弯4059570320103233主梁扭转5063690387503914主梁二阶正对称竖弯6078280395404013主梁反对称侧弯+缆索扭转710088044220447主梁二阶反对称竖弯
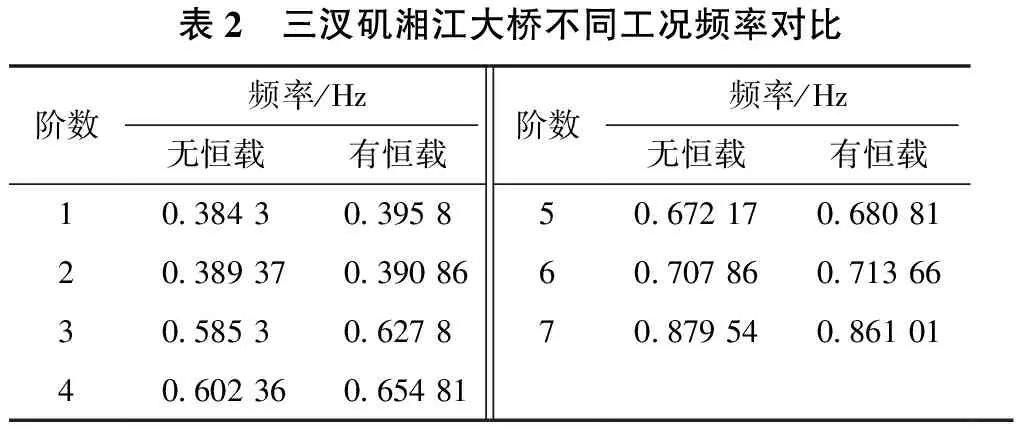
表2 三汊矶湘江大桥不同工况频率对比阶数频率/Hz无恒载有恒载阶数频率/Hz无恒载有恒载103843039585067217068081203893703908660707860713663058530627870879540861014060236065481
对比工况2和工况3可知主缆、吊杆的预应力对频率的影响比较小。为了充分验证预应力对频率的影响,采用了多个初应变进行分析。采用不同初应变使跨中挠度有一定差别,调试中得到的跨中挠度分别为0.049、0.21、1.35 m,对比发现频率差异均在1%以内(如表3所示)。

表3 不同跨中挠度频率对比阶数不同跨中挠度时频率/Hz0049m021m135m1012200122101223202116021200212830259602597025994032330323203229503914039180392760401304020040327444724447844483
前几阶振型图见图4所示。

主梁侧弯
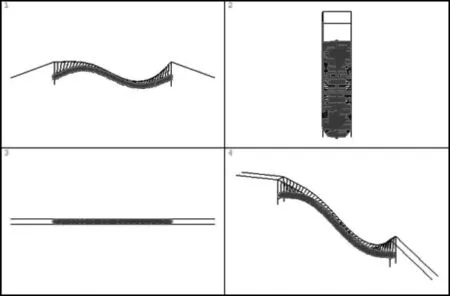
主梁反对称竖弯
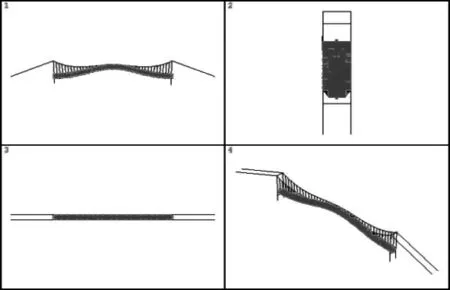
主梁正对称竖弯

主梁扭转

主梁二阶正对称竖弯

主梁反对称侧弯
根据频率及振型总结泸州长江二桥动力特性的特点为:1) 该悬索桥的振动频率与大型复杂结构的振动规律一致,即:各阶频率差值比较小,频率表现出聚集的现象。
2) 该桥基频f=0.122 0 Hz,T=8.19 s>5 s,周期较长,横桥向地震动响应最大时的自震周期为2.45 s,不会发生共振,这对该桥的抗震设计有利。
3) 刚开始出现的振型为主梁侧弯,这是因为一般侧向刚度最小,其次为竖弯。在第4阶才开始出现扭转振型,这与在横向采用了比较密集的横梁(每隔3.6 m)有关,使得桥梁的扭转刚度较大。
4) 扭转频率与侧弯频率比为0.322 2/0.122 0=2.65,而扭转振动是悬索桥颤振的主要形态,该桥扭弯比大于1.5,符合稳定要求。
5) 振型先开始出现规律的振型,如单纯的主梁、主缆振动,之后开始出现梁、主缆共同振动的耦合现象,阶数越高耦合现象越严重。
5 抗风性能计算
本桥位于开阔水面以上,地面粗糙度类别按A类考虑,桥面基准高度为45.5 m,可计算得出加劲梁用于颤振稳定性验算的设计基准风速V=34.2 m/s。由《公路桥梁抗风设计规范》6.3.8条,风速脉动修正系数μf为1.22,则计算得加劲梁颤振检验风速[Vcr]为50.1 m/s。
根据《公路桥梁抗风设计规范》6.3.1条,颤振稳定性指数应该按下述公式计算:

本桥的颤振稳定性指数为2.08,小于2.5,按照6.3.3条规定,当颤振稳定性指数If<2.5时,可按第6.3.4条规定计算桥梁的颤振临界风速。本桥由于加劲梁且有较大的抗扭刚度,计算得到的颤振稳定性表明本桥具有抗风稳定性,按《公路桥梁抗风设计规范》计算得到的临界风速值为114.9 m/s,远大于颤振检验风速,满足相关规定。桥梁的风振特性有待下阶段进行专项的抗风性能研究。
6 结语
该文利用有限元分析软件ansys对大跨度悬索桥进行建模,明确了地锚式悬索桥恒载和缆索系统初应力对悬索桥模态的影响,其中恒载的影响与自锚式悬索桥有很大区别。总结了泸州长江二桥动力特性特点。并由规范理论上验证了悬索桥具有良好的抗风性能。
[1] 李廉锟.结构力学[M].北京:高等教育出版社,2010.
[2] 刘忠平,戴公连.自锚式悬索桥有限元建模及动力特性影响因素研究[J].中外公路,2007(8).
[3] 彭大文,陈昀明.钢筋混凝土加劲桁架悬索桥的模态分析[J].地震工程与工程振动,2001(4).
[4] JTG/T D60-01-2004,公路桥梁抗风设计规范[S].
[5] 范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[6] 中南大学土木工程学院.长沙市三汊矶湘江大桥主桥设计研究总报告[R].2004.
[7] 王新敏.ANSYS 工程结构数值分析[M].北京:人民交通出版社,2007.
1008-844X(2016)04-0068-03
U 448.25
A

