基于机会约束规划的汇流风电场穿透功率极限计算

高正平，赵宏大，王哲，戴琦，陈永祥

（1.国网江苏省电力公司电力经济技术研究院，江苏南京 210009；2.河海大学能源与电气学院，江苏南京 211100）

基于机会约束规划的汇流风电场穿透功率极限计算

高正平1，赵宏大1，王哲1，戴琦1，陈永祥2

（1.国网江苏省电力公司电力经济技术研究院，江苏南京 210009；2.河海大学能源与电气学院，江苏南京 211100）

大规模的风力发电并网给电网的运行与稳定带来了一系列的问题，研究风力发电的穿透功率极限对于风力发电并网的规划以及运行有着重要意义。基于随机规划理论，利用拉丁超立方采样（latin hypercube sampling，LHS）处理汇流风电场的相关性风速数据，提出了汇流风电场穿透功率极限计算方法，计算中考虑了在同一汇流点不同风电场的风速随机性和相关性，计算得到含有汇流风电场发电系统的线路潮流，进一步基于机会约束规划，利用改进的粒子群算法计算得到汇流风电场的穿透功率极限。在IEEE30系统算例上验证了计算方法的有效性，并简要分析了风力发电位于不同接入点对穿透功率极限的影响。

汇流风电场；穿透功率极限；机会约束规划；拉丁超立方采样；改进粒子群算法

面对日益严重的能源危机和环境恶化等问题，如何开发并利用新能源成为各国面临的新课题。目前，风力发电技术作为最为成熟的可再生能源发电方式，正处于快速发展的时期并已经得到大范围的商业化应用，而大型风电场发电并网已经成为风电并网的主要模式[1]。根据对江苏省沿海风电场分布情况的分析知，目前风电分布呈现出大规模汇流接入、风带内多个风电场输出功率之间存在互补效应等新特点。另外，风能本身具有随机性与间歇性，大规模风电场接入电网之后，必然会对电力系统的运行提出新的要求。

风电穿透功率极限是指系统所能够接受的最大风电装机容量占系统最大负荷的百分比[2]。大型风电场发电并网必然会对电力系统产生很多的影响[3-4]，因此，计算合理的接入容量具有非常重要的参考价值，能够对风电的开发和消纳产生积极的促进作用。对于穿透功率极限的计算并没有统一的方法，目前国内外学者一般采用较成熟的智能算法对带约束的穿透功率极限计算模型进行优化。文献[5]首次引入机会约束规划（chance constrained programming，CCP）理论，提出基于随机优化技术的风电准入容量计算模型。文献[6-7]在考虑风速随机性和相关性的基础上，分别运用基于随机模拟技术的智能优化算法，计算得到风电的最大准入容量。

本文进一步完善了风电穿透功率极限的计算模型，考虑了以汇流方式接入的风电场之间的风速波动特性和互补特性，利用拉丁超立方采样得到汇流风电场的相关性风速数据，建立了汇流风电场穿透功率极限的机会约束规划模型，并采用改进的粒子群算法求解模型。以IEEE-30系统作为算例进行了验算，验证了本方法的有效性。

1 汇流风电场的时空分布特性

1.1 时延性和相关性

本文研究的汇流站多风电场在空间位置上位于江苏沿海一带，具有沿同一风带依次分布的特点，在同一风向的作用下，其风速和功率具有明显的时间上的延迟和大小的递减等特点。通常情况下，多风电场的相关性可以采用Pearson线性相关系数作为度量的指标[8]。但Pearson线性相关系数会因为时延的影响发生显著变化，如图1所示。

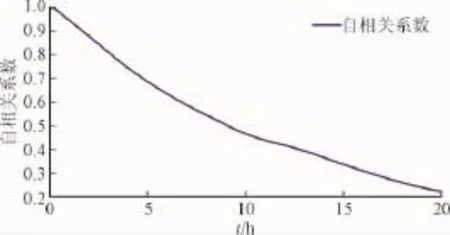
图1 单风电场输出功率自相关系数随时延变化曲线Fig.1 Auto-correlation functions of wind speed with different shifted times

所以，在研究多风电场风速相关性时，需要考虑时延对相关性的影响。假定在一段时间内，多风电场受同一风带影响，风向基本不变。对于任意给定的一组风电场（同一风带上的2个风电场）的风速序列（Xt，Yt）在时延时间T下的互相关系数RXY，计算公式为[9]：

其中，

式中：T为延时时间；XM、YM为风速序列Xt和Yt的平均值；n为风速序列样本总数。

根据式（1）就可以得到多风电场风速的互相关系数随延时时间变化的曲线。根据本文的计算需求，能够根据实际汇流风电场之间的风速数据确定他们的最大互相关系数RXY。

进一步由风电场之间的最大互相关系数生成相关性矩阵：

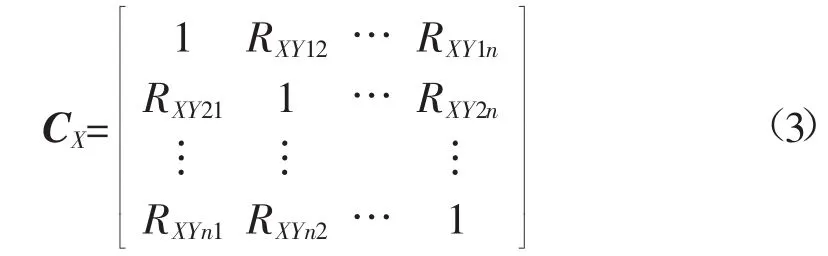
1.2 风电场出力特性

从长时间角度来看，风速服从威布尔分布（Weibull distribution）。威布尔分布的概率密度方程为：

式中：v为实际风速；k为形状参数；c为尺度参数。

风电机组的输出功率与风速的关系可由式（5）所示的分段函数简化表达：

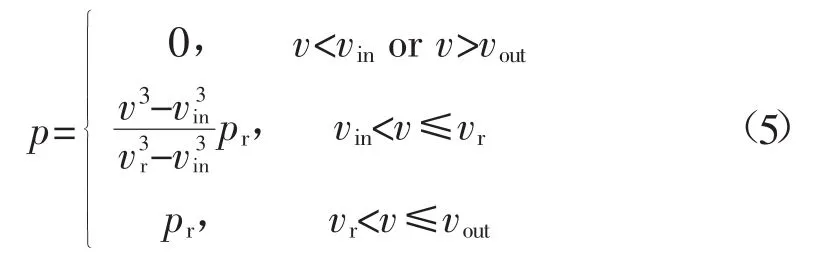
式中：v为实际风速；vr为风机额定风速；vin、vout分别为切入风速和切出风速；pr为机组额定功率。由式（5）可以看出，当风速小于vin或大于vout时，风机输出功率为0，与电网解列。

2 汇流风电站准入模型的建立

CCP用于解决的一类随机规划问题一般具有2个特点，一是约束条件中含有随机变量；二是在做出决策之前随机变量通常难以观测到。即所作决策应该使约束条件成立的概率在不小于人为设定的置信水平的同时，得到最优化的目标函数[10]。

本文在考虑风速相关性、波动性的基础上，建立了基于机会约束规划的汇流风电场穿透功率极限计算模型。在计算时，以系统潮流的等式约束及不等式约束为前提，选取各个风电场装机容量和部分常规机组的有功出力作为决策变量进行优化调整，最后以系统可接纳的各风电场装机容量的总和作为目标函数。

1）模型的目标函数为：

2）约束条件为。等式约束包括系统有功、无功功率的平衡。不等式约束条件分为决策变量和状态变量。决策变量为各风电的装机容量、常规发电机组的有功。状态变量本文主要考虑常规发电机组的无功出力、节点电压幅值、线路潮流上下限、系统频率偏移量，各个变量约束条件为：

式中：Pgi、Qgi分别为常规机组的有功和无功出力；PLi、 QLi分别为节点有功与无功负荷；为风电机组的有功出力；Pli为第i条线路上的潮流；Ui为系统各节点电压的幅值；α1～α3分别为不等式约束相应的置信水平，即约束条件允许越限的概率，取值在0.9～1.0之间。取值越大，表明计算的结果越趋于保守。Δf为系统频率偏移量，可由系统的静态频率特性计算得到：Δf=ΔP/（∑KG+KL）。其中，ΔP为系统有功功率的不平衡量，KG、KL分别为发电机单位调节功率和负荷单位调节功率。

3 基于随机模拟技术的粒子群算法

3.1 LHS采样

拉丁超立方采样是一种分层采样方法，由M.D.Mckay等学者在1979年提出[11]。与普通的随机采样相比，LHS采样最明显的优点在于在采样数相等的情况下，能够更完整地覆盖采样区域。

传统的LHS方法主要用于对相互独立的随机变量进行采样，具体过程是改变各个随机变量采样值的排列顺序，从而使采样值之间的相关性趋于最小。采用的排序方法主要有Cholesky分解法、Gram-Schmidt序列正交化方法[12-13]等。文[14]提出了一种利用LHS采样获取相关性样本的方法，并严格证明了使用该方法得到的采样值能够满足原本随机变量之间所具有的相关性。

在已知风电场风速的概率分布以及得到风速相关系数矩阵的前提下，利用LHS可以得到具有相关性的风速样本数据。利用Cholesky方法获取相关性样本的具体步骤如下：

1）根据文献[15]给出的经验式（8），可由输入的随机变量X相关系数矩阵CX，得到修订的相关系数矩阵CZ。

式中：随X的分布不同，T（ρij）的表达式也不一样。当随机变量X服从威布尔分布时，T（ρij）近似满足以下关系：

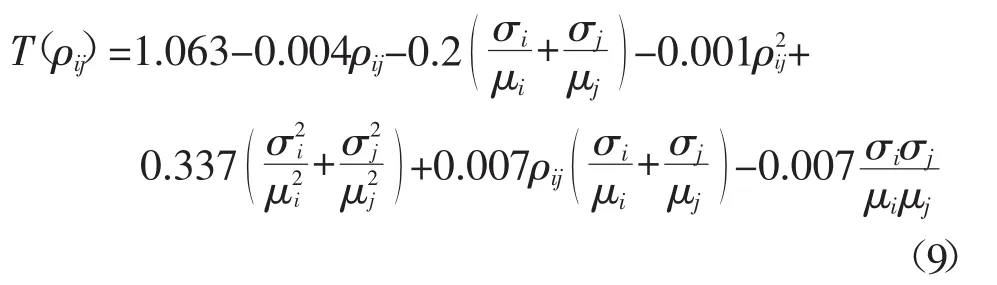
计算得到的修正矩阵CZ一般为正定对称矩阵，进一步可以对CZ进行Cholesky分解，得到下三角矩阵B，即：

式中：B即为所求的下三角矩阵。

2）对相互独立的n个标准正态随机变量利用随机采样方法得到样本矩阵W，由文献[14]的证明可知Z=BW的相关性矩阵亦为CZ，进一步由矩阵Z得到顺序矩阵LS。

3）对需要采样的n个输入变量X进行LHS采样，并根据顺序矩阵LS进行排序，最终得到样本矩阵S。

LHS采样方法具体如下：把Fk的取值空间均分为N等份，在每个区间中随机选取一个数作Yk的采样值，则Xk的采样值为：

式中：N为样本总数；Fi为第i个风电场的风速累积概率分布函数；xij为第i个风电场的第j个风速样本；uij为[0，1]上的均匀分布随机数。

3.2 改进粒子群算法

PSO算法是一种进化计算技术，源于Eberhat和Kennedy二人对鸟群捕食的行为研究。该算法本身具有良好的稳定性，并且由于简单而容易实现、不需要调整过多的参数以及计算速度快等诸多优点，已被广泛地应用在各个研究领域[16-17]。

原始的PSO算法存在容易早熟，并且在算法后期容易在全局最优解附近产生振荡等缺点。因此本文采用线性调整的方式改变ω值，ω与算法迭代次数的关系公式为：

式中：ωmax、ωmin分别为ω的最大值和最小值；k为当前迭代次数；kmax为最大迭代次数，通常取ωmax=0.9、ωmin=0.4。

为了平衡粒子的全局与局部搜索能力，取得优良的算法性能，引入收缩因子φ，以有效地控制粒子的飞行速度，其表达式为：

其中C=c1+c2，且为保证算法的顺利求解，C的值必须大于4。改进后的速度及位置更新公式为：

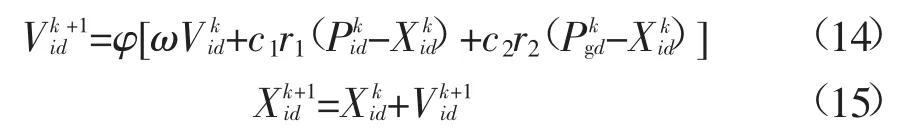
同时为防止粒子盲目搜索，将其位置和速度限制在一定的范围之内[－Xmax，Xmax]、[－Vmax，Vmax]。速度更新可根据式（16）进行修正：

搜索空间与最大速度的关系为：

基于机会约束规划的PSO算法流程见图2。

4 算例及结果分析

本文在Matlab-2010b平台上编写汇流风电场穿透功率极限计算程序，以IEEE-30系统作为算例，其网络结构如图3所示。IEEE-30节点有30个节点，41条线路，6个发电机，系统的总负荷为283.4 MW。

假设2号、5号常规机组保持额定出力不变，出力分别为58 MW和25 MW；将8号、11号、13号发电机的有功出力和汇流站的2个风电场的装机容量作为决策变量组成粒子参与优化。常规发电机组有关技术参数如表1所示；电压约束参数如表2所示，PV节点一般是有一定无功储备的发电厂或者具有可调无功电源设备的变电，因此将电压波动范围限制得比PQ节点更小。系统频率以±0.2 Hz为最大变化范围。

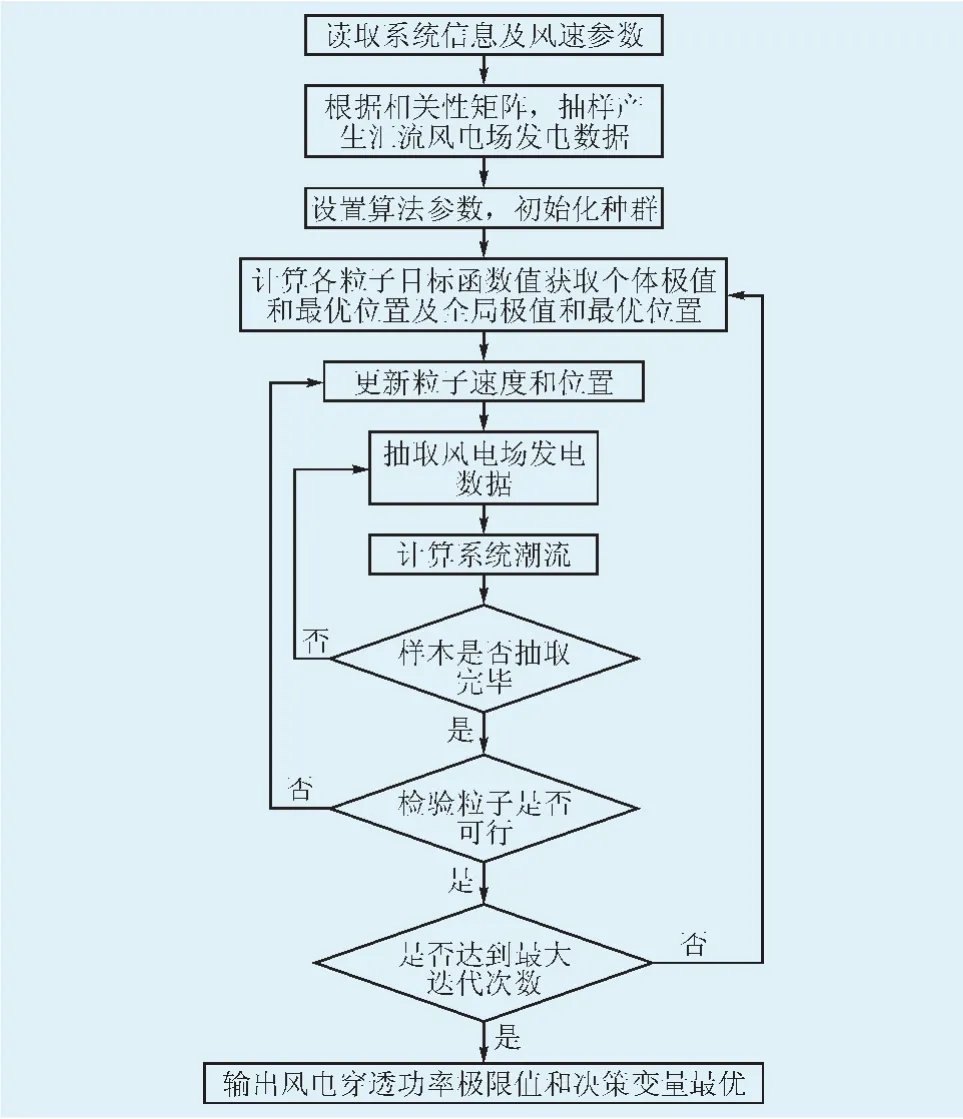
图2 基于机会约束规划的PSO算法流程Fig.2 Flow chart of PSO algorithm based on chance-constrained programming

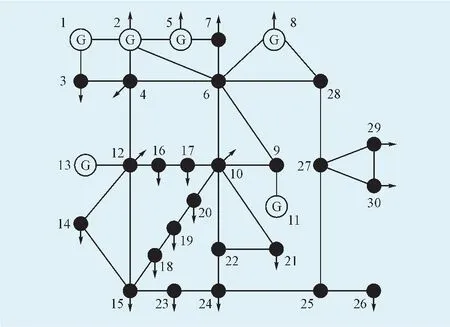
图3 IEEE-30测试系统Fig.3 Test system of IEEE30

表1 常规发电机组参数Tab.1 Parameters of conventional generators

风电机组的额定功率为1.5 MW，额定风速为15 m/s，切入风速为3 m/s，切出风速为24 m/s。不考虑风电机组的无功功率，设定机组以恒功率因素方式运行，功率因数为1。

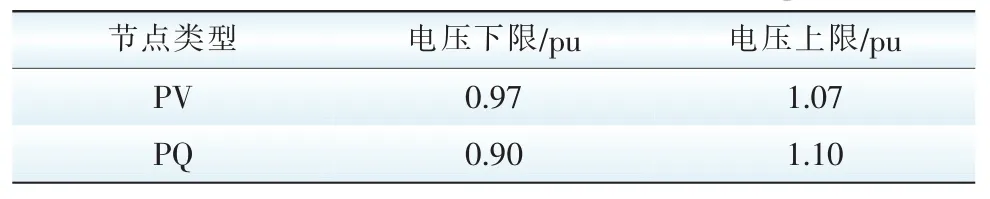
表2 节点电压参数Tab.2 Parameters of the node voltage

以2个风电场的汇流风电站为例，利用Matlab中的wblfit函数对实测的汇流站内的2个风电场1 a的风速数据进行威布尔分布参数拟合，计算得到威布尔参数c和k分别为7.025 5、2.315 4，7.699 4、2.191 3。为简化计算，本文以统计得到的2个风电场的最大互相关系数RXY=0.813描述风电场风速的相关性矩阵：

为了简化试验，将各约束的置信水平设置为相同数值，例如α1～α3=0.95。汇流风电场在同一点接入，计算得到不同置信水平下的最大穿透功率极限值如表3所示。

表3 不同置信水平下的穿透功率极限Tab.3 Power penetration limit at different confidence levels

表3的计算结果表明，当置信水平的取值变大时，汇流风电场穿透功率极限值将明显降低，原因是当置信水平的值趋向1时，模型考虑了某些发生概率很低的风速情况，如风电场同时满发的情况。这种情况下计算的结果更加趋于保守，等效到实际风电场规划的过程中，将直接关系到风电场建设的经济性。即计算的结果越是保守，则需要更多的投入以保证电网的稳定运行。

表4列出了风速相关性对于穿透功率极限的影响，考虑相关性时相关系数取0.813，独立时相关性系数取0，置信水平取值0.95。可以看出，在考虑风速相关性的情况下，穿透功率极限值明显变小，其原因是当风速相关时，2个风电场出力叠加时，波动量比不考虑相关性时要大很多。

为考察不同地点接入电网对穿透功率极限的影响，风电场接入电网采用同一地点集中接入与分散接入方式，置信水平取相同值0.95。计算得到的穿透功率极限值见表5。

表4 不同风速相关性下的穿透功率极限Tab.4 Power penetration limit at different wind speed correlation

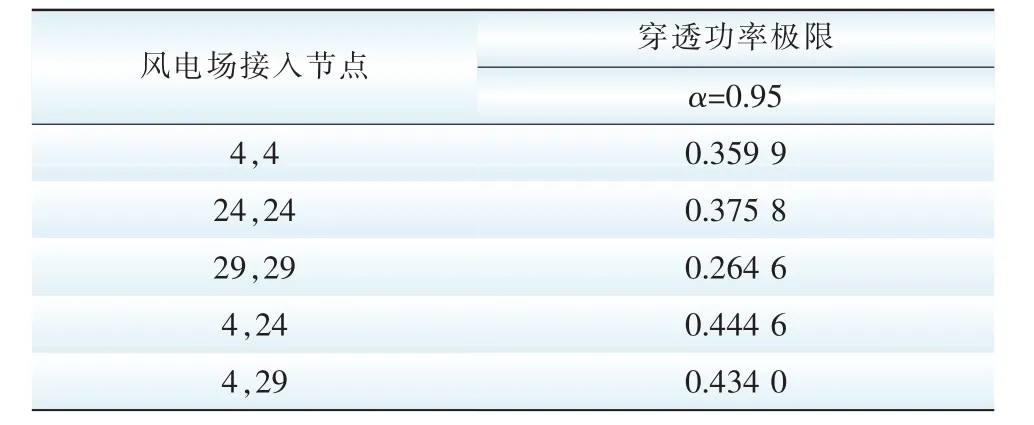
表5 不同接入方式下的穿透功率极限Tab.5 Power penetration limit at different access modes

由表5可知，当风电场以不同方式接入系统时，穿透功率极限明显不同。风电接入地点以及风电接入形式（分散或者集中）都会显著影响穿透功率极限的大小。可以看出，当风电场分散接入系统时，穿透功率极限明显比在同一地点集中接入时要高，即汇流风电场的穿透功率极限比分散电场的要低；而当风电接入地点距离常规发电机组较远、处于系统网络薄弱环节时，穿透功率极限也会显著降低。因此，在对风电场进行前期规划时，首先要综合分析系统的网络结构以确定各个候选接入点，进而核算每一个接入点的穿透功率极限，最终确定合理的风电接入位置、接入形式以及各个风电场的最大装机容量。

表6列出了几种接入方式下各个约束条件的越限概率，可以看出当风电接入方式不同时，各约束条件越限情况也有所不同。当汇流风电场接入点处于网络送端，穿透极限主要受系统频率的制约。当风电位于网络受端，主要受节点电压的影响。

表6 约束条件越限概率Tab.6 The probability of system constraint violation

5 结论

穿透功率极限计算对于风电规划发展具有重要的意义，在进行穿透功率计算时需要考虑多方面的影响，包括风电分布形式、接入地点以及系统网络结构。本文基于机会约束规划模型，考虑了潮流约束及风电的相关性、随机性，提出了一种汇流风电场穿透功率极限计算方法，对于大型风电汇流站的规划建设具有一定的指导意义。同时通过分析得出结论，风电场位于网络送端、受端时制约穿透极限大小的因素分别为系统频率和节点电压。

[1]张志春，刘洪伟.我国发展风电产业的战略性分析[J].电网与清洁能源，2013，29（5）：67-72．ZHANG Zhichun，LIU Hongwei.Strategic analysis of wind power industry development in China[J].Power System and Clean Energy，2013，29（5）:67-72（in Chinese）.

[2]廖萍，李兴源．风电场穿透功率极限计算方法综述[J]．电网技术，2008，32（10）：50-53．LIAO Ping，LI Xingyuan.A survey on calculation methods of wind power penetration limit[J].Power System Technology，2008，32（10）:50-53（in Chinese）.

[3]范李平，杨力森，武粉桃.风电场并网对电力系统稳定性影响[J].电网与清洁能源，2009，25（6）：58-61.FAN Liping，YANG Lisen，WU Fentao.Influence of wind farm interconnected to power grid on stability of power system[J].Power System and Clean Energy，2009，25（6）: 58-61（in Chinese）．

[4]朱涛.风电接入系统的相关问题研究综述 [J].南方电网技术，2009（5）:58-63.ZHU Tao.Review of some problems related to wind farm integration[J].Southern Power System Technology，2009（5）:58-63（in Chinese）.

[5]雷亚洲，王伟胜，印永华，等．基于机会约束规划的风电穿透功率极限计算[J]．中国电机工程学报，2002，22（5）：32-35．LEI Yazhou，WANG Weisheng，YIN Yonghua，et al.Wind power penetration limit calculation based on chance constrained programming[J].Proceedings of the CSEE，2002，22（5）:32-35（in Chinese）.

[6]徐玉琴，张林浩．考虑风速相关性的风电接入能力分析[J]．可再生能源，2014，32（2）：201-206．XU Yuqing，ZHANG Linhao.Analysis on wind power penetration limit considering wind speed correlation[J].Renewable Energy Resource，2014，32（2）:201-206（in Chinese）.

[7]汤雪松，殷明慧，邹云．考虑风速相关性的风电穿透功率极限的改进计算[J]．电网技术，2015，39（2）：420-425．TANG Xuesong，YIN Minghui，ZOU Yun.An improved method to calculate wind power penetration limit considering wind speed correlation[J].Power System Technology，2015，39（2）:420-425（in Chinese）.

[8]唐志伟，李国杰，孙旭日，等．风电功率相关性分析[J]．电工电能新技术，2014（5）：69-75．TANG Zhiwei，LI Guojie，SUN Xuri，et al.Wind power correlation analysis[J].Advanced Technology of Electrical Engineering and Energy，2014（5）:69-75（in Chinese）.

[9]BECHRAKIS D A，SPARIS P D.Correlation of wind speed between neighboring measuring stations[J].IEEE Transac-tions on Energy Conversion，2004，19（2）:400-406.

[10]刘宝碇，赵瑞清．随机规划与模糊规划[M]．北京：清华大学出版社，1998：74-94．

[11]MCKAY M D，BECKMAN R J，CONOVER W J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J].Technometrics，1979，21（2）:239-245.

[12]于晗，钟志勇，黄杰波，等．采用拉丁超立方采样的电力系统概率潮流计算方法[J]．电力系统自动化，2009，33（21）：32-36．YU Han，ZHONG Zhiyong，HUANG Jiebo，et al.A probabilistic load flow calculation method with Latin hypercube sampling[J].Automation of Electric Power Systems，2009，33（21）:32-36（in Chinese）.

[13]YU H，CHUNG C Y，WONG K P，et al.Probabilistic load flow evaluation with hybrid latin hypercube sampling and choleskydecomposition[J].IEEE Transactionson Power Systems，2009，24（2）:661-667.

[14]陈雁，文劲宇，程时杰．考虑输入变量相关性的概率潮流计算方法[J]．中国电机工程学报，2011，31（22）：80-87．CHEN Yan，WEN Jinyu，CHENG Shijie.Probabilistic load flow analysis considering dependencies among input random variables[J].Proceedings of the CSEE，2011，31（22）:80-87（in Chinese）.

[15]LIU P L，DER KIUREGHIAN A.Multivariate distribution modelswith prescribed marginalsand covariances[J].Probabilistic Engineering Mechanics，1986，1（2）:105-112.

[16]KENNEDY J，EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Perth，WA，Australia:IEEE，1995: 1942-1948.

[17]王锐，顾伟，孙蓉，等．基于概率最优潮流的风电接入能力分析[J]．电网技术，2011，35（12）：214-220． WANG Rui，GU Wei，SUN Rong，et al.Analysis on wind power penetration limit based on probabilistically optimal power flow[J].Power System Technology，2011，35（12）: 214-220（in Chinese）.

（编辑 董小兵）

Power Penetration Limit Calculation of Converged Wind Farms Based on Chance-Constrained Programming

GAO Zhengping1，ZHAO Hongda1，WANG Zhe1，DAI Qi1，CHEN Yongxiang2
（1.State Grid Jiangsu Electric Power Company Economic Research Institute，Nanjing 210009，Jiangsu，China；2.College of Energy and Electrical Engineering，Hohai University，Nanjing 211100，Jiangsu，China）

Integration of large-scale wind power brings a series of problems to the operation and stability of the power system，so research on the wind power penetration limit is of great significance for wind power generation and network planning and operation.This paper presents a method to calculate the power penetration limit of converged wind farms based on stochastic programming theory and Latin hypercube sampling is used to simulate the correlated wind speeds of converged wind farms.Considering randomness and correlations of the wind speed between converged wind farms，it analyzes the load flow of the power system with converged wind farms and further uses chance-constrained programming and particle swarm optimization to calculate power penetration limit.Finally，taking the IEEE 30-bus system as an example shows the calculation method is effective，and different access points that impact on the power penetration limit are analyzed.

converged wind farms；power penetration limit；chance-constrained programming；Latin hypercube sampling；improved particle swarm optimization algorithm

2015-11-20。

高正平（1976—），男，博士，高级工程师，主要研究方向为电网企业运营监测、采购与供应链管理、电网工程技术经济；

陈永祥（1989—），男，硕士研究生，研究方向为新能源并网规划与运行。

1674-3814（2016）05-0128-06

TM715

A

国家自然科学基金项目（51422701）。

Project Supported by the National Natural Science Foundation of China（51422701）.