基于解卷积的网络优化算法研究及应用*

哈尔滨医科大学卫生统计学教研室（150081） 王文杰 谢宏宇 侯 艳 李 康

基于解卷积的网络优化算法研究及应用*

哈尔滨医科大学卫生统计学教研室（150081） 王文杰 谢宏宇 侯 艳 李 康△

目的探讨网络解卷积算法对网络结构的优化效果。方法模拟研究采用四种网络算法对具有金标准的DREAM 5平台数据进行网络构建，并评价解卷积优化前后的网络准确性。实例研究使用RF回归对卵巢癌晚期化疗敏感性患者的基因表达数据构建网络，再通过网络解卷积算法优化。结果模拟研究结果表明，四种网络构建方法推断出来的网络结构在解卷积算法优化后，其准确性均有不同程度的提高，其中基于线性相关的网络构建方法提高幅度明显大于CLR和RF算法；实例分析结果表明，采用RF－ND方法构建的网络移除了部分间接边，其优化后能得到与现有数据库较为一致的网络结构。结论应用解卷积算法能够优化不同网络构建方法得到的网络，实际中能得到准确度较高的网络结构。

调控网络 解卷积 网络优化

网络研究能够直观地反映变量间的作用关系，有助于特征标志物的筛选，并能从分子水平阐述复杂的生物过程，因此成为了近年的研究热点之一。目前有很多基因调控网络的构建方法，如基于变量间相关或偏相关系数的方法，计算变量间信息熵的互信息法，基于图形及信息传递的高斯图论模型，以及基于因果概率的贝叶斯网络模型等［1－4］。由于高维组学数据变量间具有复杂的关联传递效应，一般的网络构建方法很难识别出变量间真正的直接调控关系，如由于A→B→C→D强相关，使得A→C、A→D这种本身并无真正调控关系的间接边也表现出强相关（图1左）；或者由于A→B→D和A→C→D的两个传递效应，使得A→D的关系增强（图1右）。随着网络中变量个数的增多和级联关系的增加，这种由传递效应产生的间接边会随之增加，容易出现假阳性结果，使得网络推断的准确性大幅降低。本文引入一种基于解卷积的网络优化算法，可以进一步优化推断出来的网络结构，移除间接边，解决上述问题。

图1 四个节点在两种传递效应机制下的网络构建可能出现假阳性结果

原理与方法

网络解卷积算法是一种网络优化方法，其基本思想是：根据不同网络推断方法（如Pearson相关系数）得到网络结构数据，建立一个网络拓扑图的邻接矩阵Gobs，并将其分解为具有直接关联和各种长度的间接关联矩阵之和，即

而Gindir根据关系矩阵的传递闭包运算有

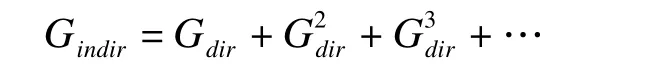
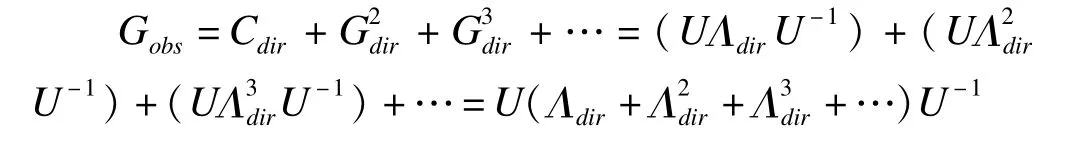
其中U和U－1分别为直接关联矩阵Gdir的特征向量矩阵及其逆阵，Λdir为相应特征值的对角矩阵。通过对关联矩阵进行线性尺度变换，可以将所有特征值的取值范围限定在1至－1，可以根据无穷泰勒级数，导出近似公式：

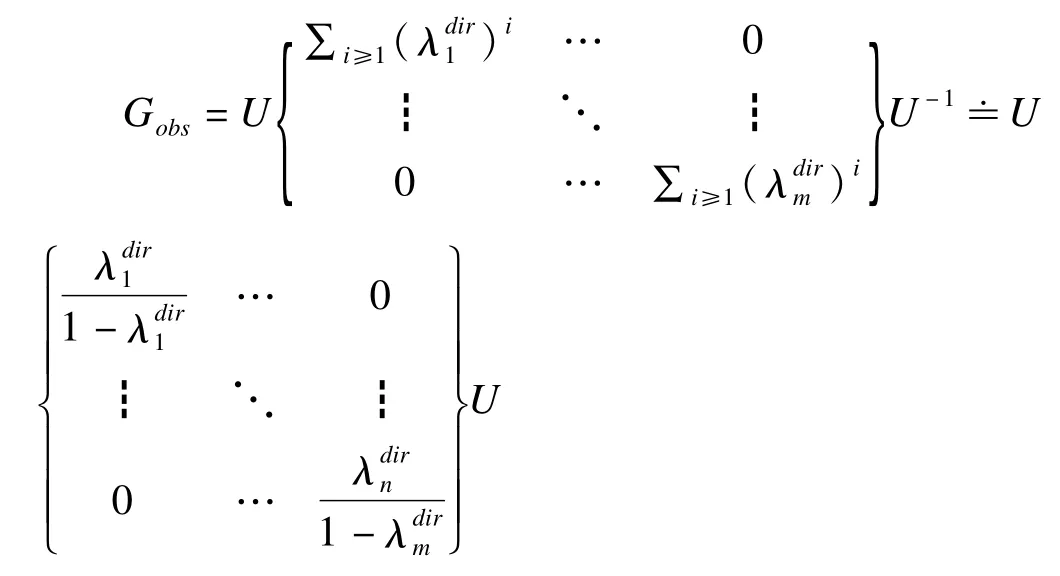
实际数据获得的关联矩阵同样可以分解为

上述基于特征分解的网络解卷积运算需满足两个假设：间接边权重等于直接边权重的乘积；观察到的边权重等于直接边和间接边之和。Feizi研究证明，理想情况下，当网络结构的所有边完全满足这两个假设时，基于特征分解的解卷积运算能移除所有间接边；而当网络结构不全满足假设时，该算法也能准确推断出87%的直接边［5］。

网络解卷积算法先通过对网络结构图的邻接矩阵的特征分解，利用无穷泰勒系数和，最终完成对网络各边权重的重新赋值。通过限定一个阈值，可以把权重较高，置信度较强的边筛选出来。从而可以移除间接边，准确推断出直接网络结构。

模拟研究

1．研究目的

使用解卷积算法对四种不同的网络构建方法得到的网络进行优化，并评价其效果。四种方法分别采用基于Pearson相关系数、Spearson相关系数、互信息的环境相关似然度算法（context likelihood of relatedness，CLR）及随机森林回归算法。对三组数据进行网络构建，然后应用解卷积算法优化，得到优化后的网络结构，最后评价解卷积算法优化前后的效果。

2．数据来源

使用基因逆向工程评估与方法对话平台（dialogue on reverse engineering assessment and methods project，DREAM）的数据进行评价。该平台用于评价网络推断性能的数据主要包括In silico、E．coli和S．cerevisiae等，其中In silico是通过Genenetweaver软件模拟出来的具有金标准的调控网络数据，其余两个是用生物学实验测序得到的调控网络数据［6］。

表1 DREAM 5网络数据验证平台

3．评价指标

（1）ROC曲线下面积AUC，即综合评价真阳性率和假阳性率的指标。其中真阳性率也称回召率，即TPR（k）＝TP（k）/P，TP（k）为网络算法得出的k条边在与金标准比较后正确边的数量，k值可根据网络构建时选择不同的阈值而改变，P为金标准中阳性边的数量。假阳性率为FPR（k）＝FP（k）/N，FP（k）为网络算法得出的k条边在与金标准比较后错误边的数量，N为金标准中阴性边的数量。FPR（k），c为根据构建网络的阈值得到的网络边数。

（2）准确度－回召率曲线下面积（area under the precision－recall curve，AUPR），即综合评价准确度和回召率的指标。准确度为PRE＝TP（k）/k，即网络算法得出的k条边中正确边的比例。

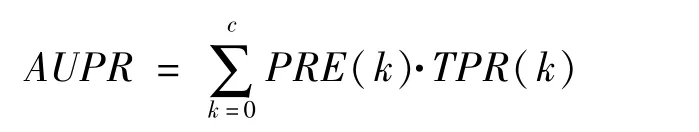
4．网络优化的评价结果

四种网络构建方法、三组网络数据的评价结果如表2。结果显示：对于三组不同的网络数据，其还原程度不尽相同，In silico的AUROC与AUPR均最高，表明构造出来的网络结构相比另外两个更接近于金标准结构；对于四种不同的网络构建方法，基于随机森林回归算法的AUROC，AUPR均比其他构建方法要高，尤其是在In silico数据集上表现远高于其他算法，ROC值达到0．815，显示了该方法良好的网络重构性能；对于不同的网络构建方法，解卷积优化前后其AUROC，AUPR在三个数据集上均有不同程度的提高。总体而言，经由解卷积算法优化后，基于相关的网络构建方法，其AUROC与AUPR的提高幅度明显大于CLR和RF算法。

表2 不同网络构建方法及不同数据，解卷积优化前后性能比较

实例分析

本研究通过对卵巢癌晚期化疗患者的基因表达数据进行分析，使用RF回归方法构建网络，再通过网络解卷积算法优化，得出基因间的调控关系网络。最后，结合生物学知识、通路数据库及文献查询，对网络进行生物学解释，从基因组学的角度，为卵巢癌化疗敏感性的生物学机制研究提供依据。

本研究从TCGA数据库下载348例基于卡铂－紫杉醇化疗方案的晚期卵巢癌患者的基因表达谱数据，根据化疗药物反应的敏感程度分为化疗药物敏感组310例和化疗药物不敏感组38例。全基因组表达谱数据一共测得12042个基因的表达值，使用基于W ilcoxon秩和检验的置换检验，进行1000次置换，筛选出P＜0．05（校正后）的基因431个，并将这部分数据进行KEGG通路富集分析，结果有10个基因显著富集在Wnt信号通路以及溶酶体通路。对所富集的10个基因的表达数据，采用RF回归方法构建网络，通过置换检验方法确定网络阈值，经100次随机置换后的VIM值的99%分位数为0．1148，从而确定边数目的阈值为c（VIM）＝0．1148，获得20条可能具有调控关系的边，网络结构如图2左所示。再通过网络解卷积算法对这20条边所构成的网络进行优化，重新对各边权重赋值，经由置换检验得到的新阈值为0．2016，获得16条关系边，移除了4条边，解卷积优化后的网络结构如图2右所示。

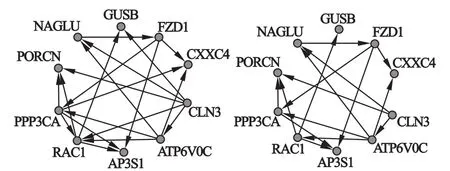
图2 卵巢癌患者化疗敏感性相关的基因调控网络解卷积前后结构（左为ND前，右为ND后）

通过查询GeneMANIA及KEGG基因数据库，发现这10个基因中，有8条边出现在数据库中。例如ATP6V0C调控NAGLU、CLN3、RAC1和PPP3CA四个基因。NAGLU和CLN3两个基因与ATP6V0C同属于溶酶体通路，RAC1、PPP3CA基因与ATP6V0C同属Wnt信号转导通路。并且已有文献报道ATP6V0C、NAGLU和CLN3基因在溶酶体的内吞以及物质转运过程中发挥重要作用［7］；ATP6V0C调控的RAC1和PPP3CA基因编码合成Wnt通路中重要的反应酶，参与调节多个细胞活动，如控制细胞生长、细胞骨架重组，以及激活蛋白激酶等［8－9］。该结果与随机森林回归构建的网络结构一致，对于这些重要的调控关系，基于随机森林回归的网络构建算法均能很好地还原出来，并且在经解卷积算法优化后，这些调控关系都得以保留。经由解卷积算法移除的4条边，即PPP3CA、RAC1、CLN3、GUSB基因间的间接调控关系，在数据库中均未查询到，并且暂时也无相应文献报道，这就体现了解卷积算法在移除间接调控关系的优化作用。而在剩余的边中，与ATP6V0C有关的基因还有CXXC4，此调控关系在geneMANIA并没有找到相应的调控关系，提示这一调控关系需要进一步研究。

讨 论

本文在简要介绍解卷积算法原理的基础上，通过DREAM 5数据验证平台的模拟数据，研究其对不同网络构建方法，不同网络数据集的优化性能。研究使用目前常见的四种基因调控网络构建方法：基于两种相关系数的网络分析方法，基于互信息的构建方法，基于随机森林（RF）回归的方法等。其中，基于线性相关的调控网络模型计算任意两基因表达水平的相关系数（Pearson或Spearman相关系数），对相关系数进行排序，进而构建出网络；基于互信息（M I）的方法主要通过计算变量间的边际概率和联合概率，从而得出变量间的互信息值，并根据其构建网络；基于随机森林回归的算法，通过回归树对每个目标基因都拟合了回归模型，计算出变量重要性评分（VIM），可得到两基因间调控关系的大小，并根据VIM值排序从而重建整个网络。最后将基于RF－ND的方法应用到实际卵巢癌化疗敏感性的基因表达数据，并作出生物学解释。关于网络解卷积优化方法的实际应用，需要注意以下几个问题：

1．本研究使用的网络解卷积算法是基于网络邻接矩阵的特征分解及无穷泰勒级数和得到，如果所优化的网络邻接矩阵不可进行特征分解，则无法继续使用本方法优化。这种情况下，可以使用基于迭代共轭梯度递减的算法来进行网络解卷积的优化运算［5，10－11］，其结合了共轭性和最速下降两种方法，不仅解决了一般网络结构优化问题，还可处理高维情况下的大型计算问题。

2．解卷积算法属于网络优化方法，最终得到的网络结构的准确性也受所选择网络构建方法的影响。在模拟研究中，四种网络构建方法所重构的网络结构，在解卷积优化后均有不同程度的提高，其中基于线性相关的方法优化幅度最大，其主要原因是线性相关类方法在衡量任意两基因间的相关性时，并未考虑其他中介基因存在时造成的间接传递效应，因此其构建出来的网络可能包含较多的假阳性间接边，而解卷积算法正好解决该问题，因此获得较佳的优化效果。而RF回归算法，在计算两变量间的VIM值时，考虑了其他变量的相互影响，构造出来的网络结构较为准确，因此其优化前得分本身较高，优化后提升幅度并不大，但总的准确度仍然最高。说明使用随机森林（RF）回归构建网络，再使用网络解卷积进行优化，即RF－ND方法，是一种值得推荐的网络构建方法。

3．使用RF－ND方法的最大特点是对变量的数目没有限制，可以在高维数据上构建网络，而且可以给出基因之间的调控方向。

4．由于实际基因组数据往往缺乏完整准确的调控关系（即金标准），因此仅基于目前的数据库和文献查询只能验证部分调控关系，用于评价一个构建方法的优劣本身并不够严谨全面，对此尚需进一步研究。另外，如何构造既包含差异基因也包含非差异基因的全局调控网络，还原生物体内完整的基因调控过程也极具挑战性。

［1］Tibshirani R．Regression shrinkage and selection via the lasso．J R Stat Soc Series B Stat Methodol，1996，58：267-288．

［2］Pesch R，Lysenko A，Hindle M，et al．Graph-based sequence annotation using a data integration approach．Journal of integrative bioinformatics，2008，5（2），doi：10．2390/biecoll-jib-2008-94．

［3］Butte AJ，Kohane IS．Mutual information relevance networks：functional genom ic clustering using pairw ise entropy measuerments，2000，5：418-429．

［4］Mani S，Cooper GF．A Bayesian local causal discovery algorithm，2004：731-735．

［5］Feizi S，Marbach D，Medard M，et al．Network deconvolution as a generalmethod to distinguish direct dependencies in networks．Nat Biotechnol，2013，31（8）：726-733．

［6］Stolovitzky G，Monroe D，Califano A．Dialogue on reverse-engineering assessment and methods：the DREAM of high-throughput pathway inference．Ann．NY Acad．Sci，2007，1115：1-22．

［7］You H，Jin J，Shu H，et al．Small interfering RNA targeting the subunit ATP6L of proton pump V-ATPase overcomes chemoresistance of breast cancer cells．Cancer Lett，2009，280（1）：110-119．

［8］Ji J，Feng X，ShiM，et al．Rac1 is correlated with aggressiveness and a potential therapeutic target for gastric cancer．Int JOncol，2015，46（3）：343-353．

［9］Dokmanovic M，Hirsch DS，Shen Y，et al．Rac1 as a potential therapeutic target for the treatment of target for thetreatment of trastuzumab-resistant breast cancer．Mol Cancer Ther，2009，8（6）：1557-1569．

［10］Horn R，Johnson C．Matrix analysis．Cambridge Univ Pr，1990．

［11］Faith JJ，Hayete B，Thaden JT，etal．Large-scalemapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles．PLoSBiol，2007，5（1）：e8．

（责任编辑：郭海强）

Network Optim ization Algorithm Based on Network Deconvolution and its Application

Wang Wenjie，Xie Hongyu，Hou Yan，et al
（Department of Health Statistics，School of Public Health，Harbin Medical University（150081），Harbin）

ObjectiveTo investigate the performance of the network optim ization based on network deconvolution．MethodsIn simulation studies，we performed four network reconstructionmethods to construct the gene regulatory network on the data from DREAM 5 platform which have contained the gold standard．Then we compared the accuracy of before and after optim ization based on network deconvolution algorithm．In pritical studies，we applied random forest regression to construct an original network on gene expression data which comes from the advanced ovarian cancer patients thatwas susceptible to chem ical therapy．Finally，we performed the network deconvolution method to optim ize the structure of it．ResultsSimulation studies demonstrated that the accuracy of networks that reconstructed by fourmethods was increased to some degree．For the range of improvement，method that based on linear correlation was greater than CLR and RF．In practice，themethod based on RF-ND removes some indirected edges and achieves satisfactory network structure that consistent to the existing database．ConclusionThe algorithm of network deconvolution could optimize the structure of network constructed by the differentmethods and obtain the network w ith higher accuracy．

Regulatory network；Network deconvolution；Network optimization

国家自然科学基金资助（81473072，81573256）；中国博士后基金资助（2015M571445）

△通信作者：李康，E-mail：likang＠ems．hrbmu．edu．cn