有序聚类分析及周期图法在猩红热流行周期中的应用研究*

段 禹黄晓磊王玉杰张俊青苏 虹潘海峰王 静△

·论著·

有序聚类分析及周期图法在猩红热流行周期中的应用研究*

段 禹1黄晓磊1王玉杰1张俊青2苏 虹1潘海峰1王 静1△

目的探讨合肥市猩红热的流行周期，为猩红热发病预测和早期预警提供理论基础。方法合肥市疾病预防控制中心提供1985－2003年猩红热病例资料的监测数据及2004－2008年网络直报监测数据。使用有序聚类分析对猩红热发病阶段划分类别，使用周期图法提取潜在周期并建立相应的周期函数拟合发病率资料。结果1985－2008年合肥市共有1996名猩红热病例，年平均发病率为1．9620/10万。24年猩红热发病率波动总体可按有序聚类分为低－高－低－高4个阶段，分别为1985－1988年，1989－1997年，1998－2003年，2004－2008年。其中前3阶段总和为19年，与周期图法检测出猩红热发病率序列存在的第一隐含周期T1＝19相同，此外序列还包含第二隐含周期T2＝5。结论有序聚类分析和周期图法可以运用于猩红热流行周期的识别和提取。

猩红热 流行周期 周期图法 有序样品聚类分析

猩红热是一种急性呼吸道传染病，由A组β型链球菌引起，为我国法定报告的乙类传染病［1］。猩红热感染者多为儿童、青少年［2］，引起的主要症状为发热、咽峡炎、全身弥漫性鲜红色皮疹和皮疹消退后明显脱屑［3］。目前，该病尚无特异性预防疫苗，同时抗生素滥用引起的链球菌耐药也为该病防治带来挑战［4］。了解猩红热的流行规律，预测其发病趋势对于控制该疾病的传播有着重要的作用。许多研究中已经应用统计学模型对传染病流行周期进行研究［5－6］，如：Lima等使用小波分析技术对于百日咳在智利的流行周期进行检测。本次研究旨在应用有序样品聚类及周期图法两种方式对合肥市1985至2008年猩红热流行规律进行分析，探讨其变化趋势及流行周期，并为猩红热发病预测，早期预警提供方法。

资料与方法

1．猩红热发病资料：合肥市疾病预防控制中心提供1985－2003年猩红热病例资料的监测数据及2004－2008年网络直报监测数据。猩红热病例的诊断按照国家卫生部颁布标准［7］，均为确诊病例，同时满足以下3条标准：（1）具有猩红热临床症状表现；（2）咽拭子或病灶分泌物血清学分群鉴定为A组β型链球菌；（3）猩红热相关的其他实验室检查出现阳性结果或具有可疑接触A组β型链球菌的流行病学史。合肥市各年的平均人口数由国家统计局获取，用于计算各年度的发病率（/10万）。

2．有序样品聚类：有序聚类算法是针对有序样本的一种统计分类方法。它将资料按照原有次序分为若干类别，属于特殊的条件系统聚类。其计算方法如下［8］：

（1）定义类的直径

长度为n的原始序列y中包含样本｛X（1），X（2），…，X（n－1），X（n）｝。将其按原有次序分为若干类别，设其中某一类G包含的样本有｛X（i），X（i+1），…，X（j）｝（j＞i），记为G＝｛i，i+1，…，j｝，则类别G的均值向量为：

定义类别G直径为：

直径D（i，j）表示类别G内共j－i+1个样本的总差异，其指标是离均差平方和。

（2）定义分类损失函数

用b（n，k）表示将n个有序样品分为k类的某一种分法，其中分割点分别为i1（i1＝1），i2，i3，…，ik，定义上述分类法的损失函数为：

损失函数L［b（n，k）］即为k个类别离均差平方和的总和，其越小表示该分类方式越优。当一种b（n，k）使分类损失函数L最小，将该分类法记为P（n，k）。

在将n个样品聚为k（1＜k＜n）类的过程中，首先通过上述公式（3）计算得到k＝2时最小损失函数L［P（n，2）］和此时的分割点，在此基础上增加1个新的最优分割点并计算出L［P（n，3）］，迭代该计算过程可以分别得到将n个样品聚为k（1＜k＜n）类的最优分法，以L［P（n，k）］为纵坐标，k为横坐标，画出损失函数变化趋势图，选择出最为合适的分类数。

3．周期图法：周期图法是一种使用试验周期配合实际序列，从而找出隐含周期的方法。若实际序列中确实存在频率为ωi的隐含周期，则周期图IN（ωi）在周期频率ωi处有较大的峰值，故我们可以借此判断序列中的潜在周期［9－10］。其计算方法如下：

（1）消除原始序列y的线性趋势

若长度为n原始序列y存在趋势或序列均值不为0，则需首先去除趋势成分H（t），调整后的序列为y1＝y－H（t）。

（2）计算傅里叶系数并检测隐含周期

其中t为序列中各项的期数，τ为试验周期，其取值范围为［1，n－1］的正整数，K为满足K×τ＜n的最大正整数，当τ使得达到最大时，t即为检测出的隐含周期Ti，需检验是否为周期震动的极大值（零假设：无周期震动）：

本次研究中取α＝0．05，其对应的J界值为2．996。若Ji小于等于界值，零假设成立，认为无周期震动，计算结束；若拒绝零假设，则认为T为相应的隐含周期，此时初相位：

振幅：

则周期为T的周期函数为：

（3）拟合周期函数

将序列y1代入步骤（2），计算出第一隐含周期及其周期函数C1（t）。随后，令y2＝y1－C1（t），并重复步骤（2），进一步提取第二隐含周期。同理可得yi＝yi－1－Ci－1（t），迭代该过程，直到J检验结果提示序列中不再存在周期震动。预测值Y（t）的95%置信区间采用bootstrap法进行估计［11］。对于原始样本y重复1000次样本含量为24的有放回抽样，从而得到1000个bootstrap样本，使用它们重新拟合上述线性函数和正弦函数模型，并利用模型计算相应的预测值。综合1000个bootstrap样本中的各期预测值的2．5分位数和97．5分位数作为Y（t）的95%置信区间的上下限。

4．统计学分析

使用样品有序聚类对于猩红热流行阶段进行分割；使用周期图法建立相应的周期函数拟合发病率资料，计算潜在周期；使用单位根检验（augmented dickey-fuller test，ADF）对猩红热发病序列进行平稳性检验。猩红热发病资料的计算处理，描述性统计分析，样品有序聚类与周期图法均使用MATLAB（version 7．0）编写程序实现。本次研究中检验水准α＝0．05。

结 果

1．猩红热发病率

合肥市24年共出现1996名猩红热病例，年平均发病率为1．9620/10万。2008年发病率最高，达到3．8317/10万，1987年发病率最低，达到0．5316/10万。发病率峰值分别出现在1991年、1995年、2005年、2008年，并依次增高。年发病率变化相对稳定，但自2003年以后总体呈现上升趋势（图1）。

2．1985－2008年基于猩红热发病率的有序聚类

将24年的猩红热发病率进行有序聚类，分别计算出将其聚为2～23类的最小损失函数，损失函数趋势图见图2。从图2可以看出，损失函数在4类时出现折点，随后下降趋势逐渐平稳，因此首先考虑将其聚为4类。24年聚成4类，损失函数值最小为5．7738，此时分割点分别为i1＝1，i2＝5，i3＝14，i4＝20。按照上述最优分法，24年可以划分为1985－1988年，1989－1997年，1998－2003年，2004－2008年四个阶段，其他具体分类信息可见表1。

图1 1985－2008年合肥市猩红热年发病率序列图（/105）

图2 1985－2008年合肥市猩红热发病率聚类最小损失函数随分组数量变化趋势图

表1 合肥市1985－2008年基于猩红热发病率的有序聚类分组

3．周期图法

从图1可以看出序列整体具有上升趋势，同时ADF检验结果显示t＝－0．2976＜－1．9507，P＝0．532，接受零假设，认为序列不平稳。因此使用detrend函数，去除原始序列中的线性趋势H（t），获得去除趋势后的发病率序列y1并再次进行检验（t＝－2．7628＞－1．9507，P＜0．01），显示y1序列平稳。利用y1＝y－H（t）求出线性趋势函数H（t）＝1．2306 +0．0585t。

随后，令y2＝y1－C1（t），并对y2再进行周期图分析，得出3．4100＞2．996，P＜0．05，第二隐含周期为5，其对应的周期函数为：

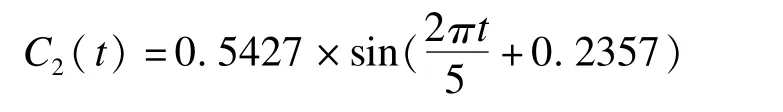
再次从y2中剔除周期函数C2（t）后得到y3。但对序列的周期检验结果显示J＝1．8496，P＞0．05，认为序列y3中无周期震动，故终止序列拟合。此时，将趋势项与两个周期函数线性相加得到序列的拟合函数Y（t），Y（t）与原始发病率序列的比较情况可见图3。

图3 1985－2008年合肥市猩红热发病率序列与周期图法拟合函数图

4．1985－2008年合肥市猩红热流行特点

周期图法的结果显示合肥市猩红热发病率波动的第一隐含周期为19年，这与有序聚类对其阶段的划分具有相同之处：第一阶段1985－1988年为周期函数C1（t）从低点开始上升至0的过程，随后第二阶段1989－1997年则是周期函数C1（t）位于x轴上方的阶段，第三阶段1998－2003年则是周期函数C1（t）处于极小值前后的年份。随后，周期函数C1（t）重新进入上升阶段，而此时则是有序聚类结果提示的第四阶段2004－2008年。前3个阶段总和为19年，与第一隐含周期相同。猩红热4个阶段的平均发病率呈现低－高－低－高的过程，与第一隐含周期的周期函数所展示的趋势相同。

讨 论

本次研究使用有序聚类分析及周期图法探讨了合肥市1985－2008年猩红热流行周期。猩红热年发病率整体波动于0．5316～3．8317/10万，趋势函数H（t）提示在此期间发病率总体具有缓慢上升的趋势。此外发病率波动的第一隐含周期为19年，但尚未有其他研究支持这一发现；第二隐含周期为5年，这一周期与国内多数猩红热发病规律研究的结论相同或相似［12－14］。值得注意地是自2004年，虽然发病率曲线在趋势上与拟合结果相近，但实际数值却明显较高。对于这一现象，我们提出两种可能的原因：一方面可能是由于猩红热疾病自身特点（如病原体的基因型）与环境因素变化而导致［1，15］；另一方面可能与疾病监测力度有关，由于2003年SARS的爆发，传染病疫情引起了各部门的广泛关注，2004年新的中华人民共和国传染病防治法修订通过并开始执行，同时也开始进行猩红热疫情的网络直报［16］，在这种情况下，对于猩红热监测重视程度也会相应提高，可能会增加对于该疾病的正确识别率与报告率，间接地增高了监测数据中的发病率。

我们首先对于猩红热发病率在时间上进行有序聚类分析，将24年的发病变化在时间上分割为4个阶段，进而获取到各阶段发病率的特点，为提取流行周期提供帮助。有序聚类分析作为一种非监督学习的分类方法，对于各种有序资料（包括时间序列）均可按照其数据结构特征进行最优划分［17］。但同时这种算法目的主要在于将资料合理地分为若干类别以待进一步的分析拟合，故其应用的缺陷是不能直接得出关于序列特征的结论。因此，我们在此基础上，进一步使用周期图法对于猩红热流行周期进行推断，并将聚类分析的结果与隐含周期相结合。目前对于传染病时间序列研究中常用的是较为形象与直观的时域分析，如ARIMA模型，但主要局限性在于容易出现过度差分与过度拟合［18－19］。而周期图法从频域分析的角度通过傅里叶转换的方式提取序列中的隐含周期，并通过若干周期函数的线性相加拟合原始序列，适用于平稳序列的周期提取。应用于非平稳序列时，可通过剔除线性趋势，序列转换等方式首先将原始序列转化为平稳序列。

在有序聚类法划分出的发病率变化的第4个阶段中，按照拟合周期函数的变化趋势，此时处于上升阶段，这一趋势与实际观测值在趋势上基本相同，且按照其周期趋势仍有3～5年的波动上升期。根据其他研究结果显示，2011年前后猩红热在合肥［20］乃至全国其他地区［3，21］均有不同程度的发病升高。因此，我们认为有序样品聚类与周期图法可以较好地用于传染病流行阶段的划分及流行周期的检测。最后，需要注意本次研究中第一隐含周期为19年的结果，也有可能受到诸多因素的影响，如选取序列的长短、地域的不同等，故有待于将来对于更完整的发病率序列进行分析，做进一步验证。

［1］彭晓旻，杨鹏，吴双胜，等．北京地区2011－2014年致儿童猩红热A组链球菌emm基因型别变化特征分析．中华流行病学杂志，2015，36（12）：1397-1400．

［2］Wong SS，Yuen KY．Streptococcus pyogenes and re-emergence of scarlet fever as a public health problem．Emerg M icrobes Infect，2012，1（7）：e2．

［3］You YH，Song YY，Yan XM，et al．Molecular epidem iological characteristics of Streptococcus pyogenes strains involved in an outbreak of scarlet fever in China，2011．Biomed Environ Sci，2013，26（11）：877-885．

［4］Chen YY，Huang CT，Yao SM，et al．Molecular epidemiology of group A streptococcus causing scarlet fever in northern Taiwan，2001-2002．Diagn M icrobiol Infect Dis，2007，58（3）：289-295．

［5］Lima M，Estay SA，Fuentes R，et al．Whooping cough dynam ics in Chile（1932-2010）：disease temporal fluctuations across a north-south gradient．BMC Infect Dis，2015，15（1）：590．

［6］申铜倩，刘文东，胡建利，等．x-11-ARIMA过程在痢疾疫情预测中的应用研究．中国卫生统计，2016，31（3）：395-398．

［7］中华人民共和国卫生部．WS282-2008猩红热诊断标准．北京：人民卫生出版社，2008．

［8］Peng Z，Bao C，Zhao Y，et al．Weighted Markov chains for forecasting and analysis in Incidence of infectious diseases in jiangsu Province，China．JBiomed Res，2010，24（3）：207-214．

［9］（美）Brockwell PJ，Davis RA．著．时间序列的理论与方法（第2版）．田铮译．高等教育出版社，2001：257-266．

［10］乔小妮，李丰森，牛刚，等．基于周期图法的医院门诊流量管理研究．中国数字医学，2015，10（6）：77-79．

［11］陈峰，陆守曾，杨珉．Bootstrap估计及其应用．中国卫生统计，1997，14（5）：5-7．

［12］徐斌，黄夏萍，覃曲波．南宁市1965-2004年猩红热流行特征分析．实用预防医学，2006，13（5）：1208-1210．

［13］马昭君，营亮．2004-2013年连云港市猩红热流行的特征．职业与健康，2015，31（3）：348-350．

［14］周雨．1997-2006年沈阳市和平区猩红热资料分析．预防医学论坛，2009，15（4）：358-359．

［15］Liang Y，Liu X，Chang H，eta1．Epidemiological andmolecular characteristics of clinical isolates of Streptococcus pyogenes collected between 2005 and 2008 from Chinese children．JMed M icrobiol，2012，61（Pt7）：975-983．

［16］李雷雷，蒋希宏，隋霞，等．中国2005-2011年猩红热疫情流行病学分析．中国公共卫生，2012，28（6）：826-827．

［17］杨毅，赵国浩，秦爱民．面板数据的有序聚类分析及其应用-以全球气候变化聚类分析为例．统计与信息论坛，2012，27（7）：13-18．

［18］Zhang T，Yang M，Xiao X，etal．Spectral analysis based on fast Fourier transformation（FFT）of surveillance data：the case of scarlet fever in China．Epidemiol Infect，2014，142（3）：520-529．

［19］Chen B，Sumi A，Toyoda S，etal．Time seriesanalysisof reported cases of hand，foot，and mouth disease from 2010 to 2013 in Wuhan，China．BMC Infect Dis，2015，15（1）：495．

［20］秦薇子，张笑嫣，李萍．2007-2011年度安徽省某三级甲等医院法定传染病疾病谱分析．中华疾病控制杂志，2013，17（3）：251-253．

［21］Lau EH，Nishiura H，Cow ling BJ，et al．Scarlet fever outbreak，Hong Kong，2011．Emerg Infect Dis，2012，18（10）：1700-1702．

（责任编辑：刘 壮）

Application of Sequential Cluster Analysis and Periodogram M ethod in Epidem ic Trend Analysis of Scarlet Fever

Duan Yu，Huang Xiaolei，Wang Yujie，etal
（Departmentof Epidemiology and Biostatistics，School of Public Health，AnhuiMedical University（230032），Hefei）

ObjectiveWe am id to analyze epidem ic trend of scarlet fever in Hefei city and provide predictivemethods for early warning of scarlet fever．MethodsSurveillance data of scarlet fever from 1985 to 2008 were collected from centers for disease control and prevention of Hefei city．Sequential cluster analysiswas used to divide these years into several periods．Periodogram method was used to extract potential cycle and fit the time series of scarlet fever．ResultsThere were altogether 1996 cases of scarlet fever in Hefei city from 1985 to 2008．The average incidence of scarlet fever was 1．9620 per 105．During these years，four clusters were classified by sequential cluster analysis which were 1985－1988，1989－1997，1998－2003，2004－2008，respectively．The first three clusterswere totally 19 yearswhich was equal to the first potential cycle T1 of scarlet fever．In addition，the second potential cycle T2 was equal to 5 in incidence series．ConclusionSequential cluster analysis and periodogram method could be used to extract epidem ic cycles of scarlet fever incidence．

Scarlet fever；Epidem ic cycle；Periodgram method；Sequential cluster analysis

安徽省自然科学基金（编号：1408085MH159）

1．安徽医科大学公共卫生学院流行病与卫生统计学系（230032）

2．安徽省合肥市疾病预防控制中心

△通信作者：王静，E-mail：jwang2006＠126．com