挖掘本质,加深理解
吴汉文●
江苏省平潮高级中学(226361)
挖掘本质,加深理解
吴汉文●
江苏省平潮高级中学(226361)
高中数学的学习节奏相比于初中更快,所以很多学生步入高中后难以适应,造成对知识点和例题的学习仅仅局限于表面,难以深入的体会、理解、掌握,这样随着知识难度的加大,学生懂得越来越少,学习动力也会越来越小,从而导致消极对待数学学习.因此,老师要帮助学生深入理解课本内容,让学生头脑清晰地学习数学,对知识的掌握更加牢固,本文从挖掘本质方面进行说明.
高中数学;挖掘本质;探究;理解
一、挖掘定理公式本质
定理公式是课本上最基本的知识点,是学生进行后续学习的基础,只有把基本定理理解透彻,才会在进一步的深入学习中不落下风.揭示定理公式的本质即换一种学生易理解的方式进行描述,让学生可以很快掌握定理本质,灵活运用.
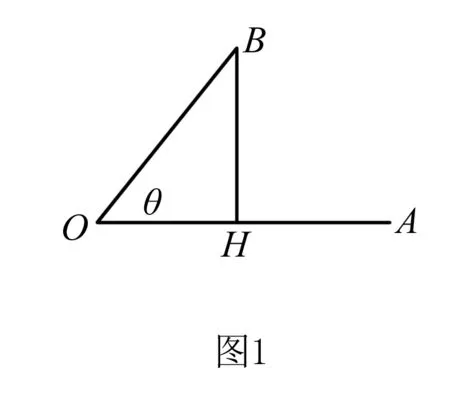
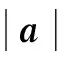
学生1:在一个向量上作另一个向量的投影,但是这两个向量要有一个共同的起始点.
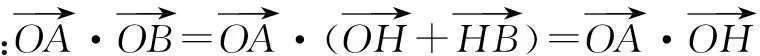
学生2:把本来不共线的两个向量转化为两个共线的向量和两个相互垂直的向量.通过这种转化,把问题简单化,从而得出任意两个向量数量积的公式.
师:对,通过上述的推导,我们可以直接得出向量数量积的几何意义.
在挖掘课本定理本质过程中,教师往往会用到一些辅助方法,通过这些方法不仅可以让学生理解定理本质,更是开阔了学生思维,教会了学生解题思路,因此挖掘本质可谓一举两得.
二、挖掘解题思路本质
同一个问题,不同的人会用不同的角度看待,其思考解决的问题也就有所不同,但是在这些复杂多样的思维之下一定会有一个共性,考察的知识点是不变的.如果可以让学生通过解题策略的本质探究,让学生的思维找到知识的源头,那么学生的思维就会在这个过程中得到提炼和升华,课堂内容精致简练也会极大提升学生的学习热情,促进让学生对题目的本质理解.
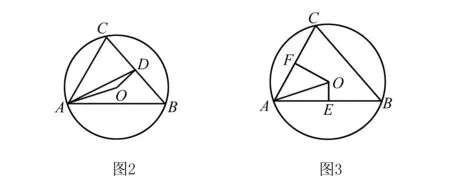
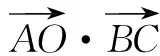
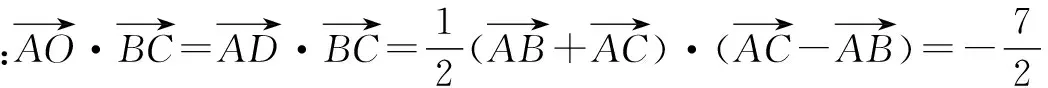
老师:还有其他解法吗?
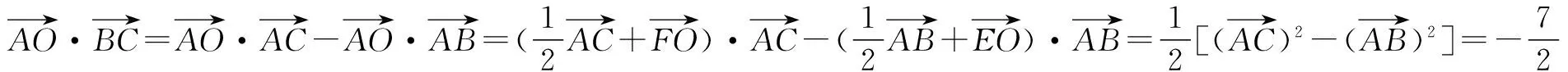
老师:做得非常好!这两种方法都是把不共线的两向量转化成为两个共线的向量,而且方法中都用了作垂线的方法,知识运用得很灵活.
可以看出,相同的题目思考的起点都是相同的,只是获得结果的过程不同,通过对不同解法的探究挖掘,帮助学生对一个知识的本质有了清晰的认识,对同一类型题目的考察知识有了更深刻的理解.
三、挖掘题目条件本质
在解题过程中我们要懂得回归题目,从题目条件出发反思解题方法,在挖掘题目时要思考是否能把条件弱化或者泛化,我们要让学生养成挖掘题目信息的习惯,让学生在题目条件中与自己学习的知识结合起来,让学生去思考题目中的信息与学生学习的哪方面知识可以联系起来,这样在解题过程中也能加深学生对知识的理解.
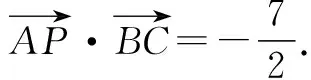
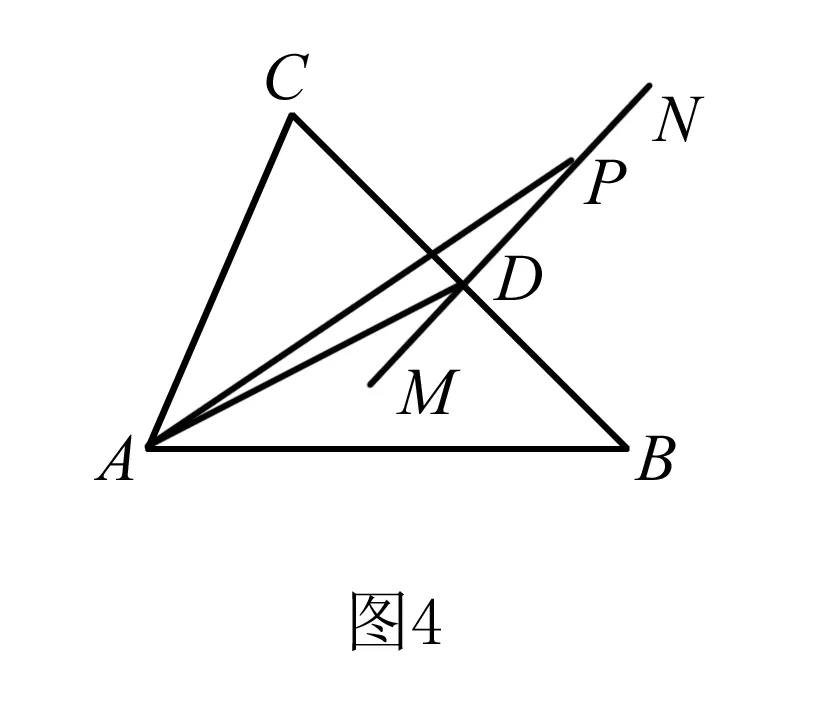
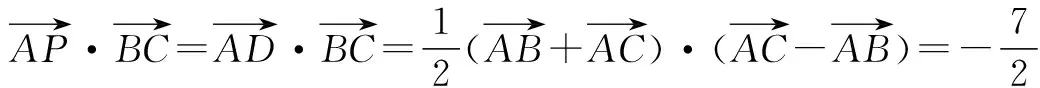
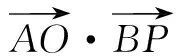
高中数学知识理解最为重要,理解知识要从题目出发,挖掘题目中不同方面的本质可以有助于学生加深知识的理解,学生理解知识后会进一步增强自己可以掌握数学的信念,这正是我们所要的学习自信.
G632
B
1008-0333(2016)34-0037-01

