高中数学极限问题解题的常用方法

曹 军●

江苏省丰县中学(221700)

高中数学极限问题解题的常用方法

曹 军●

江苏省丰县中学(221700)

高中数学知识内容较多较复杂.其中极限问题是高中教学中的难点，极限思想在多种数学问题中都有应用，因此熟练掌握高中数学极限问题的解法非常重要.

一、数列中的极限问题

数列是高中数学教学中的重要内容，其中很多题目需要借助极限思想来进行解决.数列的解题过程用一般方法都比较复杂，并且解题过程很难理解，但通过极限思想的应用，能够简化解题过程，促进学生更轻松的理解和解答.数列的学习中，需要学生首先掌握等差数列的定义、通项公式、前n项和的公式等，然后教师需要让学生接触更多关于等差数列的各种变形的题目，从而接触数列中更加深入的内容.如题1，已知{an}是一个等差数列，首项a1=31，公差d=-8，求此数列的前n项和的最大值，并确定n的值.针对这种类型的题目，在解答时首先应清楚题目中给出的公差是负数，因此在求解的过程中如果是求前n项和的最大值，首先应找到变成负数的项，由此可以找出n的值.这个题目的求n的过程中，n就是一个极值，通过教材学习可以得知等差数列的通项公式是an=a1+(n-1)d，通过计算可知，a4=7，a5=-1，这样可以得知当n=4时，Sn此时为最大值.极值在数列中的应用能够巧妙化解数列问题的难点，使得复杂的数列变得更加简单，也让学生能够掌握更加简便的解题方法.

二、函数中的极限问题

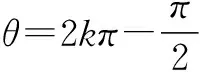
三、几何中的极限问题

几何部分中也有很多涉及极限思想的问题，通过巧用极限简化解题步骤，教师在进行几何的教学中，尤其是在讲解一些求面积、体积等的问题中，可以引导学生通过极限思想进行思考，让学生学会解决几何中的极限问题.如几何中常用的三角形三边之间的和差关系，两点之间线段最短的原则，定点和定直线之间垂线段最短等知识点，这些知识点延伸的几何问题都可以转化成极限问题，通过极限思想来解决.

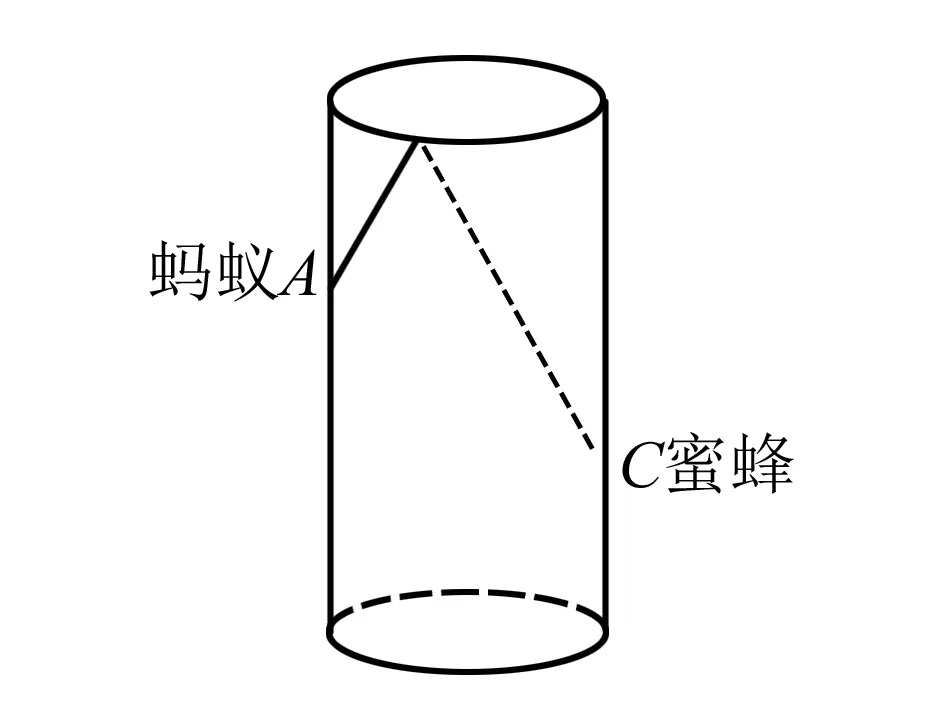
如题3，现有一个圆柱形的圆桶如图1，已知圆桶的底面的周长是15厘米，高是10厘米，在桶内壁距离桶底4厘米的点C处有一滴蜂蜜.而在距离桶上沿4厘米的点A处有一个蜜蜂，问蜜蜂到达蜂蜜处最短距离是多少？通过分析这个问题可知，这个题目考查的知识点是两点之间的最近距离.通过将桶的侧面展开，这个问题就可以转化成平面几何问题，从而转化成求极值的问题，简化了问题解决的过程.对于这种类型的题目，需要对题干进行分析，将其简化成单纯的数学问题，将几何图形的问题简化成能够通过数字运算简便解决的题目，从而提高学生解题的效率.又如题4，求正三棱锥两侧面所形成的二面角的范围.常规解题方法是首先构造一个二面角的平面角，然后引入很多变量来求三角函数值的范围，通过三角函数的性质来解决，这种解题过程比较复杂，并且涉及很多内容，学生在解题时容易出错，又不好理解.但通过记正三棱锥为A-BCD，然后令A趋向无限远，来观察分析三棱柱两侧面ABC与ABD所成的角，分析其范围，从而得出结果.

四、不等式中的极限问题

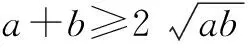
总之，极限思维在高中数学中的应用比较广泛，教师在教学中应培养学生的极限思维，让学生能够熟练掌握高中数学极限问题的解决方法，增加学生学习的主动性，让学生能够更加轻松愉快地学习.

G632

B

1008-0333(2016)34-0027-01