概率与函数交汇题型赏析
张同语●
安徽省五河县第一中学(233300)
概率与函数交汇题型赏析
张同语●
安徽省五河县第一中学(233300)
概率是新课程高考的一大热点,而函数又是高中数学的主线,将概率与函数进行融合,使它们交汇联袂,能多角度考查学生的探究能力和创新意识,给人以耳目一新的感觉.本文以全国各地的高考模拟试题为例,以示说明.
一、选填题——二者交汇有魅力
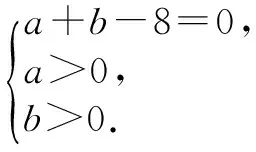
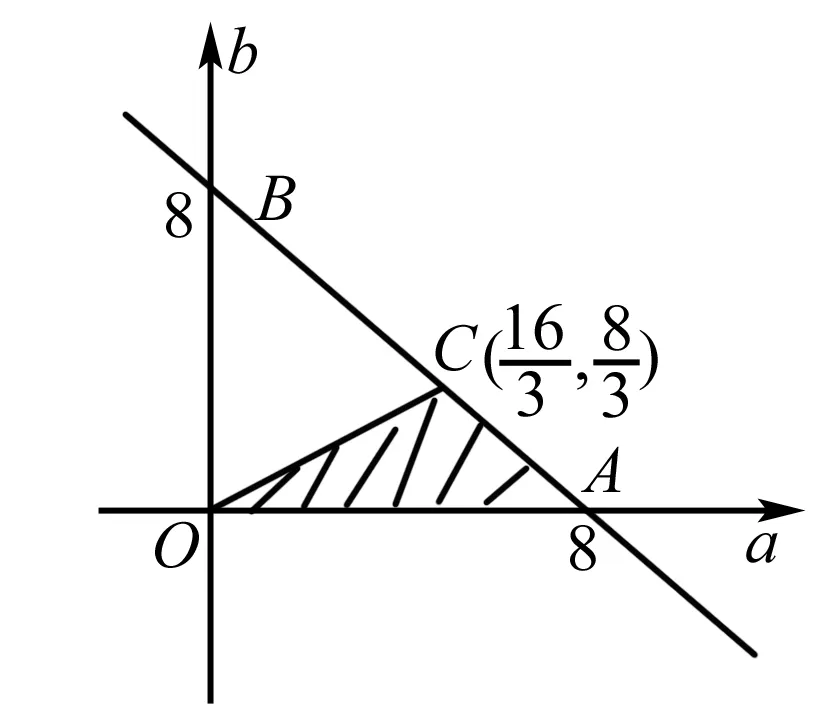
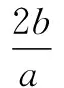
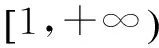
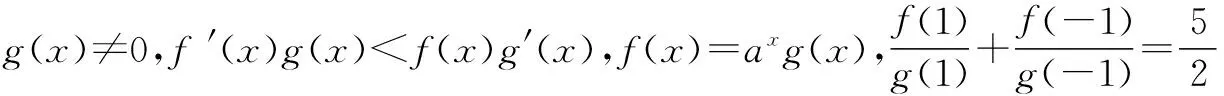
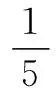

赏析 本题将函数、导数、数列、概率等交汇在一起考查,充分体现了高考在知识交汇点处设计试题的命题指导思想,体现了“小、巧、精、活”的特点,是一道难得的好题,要求考生能运用所学知识解决学科内的小型综合题.
二、解答题——二者交汇有活力
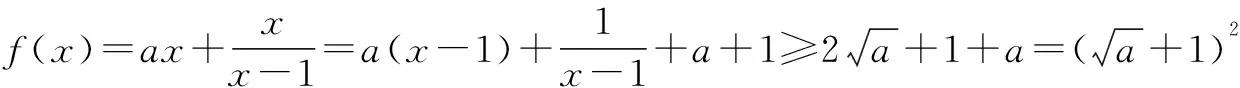
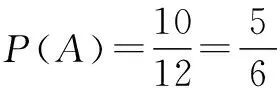
赏析 本题将函数、不等式恒成立、概率等有机结合进行考查,给人以耳目一新的感觉,独具匠心.
例4 一个盒子里装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
①现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得新函数是奇函数的概率;
②现从盒子中逐一抽取卡片,且每次取出后均不放回,若取得一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
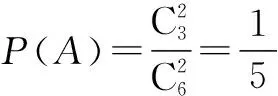
②ξ可取1,2,3,4.

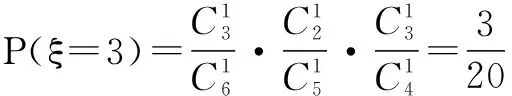
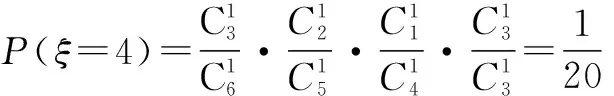
∴ξ的分布列为

ξ1234P12310320120
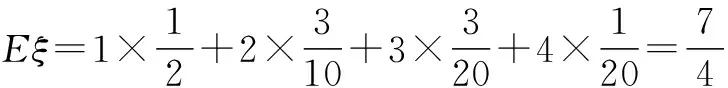
赏析 本题将函数的奇偶性、概率、随机变量的分布列和数学期望等一并考查,衔接自然,叙述流畅,情景新颖,具有较好的选拔区分功能.
例5 四个大小相同的小球,分别标有数字1,1,2,2,把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为x,y,记ξ=x+y.
①求随机变量ξ的分布列和数学期望;
②设“函数f(x)=x2-ξx-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率.

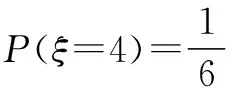

ξ1234P12310320120
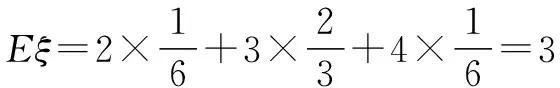
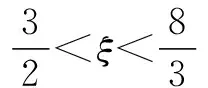
赏析 本题将四个小球进行合理编号是正确求出随机变量的分布列的数学期望的基础,第②问将函数的零点融入其中考查,体现了新课标理念的渗透.
G632
B
1008-0333(2016)34-0010-02

