速冻水饺金黄色葡萄球菌定性检验测量不确定度评估

速冻水饺金黄色葡萄球菌定性检验测量不确定度评估

陆俊波 安庆市食品药品检验中心

为减小实验误差，提高检测结果精确度，评定金黄色葡萄球菌计数的不确定度。分析速冻制品（水饺）中金黄色葡萄球菌计数不确定度的来源，采用合并样本标准差的方法来评定金黄色葡萄球菌计数的不确定度。测量结果表明，扩展不确定度为0.08%，该方法简便，适合于每一个样本的检验结果，随着检验结果的不断增加，可随时加入到合并样本中，重新计算合并样本标准差，更新其不确定度的取值范围。

目的

评价金黄色葡萄球菌定性检验测量不确定度评估。

评定方法

依据《测量不确定度评定方法与表示》（JJF1059-1999）和《食品微生物学检验 金黄色葡萄球菌检验》（GB 4789.10-2010），参照国际通行的菌落数检测结果的不确定度评定方法。

检验方法

依据GB4789.10-2010食品卫生检验方法微生物学部分，以无菌操作取检样25 g放于含有225 mL灭菌生理盐水的无菌均质杯中，8 000～10 000 r/min均质1～2 min制作成1∶10的均匀稀释样液。根据食品卫生标准或对污染情况的估计，选择2～3个稀释度，再进行10倍递增稀释，每个稀释度分别吸取1 mL样品匀液以0.3、0.3、0.4 mL接种量分别加入3块Baird-parker平板，然后用无菌L棒涂布整个平板，涂布后静置10 min，如样液不易吸收，可将平板放在培养箱（36±1）℃培养1 h；等样液吸收后翻转平板，置（36±1）℃培养箱内培养45～48 h。

达到培养时间后，根据平板计数的情况选择公式（1）或公式（2）进行典型菌落的计数。

公式（1）：

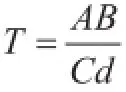
其中，T为样品中金黄色葡萄球菌菌落数；A为某一稀释度典型菌落的总数；B为某一稀释度血浆凝固酶阳性的菌落数；C为某一稀释度用于血浆凝固酶试验的菌落数；d为稀释因子。

公式（2）：

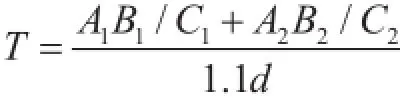
其中，T为样品中金黄色葡萄球菌菌落数；A1为第一稀释度（低稀释度）典型菌落的总数；A2为第二稀释度（高稀释度）典型菌落的总数；B1为第一稀释度（低稀释度）血浆凝固酶阳性菌落数；B2为第二稀释度（高稀释度）血浆凝固酶阳性菌落数；C1为第一稀释度（低稀释度）用于血浆凝固酶试验的菌落数；C2为第二稀释度（高稀释度）用于血浆凝固酶试验的菌落数；d为稀释因子。

不确定度来源

在微生物检验中，样品中细菌分布的均匀性和重复测量带来的不确定度是影响检验结果准确度的主要原因，而B类不确定度分量对合成不确定度影响较少。按《食品微生物学检验》（GB 4789.10-2010）中的方法，同一样品每个稀释度分别吸取1 mL样品匀液以0.3、0.3、0.4 mL接种量分别加入3块Baird-parker平板，因此可以采用合并样本标准差求检测结果的不确定度。适合A类的评估方式。

数学模型

准备同一食品（水饺）16份样品，通过对16份样品加入目的菌的检测，估算每一份样品的微生物含量。

各样品分别由不同人员进行测量，同一样品的两次测量由同一人员进行，X1和X2为两次测量结果，X为两次测量平均结果。

设菌落总数为A，检测结果为X，则A=x cfu/g。

不确定度的计算

（1）列出每一样品的两次测量结果X1和X2，见表1。

从检验结果可知，如直接用贝塞尔公式计算合并样本标准差，由于数据的散发性较大，计算出的合并样本标准差很大，当样本均值较小时其不确定度则会过大，此时可以对上述数据取对数后，计算出样本检验结果对数值的均值和残差，将中间计算结果，见表2。根据贝赛尔公式，可计算出检测结果对数值的合并样本标准差：对测量结果取对数，得到每一样品的logX1和logX2两次测量的平均值。

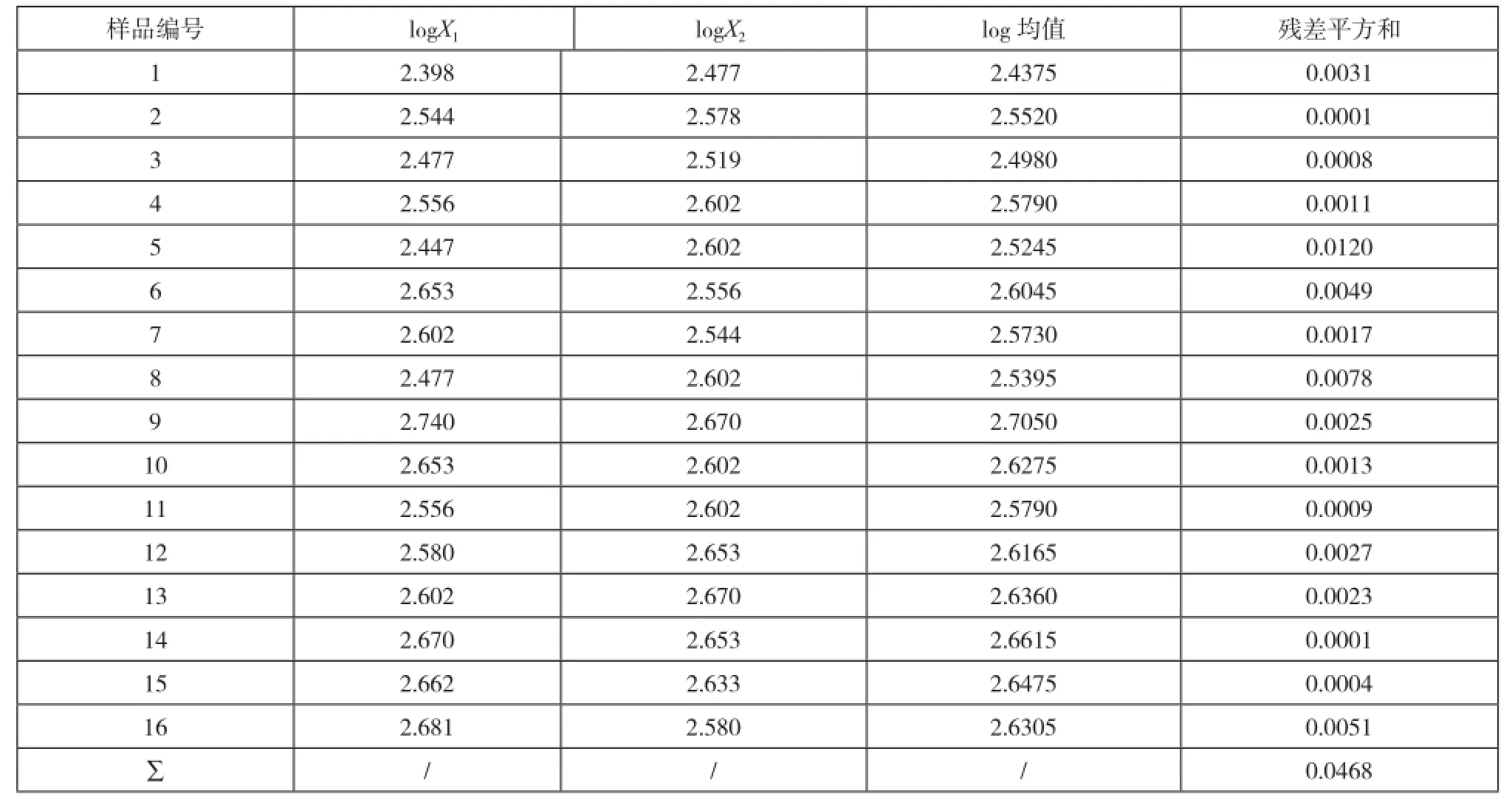
表2 16份样品分别求残差平方和

表1 16份样品两次检测结果

（2）由各样品的残差平方和，计算其合并样本平方差，得到：

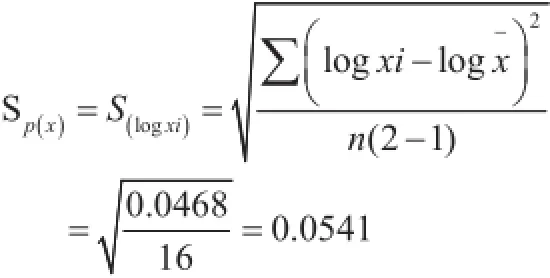
（2）合成标准不确定度

每一样品测量两次，因此两次测量平均值的试验标准差即合成标准不确定度为：

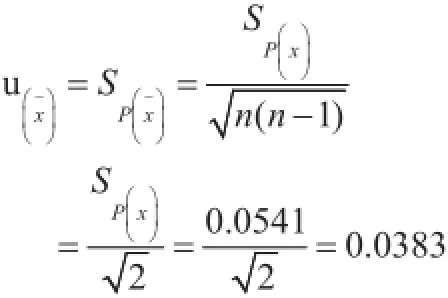
（3）扩展不确定度

取包含因子k=2，得：

（4）金黄色葡萄球菌数测量平均值：395.9375≈396。

结果报告

水饺中金黄色葡萄球菌平均计数A=396 cfu/g，扩展不确定度U(A)为32 cfu/g，K=2。

应用

以第1个样品为例，两组结果250和300的log值的平均值为2.437 5，因此取值区间为2.437 5±0.08，即分布于2.5175～2.3575，取反对数的平均值的取值区间为300～250。

以第2个样品为例，两组结果350和380 的 log值的平均值为2.552 0，因此取值区间为2.552 0±0.08，即分布于2.6320～2.4720，取反对数的平均值的取值区间为350～380。

以第3个样品为例，两组结果300和330 的log值的平均值为2.498 0，因此取值区间为2.498 0±0.08，即分布于2.5780～2.4180，取反对数的平均值的取值区间为300～330。

以第16个样品为例，两组结果480和380的log值的平均值为2.630 5，因此取值区间为2.630 5±0.08，即分布于2.710 5～2.550 5，取反对数的平均值的取值区间为480～380。

结论

从计算结果可知，由于检验结果的散发性较大，如直接用贝赛尔公式计算合并样本标准差所得到的不确定度不适合每一个样本。当检验结果取对数后，用合并样本标准差求检验结果的不确定度则使用方便，且适合于每一个样本。随着检验结果的不断增加，可随时加入到合并样本中，重新计算合并样本标准差，更新其不确定度的取值范围。