基于随机矩阵理论和最小描述长度的机载前视阵雷达杂波自由度估计
李 海 刘新龙 蒋 婷 吴仁彪
基于随机矩阵理论和最小描述长度的机载前视阵雷达杂波自由度估计
李 海*刘新龙 蒋 婷 吴仁彪
(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)
有限训练样本时,总体协方差矩阵特征谱的严重扩展使得机载前视阵雷达杂波自由度估计困难。该文提出一种前视阵杂波自由度估计方法,该方法利用随机矩阵理论(Random Matrix Theory, RMT)中特征值统计分布特性建立参数化的概率模型,结合最小描述长度(Minimum Description Length, MDL)准则关于信源检测的思想估计杂波自由度。该方法能够在有限训练样下实现杂波自由度的有效估计,仿真结果验证了方法的有效性。
前视阵雷达;杂波自由度;随机矩阵理论;最小描述长度;协方差矩阵
1 引言
空时自适应信号处理(Space-Time Adaptive Processing, STAP)[1,2]是现代预警雷达的核心技术,其联合空时域进行杂波抑制,是进行有效动目标检测的前提。杂波自由度(即杂波协方差矩阵大特征值个数)是反映杂波特征的重要参数,是设计STAP降维算法以及确定训练样本数的理论依据[3]。国内外学者针对杂波自由度进行了广泛的研究,其中Brennan准则[1,4]是杂波自由度估计的主要依据,但该准则仅适用于理想的机载正侧视阵雷达系统;对于机载前视阵雷达系统尚没有确切的理论估计准则。
实际应用中,可通过估计杂波协方差矩阵的特征谱进行杂波自由度估计;其中,基于主分量分析(PCA)的低秩逼近方法[5]是典型的估计方法。但机载雷达所面临的实际环境比较复杂,杂波往往具有非均匀特性[3]。尤其在机载前视阵雷达中,杂波具有距离依赖性[6],因此,很难获得足够多独立同分布(Independent and Identically Distributed, IID)的训练样本。当训练样本数不足时,特征谱存在严重扩展,即特征谱中无明显的拐点,使得该类方法估计杂波自由度变得困难。
近年来,随机矩阵理论[7,8](Random Matrix Theory, RMT)得到了国内外学者的广泛关注,该理论研究随机矩阵的经验谱分布特性,现已被广泛用于研究MIMO系统[9]、非参数化信源检测[10]、子空间估计[11]、频谱感知[12]等领域。本文结合信息理论准则[13]的信源检测思想,利用RMT中估计协方差矩阵特征值的统计分布特性建立参数化的概率模型,通过最小描述长度(Minimum Description Length, MDL)准则[14,15]估计杂波自由度。最后,将所提方法与特征对消空时自适应处理(Eigen- Canceler Space-Time Adaptive Processing, EC-STAP)[16]相结合进了仿真实验,仿真结果验证了方法的有效性。
2 数据模型及随机矩阵理论
2.1 数据模型
机载前视阵雷达几何模型如图1所示,这里以均匀线阵为例。其中,为载机高度,表示载机速度;是斜距为上的杂波散射点,其方位角为,俯仰角为。

图1 机载前视阵雷达几何模型

(2)

(4)

(6)

(8)

2.2 随机矩阵理论


图2 Marčenko-Pastur概率密度示意图
3 杂波自由度估计
杂波自由度可由总体协方差矩阵大特征值个数估计,该大特征值定义为大于热噪声功率的特征值。然而当样本数有限时,由Marčenko-Pastur律可知,估计协方差矩阵特征谱存在严重扩展;即噪声对应的特征值围绕噪声功率存在起伏,部分将大于噪声功率而被认为是大特征值,导致杂波自由度估计不准确。
由第2节可知,杂波数据是由多个散射体回波的叠加,即可将其建模为一种分布式干扰源[1],而杂波自由度表征了其干扰源的个数。由于训练样本的回波数据除杂波外还包括热噪声,故杂波自由度的估计相当于是热噪声背景中的信源检测。文中以RMT中估计协方差矩阵特征值的统计分布特性建立参数化的概率模型,结合信源检测的思想,利用MDL准则[14,15]估计杂波自由度。以下分别从构造检验统计量和代价函数两个方面对本文方法进行讨论。
3.1 构造检验统计量

(13)
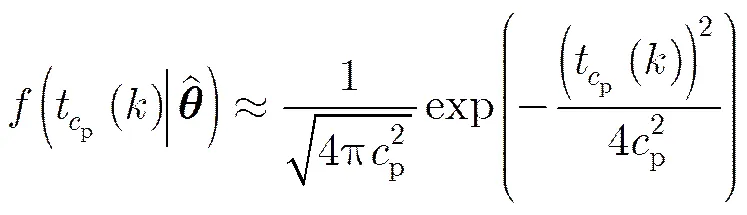
(15)
3.2 构造代价函数
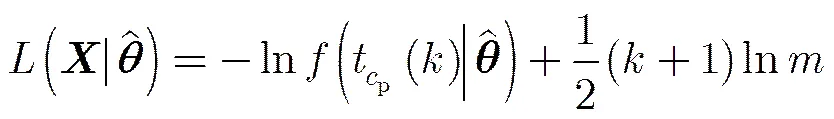
(17)

4 仿真实验
本节将所提方法与特征对消空时自适应处理(EC-STAP)[16]相结合进行了仿真实验,分别从杂波自由度估计、改善因子(IF)[1]以及收敛速度3个方面进行验证。机载前视阵杂波数据按照Ward模型[20]产生,具体仿真参数如表1所示,以下仿真中,分别在不同系统维数时进行验证,故表1中没有给出具体的系统维数。

表1 仿真参数

(20)
4.1 杂波自由度估计

图3 n=256时杂波自由度估计
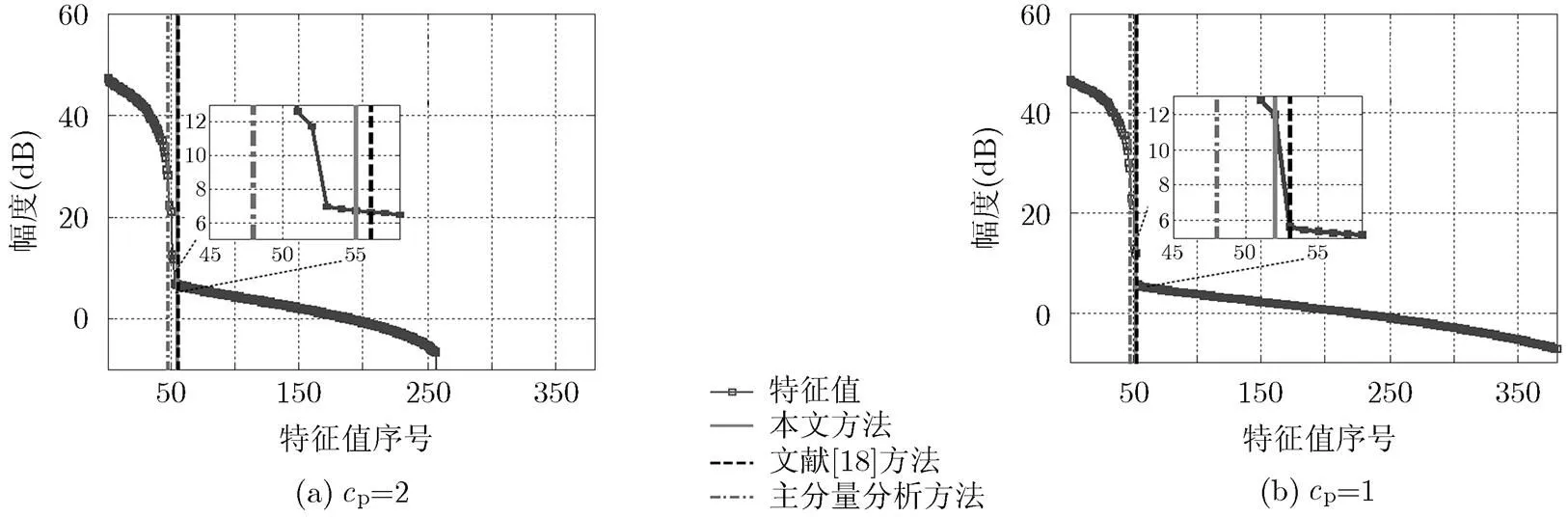
图4 n=512时杂波自由度估计
4.2 IF比较
4.3 收敛速度比较
5 结束语
本文针对有限训练样本数时机载前视阵雷达杂波自由度估计,提出一种新的杂波自由度估计方法。该方法将杂波自由度估计等价于热噪声中的信源检测问题,利用随机矩阵理论中估计协方差矩阵特征值的统计分布特性,通过最小描述长度准则估计杂波自由度。该方法是一种信息论准则的估计方法,相比于传统主分量分析方法,具有无需确定低秩逼近系数和收敛速度快的特点;该方法为有限训练样本数时杂波自由度估计提供了一种新思路。

图5 n=128时改善因子比较 图6 n=128时收敛速度比较
参考文献
[1] GUERCI J R. Space-Time Adaptive Processing for Radar [M]. Norwood, Artech House, 2014: 1-74.
[2] FERTIG L B. Analytical expressions for Space-Time Adaptive Processing (STAP) performance[J]., 2015, 51(1): 42-53. doi: 10.1109/TAES.2014.130676.
[3] DEGURSE J F, SAVY L, and MARCOS S. Reduced-rank STAP for target detection in heterogeneous environments[J]., 2014, 50(2): 1153-1162. doi: 10.1109/TAES.2014.120414.
[4] BRENNAN L E and STAUDAHER F M. Subclutter visibility demonstration[R]. Technical Report RL-TR-92-21, Adaptive Sensors Incorporated, 1992.
[5] SHLENS J. A tutorial on principal component analysis[OL]. http://arxiv.org/abs/1404. 1100, 2014.
[6] 同压龙, 王彤, 文才, 等. 一种稳健的机载非正侧视阵雷达杂波抑制方法[J]. 电子与信息学报, 2015, 37(5): 1044-1050.doi: 10.11999/JEIT141222.
TONG Yalong, WANG Tong, WEN Cai,. A robust clutter suppression method for airborne non-sidelooking radar[J].&, 2015, 37(5): 1044-1050. doi: 10.11999/JEIT141222.
[7] BAI Z D and SILVERSTEIN J W. Spectral Analysis of Large Dimensional Random matrices[M]. New York: Springer, 2010: 1-13.
[8] Random matrices and their applications[OL]. http://djalil. chafai.net/wiki/hk2015:start.2015.
[9] ZWINGELSTEIN C M and DEBBAH M. Random matrix theory based resource allocation in correlated MIMO systems with ARQ feedback[J]., 2014, 18(5): 793-796. doi: 10.1109/LCOMM.2014.031414.140214.
[10] KRITCHMAN S and NADLER B. Non-parametric detection of the number of signals: hypothesis testing and random matrix theory[J]., 2009, 57(10): 3930-3941. doi: 10.1109/TSP.2009.2022897.
[11] VALLET P, LOUBATON P, and MESTRE X. Improved subspace estimation for multivariate observations of high dimension: the deterministic signals case[J]., 2012, 58(2): 1043-1068.
[12] AHMED A, HU Y F, NORAS J M,. Random matrix theory based spectrum sensing for cognitive radio networks [C]. Internet Technologies and Applications, Wrexham, 2015: 479-483.
[13] WAX M and KAILATH T. Detection of signals by information theoretic criteria[J].Acoustics,,, 1985, 33(2): 387-392. doi: 10.1109/TASSP.1985.1164557.
[14] BARRON A, RISSANEN J, and YU B. The minimum description length principle in coding and modeling[J]., 1998, 44(6): 2743-2760. doi: 10.1109/18.720554.
[15] HUANG L and SO H C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J]., 2013, 61(19): 4806-4821. doi: 10.1109/TSP.2013. 2273198.
[16] HAIMOVICH A M and AYOUB T F. The eigencanceler: Space time adaptive radar by eigenanalysis methods[R]. New Jersey Inst of Tech Newark, 1999.
[17] MARčENKO V A and PASTUR L A. Distribution of eigenvalues for some sets of random matrices[J].:, 1967, 1(4): 457-483.
[18] NADAKUDITI R R and EDELMAN A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples[J]., 2008, 56(7): 2625-2638. doi: 10.1109/TSP.2008. 917356.
[19] BAI Z D and SILVERSTEIN J W. CLT for linear spectral statistics of large-dimensional sample covariance matrices[J]., 2004, 32(1): 553-605.
[20] WARD J. Space-time adaptive processing for airborne radar [R]. Technical Report 1015, MIT Lincoln Laboratory, 1994.
[21] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]., 1974, 10(4): 853-863. doi: 10.1109/TAES.1974.307893.
李 海: 男,1976年生,副教授,研究方向为空时自适应信号处理、机载气象雷达信号处理等.
刘新龙: 男,1984年生,硕士生,研究方向为空时自适应信号处理、动目标检测.
蒋 婷: 女,1990年生,硕士生,研究方向为机载气象雷达信号处理.
吴仁彪: 男,1966年生,教授,研究方向为自适应阵列信号处理及其应用.
Estimation of Clutter Degrees of Freedom in Airborne Forward-looking Radar via Random Matrix Theory and Minimum Description Length Criteria
LI Hai LIU Xinlong JIANG Ting WU Renbiao
(,,300300,)
Owing to the heavy spread of eigenspectrum of the population covariance matrix under finite training samples condition, it is a challenge to estimate the clutter Degrees of Freedom (DoF) in airborne forward-looking radar. In this work, a method for estimation the clutter’s DoF is proposed. In order to estimate the clutter’s DoF, an idea from sources detection by Minimum Description Length (MDL) criterion is borrowed, and the parametric probability model is formed based on the eigenvalue’s statistical distribution properties from Random Matrix Theory (RMT). The proposed method is effective to estimate the clutter’s DoF under finite training samples condition, and the simulation results verify the efficiency of the proposed method.
Forward-looking radar; Clutter Degrees of Freedom (CoF); Random Matrix Theory (RMT); Minimum Description Length (MDL); Covariance matrix
TN958
A
1009-5896(2016)12-3224-06
10.11999/JEIT160132
2016-01-29;改回日期:2016-06-23;
2016-09-08
李海 haili@cauc.edu.cn
国家自然科学基金(61471365, 61571442, 61231017); 中央高校基本科研业务费项目(3122015B002),中国民航大学蓝天青年学者培养经费
The National Natural Science Foundation of China (61471365, 61571442, 61231017), The National University’s Basic Research Foundation of China (3122015B002), The Foundation for Sky Young Scholars of Civil Aviation University of China
——以鲁甸地震相关新浪微博为例

