不同时间频次的外强迫对全球大洋海温模拟的影响

史珍，李响，刘娜

不同时间频次的外强迫对全球大洋海温模拟的影响

史珍，李响，刘娜

（国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室，北京100081）

研究了不同时间频次外强迫对全球海洋环流模式MOM4的海温模拟的影响，并分析了其影响海温模拟的物理机制。结果表明：由于时间平均产生的不同时间频次的外强迫具有相同的气候态，但是其强度差异较大。采用不同时间频次的外强迫均能较好的重现全球海温的大尺度时空分布特征，且对海温异常的模拟跟观测较为接近，但是不同时间频次外强迫对全球海温平均值的模拟偏差较大，其中逐6 h的外强迫模拟的全球平均海温相对于逐月外强迫模拟的全球平均海温改进了0.74℃。高频强迫模拟的海温更加接近观测，其对全球海洋起着冷却的作用。这种冷却作用在中高纬度海域主要通过加强垂直混合导致，而在低纬海域可能是平流过程及热通量导致。

MOM4；时间频次；外强迫；海温

1 引言

早期由于缺乏海上风场与热力场的观测，海洋模式通常采用相对低时空分辨率的外强迫数据。基于小尺度高频外强迫对大尺度低频海洋的气候变率不存在显著影响的假定，小尺度海洋模式进行短时模拟的研究中偶尔采用由浮标观测得到的高时空分辨率的动力及热力场[1]，大尺度海洋气候模式则通常都采用低分辨率的外强迫数据。但是该假定并不是普遍适用的，Large等[2]利用高频风场强迫一个北太平洋的准地转模式的结果表明：高频风场外强迫对海洋的斜压过程及深层动能有一定的影响。Chen等[3]利用一个“人造”的高频风场强迫模式，发现高频风场外强迫可以通过垂直混合显著的降低海表温度（Sea Surface Temperature，SST）。随着海洋观测的进步，出现了越来越多高时间分辨率的数据，许多研究开始关注高时间分辨率的外强迫数据对海洋模拟的影响。Chen等[4]利用NASA Scatterometer(NSCAT)的观测风场，研究了高时空分辨率风场外强迫对1997—1998年El Niño爆发的影响，发现时间平滑后的风场通过减少垂直湍流混合的能量而加热SST，而空间平滑的风场则没有时间平滑的风场那么明显的加热SST，但是对海洋动力过程的响应具有重要的影响。Sui等[5]研究了逐日的表面强迫场对赤道太平洋上层海洋的影响，结果表明高频的表面强迫场对SST具有冷却作用，其主要通过加强垂直混合来减少上层海洋的垂直层结，同时减少进入海洋的净热通量及经向热平流这两个机制实现。Kara等[6]研究了不同时空分辨率的数据强迫HYCOM（Hybrid Coordinate Ocean Model）模式对黑海海温及海流模拟的影响，结果表明高频的大气强迫场对黑海沿岸流的加强及中尺度涡的形成具有非常显著的影响。Casella等[7]对利古里亚海的研究得到了跟Kara等人的研究类似的结论。Cardona等[8]用ROMS（Regional Ocean Modeling System）模式研究了高频风场对南海海洋模拟的影响，结果表明高频风场对水平环流的模拟没有显著影响，但对垂直速度场有较大的影响，主要机制是惯性频率附近以及更高频的风场会激发涡旋Rossby波及惯性波，而这些波动控制了混合层以及100 m以上层的垂直速度场。除了研究不同时间分辨率的外强迫对区域海洋模式模拟的影响，科研人员也研究了不同时间分辨率高频风场对全球海洋模拟的影响。Lee等[9]的研究通过采样方式得到的不同时间分辨率的外强迫场，其结果表明高频风场数据对减小模式误差具有非常重要的作用，主要机制是通过采样的方式一方面减少了风场的高频分量，减弱垂直混合而影响中高纬海域的混合层深度及海表温度；另一方面改变风场的年平均值，进而导致平流的差异而影响低纬海域及沿岸海域。

目前，国内关于这方面的研究开展的相对较少，但是该研究对建立海洋气候预报系统非常重要，因此非常有必要进行该方面的研究探索。同时，国际上对不同时间分辨率的外强迫对海洋模拟的影响机制并未形成一致的结论，这也需要进一步的进行研究。另外，以往的研究中并未采用过气候预测系统的大气再分析数据CFSR（Climate Forecast System Reanalysis）作为强迫数据，那么这种数据的差异是否对研究不同频次大气外强迫对海洋模拟产生不同的影响？这也是亟需回答的问题。因此，本文针对以上问题，开展了不同时间分辨率的CFSR外强迫数据对全球海温模拟影响的研究。

2 模式、试验及数据介绍

2.1 模式介绍

研究中所用海洋环流模式为MOM4（The Module Ocean Model Version 4）[10]。该模式是由美国地球流体力学实验室（The Geophysical Fluid Dynamics Laboratory，GFDL）开发的模块化海洋模式，为自由表面原始方程海洋模式，采用非Boussinesq近似和静力近似。模式的水平网格为Arakawa B网格，垂直坐标为z坐标系。模式提供了多种垂直混合参数化方案，包括KPP方案、Richardson数决定的涡动混合系数法等。

该研究中，模式的计算范围包含了全球所有大洋，水平网格分辨率为1/4°×1/4°，垂直方向分为50层，其中海表浅层加密垂向层数，最大水深取为5 500 m。模式中海底地形数据采用OCCAM的0.2°资料。模式采取三极点网格，可以有效消除全球模式在北极的奇点。模式中温、盐、流速及自由表面的积分步长均取为1 500 s,流函数的积分时间步长取为25 s。首先，利用美国国家大气研究中心的海洋模式比较计划（OMIP_NCAR）气候态数据强迫MOM4模式，从静止海洋状态积分20 a，使海洋模式运行到一个稳定的状态。在此基础上，以气候态运行的最后一个时刻的物理量场作为高频强迫试验的初始场，采用CFSR实时数据强迫MOM4模式积分28a，大气强迫数据分别采用不同时间频次（6 h、逐日、月平均）的CFSR数据集。所有外强迫资料均经过插值以适应模式需要。

2.2 试验设计与数据介绍

为了考察不同时间分辨率的外强迫对MOM4模式的海温模拟结果的影响，本文设计了3组试验，分别为：采用CFSR的逐6 h数据集作为外强迫的试验，记为CFSR_6h；采用CFSR的逐日数据集作为外强迫的试验，记为CFSR_Day；以及采用CFSR的月平均数据集作为外强迫的试验，记为CFSR_Mon。

需要特别指出的是，逐日的CFSR数据及月平均的CFSR数据均由时间分辨率为逐6 h数据集通过计算日平均值与月平均值获得，这保证了这几套外强迫数据的气候态是相同的。

本文研究中用到的主要数据包括：

（1）美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）的CFSR数据[11]。研究中该数据的时间范围为1981年1月—2008年12月，时间分辨率为逐6 h，水平分辨率为0.5°。该数据作为CFSR试验的外强迫数据驱动MOM4模式；

（2）美国马里兰大学的海洋再分析数据（Simple Ocean Data Assimilation，SODA）[12]，该数据为月平均数据，时间范围为1981年1月—2008年12月，水平分辨率为0.5°，垂直共40层。该数据作为海洋的观测数据与3组试验数据进行对比。

3 结果分析

3.1 全球平均海表温度

海洋模式的评估中，SST为第一考核指标。图1给出了SODA以及3组试验模拟的全球月平均SST随时间的变化。从图中可以看出，3组试验的平均SST与SODA的平均SST有较大的差异，其中CFSR_6h试验模拟的全球年平均SST值为18.61℃，与观测（18.41℃）最为接近，误差为0.2℃；CFSR_ Day试验模拟的全球年平均SST值为18.84℃，相对于观测的误差为0.43℃；CFSR_Mon试验模拟的全球年平均SST值为19.35℃，相对于观测的误差为0.94℃。该结果表明，采用高频次的外强迫模拟的SST更接近观测，高频外强迫对全球海洋影响的总体效应为冷却海洋，而低频外强迫对全球海洋的总体效应为加热海洋。在此基础上，分别计算了3组试验的全球月平均SST与观测值的相关系数，3组试验与观测的相关系数分别为0.78（CFSR_6h）、0.73（CFSR_Day）、0.66（CFSR_Mon），均通过了99%的显著性检验。该结果表明采用不同时间频次的外强迫模拟的海表温度具有相似的变化趋势，但是高频外强迫模拟的SSTA更加接近观测。

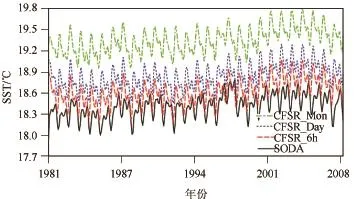
图1 SODA、CFSR_6h试验、CFSR_Day试验及CFSR_Mon试验的全球月平均SST随时间的变化

图2 CFSR_Day试验和CFSR_Mon试验分别与CFSR_6h试验的年平均SST差值（单位：℃）的空间分布

进一步对比了3组试验模拟的年平均SST的全球空间分布情况（图略）。3组试验均能较好的再现全球SST的整体分布特征。同时，3组试验模拟的年平均SST的分布也存在一定的差异。图2给出了CFSR_Day试验与CFSR_6h试验的年平均SST差值以及CFSR_Day试验与CFSR_6h试验的年平均SST差值的空间分布。相比于CFSR_6h试验模拟的年平均SST，CFSR_Day试验及CFSR_Mon试验模拟的年平均SST在太平洋海域及大西洋的西海岸海域偏高，但是偏高幅度不同。CFSR_Day试验的年平均SST最大偏高约1℃，而CFSR_Mon试验的年平均SST最大偏高超过3℃。在印度洋海域，CFSR_Day试验的年平均SST较CFSR_6h试验整体偏低，而CFSR_Mon试验的年平均SST在30°S以北海域偏低，而30°S以南海域偏高；在大西洋海域，除西海岸附近区域外，其他海域整体偏低，而CFSR_Mon试验的年平均SST在30°S—30°N之间偏低，其他海域偏高。该结果表明，不同时间频次的外强迫数据对不同的海域SST模拟的影响最主要机制可能不完全相同的。

3.2 海温的季节变化

3组试验均能很好的模拟出SST的季节变化特征。图3给出了CFSR_Day试验、CFSR_Mon试验的SST季节变化相对于CFSR_6h试验的差异。从图3可以看出，在赤道东太平洋海域，CFSR_Day试验及CFSR_Mon试验的SST季节变化相对于CFSR_6h试验的SST季节变化的振幅偏强，且CFSR_Mon试验在赤道东太平洋有1.5℃的正异常偏差；在赤道印度洋及大西洋海域，CFSR_Day试验及CFSR_Mon试验的SST季节变化相对于CFSR_ 6h试验的SST季节变化的振幅偏弱，但是总体差异相对的较小，均在正负0.5℃范围内。该结果进一步表明，不同时间频次外强迫对SST季节变化的影响在不同季节及不同海域的物理机制不尽相同。

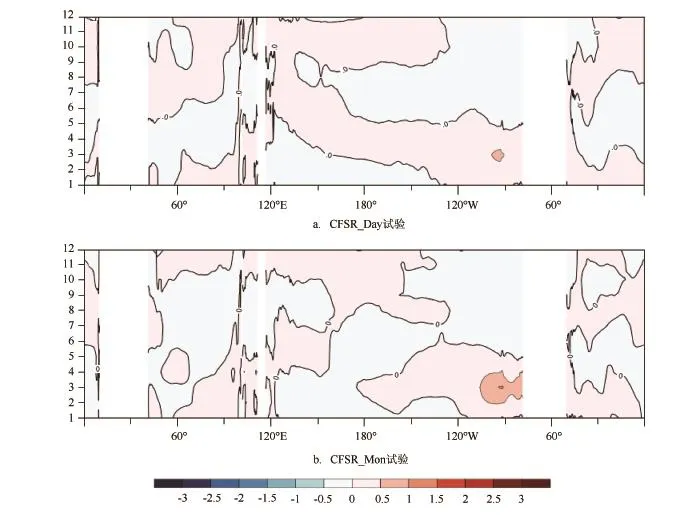
图3 CFSR_Day试验和CFSR_Mon试验分别与CFSR_6h试验SST季节变化的差值（单位：℃）随纬度-时间分布

3.3 海表温度的年际变化

3.3.1 热带太平洋海温年际变化

在年际尺度上，热带太平洋海温年际变化的最主要特征是ENSO[13]。当ENSO处于正位相时，海洋对应为El Niño事件；当ENSO处于负位相时，海洋对应为La Niña事件。通常用赤道东太平洋特定区域海温异常的平均值代表ENSO指数。目前国际上对ENSO指数的定义存在着较多的观点[14]，本研究中以Nino3.4指数为代表，研究采用不同时间频次外强迫数据强迫MOM4模式时模拟的ENSO的差异。

文中分别计算了SODA数据、CFSR_6h试验、CFSR_Day试验以及CFSR_Mon试验的Nino3.4指数，并对该指数进行了对比分析（见图4）。从图中可以看出，除了极个别年份（如2003—2004年）CFSR_Mon试验模拟的Nino3.4指数较观测偏大外，3组试验计算得到的Nino3.4指数与SODA数据计算得到的Nino3.4指数具有一致的变化特征，其与观测的Nino3.4指数的相关系数分别为：CFSR_6h试验计算的Nino3.4指数与观测的Nino3.4指数的相关系数为0.93；CFSR_Day试验计算的Nino3.4指数与观测的Nino3.4指数的相关系数为0.91；而CFSR_Mon试验计算的Nino3.4指数与观测的Nino3.4指数的相关系数则也达到了0.89。3组试验的Nino3.4的相关系数均通过了99%的信度检验。3组试验对几次强的El Niño事件均模拟的较好，如1982—1983年及1997—1998年，El Niño事件的爆发时间、持续时间及振幅均与观测较为一致。但是对于La Niña事件，在2000年以后，3组试验模拟的振幅均偏弱。以上结果表明，MOM4采用不同时间频次的CFSR外强迫数据均能较好的模拟出ENSO的变化特征，其中采用高时间频次的外强迫模拟的热带太平洋SST的年际变率更接近观测，但是这种优势不显著。

图4 逐月Nino3.4指数变化观测值（SODA）与CFSR_6h试验、CFSR_Day试验、CFSR_Mon试验的对比

图5 逐月DMI指数变化观测值（SODA）与CFSR_6h试验、CFSR_Day试验、CFSR_Mon试验的对比

3.3.2 印度洋海温年际变化

在热带印度洋区域，海温的年际变化的主要特征为印度洋海表温度异常（Sea SurfaceTemperature Anomaly，SSTA）呈现偶极子分布特征，也称为印度洋偶极子。Saji等[15]将赤道西印度洋（50°—70°E，10°S—10°N）和东南印度洋（90°—110°E,10°S—0°）海区平均的SSTA之差定义为印度洋偶极子指数（Dipole Mode Index，DMI）。

根据DMI的定义，分别计算了SODA数据、CFSR_6h试验、CFSR_Day试验以及CFSR_Mon试验的DMI指数，并进行了对比（见图5）。从图中可以看出，CFSR_6h试验、CFSR_Day试验以及CFSR_Mon试验模拟的DMI指数与SODA数据计算得到的DMI指数具有一致的变化特征。对于几次强的印度洋偶极子（Indian Ocean Dipole，IOD）正位相年份及负位相年份，3组试验均有较好的模拟，但是需要指出的是CFSR_Mon试验模拟的DMI指数在IOD较强的年份偏大。分别计算了3组试验模拟的DMI指数与SODA数据的相关系数，其中CFSR_6h试验模拟的DMI指数与SODA数据的DMI指数相关系数为0.9；CFSR_6h试验模拟的DMI指数与SODA数据的DMI指数相关系数为0.9；CFSR_6h试验模拟的DMI指数与SODA数据的DMI指数相关系数为0.85，这些相关系数均通过了99%的信度检验。该结果表明，MOM4采用不同时间频次的CFSR外强迫数据均能较好的模拟出印度洋偶极子的变化特征，其中采用高时间频次的外强迫模拟的印度洋SST的年际变化更加接近观测，但是优势同样不明显。

4 不同频次外强迫对海温影响的原因

4.1 不同频次外强迫的差异

3组试验的差异为使用了不同时间频次的外强迫数据，这些外强迫数据的气候态虽然相同，但是输入模式中的风应力及热力强迫存在着差异，这导致了海温、海流模拟的差异。

图6给出了1996—1997年间不同时间分辨率的沿赤道纬向风应力随时间的变化。从图中可以看出，3组不同时间频次的风应力随时间变化的趋势相对一致，但是在风应力的变率及大小方面存在较大差异。日平均及月平均对纬向风应力的影响主要有两个方面：一是降低了风应力的变率，二是减弱了风应力的强度。

3组试验辐射热通量的差异与风应力的差异类似。其中，3组试验的净辐射通量沿赤道的分布特征比较一致，但是随时间的变化存在较大的差异。逐6 h的净辐射通量在白天和夜晚存在较大的差异，海洋在白天吸收热量，夜晚放出热量，而通过日平均或者月平均，这种日变化的差异被消除了。同时，平均以后，低时间频次的净辐射通量的变率减小，尤其是月平均的辐射通量。

图6 1996—1997年3组试验中沿赤道纬向风应力（单位：N/m2）随时间的变化

4.2 影响机制

模式的SST的值在很大程度上取决于海洋中的垂向混合过程，通常垂直混合的强弱可以用混合层深度（Mixed Layer Depth，MLD）进行表征。MLD定义了湍流垂向混合所能达到的最大深度，其直接反映了上层海洋对各种外界强迫的响应强度，是刻画海洋上混合层的一个非常重要的物理参量。混合层的定义方法较多[16-18]，文中采用阈值的方法定义混合层深度，即：将与海表温度相差0.5℃所在处定义为混合层底。

图7 CFSR_6h试验、CFSR_Day试验及CFSR_Mon试验的全球月平均MLD随时间的变化

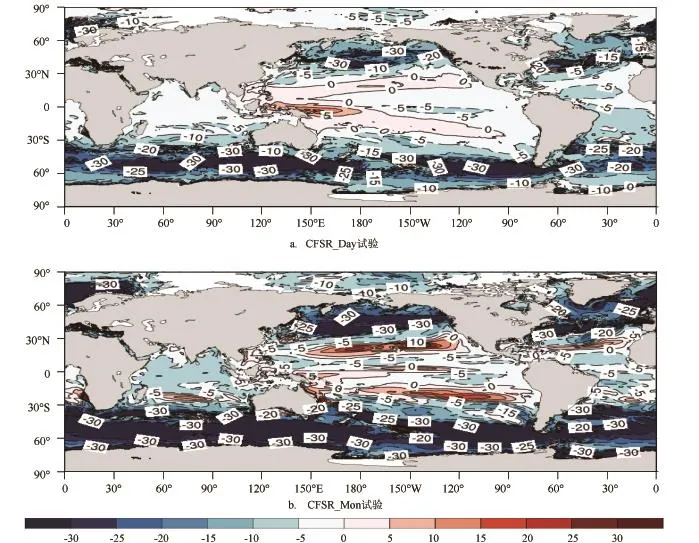
图8 CFSR_Day试验和CFSR_Mon试验分别与CFSR_6h试验的年平均MLD差值（单位：m）的空间分布

图7 给出了3组试验的全球月平均MLD随时间的变化。从图中可以看出，3组试验的全球月平均MLD随时间变化趋势非常一致，但是均值及振幅上存在较大的差异。3组试验的全球MLD的均值分别为61.1 m（CFSR_6h）、52.7 m（CFSR_Day）、47.3 m（CFSR_Mon）。随着外强迫时间频次的降低，MLD的均值呈现减小的趋势，即总体平均的垂直混合逐渐减弱。与之相对应的，3组试验的全球年平均SST随着外强迫时间频次的降低而增加。该结果表明：平均效应上，高频的外强迫可以加强海洋的垂向混合，从而起到对SST的降温作用。3组试验的振幅同样存在差异，CFSR_6h试验的MLD振幅异常极值比较大，序列的标准差达到了11.96 m，CFSR_Day试验的次之，CFRS_Mon试验的最小。3组试验的MLD的变化趋势较为一致，主要是因为时间平均对低频外强迫的影响较小。

图8给出了CFSR_Day试验、CFSR_Mon试验与CFSR_6h试验的年平均MLD差值的空间分布。CFSR_Day试验及CFSR_Mon试验模拟的MLD在全球大部分大洋上相比于CFSR_6h试验偏浅，但是在太平洋30°S—30°N之间，CFSR_Day试验及CFSR_Mon试验的MLD较CFSR_6h偏深，结合3组试验年平均SST的空间分布特征可以发现：在中高纬海域，CFSR_6h试验模拟的MLD偏深，温度偏低；而中低纬海域，CFSR_6h试验模拟的MLD偏浅，但是温度同样偏低。该结果表明，在中高纬地区造成海洋冷却的主要机制是垂直混合的加强，而在低纬区域及西边界流区域，垂直混合不是造成海洋冷却的主要机制，而平流过程及净热通量的加热作用可能是导致海温差异的更重要的机制。

5 结论

本文研究了不同时间频次的动力及热力强迫对全球大洋海温模拟的影响，分别设计了3组试验：CFSR_6h，CFSR_Day，CFSR_Mon，对比了这3组试验模拟的海温差异，并进一步的分析了这种差异产生的物理机制。

（1）通过与观测的海温对比，3组试验模拟的大尺度SST分布特征、SST的季节及年际变化等方面与观测较为一致。但是，CFSR_6h试验模拟的海温的全球年平均海温、全球月平均海温异常、平均SST的空间分布的各个方面比CFSR_Day试验及CFSR_Mon试验更加接近观测；

（2）3组试验模拟的全球年平均海温与观测分别相差0.2℃（CFSR_6h），0.43℃（CFSR_Day）以及0.94℃（CFSR_Mon）。不同时间频次外强迫对海温模拟的总体差异表现为高频外强迫具有冷却海洋的作用，而低频外强迫具有加热海洋的作用。在业务的海温预报中，为了提高海温预报技巧，非常有必要采用高时间频次的外强迫数据驱动海洋预报模式；

（3）3组试验采用的不同时间频次的外强迫数据具有相同的气候态，但是由于时间平均造成了低频外强迫的变率减小和强度减弱。前者的影响是3组试验模拟的海温的季节及年际变化相对一致，而后者导致了全球大洋垂直混合与热量收支的差异，进一步导致了海温大小的差异。在不同的海域，影响海温的主要物理过程存在一定的差异。在中高纬区域，主要通过垂直混合过程影响海温，而在低纬区域及西边界流区域，平流过程及外强迫的加热过程可能起着更为重要的作用。

本文研究了不同时间频次外强迫对全球大洋海温模拟的影响，探讨了不同外强迫对海温影响的机制，但是对于不同时间频次外强迫对不同海域的海温影响机制未能完全解决。造成该问题的原因主要有两方面：一是由于由于计算及存储条件的限制，试验未输出高频次的模拟结果，部分影响了物理机制的分析；二是在设计试验时，未将热力强迫及动力强迫分开进行试验，这导致在机制分析时无法分别讨论动力强迫及热力强迫的影响。未来将设计更多的试验，进一步讨论不同时间分辨率的动力强迫及热力强迫对海洋模拟的影响，更加细致的解释这种差异产生的物理机制，为未来建设业务化的海洋预测系统提供更加可靠的理论支持。

[1]Chen D K,Wang D P.Simulating the Time-Variable Coastal Upwelling During CODE 2[J].Journal of Marine Research,1990, 48(2):335-358.

[2]Large W G,Holland W R,Evans J C.Quasi-geostrophic Ocean Response to Real Wind Forcing:The Effects of Temporal Smoothing[J].Journal of Physical Oceanography,1991,21(7):998-1017.

[3]Chen D K,Rothstein L M,Busalacchi A J.A Hybrid Vertical Mixing Scheme and Its Application to Tropical Ocean Models[J]. Journal of Physical Oceanography,1994,24(10):2156-2179.

[4]Chen D K,Liu W T,Zebiak S E,et al.Sensitivity of the tropical Pacific Ocean simulation to the temporal and spatial resolution of wind forcing[J].Journal of Geophysical Research:Oceans,1999, 104(C5):11261-11271.

[5]Sui C H,Li X F,Rienecker M M,et al.The Role of Daily Surface Forcing in the Upper Ocean over the Tropical Pacific:A Numerical Study[J].Journal of Climate,2003,16(4):756-766.

[6]Kara A B,Hurlburt H E,Wallcraft A J,et al.Black Sea Mixed Layer Sensitivity to Various Wind and Thermal Forcing Products on Climatological Time Scales[J].Journal of Climate,2005,18(24):5266-5293.

[7]Casella E,Molcard A,Provenzale A.Mesoscale vortices in the Ligurian Sea and their effect on coastal upwelling processes[J]. Journal of Marine Systems,2011,88(1):12-19.

[8]Cardona Y,Bracco A.Enhanced vertical mixing within mesoscale eddies due to high frequency winds in the South China Sea[J]. Ocean Modelling,2012,42:1-15.

[9]Lee T,Liu W T.Effects of High-Frequency Wind Sampling on Simulated Mixed Layer Depth and Upper Ocean Temperature[J]. Journal of Geophysical Research:Oceans,2005,110(C5):C05002.

[10]Griffies S M,Harrison M J,Pacanowski RC,et al.A technical guide to MOM4[J].GFDL Ocean Group Technical Report,2004, 5:371.

[11]Saha S,Moorthi S,Pan H L,et al.NCEP Climate Forecast System Reanalysis(CFSR)SelectedHourlyTime-SeriesProducts, January 1979 to December 2010[R].Boulder,CO:Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory,2010.

[12]Carton J A,Chepurin G,Cao X H.A Simple Ocean Data Assimilation Analysis of the Global Upper Ocean 1950-95.Part II:Results[J].Journal of Physical Oceanography,2000,30(2): 311-326.

[13]黄荣辉.ENSO及热带海-气相互作用动力学研究的新进展[J].大气科学,1990,14(2):234-242.

[14]李晓燕,翟盘茂.ENSO事件指数与指标研究[J].气象学报, 2000,58(1):102-109.

[15]Saji N H,Goswami B N,Vinayachandran P N,et al.A dipole mode in the tropical Indian Ocean[J].Nature,1999,401(6751): 360-363.

[16]Kara A B,Rochford PA,Hurlburt H E.An Optimal Definition for Ocean Mixed Layer Depth[J].Journal of Geophysical Research: Oceans,2000,105(C7):16803-16821.

[17]Thomson R E,Fine I V.Estimating Mixed Layer Depth from Oceanic Profile Data[J].Journal of Atmospheric and Oceanic Technology,2003,20(2):319-329.

[18]范聪慧.多因素对海洋上混合层深度影响的数值模拟[D].北京:中国科学院研究生院(海洋研究所),2007.

Effects of different temporal resolution of wind and thermal forcing on simulated global ocean temperature

SHI Zhen，LI Xiang，LIU Na
（National Marine Environmental Forecasting Center,Key Laboratory of Research on Marine Hazards forecasting,State Oceanic Administration People’s Republic of China,Beijing 100081 China）

In this study,heat fluxes and wind stress with different temporal resolution are compared,and they are used as the upper boundary condition for a global oceanic general circulation model MOM4.Because of the time average,three experiments(CFSR_6h,CFSR_Day,CFSR_Mon)have the same climate characteristics,while differ in magnitude.The comparison between the simulations and observations reveals that the model SSTs have similar seasonal to interannual variability as the observed SST.But the magnitude of SSTs differ from observed SST within 1℃,the global mean SST in CFSR_6h is 0.74℃lower than in CFSR_Mon.In general,ocean temperature simulated with high frequency forcing is more similar with observation.The effect of high frequency forcing can cool the global ocean.In the mid-latitude and high-latitude area,high frequency forcing enhances vertical mixing to cool the ocean.But in the low-latitude area,the horizontal advection and heat flux may play more important roles to cool the ocean.

MOM4;temporal resolution;forcing;ocean temperature

P731.11

：A

：1003-0239（2016）06-0001-09

10.11737/j.issn.1003-0239.2016.06.001

2016-01-29

国家自然科学基金（41376016）；国家自然科学基金青年基金（41306008）。

史珍（1984-），女，助理研究员，博士，主要从事大气、海洋可预报性及海洋模式的研究。E-mail:shiz@nmefc.gov.cn