考虑边界条件变异和不同噪声的桥梁结构损伤识别
黄民水,王宁,卢海林
(1.武汉工程大学资源与土木工程学院,湖北武汉430073;2.阿尔伯塔大学土木与环境工程系,阿尔伯塔埃德蒙顿AB T6G 1H9,加拿大)
考虑边界条件变异和不同噪声的桥梁结构损伤识别
黄民水1,2,王宁1,卢海林1
(1.武汉工程大学资源与土木工程学院,湖北武汉430073;2.阿尔伯塔大学土木与环境工程系,阿尔伯塔埃德蒙顿AB T6G 1H9,加拿大)
运营期间桥梁结构在交通荷载、外界环境、材料劣化等因素的综合作用下,结构边界条件可能发生变化。边界条件对结构动力特性的影响显著,甚至远大于结构损伤的影响,损伤识别过程中如果忽略边界条件的变化可能会出现误判。本文介绍一种考虑边界条件变异的损伤识别方法,将边界条件的变化模拟成转动弹簧相对刚度系数的变化。首先,基于MATLAB建立了不同边界条件的结构数值模型,并利用ANSYS进行了模型验证。然后,通过改变转动弹簧的相对刚度系数,研究了不同边界条件对结构自振特性的影响。最后,将转动弹簧相对刚度系数和单元刚度折减系数作为损伤识别参数,基于布谷鸟算法进行了4种工况下的结构损伤识别,取得了较好的识别效果,并验证了不同噪声下本文方法的鲁棒性。
损伤识别;布谷鸟算法;边界条件变异;不同噪声;桥梁结构
桥梁结构的边界条件十分复杂,由于支座的摩阻力和非弹性变形,以及支座和伸缩缝的病害,结构的整体约束有一定的加强,并非理想的“铰接”或“刚接”。当前很多研究者在考虑环境因素对桥梁结构损伤识别的影响时,往往假定边界条件不发生变化[1-2]。然而,边界条件的变化可能导致结构的动力特性发生较大的变化,有时甚至大于结构损伤所造成的变化。文献[3]认为实际工程结构的动力特性与其边界条件密切相关。文献[4]在研究一块混凝土板的动力响应时,认为边界条件不发生变化,除了摩擦力外,混凝土板能自由运动。文献[5]在Z24桥的监测中发现温度降至冰点以下时,自振频率有较大的增加,认为是附近的冻土层改变了结构的边界条件。而现有的研究并未将这2类参数放在一起来进行损伤识别,往往假设边界条件不发生变化,导致识别数值计算困难,识别精度低,甚至造成误判。
布谷鸟算法(Cuckoo Search,CS),也叫杜鹃搜索,是由剑桥大学Yang和Deb于2009年提出的一种新兴启发算法[6],CS通过模拟某些布谷鸟的寄生育雏(Brood Parasitism,BP)来有效地求解最优化问题的算法,同时也采用了Levy飞行搜索机制,而非简单的随机游走,在整体优化问题中非常有效。最新研究表明,CS远比粒子群算法(Particle Swarm Optimization,PSO)和遗传算法(Genetic Algorithm,GA)有效,已有学者开始将CS应用于结构损伤识别[7-8]。本文将布谷鸟算法应用于考虑边界条件变异桥梁结构损伤识别,并进行了一定的改进,识别过程中考虑了噪声的影响,结果表明本文的方法识别效率高,具有较强的鲁棒性。
1 理论背景
桥梁结构的实际约束情况十分复杂,与交通荷载、环境温度、支座、伸缩缝等密切相关[9]。对基于环境激励的结构自由振动,可将边界条件的各类约束情况简化为线弹性支承,且主要考虑扭转约束发生变异对损伤识别的影响。文中取一简支梁模型进行损伤识别,在支座处采用无质量的、具有一定转动刚度的弹簧单元来模拟边界条件的变化[10]。简支梁的跨度为5 m,材料密度为7 800 kg/m3,弹性模量为200 GPa,截面面积为0.12m2,惯性矩为1.6×10-3m4。为验证计算模型的可靠性,进行了4种不同边界条件的计算分析,如图1所示。模型1,两端铰接;模型2,两端刚接;模型3,一端刚接,一端铰接;模型4,两端铰接,并有转动弹簧,相对刚度系数为k。

式中:kr为弹簧刚度系数;E为材料弹性模量;I为梁截面惯性矩;l为梁单元长度。
基于MATLAB编制了4种模型的有限元程序,获取结构的前4阶频率,并将计算结果与ANSYS计算结果进行了比较,如表1所示。可以看出,计算结果非常接近,最大偏差仅为1.77%。因此,可以认为本文的计算模型可靠,可用于后续的结构损伤识别。

图1 4种不同边界条件的结构模型

表1 本文计算的自振频率和ANSYS的结果对比
2 不同边界条件对动力特性的影响
文中假定了2类边界条件:
1)条件1:右端铰接(k右=1×10-15),左端转动弹簧相对刚度系数从1×10-15变化至1×106。
2)条件2:右端刚接(k右=1×1015),左端转动弹簧相对刚度系数从1×10-15变化至1×106。
转动弹簧相对刚度系数对竖向1~4阶频率的影响如图2所示。可以看出,在2种条件下,当相对刚度系数>1 000时,左端可视为刚接,当相对刚度系数<1/1 000时,左端可视为铰接。

图2 转动弹簧相对刚度系数对结构自振频率的影响
3 CS算法
3.1 布谷鸟的繁殖行为
布谷鸟不仅能发出好听的叫声,且有极具侵略性的繁殖策略。一些布谷鸟,比如Ani和Guira等,将自己的卵产在一些公共鸟巢里,并将其他鸟卵推出鸟巢,以增加自己鸟卵的孵化概率。而另有一些种类的布谷鸟直接将卵产在宿主鸟巢里来进行孵化。宿主鸟类会与入侵的布谷鸟发生直接冲突,如发现自己鸟巢内的卵不是自己的,它们要么将外来卵直接扔掉,要么放弃鸟巢,在别处另筑新巢。随着不断的进化,一些布谷鸟,比如雌性的寄生布谷鸟Tapera还能产出颜色、形态和宿主鸟卵非常相似的卵,能减少它们的卵被宿主鸟抛弃的可能性,进而会增加自身的孵化概率。
一些布谷鸟经常选择宿主鸟刚产卵的鸟巢产卵,且在一般情况下,布谷鸟卵的孵化时间比宿主鸟卵的孵化时间要稍早一点,一旦第1个布谷鸟卵孵化出来,其本能行为就会将宿主鸟卵推出鸟巢,以增加幼鸟的喂食概率。另外,布谷鸟的幼鸟还可以模仿宿主鸟幼鸟的叫声,以进一步获得更多的喂养机会[11]。
3.2 莱维飞行(Levy flight)
布谷鸟以随机或类似随机的方式寻找适合产卵的鸟巢位置,为了模拟布谷鸟寻巢的方式,设定以下3个理想的状态[11]:
1)每只布谷鸟每次只产1个卵,并且把它放在随机选定的鸟巢内;
2)具有高质量鸟卵的巢会延续到下一代;
3)宿主鸟巢的数量n是不变的,而布谷鸟的鸟卵有一定的概率(Pa∈[0,1])被宿主鸟发现,在这种情况下,宿主鸟就会把布谷鸟的鸟卵扔掉或者抛弃自己的巢到另外的地方重新建巢。
3.3 基本布谷鸟算法
采用莱维飞行的全局随机游动如下
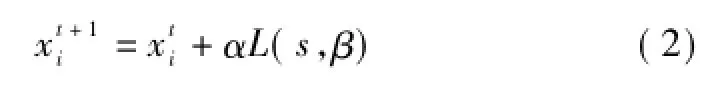
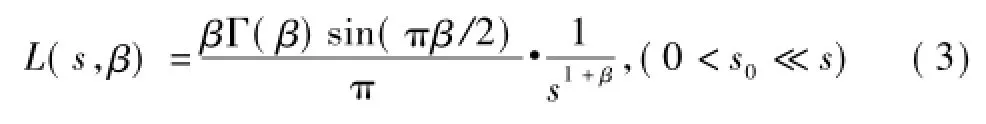
式中:β为莱维飞行的索引值,0<β≤2;Γ为标准Gamma函数;s0为最小步长。
3.4 步长的改进
由于基本随机搜索步长固定,局部搜索能力较差,故文中采用自适应步长进行搜索,步长随着迭代次数的增加而发生自适应的变化。在迭代初期,采用大步长,避免搜索陷入局部最优。随着迭代次数的增加,步长不断地减小至最小值,确保算法后期能快速收敛,顺利获取全局最优解。
一般,随机游走是1个马尔科夫链,其下1个位置或状态仅取决于当前位置和转移概率。为应用基于Mantegna算法的莱维飞行,自适应步长s'如式(4)~(6)所示


式中:u和v服从标准正态分布;σu和σv为标准差; fbest为适应度最优值。
3.5 适应度函数
采用结构前4阶自振频率和振型构建适应度函数,由于在桥梁结构振动测试中,自振频率相对模态振型更可靠,故采用较大的权重系数F[12]。
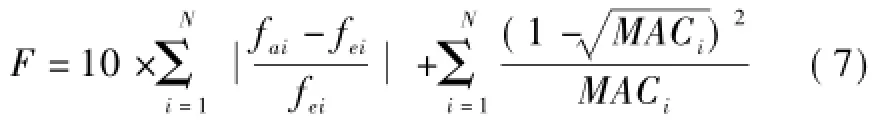
式中:fai和fei分别为i阶理论和试验自振频率;MACi为模态置信度,分别为i阶理论和试验竖向振型;N为模态阶数。
4 损伤识别
4.1 无噪声的结构损伤识别
从前文可以看出,弹簧的相对刚度系数在[0,1 000]变化:相对刚度系数>1 000时,可视为刚接,无损伤;相对刚度系数为0时,可视为铰接,100%损伤。对于桥梁结构,特别是采用钢支座的桥梁,如果在各种因素的作用下,比如锈蚀,可能会在梁端附加一定的转动约束,从而约束支座的转动。为简化起见,考虑较为理想的情况,即边界条件仅为刚接或铰接。假设单元8#,9#的刚度折减系数为0.2,在模型4的基础上,根据左、右转动弹簧相对刚度系数变化,建立了4种损伤工况,如图3所示。

图3 损伤模型
1)工况1:梁部为两点损伤,左、右转动弹簧相对刚度系数均为0。
2)工况2:梁部为两点损伤,左转动弹簧相对刚度系数为0,右转动弹簧相对刚度系数为1 000。
3)工况3:梁部为两点损伤,左转动弹簧相对刚度系数为1 000,右转动弹簧相对刚度系数为0。
4)工况4:梁部为两点损伤,左、右转动弹簧相对刚度系数均为1 000。
将左、右转动弹簧相对刚度系数和16个梁单元的刚度折减系数作为识别参数。采用基于MATLAB开发的程序进行模态分析,获取损伤前后的“实测”动力数据,取前10阶固有频率及振型向量作为“实测”数据。采用前文所述的布谷鸟算法进行损伤识别,鸟巢规模为100,发现概率为0.25,适应度函数达到预设值或进化代数达到2 000时,迭代终止。4种工况下的识别结果如图4和表2所示。从图4可以看出,仅8#和9#被识别出损伤,损伤值为0.20,与预设值非常吻合。从表2可以看出,4种工况下,左、右转动弹簧相对刚度系数均被很好地识别出来,识别值和初始值非常吻合。
4.2 噪声对损伤识别的影响

图4 损伤单元识别结果
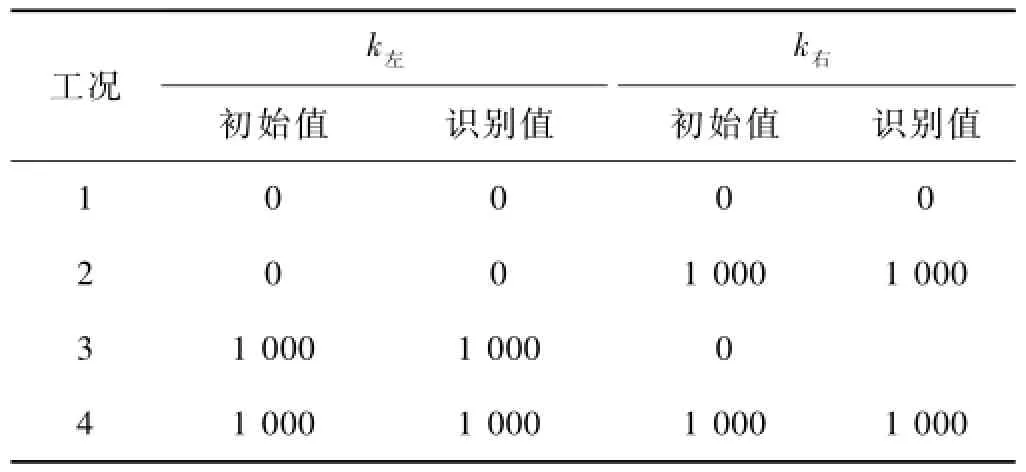
表2 左右转动弹簧相对刚度系数识别结果
在无噪声情况下,文中方法具有较好的识别效果。为了验证本文方法的鲁棒性,在振型数据里添加了随机噪声和高斯白噪声。
4.2.1 随机噪声
随机噪声(Random Noise),又称背景噪声,是由随机产生的、在给定时间内不能预测的噪声。由于在实际振动测试中,高阶模态往往不如低阶模态可靠,故仅考虑了前4阶模态,同时,自振频率的测试精度高于振型,故仅在振型中施加不同程度的随机噪声。假设第k次测试中的j阶振型的第φij分量被噪声污染:
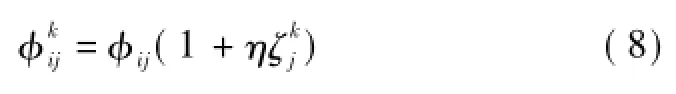
在工况1中,施加了4种不同程度的随机噪声,3%,5%,10%和20%。识别结果如图5所示,可以看出,损伤的位置和程度均被准确识别出来。
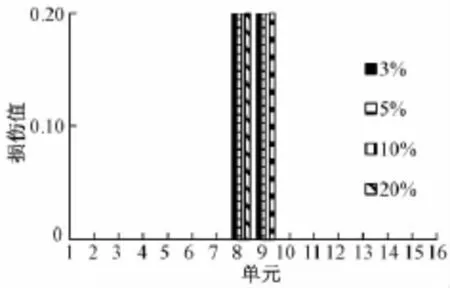
图5 随机噪声作用下的损伤识别结果
4.2.2 高斯白噪声
高斯白噪声(White Gaussian Noise)的概率密度函数满足正态分布统计特性,且它的功率谱密度函数是常数。假设第k次测试中的i阶振型的j阶分量φ被ij噪声污染[13]:

式中:φmax,j为j阶振型的最大分量,对归一化振型则取1;randn为matlab中的函数,生成均值为0,方差为1的随机数;ρjd为噪声水平。
ρjd和信噪比SNR的对应关系如表3所示。

表3 ρjd和信噪比SNR的对应关系
在工况1中分别考虑了7种信噪比,分别为80,60,40,20,10,5和0 dB,识别结果如图6所示。可以看出,当信噪比为0,5 dB时,可得到结构的损伤位置,损伤程度的最大误差分别为4.7%和5.15%;当信噪比为10 dB及以上时,损伤程度最大误差为0.85%。因此,在不同噪声水平下,均能准确地识别出结构的损伤位置,当噪声水平较高时,最大误差为5.15%。可以看出,文中方法具有较强的鲁棒性。

图6 高斯白噪声作用下的损伤识别结果
5 结论
基于布谷鸟算法研究了考虑边界条件变异的桥梁结构损伤识别,并验证了不同噪声下的鲁棒性,主要结论如下:
1)边界条件对桥梁结构损伤识别有明显的影响,文中将边界条件的变化模拟成转动弹簧相对刚度系数的变化,并将转动弹簧相对刚度系数和单元刚度折减系数共同作为损伤识别的参数。
2)采用布谷鸟算法进行了优化,并对步长进行了改进,优化过程中步长自适应变化,并基于结构自振频率、振型构建了适应度函数。
3)基于MATLAB编制了有限元分析程序,对一简支梁数值算例进行了损伤识别,能有效地确定弹簧相对刚度系数和损伤位置、程度,识别精度良好,并考虑了随机噪声和高斯白噪声对损伤识别精度的影响。结果表明,本文方法具有较强的鲁棒性,可用于实际工程的损伤识别。
[1]RAVANFAR S A,RAZAK H A,ISMAIL Z,et al.A Two-step Damage Identification Approach for Beam Structures Based on Wavelet Transform and Genetic Algorithm[J].Meccanica,2016,51(3):635-653.
[2]李顺龙,李惠,欧进萍,等.考虑温度和风速影响的桥梁结构模态参数分析[J].土木工程学报,2009,42(4):100-106.
[3]刘玉明,易伟建.一种识别结构系统边界条件的新方法[J].湖南大学学报(自然科学版),1999(4):99-107.
[4]XIA Y,HAO H,ZANARDO G,et al.Long Term Vibration Monitoring of an RC Slab:Temperature and Humidity Effect[J].Engineering Structures,2006,28(3):441-452.
[5]PEETERS B,DE ROECK G.One-year Monitoring of the Z24-Bridge:Environmental Effects Versus Damage Events[J].Earthquake Engineering and Structural Dynamics,2001,30 (2):149-171.
[6]YANG X S,DEB S.Cuckoo Search Via Le'vy Flights[C]// Proceedings of World Congress on Nature and Biologically Inspired Computing(NaBIC 2009).USA:IEEE Publications,2009:210-214.
[7]王利英,杨绍普,赵卫国.基于改进布谷鸟搜索算法的架桥机结构损伤识别[J].北京交通大学学报,2015,37(4): 168-173.
[8]徐浩杰,刘济科,吕中荣.改进的布谷鸟算法在结构损伤识别中的应用[J].应用力学学报,2016,33(3);523-528.
[9]施洲,赵人达.基于模态参数考虑边界条件变异的桥梁结构损伤识别[J].应用力学学报,2012,29(2):191-196.
[10]ZHOU S L,SONG W.Variation of Modal Properties by Combined Effects of Temperature and Boundary Condition[C]// Proceedings of SPIE 9435,Sensors and Smart Structures Technologies for Civil,Mechanical,and Aerospace Systems.USA: SPIE Publications,2015:94352L.
[11]YANG X S,DEB S.Nature-inspired Metaheuristic Algorithms[M].2nd.United Kingdom:Luniver Press,2010.
[12]黄民水,吴玏,朱宏平.噪声影响下基于改进损伤识别因子和遗传算法的结构损伤识别[J].振动与冲击,2012,31 (21):168-174.
[13]曹晖,林秀萍.结构损伤识别中噪声的模拟[J].振动与冲击,2010,29(05):106-109.
Damage Identification of Bridge Structure Considering Variation of Boundary Conditions and Different Noises
HUANG Minshui1,2,WANG Ning1,LU Hailin1
(1.School of Resource and Civil Engineering,Wuhan Institute of Technology,Wuhan Hubei 430073,China; 2.Department of Civil and Environmental Engineering,University of Alberta,Edmonton Alberta AB T6G 1H9,Canada)
During the operation period,under the influences of traffic loading,external environment and material deterioration,the boundary condition of bridge structure may change.T he influence of boundary condition to structural dynamic properties is significant,which is even more than that induced by damage in the structure.If boundary condition is assumed to be unchanged during the process of damage identification,false results may occur.A damage identification method was introduced in this paper,which considered the variation of boundary condition.Firstly,the numerical models with different boundary conditions were set up based on M AT LAB and the results were validated by using ANSYS.Secondly,the influence of boundary condition to structural dynamic properties was studied by changing the relative stiffness coefficient of rotational spring.Finally,the stiffness coefficient of the rotational spring and stiffness reduction coefficient of elements were adopted as identification parameters.T he structural damage identification was carried out based on the algorithm of Cuckoo Search(CS)under four conditions.T he results show that the identification performance is very well and the robustness of the proposed method is validated under different noises.
Damage identification;Cuckoo Search;Variation of boundarycondition;Different noises;Bridge structure
U441
A
10.3969/j.issn.1003-1995.2016.12.04
1003-1995(2016)12-0012-05
(责任审编郑冰)
2016-07-01;
2016-11-01
国家留学基金(201508420074);国家自然科学基金(51378404);湖北省自然科学基金(2014CFB773)
黄民水(1976—),男,副教授,博士。
卢海林(1965—),男,教授,博士。

