水力作用下陡倾顺层岩质斜坡的倾倒破坏
林必挺,袁宝远,邹 凯,桂永庆
(河海大学地球科学与工程学院,南京 211100)
水力作用下陡倾顺层岩质斜坡的倾倒破坏
林必挺,袁宝远,邹 凯,桂永庆
(河海大学地球科学与工程学院,南京 211100)
陡倾顺层岩质斜坡的倾倒变形破坏与水力因素密切相关。将陡倾顺层斜坡的岩层概化为受自重及水力作用的悬臂梁。通过建立陡倾顺层岩质斜坡不同阶段水力作用下倾倒变形破坏的力学模型,揭示了陡倾顺层岩质斜坡的倾倒变形破坏过程。通过定量分析滑移面中产生的静水压力及后缘拉裂缝中的充水高度对坡体稳定性的影响,得出坡体稳定性系数及临界充水高度的表达式。结果表明:水力作用产生的倾倒力矩是引起该类斜坡发生倾倒变形与破坏的重要原因,坡体的稳定性系数降低亦是由水力作用引起的,排水是防治该类斜坡倾倒变形破坏的首要措施。
陡倾顺层岩质斜坡;水力作用;力学模型;倾倒破坏;坡体稳定性
0 引言
倾倒变形是河谷地区层状岩质斜坡破坏的一种主要形式,岩体在外动力地质作用或者人工活动下发生蠕动变形而向临空面一侧做“悬臂梁弯曲”产生的“点头哈腰”现象。
一般而言,陡倾顺层岩质斜坡是比较稳定的,但在众多工程活动中发现陡倾顺层岩质斜坡也能发生倾倒变形。国内学者任光明等提出发生陡倾顺层倾倒变形破坏的有利条件为:(1)岩性上多发育在力学差异较大,软硬相间的互层状岩体中或者力学性质较差的软岩中;(2)岩层倾角较陡,构成斜坡的岩层倾角一般大于60°;(3)陡倾顺层岩质斜坡倾倒变形破坏多发育在高陡斜坡及快速下切的河谷中[1]。谭儒蛟在其研究综述中提到国外学者Cruden和Hu在 Alberta发现了贯通性不连续面倾向与坡向一致但倾角比坡脚要陡的斜坡中存在大量的倾倒变形现象,即顺层倾倒,并将其分为(1)块状弯曲倾倒;(2)多重块体倾倒;(3)人字型倾倒三种基本类型[2]。李天扶提出水压力产生的额外倾倒力矩是某些陡倾顺层岩质斜坡发生倾倒变形破坏的重要因素,并改进了Duncan C.Wyllie的倾倒变形体水压力计算模型,给出了水压力对岩层产生的倾倒力矩的表达式[3]。
本文通过对陡倾顺层岩质斜坡倾倒变形破坏过程中各个阶段水压力产生的倾倒力矩进行力学分析,分析各个阶段的倾倒变形破坏特征,并给出合理的表达式。在仅考虑静水压力对滑体的影响情况下,推导出后缘张裂缝充水高度及稳定性系数表达式,认为在斜坡倾倒破坏-滑移面贯通阶段,当后缘张裂缝充水高度达到临界高度时倾倒变形体将发生滑移[4]。目前,对于陡倾顺层岩质斜坡倾倒变形破坏问题研究较少,缺少外界因素特别是水力作用对陡倾顺层岩质斜坡倾倒变形破坏的定量分析,本文从力学角度完善了顺层倾倒破坏发生的模式,具有一定的实际意义。
1 陡倾顺层岩坡倾倒变形破坏演化过程
对于陡倾顺层岩体组成的斜坡,在河谷下切过程中,伴随着斜坡岩体的卸荷回弹,岩体发生松弛变形,岩体力学性质降低。斜坡的原始应力场发生变化,靠近坡面,最大主应力方向平行于坡面,最小主应力垂直于坡面。结果是坡脚处形成剪应力集中区,坡缘处形成拉应力集中区。岩层间因松弛变形产生的张裂隙使得降雨、地表水等更易进入坡体内,裂隙中的水产生的水压力为岩层向临空面方向倾倒提供了相当大的倾倒力矩,岩层间水头差的存在使得岩层向临空面方向发生牵引式的陆续倾倒[5]。其变化发展可以概括分为4个阶段。
(1)卸荷松弛,岩层开裂阶段:斜坡变形初期,在河谷下切过程中斜坡岩体卸荷回弹的作用下,岩体发生松弛变形,岩体完整性降低,在平行坡面的最大主应力作用下岩层面张开。
(2)坡脚初始倾倒,裂纹产生阶段:岩层面的开裂使得水进入坡体内成为可能,位于坡脚的岩层由于临空面方向没有支撑,在后方水压力产生的倾倒力矩与平行坡面的最大主应力作用下发生初始倾倒变形,岩层由于弯曲倾倒产生裂纹。
(3)板梁弯曲,倾倒变形扩展阶段:随着坡脚初始倾倒变形加剧,坡脚处岩层裂缝中的水部分排出,使得水压力迅速下降,引起中后部岩体水头差增大,进一步增加了倾倒力矩,中后部岩体开始发生牵引式的弯曲倾倒变形,因岩层间相对滑移弯曲受阻,在最大弯曲部位产生不连续折断面。
(4)倾倒破坏,滑移面贯通阶段:随着斜坡岩层弯曲变形加剧,水不断从岩层裂缝中排出,水头差不断增大,加剧岩体倾倒变形,当最大弯曲部位折断面相互贯通形成滑移面时,即形成滑移-拉裂形滑坡。由于岩层弯曲的发展,作用于岩层的力矩也随之增大,因此这类变形一旦发生,将显示明显的累进性变形特征[6]。岩层张裂缝中的水体最终集中至滑体后缘张裂缝与滑移面中,以倾倒力矩与垂直于滑动面向上的静水压力的形式影响滑体的稳定性(图1)。

图1 陡倾顺层岩坡破坏过程Figure 1 Steeply dipped bedding rock slope deformation and failure process
2 水力影响下陡倾顺层岩坡力学模型分析
2.1 未折断板梁力学模型
板梁未发生折断前,其与下部岩体为一整体,仅在侧面受到水压力作用,由于岩层开裂,潜在折断面上部的板梁之间可以看作没有相互作用力,单个板梁仅受到自重及侧面水压力作用。选取坡体内任意板梁,将其概化为矩形建立力学模型(图2)。
图2中Wi为潜在折断面上部第i块板梁所受重力,作用点位于板梁重心;Vi与Vi-1分别为i块板梁后侧与前侧受到的水压力;hi与hi-1分别为板梁两侧充水斜高;yi及yi-1分别为板梁两侧高度;di第i块板梁宽度;li为第i块板梁底面的滑弧长度;αi为第i块板梁底面的倾斜角;水的重度为γw。
为计算简便,板梁重心位置位于其中点处,水压力合力作用点位于水位斜高的下三分点处。则板梁两侧受到的水压力表达式为:

所有外力以板梁右下脚O点为矩心取矩,则板梁的倾倒力矩仅由水压力产生,倾倒力矩表达式为:


图2 未折断任意板梁力学模型Figure 2 Mechanical model of unbroken discretional plate beam
抗倾倒力矩由板梁所受到的重力产生,得到抗倾倒力矩为:

则由(2)、(3)两式得任意板梁合力矩表达式为:
当板梁所受的合力矩Mi>0板梁将开始发生倾倒变形。
根据前文分析,天然状态下位于斜坡中后部的板梁在坡脚未发生初始倾倒前处于平衡状态,即Mi=0,板梁不发生倾倒变形。对于坡脚的板梁由于其临空面方向没有支撑,将发生初始倾倒变形,由坡脚开始向中后部发生累进式的变形。坡脚板梁仅后侧有水压力作用(图3)。

图3 坡脚第一块板梁力学模型Figure 3 Mechanical model of slope toe first plate beam
坡脚第一块板梁受到后侧水压力为:

倾倒力矩为:
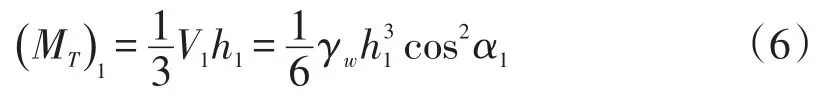
抗倾倒力矩为:

由(6)、(7)两式得合力矩为:

从合力矩表达式可以看出,由于坡脚板梁前侧没有水压力提供抗倾倒力矩,相较于后方板梁,坡脚第一块板梁承受更大的力矩,更易于发生倾倒变形,也就说明了倾倒变形往往从坡脚开始发生的原因。
折断板梁相较于未折断板梁而言,由于底面折断带的形成,必然会有岩层裂缝中水位的下降,由此引起未折断板梁前侧水压的降低。如图4所示,当第i块未折断板梁前方板梁发生折断后,其前侧水位部分下降,水压力降低,如此便增加了未折断板梁侧面的水头差。V′i-1为未折断板梁前侧水位降低后的水压力,h′i-1为其斜高,水位降低后力矩分析如下。
水位下降后未折断板梁的新倾倒力矩由板梁两侧水头差产生,其表达式为:

抗倾倒力矩仍为(MR)i不变,得到新的合力矩表达式:

与式(4)表达式相比较,由于hi>h′i-1,故M′i>Mi,即当板梁前侧水位下降时会导致板梁受到的合力矩增大,加剧倾倒变形的发展。

图4 折断板梁引起的水位下降Figure 4 Water level lowering caused by broken plate beam
2.2 折断板梁力学模型
折断板梁分为部分折断与完全折断两种情况考虑。折断带的形成使得岩层裂缝中的水进入到折断带中,折断带中的水以底面静水压力的形式对板梁提供倾倒力矩。由于各板梁折断程度不一,更难以确定,本文考虑部分折断板梁底面产生的静水压力时按照完全折断时的情况处理,这样处理的优点在于底面静水压力均按所能提供的最大值计算,产生的倾倒力矩较大,考虑稳定性时计算结果偏于保守。
引文[3]中李天扶对板梁底面的静水压力及其产生的倾倒力矩的计算给出了较为合理的方法,如图5所示。
图5中Hi与Hi-1分别为第i块板梁与第i-1块板梁后侧底端水头高;底面水压力分布为梯形,并以Ui表示,其作用线通过梯形重心垂直作用于底面上,将梯形沿对角线分为两个三角形分别计算水压力与倾倒力矩,上三角形水压力为Ui1,下三角形水压力为Ui2。由于板梁长细比很高,底宽可近似看作di。

图5 底面水压力计算模型Figure 5 Computational model of underside water pressure
则底面水压力为:

底面水压力产生的倾倒力矩(MU)i为:
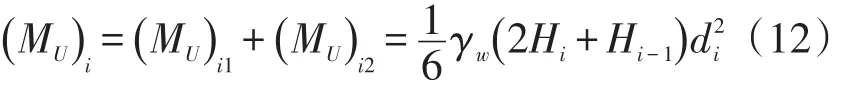
当板梁完全折断后,岩层间裂隙水大部分流至底部折断面,故对于完全折断板梁可不考虑侧水压力。部分折断板梁由于底部折断面未贯通,需要考虑后侧水压与底面水压的作用(图6)。
图6中H′i与H′i-1分别为部分折断板梁后侧底端与前侧底端水头高,Pi为部分折断板梁后侧水压力,h′i为充水斜高,板梁前侧水压力为零。
根据分析得到部分折断板梁侧面水压与底面水压的表达式:

相应地,侧面水压力与底面水压力产生的倾倒力矩表达式为:
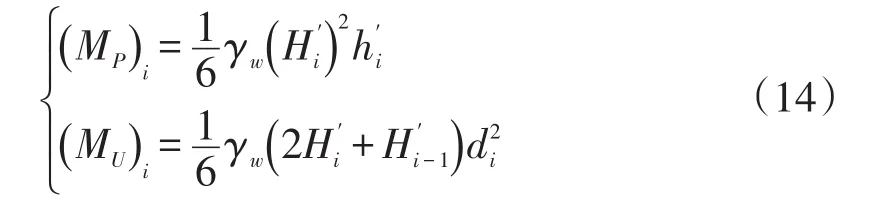
板梁所受重力仍然产生倾倒力矩与抗倾倒力矩两部分,整理得板梁受到的倾倒力矩与抗倾倒力矩分别为:

由上式得板梁受到合力矩为:

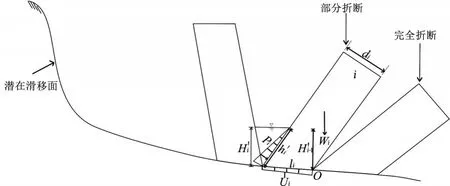
图6 部分折断板梁力学模型Figure 6 Mechanical model of partial broken plate beam
底面水压力不仅增加了板梁下滑力,亦增加了板梁的倾倒力矩,重力平行于坡面的分力随着板梁由倾向坡内转为倾向坡外,产生的力矩由抗倾倒力矩变为倾倒力矩,使部分折断板梁倾倒变形加剧直至完全折断。
通过上文的计算分析可见,陡倾顺层岩质斜坡的倾倒变形破坏与水力学因素紧密相关,岩层裂隙中的水产生倾倒力矩使原先难以发生倾倒变形的岩体逐渐向临空面方向倾倒。坡脚发生的初始倾倒变形引起中后部岩层间裂隙水的水位下降,增加了岩体水头差,引起牵引式的陆续倾倒。已发生倾倒变形的岩体随着底面水压力的增加以及水头差的继续加大,倾倒变形现象加剧。因此这类倾倒变形一旦发生,就具有很明显的累进性变形特征。
3 水力影响下倾倒变形岩体稳定性及失稳判剧
当各板梁均完全折断,即倾倒变形体形成贯通性的折断面时,则倾倒变形阶段结束,此时倾倒变形体由于有贯通折断面的存在,其整体即为一潜在滑体,贯通折断面为滑移面。对于滑体的失稳破坏,在不考虑地震等动荷载情况下,水力学因素仍然是滑体失稳破坏的重要因素。滑体中的水分布于后缘拉张裂缝与滑移面中,后缘张裂缝中的水以静水压力的形式作用于滑体;滑移面中的水对滑体的作用力可分为静水压力与动水压力。舒继森等的研究表明,动水压力对斜坡稳定性的影响很小,而且随张裂缝中水深变化不大;而静水压力对斜坡稳定性的影响较大,斜坡的稳定系数在静水压力的影响下随张裂缝中水深的变化而急剧下降[7]。因此本文仅考虑后缘张裂缝中的静水压力与滑移面中静水压力对滑体稳定性的影响(图7)。
陡倾顺层岩质斜坡倾倒破坏的滑移面通常为弧形,因此为使得分析结果具有代表性,将滑移面近似看作一圆弧面。滑体共分为n块板梁,第i块板梁后侧底端水头高为Hi,板梁传给滑移面上的质量为Wi,它可以分解为垂直于滑移面的法向力Ni与切于滑移面的切向力Ti;第i块板梁底面滑弧面凝聚力为ci,内摩擦角为φi;V为后缘张裂缝中的静水压力。设圆弧的圆心为O(即矩心),半径为R。
Ni可使板梁在滑动面上产生摩阻力Nitan φi,对滑体起着抗滑作用,凝聚力ci亦起到抗滑作用;而滑移面上的静水压力与后缘张裂缝中的静水压力起到下滑作用。则其力学表达式为:

斜坡稳定安全系数FS定义为抗滑力矩与下滑力矩之比。对单个板梁,抗滑力矩由垂直于滑移面的垂向分力Ni与凝聚力ci产生,对每一板梁进行分析可得总的抗滑力矩为:


图7 滑体力学模型Figure 7 Mechanical model of landslide mass
下滑力矩由切于滑移面的切向力Ti及后缘张裂缝中静水压力V产生,则总的下滑力矩为:

则滑体在自重及水力作用下的稳定性系数为:

将式(17)Ni,Ui,Ti带入式(20)得稳定性系数表达式为:

令式(21)等于1,即可求出极限平衡状态下后 缘张裂缝充水高度Hc表达式:

从式(21)可以看出后缘张裂缝充水高度与滑移面凝聚力、内摩擦角、板梁宽度、质量以及滑移面形态等相关。充水高度的大小直接影响对滑体产生的下滑力,并使得滑移面上的静水压力大小产生变化,从而影响抗滑力的大小。从式(20)、(21)可以看出,当充水高度Hn>Hc,分母部分后缘张裂缝静水压力增大,分子部分滑移面上静水压力的增大,减少了滑体对滑移面的有效压力,间接导致滑体在滑动面上的摩阻力减小,斜坡失稳;Hn<Hc,斜坡处于稳定状态;Hn=Hc,斜坡处于极限平衡状态。因此在其它条件相同情况下,后缘张裂缝充水高度决定了滑体稳定性。
4 算例分析
以某一陡倾顺层岩质边坡倾倒破坏形成的倾倒滑移体为算例进行分析。坡体由灰黑色含炭质板岩组成。边坡各计算参数如下:岩体天然重度为26.79 kN/m3,饱和重度为27.12 kN/m3。天然状态下滑移面的抗剪强度参数为:黏聚力c1=20 kPa,内摩擦角φ1=20°;饱和状态下滑移面的抗剪强度参数为:黏聚力c2=16 kPa,内摩擦角φ2=18°。剪出口到后缘坡面的高度57.5 m,后缘张裂缝深度为25 m,滑弧长度l=180 m,滑体后缘宽度L1=55 m,前缘宽度L2=175 m,平均宽度为L=90 m,滑移面平均倾角α=16°,单个板梁厚度约0.1m,滑体的潜在方量为65×104m3。
天然状态下滑体不受水压力的作用,因此在用式(20)计算稳定性系数时,不考虑水压力的计算。代入数据得天然状态下稳定性系数为:

天然状态下滑体处于稳定状态,发生滑坡的可能性低。当边坡受地下水或地表水充分浸润后,岩体力学性质发生变化。则饱和状态下(仅考虑岩石力学性质变化,不考虑水力作用)稳定性系数为:

饱和状态下滑体相对于天然状态稳定性系数降低了0.14,稳定性系数的降低来自于岩体本身性质的降低以及滑移面抗剪强度的降低。当遇强降雨或者地下水位上升时,考虑滑移面及后缘张裂缝中充满水,则此时稳定性系数的计算应同时考虑饱和状态及充水状态。值得注意的是由于公式的计算是基于二维平面的,此时水压力是线分布力,而实际上的水压力应是面力,故在计算滑体水压力时应乘以水压力作用宽度,结果如下:

即滑移面与滑体后缘张裂缝充满水状态较天然状态稳定性系数降低了0.31,较饱和状态稳定性系数降低了0.17。可见水力作用对滑体性质的恶化是较为明显的,在滑移面及后缘张裂缝静水压力驱动下将发生滑坡破坏。后缘张裂缝中充水高度不同则滑体稳定性也会不同。表1为后缘张裂缝中不同充水高度对应的稳定性系数。

表1 不同充水高度对稳定性系数的影响Table 1 Impact on stability coefficient under different water filling heights
将表1数据绘成折线图,如图8所示可以得出临界充水高度Hc=9.7 m,与用式(22)计算结果相同,验证了公式的合理性。后缘张裂缝中充水高度的变化实际上对稳定性系数影响不大,且随着充水高度的升高,稳定性系数并非呈线性下降,而是随充水高度的增加,稳定系数降低速度逐步加快,其原因在于张裂缝中水量的增加加速溶解了岩石中的可溶性矿物,使岩石软化,力学性质降低。滑移面中的静水压力通过降低滑移面抗剪强度参数及减小滑体的有效压力,能较大程度的影响滑体稳定性,在治理这类滑坡时应当重点考虑滑移面上的排水措施。

图8 充水高度—稳定性系数关系曲线Figure 8 Relationship between water filling height and stability coefficient
5 结论
(1)陡倾顺层岩质斜坡倾倒变形各阶段,岩层裂缝中的水通过水压力产生的倾倒力矩使岩层发生倾倒,坡脚处岩体的倾倒增加了中后部岩体的水头差,引起牵引式的破坏。
(2)水力因素对滑体稳定性的影响主要分为后缘张裂缝中静水压力对滑体的推力,以及通过滑移面上的静水压力减小滑移面抗剪强度两方面影响。当后缘张裂缝中充水高度大于临界水位高度时,滑体将发生失稳。
(3)对实例的分析表明滑移面上的静水压力相对于后缘张裂缝中的静水压力对滑体稳定性的影响更大,后缘充水高度的变化对稳定性系数影响幅度不大,治理该类滑坡时滑移面上的排水比后缘张裂缝中的排水更为重要。
[1]任光明,夏敏,李果,等.陡倾顺层岩质斜坡倾倒变形破坏特征研究[J].岩石力学与工程学报,2009,28(S1):3193-3200.
[2]谭儒蛟,杨旭朝,胡瑞林.反倾岩体边坡变形机制与稳定性评价研究综述[J].岩土力学,2009,30(2):479-482.
[3]李天扶.论层状岩石边坡的倾倒破坏[J].西北水电,2006(3):4-6.
[4]谭龙金,张海娜,盛韩微,等.水力作用下缓倾顺层岩质边坡滑移破坏机制分析[J].长江科学院院报,2014,31(9):47-52.
[5]陈全明.陡倾顺层岩质斜坡倾倒变形破坏机制的数值模拟研究[D].成都:成都理工大学,2011.
[6]张以晨,佴磊,沈世伟等.反倾层状岩质边坡倾倒破坏力学模型[J].吉林大学学报(自然科学版),2011,41(S1):207-213.
[7]舒继森,王兴中,周义勇.岩石边坡中滑动面水压分布假设的改进[J].中国矿业大学学报,2004,33(5):509-512.
Toppling Failure of Steeply Dipped Bedding Rock Slope under Hydraulic Actions
Lin Biting,Yuan Baoyuan,Zou Kai and Gui Yongqing
(School of Earth Science and Engineering,Hohai University,Nanjing,Jiangsu 211100)
The hydraulic actions are of vital importance to steeply dipped bedding rock slope deformation and failure.To think of steep⁃ly dipped bedding rock slope as a cantilever beam under dead-weight and hydraulic actions,established a mechanical model for the slope deformation and failure in different phases under hydraulic action and revealed the process.Through quantitative analyses of im⁃pacts from gliding plane hydrostatic pressure and water filling height in trailing edge tensional fractures,worked out slope stability coef⁃ficient and expression of critical water filling height.The result has shown that the toppling moment from hydraulic actions is the impor⁃tant reason of toppling deformation and failure of this kind slopes;the lowering down of slope stability coefficient is also caused by hy⁃draulic actions.Drainage is the primary measure to prevent and control toppling deformation and failure of this kind slopes.
steeply dipped bedding rock slope;hydraulic action;mechanical model;toppling failure;slope stability
P642.2
A
10.3969/j.issn.1674-1803.2016.12.10
1674-1803(2016)12-0055-07
林必挺(1991—),男,福建闽侯人,在读硕士研究生,研究方向:工程地质。
袁宝远(1967—),男,江苏海安人,教授、博士生导师。
2016-06-08
责任编辑:樊小舟

