基于铣削力仿真的稳定域叶瓣图构建*

李宏坤， 周 帅, 任远杰， 丛 明， 赵鹏仕

(1.大连理工大学机械工程学院 大连，116024)(2.大连新宇理工科技开发中心有限公司 大连，116024)



基于铣削力仿真的稳定域叶瓣图构建*

李宏坤1,2， 周 帅1,2, 任远杰1,2， 丛 明1,2， 赵鹏仕1,2

(1.大连理工大学机械工程学院 大连，116024)(2.大连新宇理工科技开发中心有限公司 大连，116024)

颤振稳定域分析的叶瓣图构建为铣削过程中参数优化的基础，但对于实际加工来说，铣削力不易通过测试获取。针对此问题，展开了基于铣削力仿真的叶瓣图构建方法研究。首先，通过有限元仿真模拟实际铣削过程，得到铣削力大小以及铣削力系数；其次，通过模态试验获取主轴-刀具系统的模态参数，再以铣削系数和模态参数为基础，构建铣削稳定性叶瓣图；最后，结合实际铣削加工的试验测试验证了叶瓣图的正确性。本研究可为优化切削参数、抑制实际铣削过程中颤振的产生提供参考，不仅可以提高工件的加工效率，也增强了系统的稳定性。

铣削力； 稳定性； 仿真模拟；参数优化

引 言

在机械加工行业中，铣削是最为常见的加工方式之一，切削过程中如果振动过大不仅会影响产品质量和精度，还会降低设备的稳定性和可靠性，严重时甚至带来人身安全问题。结合机床固有的特性，以及针对的刀具和加工材料，选择合适的加工参数是避开加工振动的有效措施。加工过程中的颤振稳定域分析为准确选择切削参数提供了参考和依据，得到了国内外许多学者的研究。

Cook[1]认为加工表面在后刀面的相对位移与切屑在前刀面的相对位移的耦合是造成颤振的主要原因。Albold[2]认为机床的阻尼大小与颤振有着紧密联系，加工过程中导致颤振的发生是因为阻尼小于零。Altintas等[3]完善了线性再生型颤振的理论方法，可应用于一般的精度加工系统。文献[4]提出了零阶解析法(zero-oder analytical，简称ZOA)求解颤振稳定性叶瓣图，作为选择稳定性切削所采用的切削参数理论依据。Tlusty等[5]提出了差分动态响应计算的方法来计算刀尖动态位移响应。Liu等[6]利用Runge-Kutta法，计算刀尖的动态响应变化，然后根据不同的判定准则鉴别其是否发生颤振。上述方法都是在时域进行求解，计算过程中为求精确需要不停地变化切深与转速，计算量较大。Insperger等[7]提出了半离散法计算方法，在一个周期内，将时滞项做离散后加权平均，将时滞微分方程变为常微分方程，然后计算其传递矩阵特征值的模,以此判断稳定性。

针对特定机床的主轴-刀具系统，要想得到主轴转速及相对应临界切深之间的关系，只需获取切削力系数、主轴-刀具系统的特征参数(固有频率、阻尼比及刚度)、颤振频率、刀齿数，由主轴转速及相对应临界切深作为坐标系x,y轴，这样就可以得到机床主轴-刀具系统的稳定性叶瓣图。系统的动态参数识别和铣削系数获取是基于ZOA颤振稳定域构建方法的关键问题。铣削系数需要通过测试铣削力才能得到，但在实际过程中，铣削力很难进行测试，这在很大程度上限制了基于稳定域构建的实际参数优化。为此，笔者从铣削力的仿真出发，通过仿真计算获取加工过程的铣削力，并以此获取铣削力系数，从而构建稳定域分析叶瓣图，指导实际过程的参数优化。

1 铣削力仿真

1.1 仿真理论基础

正交切削模型是一种应用广泛的二维铣削力模型。该模型是将动态变化的切削力分解为两个垂直正交方向上的瞬时圆周铣削力(切向力)和瞬时垂直切削力(径向力)，每一个方向的铣削力对应一个铣削力系数，同时切向力和径向力之间是线性关系。将二维模型增大到三维空间，模型的基本表达式为

(1)

其中：dFt为切向力微元；dFr为径向力微元；dFa为轴向力微元；ds为切削刃长度微元；dz为轴向切深微元；h为切削厚度；Ktc为切向力系数；Krc为径向力系数；Kac为轴向力系数；Kte为切向刃口力系数；Kre为径向刃口力系数；Kae为轴向刃口力系数。

将式(1)按照切削角度进行积分，可以推导出每齿周期平均切削力为

(2)

其中：ft=f/nN，为每齿进给量。

由式(2)可知，只要获得不同切削参数下的平均切削力，就能够识别出切削力系数。

工程材料在进行切削的过程中，切削层部分的材料都经过了大的塑性形变后才成为切屑。材料产生切屑分离时，必须满足材料屈服准则。笔者采用的屈服准则为Tresca准则[8]。

整个金属切削过程中，不仅要考虑应力的平衡方程，还要考虑边界条件。实际工程分析中，多采用上限原理[9]。为此，在材料本构方程方面采用的模型多为Johnson-Cook模型[10]。从刀具磨损因素出发，采用的是Usui磨损模型[11]。目前，计算切削热和切削力相互关系的方法有两种,增量区间有限元迭代法[12]和准静态迭代法[13]，笔者选择准静态迭代法。由于高温会使切屑材料、刀具和工件之间产生黏结现象[14]，黏结层附近还会产生正常摩擦挤压，其摩擦应力满足最基本的库仑定律。

笔者所用的有限元分析软件是DEFORM，该软件中包含多种材料成型与热处理数值模拟分析的模块，其分析结果包括了切削力变化分析、应力分布、刀具磨损预测及切削区域温度场分布等[15]。所用铣刀刀片的实际形状和几何模型如图1所示，刀片参数如表1所示。

图1 铣刀刀片Fig.1 Milling cutter

铣刀直径/mm几何尺寸/mm厚度/mm前角/(°)后角/(°)328×84．75515

1.2 铣削力仿真以及铣削力系数的获取

仿真工件材料为45#钢，铣刀材料为WC基质的硬质合金刀片。材料性能参数如表2所示。工件-刀具接触参数如表3所示。

表2 刀具与工件热力学参数

Tab.2 Heat-dynamics parameters for cutter and work-piece

物理参数工件(45#钢)刀具(WC)弹性模量/MPaE(T)600泊松比ν0．30．22热导率/(W·m-1·℃-1)k(T)120比热容/(J·kg-1·℃-1)c(T)222热系数/(m·m-1·℃-1)α(T)5×10-6塑性转化系数0．9—熔化温度/℃1500—初始环境温度/℃2020硬度HRC3055密度/(kg·m-3)786014900

表3 工件-刀具接触参数

图2所示为有限元铣削模拟仿真第30步与第1 740步的模拟铣削状况。

图2 铣削过程的模拟仿真Fig.2 Simulation of milling process

图3所示为按照试验切削参数进行的铣削模拟仿真切削力的大小，其中的尖峰值是由于网格划分而引起的噪声信号。利用小波分解并重构[16]，去除尖峰值得到平稳的铣削力，如图4所示。

图3 切削力仿真信号Fig.3 Simulation signal for milling force

图4 处理后的切削力仿真信号Fgi.4 Pre-processing milling force signal

通过仿真得到不同切削参数下的切削力曲线，获取平均铣削力，根据式(2)计算铣削力系数，如表4所示。

表4 铣削力系数

2 主轴-刀具系统参数识别

模态试验是通过振动测试来确定系统的固有频率、阻尼比、刚度和模态振型，是一种用来分析机构动力学特性的方法,测试装置示意图如图5所示。

图5 模态试验的测试装置示意图Fig.5 Schematic diagram for modal experiment

模态试验在大连理工大学模具所的东昱精机CMV-850A加工中心进行。所用刀具直径为32 mm，为英国斯特拉姆(ATI stellram)公司生产的7792VXD型镶片牛鼻铣刀(刀片型号为ATI stellram-X500)，刀片数为3。模态试验设备如下：PCB冲击力锤，灵敏度为2.25 mV/N；PCB加速度传感器，灵敏度为93 mV/g；NI USB-9234型4通道数据采集卡；北京东方振动与噪声技术研究所Coinv DASP V10多通道信号采集和实时分析软件。为了提高模态测试精度，采用三次锤击激励然后求取平均值。图6所示为试验所获得的x，y方向的刀具频响函数曲线。

图6 刀具频响函数曲线Fig.6 The curve of milling cutter frequency response function

在获得刀具频响函数曲线之后，利用东方所DASP模态分析软件自带的PolyLSCF频响曲线处理算法，经过分析处理，便可获得刀具x，y方向上的模态参数，如表5所示。

表5 刀具系统模态参数

3 颤振稳定域建模

结合试验所获得刀具系统模态参数及铣削力系数，利用Matlab编程计算，根据式(3)便可绘制铣削颤振稳定域叶瓣图(见图7)。

(3)

其中：k为叶瓣数；aplim为临界切深；N为刀齿数；n为主轴转速；Kt为铣削力系数；ΛR与ΛI分别机床主轴系统传递函数特征方程根的实部与虚部；ωc为颤振频率。

图7 45#钢铣削稳定性叶瓣图Fig.7 Milling stability lobe of steel 45#

由图7可以看出，选择曲线下方的切削参数进行加工为稳定加工区域，其中选择虚线以下部分的切削参数为绝对稳定区，选择曲线以上部分的切削参数进行切削为容易发生颤振的区域。根据叶瓣图选取合理的加工参数可以避免颤振，能获得比较高的加工效率、良好的加工表面及精度，保护机床与刀具。图7中在主轴转速为600～1 000 r/min之间有较大的稳定区域，在制定切削参数时优先在该区域选取，并尽量避免靠近叶瓣图曲线。

4 试验验证

根据绘制的叶瓣图，选择A，B，C点不同的切削参数进行验证，如图8所示，3点的切削参数如表6所示。目前，通过对所采集的力信号做FFT变换，观察其时域信号及频域信号的特征，便可判断是否发生颤振[17]。

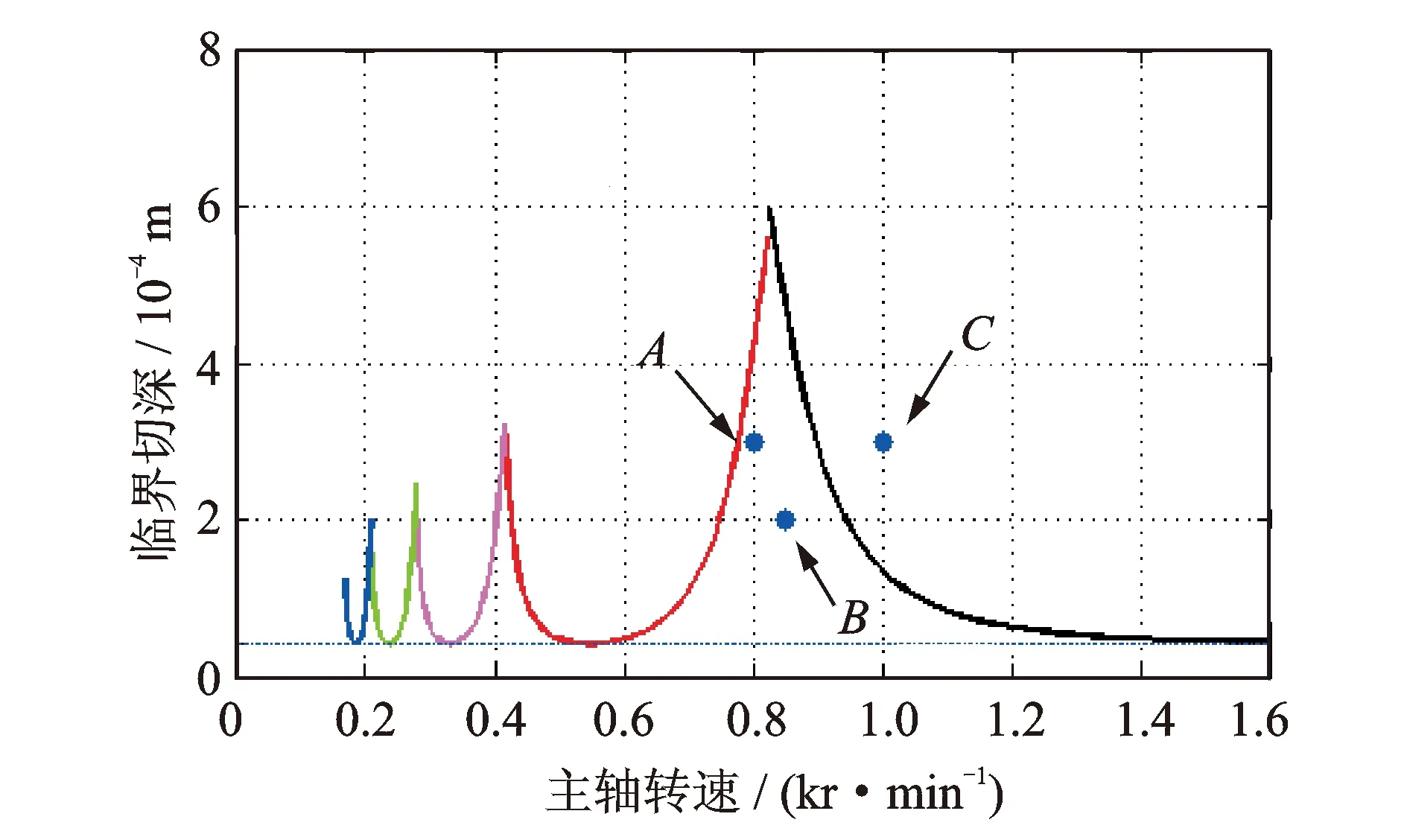
图8 叶瓣图中验证点的选取Fig.8 Different verification point in the stability lobe

点号主轴转速/(r·min-1)切深/mm进给速度/(mm·mm-1)预判A8000．3200稳定B8500．2200稳定C10000．3200不稳定

A，B，C点的时域信号与频域信号如图9～图14所示。

图9 A点铣削力的时域信号Fig.9 Time domain milling force signal of A point

图10 A点铣削力的频域信号Fig.10 Frequency domain milling force signal of A point

A点的时域信号平稳可靠，其主轴转速为800 r/min，刀齿数N=3，对应轴频率为13.4 Hz，所以切削频率为39.8 Hz(13.4 Hz×3)。在图10中所显示的频率为主轴的旋转频率以及倍频，没有出现颤振频率。

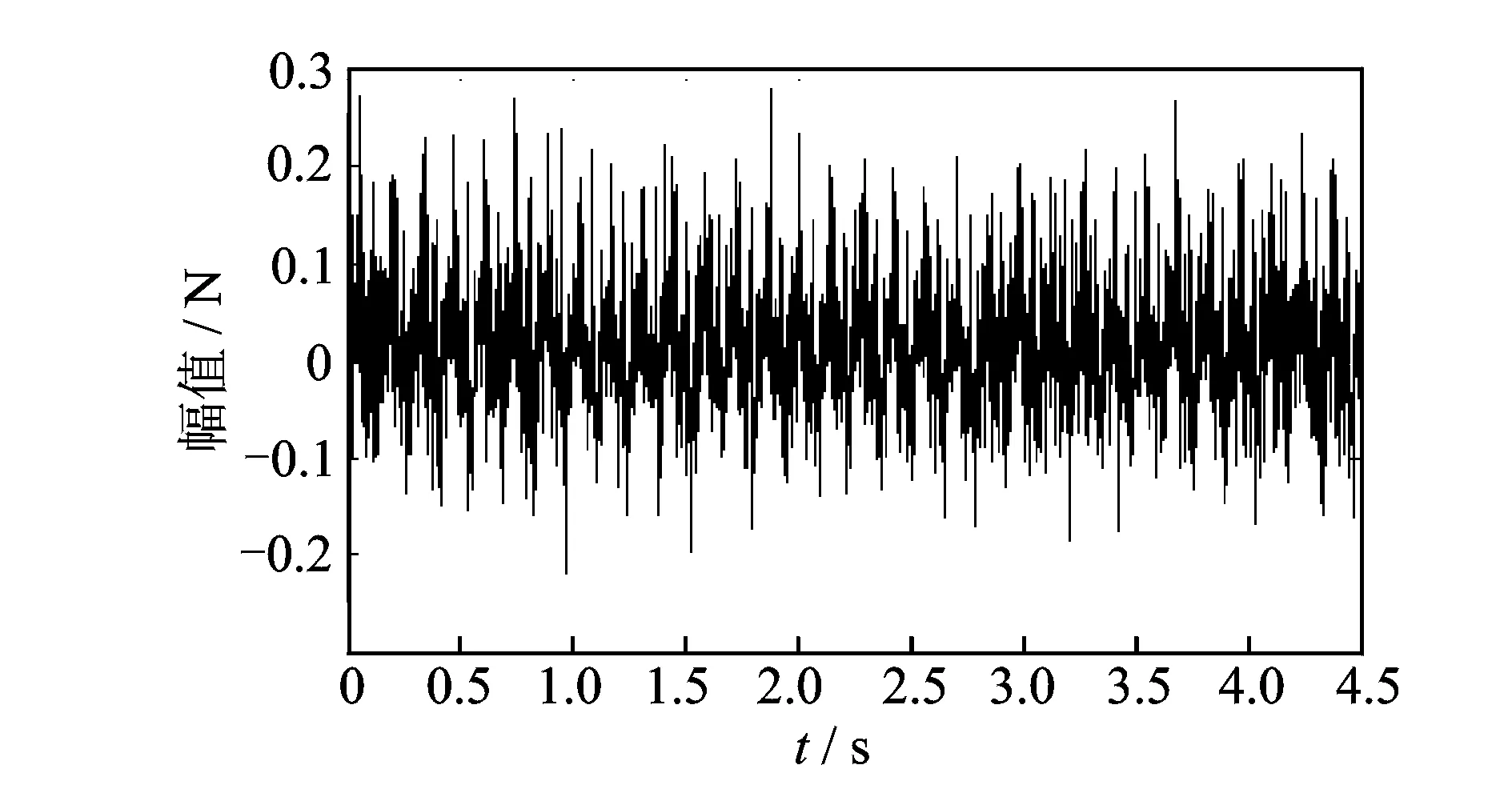
图11 B点铣削力的时域信号Fig.11 Time domain milling force signal of B point

图12 B点铣削力的时域信号Fig.12 Frequency domain milling force signal of B point

图13 C点铣削力的时域信号Fig.13 Time domain milling force signal of C point

图14 C点铣削力的频域信号Fig.14 Frequency domain milling force signal of C point

B点时域信号主轴转速为850 r/min，旋转频率为14.2 Hz，所以切削频率为42.6 Hz(14.2 Hz×3)。与A点的结论一样，图中出现都是与主轴旋转频率相关的倍频，并没有出现颤振频率，所以判定B点是一个稳定切削点。

观察C点时域信号，其幅值明显增大，但不能判断是否发生颤振。在频域信号中，其主轴转速为1 kr/min，主轴旋转频率为16.6 Hz，切削频率为49.8 Hz(16.6 Hz×3)。频谱图中除了转频外出现了频率249.2 Hz，此频率与表5中所示的刀具系统1阶固有频率非常接近，容易产生共振，可以判断C点是一个不稳定点。

综合时域信号与频谱图可以判定,以A，B点切削参数切削时，频域信号中都是转频及其倍频占主要成分，铣削过程是稳定切削；以C点切削参数切削时，除了转频外，出现了颤振频率，为不稳定切削。再反观叶瓣图，点A，B处在稳定切削区域，点C处在颤振区域。二者的结论相符合，证明了所构建的铣削稳定性叶瓣图正确可靠。

5 结束语

通过模拟仿真铣削过程，分析处理铣削力大小变化，结合铣削力模型的建立分析计算得到铣削力系数，以此为基础建立了稳定域分析的叶瓣图。结合试验对叶瓣图的可靠性进行验证，结果表明了此方法的正确性，为铣削参数的优化提供了理论支持和依据，缩短了试验进行参数选择所需的时间。

[1] Cook N H. Self-excited vibrations in metal cutting[J]. Journal of Engineering for Industy-Ttansaction of the ASME， 1959,81:183-186.

[2] Arnold L. The mechanism of tool vibration in the cutting of steel[J]. Proceedings of the Institution of Mechanical Engineers, 1945,154:261-276.

[3] Altintas Y, Shamoto E, Lee P, et al. Analytical prediction of stability lobes in ball end milling [J]. Trans. ASME Journal of Manufacturing Science and Engineering， 1999,121(4):586-592.

[4] Altintas Y, Budak E. Analytical prediction of stability lobes in milling [J].CIRP Annals-Manufacturing Technology,1995,44(l):357-362.

[5] Tlusty J, Ismail F. Basic non-linearity in machining chatter[J]. CIRP Ann-Manuf Techn, 1981,30:299-304.

[6] Li Zhongqun, Liu Qiang. Solution and analysis of chatter stability for end milling in the time-domain[J]. Chinese Journal of Aeronautics, 2008,21(2):169-178.

[7] Insperger T, Stépán G. Semi-discretization method for delayed systems[J]. International Journal for Numerical Methods in Engineering, 2002,55(5):503-518.

[8] Tresca M H. On further applications of the flow of solids [J]. Journal of the Franklin Institute, 1878,106(6):396-404.

[9] Slater R A C. Engineering plasticity: theory and application to metal forming processes[M]. London and Basingstoke: Macmillan, 1977:50-57.

[10]Klocke F, Raedt H W, Hoppe S. 2D-FEM simulation of the orthogonal high speed cutting process[J]. Machining Science and Technology: An International Journal, 2001,5(3):232-340.

[11]Usui E, Obikawa T, Shirakashi T. Study on chipegmentation in machining titanium alloy[C]∥Proceedings of the 511′ International Conference on Production Engineering． Tokyo:[s.n.], 1984:223-239.

[12]Rebelo N, Kobayashi S. A coupled analysis of viscoplastic deformation and heat transfer-I: theoretical considerations [J]. International Journal of Mechanical Sciences, 1980,22(11):699-705.

[13]蔡旺．叶片精锻过程三维热力耦合有限元模拟[D]．西安：西北工业大学，2002.

[14]吴金炎, 王庆明.基于热力耦合模型的金属切削过程有限元分析[J].设计与硏究, 2009,36(2):18-21.

Wu Jinyan, Wang Qingming. Finite element analysis of metal orthogonal cutting process based on coupled thermo-mechanical model[J]. Journal of Machine Design and Research, 2009,36(2):18-21. (in Chinese)

[15]宋健.基于DEFORM-3D的发动机缸体钻削仿真及切削参数优化[D].大连:大连理工大学,2012.

[16]张臣国. 小波分析在信号降噪中的应用研究[D].成都:电子科技大学, 2012.

[17]Smith S, Tlusty J. Update on high-speed milling dynamics[J]. Journal of Engineering for Industry, 1990,112(2):142-149.

10.16450/j.cnki.issn.1004-6801.2016.06.016

*国家数控机床重大专项资助项目(2013ZX04012071)

2014-10-22；

2015-01-24

TH113.1

李宏坤, 男,1974年9月生，教授、博士生导师。主要研究方向为机械设备故障诊断、振动抑制及可靠性评估研究。曾发表《基于KPCA-SCM的柴油机状态识别研究》(《振动、测试与诊断》2009年第29卷第1期)等论文。 E-mail:lihk@dlut.edu.cn