面向压电泵脉动消除的流体滤波器设计与实验*

吴 宣， 陈立国， 贺文元， 潘明强

(1.苏州大学机器人与微系统研究中心 苏州，215021) (2.苏州纳米科技协同创新中心 苏州，215021)



面向压电泵脉动消除的流体滤波器设计与实验*

吴 宣1,2， 陈立国1,2， 贺文元1,2， 潘明强1,2

(1.苏州大学机器人与微系统研究中心 苏州，215021) (2.苏州纳米科技协同创新中心 苏州，215021)

设计了一种被动式流体滤波器，它由薄膜及微通道组成，旨在消除由压电泵引起的流体脉动。对流体滤波器进行了理论分析，利用Comsol软件建立滤波器的有限元模型，分别对薄膜变形以及微通道流阻进行数值计算，并分析了影响滤波效果的参数。仿真结果表明，当微通道内的流体阻力较大时，泵的驱动频率越高，薄膜半径越大，滤波效果更佳。通过实验验证，表明所设计的流体滤波器可以有效减小脉动，压电泵能够提供稳定的流量。

流体滤波器； 流体脉动； 微流量； 压电泵

引 言

近年来，许多非机械泵被用来驱动微流动系统，其驱动原理是电流体驱动[1]、电磁制动[2]和电渗[3]等，这类泵需要将电场、磁场等直接作用在流体之上，因此它们只能输送特定组分的溶液，应用范围相对狭隘。压电泵具有结构简单、体积小、重量轻、驱动力大、低泄漏、响应时间短、耗能低、无噪声和无电磁干扰等优点[4-5]，并且其特有的驱动原理决定了其拥有更广阔的发展前景。但是，压电泵输送的流量是脉动的，会对流体操作的快速性、稳定性和精确性产生不利影响，因而需要抑制压电泵的脉动。

国内外学者分别从不同的角度展开了对压电泵脉动消除的研究，主要可分为压电泵的结构和流体传输过程两个方面。结构方面，从压电泵的主要构成部分，即振子、阀及流道3个方面进行了研究。从最初的单腔单振子压电泵到多腔体多振子结构，从有阀压电泵到无阀结构[6-7]等优化措施明显减弱了工作时的脉动现象，并且大大提高了输出性能。流体运输方面，Yang等[8]提出了一种稳定器结构用于稳定流体的波动，Inman等[9]在主动阀气动泵出口加入了由薄膜以及fluidic resistor组成的滤波单元。笔者设计了一种面向压电泵脉动消除的被动式流体滤波器，并通过实验验证了流体滤波器的滤波效果。

1 流体滤波器结构设计

在液压系统中常采用亥姆霍兹原理来削减液压管路中的脉动以达到消声的效果，但是由于压电泵泵送流体的压力较低且频率在0～150 Hz范围内，难以依靠共振导致的摩擦来吸收能量。所以，笔者采用PDMS薄膜与微通道的组合构成被动式流体滤波器，对压电泵的脉动流体进行滤波。

笔者设计的流体滤波器结构，如图1所示，它由玻璃基板、PDMS薄膜和微流道组成。薄膜夹在两层玻璃板之间，在上玻璃板上刻蚀出微通道，在下玻璃板上钻孔使薄膜能在开孔处扩张收缩。

图1 流体滤波器结构示意图Fig.1 Schematic of the stabilizer

压电泵输出的脉动流体从左侧进口流入，当进口流速大于出口流速时，如图2(a)所示，薄膜向下扩张，将流体储存在由薄膜形成的容腔中，容腔内流体压力也随之增大；当进口流速低于出口流速时，见图2(b)，薄膜向上收缩，泵出容腔内的流体，容腔内压力减小，使得出口流速在较小的范围内波动。

图2 流体稳定器工作原理示意图Fig.2 Operating principle of the stabilizer

2 流体滤波器建模

根据前文设计的流体滤波器的结构，对各组成部分进行建模与分析。

2.1 PDMS薄膜变形分析

PDMS是一种无色透明的弹性高分子聚合物，具有良好的生物兼容性，因此被广泛应用在各种微流控分析系统中。

流体滤波器的工作过程中，当流体进入时，在下层玻璃圆孔处的PDMS薄膜由于受到来自进口流体的压力p发生轴向变形，变形情况如图3所示。薄膜变形挠度用w表示，由于薄膜被键合在玻璃之上，薄膜的受力状态可用夹支圆形薄板近似表示。

图3 均匀压力p下的变形示意图Fig.3 Member deformed by the pressure p

当压力均匀分布的时候，膜的变形量[10]可由式(1)得到

(1)

其中:a为膜的半径；r为距离中心点的距离；D为抗弯刚度。

(2)

其中:E为弹性模量；h为膜的厚度；u为泊松比。

用V代表薄膜变形引起的体积变化量，如图4所示。

图4 薄膜变形体积示意图Fig.4 The volume of the capacitor

薄膜沿中心轴轴对称，度曲线沿对称轴旋转并对r积分，可得薄膜变形形成的容腔体积V

(3)

(4)

由式(5)可知，薄膜与玻璃形成的容腔体积V与薄膜上的压力p成正比，并且与薄膜的半径a、薄膜的弹性模量E以及泊松比u相关，因此在设计结构时需考虑这3个参数的影响。PDMS薄膜的泊松比u约为0.49[11]。然而PDMS的弹性模量与前驱物的比例有关，不同比例所得到的弹性模量参数如表1所示。笔者使用1∶10的比例来制作PDMS，得到弹性模量为750 kPa的PDMS薄膜。

表1 PDMS材料配比与弹性模量的关系

2.2 微通道建模

流体流经细小管路，管路两端压力损失与液体流经管路时的速度有关。由于管径细小，流体一般做层流运动，管路两端压力差和流速关系[12]为

(5)

其中：Δp为通道两端的压力差;Qout为流速;C为无纲量摩擦因数;μ为流体的黏性系数;L为通道的长度;A为管路的截面积;Dh为管路的水力直径(有效截面积与湿周之比的4倍)。

式(5)反映出微通道两端的压力差与通道的长度成正比，与通道的截面积成反比。

定义通道的流阻R为通道两端压差与流经通道的流量的比值，R可表示为

(6)

2.3 流体滤波器工作建模

容腔内体积V为进口流量Vin与出口流量Vout之差，即

(7)

其中:Qin为进口流量;Qout为出口流量。

p=kV表示了腔体体积和压力之间的关系。体积V可由式(8)给出

(8)

利用Matlab软件中的Simulink模块搭建了滤波模型，如图5所示。

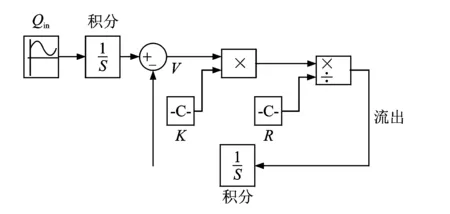
图5 Simulink滤波模型Fig.5 Simulink filter model

通常，在分析滤波器性能时，用进口流量的波动幅值ΔQin与出口流量波动的幅值ΔQout的比值来评价滤波器的稳定率Rf

(9)

图6 Simulink建模分析计算结果Fig.6 Resultes of analysis and modeling of the Simulink model

依据该模型对流体滤波器进行分析，Simulink计算结果见图6。其中：图6(a)为正弦形式的进口流量曲线；图6(b)为对应的出口流量曲线；图6(c)为薄膜容腔中的液体体积；图6(d)为微通道两端的压力差。从图6 (b)可以看出，出口流量在开始阶段有一个缓慢上升的过程，这是由于开始阶段PDMS薄膜还处于初始状态没有发生变形。当进口有流体持续流入后，薄膜上的压力增大，薄膜向下扩张，容腔体积不断增大。随着容腔内压力增大，从微通道流过的液体流速也不断增加。

3 流体滤波器有限元建模分析

笔者利用Comsol软件对流体滤波器进行有限元分析。

流体滤波器工作时，进口处正弦脉动流的流量由恒定的平均流量和薄膜形变产生的容腔体积组成，可根据式(10)得到

(10)

当流体滤波器工作时，流体的压力和膜会发生相应的形变，其情况见图7。研究过程中各项参数如下：流体的黏性系数u=0.001 003 kg/(m·s);流体密度ρ=998.2 kg/m3;室温T=20℃;出口的压力为p=0。

对流体滤波器的工作过程进行仿真，模拟仿真时，出口流量值与进口流量值的对比如图8所示。

图8 进口与出口流量对比图Fig.8 Simulated time courses of flow rates

分析图8，可以得到如下的数据：进口处的平均流量Qavg=0，流量波动的振幅ΔQavg=210 uL/min;频率f=10 Hz。大约10个周期后，出口流量达到稳定状态。由图可以看出，出口流量曲线与容腔内的压力曲线相似，经过滤波器滤波之后，出口流量的波动幅值仅为进口流量波动幅值的1/20，即滤波器的稳定率Rf=20，这表明流体滤波器性能良好。

通过前面理论推导，分析得出影响滤波效果的因素主要有通道流阻、驱动电压频率和薄膜半径(即PDMS薄膜与玻璃板圆孔之间形成的腔体的半径)。

不同通道流阻对滤波的影响分析如下：为了研究通道流阻对滤波效果的影响，仿真时采用相同尺寸的薄膜、不同尺寸的微通道，使通道流阻分别为1～9 (Pa·s)/m3，平稳后稳定器进出口的波动比如图9所示。

图9 不同通道流阻的影响 图10 平稳的周期数 Fig.9 Influence of the Fig.10 Influence on fluidic resistance cycles reaching steady

从图9、图10可以看出,随着通道流阻从10～55的增大，进出口波动比也随之增大，呈线性关系。虽然如图所示选取大的通道流阻可以获得更好的滤波效果，但式(6)也反映出大的通道流阻会导致较大的压力损失。同时图10也反映出通道流阻增大时出口流体达到稳定需要更长的周期。

图11 不同频率的影响图12 不同薄膜半径的影响 Fig.11 Influence of the Fig.12 Influence of the pump frequency capacitor′s radius

不同频率对滤波效果的影响分析如下：在控制其他参数相同的情况下，升高频率，结果如图11所示，进出口的波动比也随之增加。由图可以观察到，当进口的驱动频率大于10 Hz时，进出口波动比就已经大于50。因此，在对流体滤波器的设计过程中，可以选用相对较高的压电泵驱动频率来获得好的滤波效果。

薄膜半径对滤波效果的影响如下：仿真时固定薄膜的厚度和通道流阻等参数，选取半径为2，3，4，5，6 mm的薄膜，结果如图12所示。

由图12可以看出，增大薄膜的半径可以显著提高滤波效果。当薄膜半径达到5mm时，出口波动幅值仅为进口波动幅值的1%。

综合上述三方面的分析结果，发现在对流体滤波器的设计过程中，增大薄膜的半径，升高压电泵驱动电压的频率和增大微通道的流阻都可以实现流体滤波器性能的优化。采取增大微通道流阻方法需要十分谨慎，因为该方法虽然能使性能更好，但是也会相应的增加微流体系统的准备时间。

4 实 验

基于前面对流体滤波器的分析与设计，加工出流体滤波器装置，其固定的参数如下：PDMS薄膜的弹性模量为750kPa，微通道的宽度为200 μm，深度为50 μm。将其加入到压电泵的输出口，利用流量传感器分析比较加入流体滤波器的滤波效果。

选用方波作为压电泵的驱动电压，利用流量传感器检测未加入流体滤波器时压电泵的输出流量值，不同电压频率的情况下，压电泵出口流量如图13所示。

图13 不同频率时的出口流量Fig.13 Influence of the pump frequency

在压电泵与流量传感器之间引入笔者设计的滤波器，得到的流量图如图14所示。

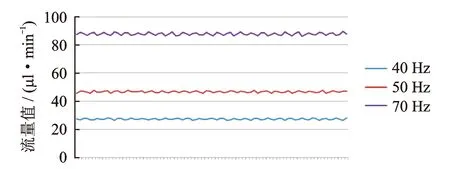
图14 加滤波器不同频率下的出口流量Fig.14 Influence of the pump frequency with the stabilizer

分析以上的出口流量值，总结得出表2和表3中的数据。对表2和表3进行分析比较得知：未加入流体滤波器时，随着压电泵驱动频率的升高，出口处的流量脉动幅值越大，最大波动值相对于平均流量值的比值也随之增大，脉动现象越明显；加入流体滤波器后，最大波动值与平均流量值的比值随着驱动频率的升高而减小。因此，选择较高的驱动频率，可以得到更好的滤波效果，与仿真结果一致。

保证其余各参数保持一致，分别在压电泵和流量传感器之间加入笔者设计的两种不同长度微通道的流量滤波器，微通道的长度分别为18和23 μm，出口流量图与未加入流体滤波器出口流量值对比如图15所示。

表2 不同频率下的出口流量

Tab.2 Influence of the pump frequency

f/Hz平均流量值μl/min最大波动值μl/min比值/%40165．826828．828217．3850277．437654．989619．8270525．7582125．448023．86

表3 加入流体滤波器后不同频率下的出口流量

图15 不同流阻下的出口流量Fig.15 Influence of the fluidic resistance

图16 加滤波器不同流阻下的出口流量Fig.16 Influence of the fluidic resistance with the stabilizer

放大加入流体滤波器后两组出口流量值区域的图,如图16所示。当压电泵驱动频率相同时取不同的驱动电压幅值，比较不同驱动电压幅值时，加入两流体滤波器后最大脉动与平均值的比值，如表4所示(采用百分制)。

分析表4中的数据，比较两种流阻的流体滤波器的滤波效果可以发现，随着微通道长度的增长，即随着流阻的增大，最大脉动值与平均流量值的比值也相应减小，流体滤波器的滤波效果越好，与仿真结果一致。

表4 不同长度微通道滤波效果对比

保证其余各参数保持一致，分别在压电泵和流量传感器之间加入笔者设计的两种不同薄膜半径的流量传感器，同频率下电压幅值从110V变化到120V时出口流量值对比如图17所示。

图17 不同薄膜半径下的出口流量Fig.17 Influence of the capacitor′s radius

分析两个不同半径的流体滤波器对滤波效果的影响，由图17可以看出，流体流经薄膜半径为8 μm的流体滤波器时最大波动值相对较小，即薄膜半径越大时流体滤波器的整体滤波效果越佳。

5 结束语

笔者分析和设计了一种被动式流体滤波器，该装置利用PDMS薄膜和微通道来消除压电泵输出的脉动流体的波动。研究结果表明，当微通道内的流体阻力较大时，泵的驱动频率越高，薄膜半径越大，流体滤波器滤波效果更佳。通过实验验证，结果表明所设计的流体滤波器对压电泵的脉动有很好的效果。本流体滤波器可以应用到细胞操纵、药物输送和微透析等需要稳定流量的领域中，并且流体滤波器可以根据相应的需求流量值进行不同程度的优化，因此该流体滤波器具有更加广阔的发展前景。

[1] Bart S F, Tavrow L S, Mehregany M, et al. Microfabricated electrohydrodynamic pumps[J]. Sensors Actuators, 1990,21:193-197.

[2] Jang J, Lee S S. Theoretical and experimental study of mhd (magnetohydrodynamic) micropump[J]. Sensors Actuators, 2000,80:84-89.

[3] Manz A, Effenhauser C S, Burggraf N, et al. Electroosmotic pumping and electrophoretic separations for miniaturized chemical analysis systems[J]. Microeng, 1994,4:257-265.

[4] 何秀华,张睿,蒋权英.基于MEMS的压电泵及其研究进展[J].排灌机械,2007, 25(4):64-68.

He Xiuhua, Zhang Rui, Jiang Quanying. Progress on piezoelectric micropump based on MEMS[J]. Drainage and Irrigation Machinery, 2007, 25(4):64-68. (in Chinese)

[5] 阚君武,杨志刚,程光明.压电泵的现状与发展[J].光学精密工程，2002, 10(6):619-625.

Han Junwu, Yang Zhigang, Cheng Guangming. Re-

search on piezoelectric pump and its development[J]. Optics and Precision Engineering, 2002, 10(6):619-625. (in Chinese)

[6] 吴丽萍. 扁锥腔无阀压电泵理论与实验研究[D]. 长春: 吉林大学, 2008.

[7] 谢海峰. 压电共振型隔膜泵的设计理论与试验研究[D]. 长春： 吉林大学, 2013.

[8] Yang B Z, Lin Q. A compliance-based microflow stabilizer[J]. Journal of Microelectromechanical Systems, 2009,18:539-546.

[9] Inman W, Domansky K. Design, modeling and fabrication of a constant flow pneumatic micropump[J]. Journal of Microelectromechanical Systems, 2007,17:891-899.

[10]Timoshenko S P. Theory of plates and shells[M]. 2nd. New York: McGraw-Hill, 1959:124-130.

[11]Cui H H. Preparation and performance analysis of a pdms membrane microvalve[J]. Microfabrication Techonlogy, 2004,3:70-75.

[12]White F M. FluidMechanics[M]. 5th ed. New York: McGraw-Hill, 2002:60-80.

10.16450/j.cnki.issn.1004-6801.2016.06.014

*国家高技术研究发展计划(“八六三”计划)资助项目(2011AA040404)；高等学校博士学科点专项科研基金资助项目(20133201110009)；新世纪优秀人才支持计划资助项目(NCET-13-0923)

2014-12-24；

2015-03-11

TH113.2; TH162；TN389

吴宣,女，1990年12月生，硕士生。主要研究方向为微流控。E-mail: wuxuan_wendy@126.com