考虑谐波因素的配电网无功补偿配置优化方法
陈晓春 王曜飞 宋亚夫 王立娜 刘 杨 张占龙 旦乙画
(1. 浙江缙云县供电公司, 浙江 缙云 321400;2. 重庆大学输配电装备及系统安全与新技术国家重点实验室, 重庆 400044)
考虑谐波因素的配电网无功补偿配置优化方法
陈晓春1王曜飞1宋亚夫1王立娜1刘 杨1张占龙2旦乙画2
(1. 浙江缙云县供电公司, 浙江 缙云 321400;2. 重庆大学输配电装备及系统安全与新技术国家重点实验室, 重庆 400044)
针对谐波污染影响配电网无功补偿配置优化的特点,建立考虑谐波因素的配电网无功补偿配置优化简化模型。对各节点的电压有效值和电压总谐波畸变率进行约束,在保证目标函数最小的同时,将各节点的电压有效值和电压总谐波畸变率控制在允许范围之内。针对粒子群算法用于无功补偿优化时存在的局部最优收敛问题,作了算法改进,并将其应用于简化模型求解。选取了IEEE11节点配电网和实际配电网进行优化计算,结果验证了该算法改善电压水平、抑制谐波及降低配电网有功网损等作用的有效性。
谐波; 配电网; 无功补偿; 粒子群算法
进行无功补偿是改善配电网电压质量和降损节能的有效手段之一。随着电力电子技术的发展,非线性设备在配电网中的应用越来越广泛,而其伴生的配电网谐波污染也日趋严重。谐波对配电网的危害极大,严重影响配电网中的电气设备及无功补偿装置的经济可靠运行[1]。已有文献提出了考虑谐波因素的配电网无功补偿配置优化模型,以配电网有功网损费用和电容器投资费用之和最小为目标函数[2]。但此项研究中仅考虑了单一的负荷水平,且将根节点的谐波电压视为唯一的谐波源。配电网无功补偿配置优化问题是一个非线性函数优化问题,而目前基于数学规划法的经典无功优化算法通常比较繁琐。人工智能优化算法为求解该问题提供了新思路,因此需要对算法进行不断改进从而彻底解决配电网无功补偿配置优化问题[3]。
粒子群优化算法(Particle Swarm Optimization, 缩写为PSO)是一种基于群体智能的优化算法。该算法在函数优化、模式识别、神经网络训练、电力系统优化等方面应用广泛。PSO算法用于配电网无功补偿配置优化问题求解,具有原理简单、容易实现、易于与其他算法融合等优点,但同时存在容易陷入局部最优的收敛问题。有研究者提出了基于模糊系统的惯性权重调整策略[4],但未考虑到通过加速因子进行调节。
本次研究中,根据配电网的实际情况,建立了考虑谐波因素的配电网无功补偿配置优化简化模型。以配电网有功网损和电容器投资费用最小为目标函数,以系统潮流约束、控制变量约束和状态变量约束为约束条件,在保证目标函数最小的前提下,有效地将配电网各节点的电压水平和总谐波畸变率控制在允许范围之内。
1 考虑谐波因素的配电网无功补偿配置优化模型
1.1 目标函数
考虑谐波因素的配电网无功补偿配置优化模型中,以配电网有功网损和电容器投资费用最小为目标函数,综合这2项指标对优化配置方案进行评价。目标函数(F(x))见式(1):
min(F(x))=min(F1,F2)
(1)
式中:F1为配电网有功网损;F2为配电网电容器投资费用。
1.1.1 配电网有功网损
由于配电网负荷分布不均,若是只对一种负荷水平进行研究,不免具有片面性。在此,设配电网负荷由最大负荷水平、一般负荷水平和最小负荷水平组成,既避免了片面性,也能使模型更真实地模拟配电网的实际运行状态。
在负荷水平i下各节点的有功网损表示为Ploss(i),有功功率和无功功率分别表示为P(i)和Q(i),对应的节点电压和电阻分别为U(i)和R,假设各节点的电容器安装容量为Q0,则补偿后负荷水平i下各节点的网损Ploss(i)由式(2)计算:
(2)
考虑谐波因素时,在负荷水平下配电网的有功网损为基波有功网损和各次谐波有功网损的总和:
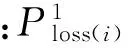
(3)
1.1.2 电容器投资费用
不同负荷水平下所补偿的容量有所不同,因此,无功补偿针对了固定电容器和可投切电容器2种不同的电容器。由于在现实生活中电容器通常是成组安装的,各补偿点的安装容量是单组标准容量的整数倍,所以电容器的投资费用是电容器的组数与单价的乘积。补偿节点j处的电容器投资费用为:
(4)
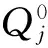
于是电容器的投资费用F2可以表示为:
(5)
1.2 系统潮流约束
1.2.1 基波潮流方程
基波潮流方程如式(6)所示[5]:
Gi(Xi,Qi)=0, i=1,2,3
(6)
式中:Xi、Qi分别表示负荷水平i下的状态变量向量和控制变量向量。
1.2.2 谐波潮流方程
谐波潮流方程如式(7)所示:
(7)
i=1,2,3;k=3,5,…,h
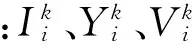
根据谐波电流约等于基波电流与谐波次数之比的近似关系,估算各节点的谐波注入电流,如式(8)所示:
(8)
i=1,2,3;k=3,5,…,h
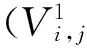
1.3 控制变量约束
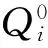
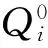
(9)
当补偿节点j处采用部分或全部的可投切电容器时,则在不同的负荷水平下电容器可能有不同的投入容量,即存在式(10)所示关系式:
(10)
1.4 状态变量约束

(11)
(12)

为了将各个节点的电压水平和电压总谐波畸变率控制在规定范围之内,需要对各节点电压的上下限以及THD的上限进行约束,如式(13)所示:
(13)
目标函数式(3)、(5)和约束条件式(6)、(7)、(10)、(13)构成了考虑谐波因素的配电网无功补偿配置的优化模型。
2 基于改进粒子群算法的求解方法
运用PSO算法,首先在可行解的空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解,粒子的特征由位置、速度和适应度这3项指标表示。其中,适应度通过适应度函数计算得到,其值反映粒子的优劣。粒子在可行解的空间中运动,通过跟踪个体极值Pbest和群体极值Gbest对粒子的位置进行更新。根据式(14)对粒子的速度和位置进行更新:
(14)
式中:Vid为粒子的速度;Xid为粒子的位置;ω为惯性权重;k为当前迭代次数;i=1,2,…,n;d=1,2,…,D;c1,c2为加速因子;r1,r2为分布于区间[0,1]的随机数。
2.1 关键参数设置的改进
2.1.1 惯性权重ω
惯性权重ω过大或过小都会影响算法的搜索结果,设置合理的惯性权重ω可以有效地提高算法的收敛性能。将惯性权重由最大值线性递减至最小值,迭代初期较大的惯性权重使算法保持了较强的全局搜索能力,而迭代后期较小的惯性权重有利于算法进行精确的局部搜索。于是改进后的惯性权重ω如式(15)所示:
ω(k)=ωstart-k(ωstart-ωend)Tmax
(15)
式中:ωstart为初始惯性权重;ωend为迭代至最大次数时的惯性权重;k为当前迭代次数;Tmax为最大迭代次数。
2.1.2 加速因子c1、c2
标准PSO算法的加速因子c1、c2控制着粒子的状态。选择恰当的加速因子可以提高算法的速度,避免陷入局部极小。在迭代初期,粒子具有丰富的多样性,相互作用力增加,此时可以让粒子多向其同伴学习;在迭代后期,粒子逐渐靠近最优解,此时可以适当增加其自身认知力,使粒子尽快收敛于最优解。加速因子c1、c2通过式(16)来计算:
(16)
随着迭代次数的增加,加速因子c1取值线性递增,其自身影响力也随之增大;而加速因子c2取值线性递减,其社会影响力随之减小。这样,既考虑了算法初期较强的全局搜索能力,又兼顾了算法后期侧重于精确度的局部搜索。
改进后的PSO算法如(17)所示:
(17)
2.2 控制变量的处理
对于有N个负荷节点数的配电网,N个节点都有可能是补偿电容器的候选安装位置,因此,优化模型的控制变量就是所有负荷节点在不同负荷水平下的电容器投入容量。写成式(18)所示向量形式:
(18)
为了方便起见,在进行配电网潮流计算和配电网损耗计算时,根据投入的电容器安装容量进行计算。在对电容器的投资费用进行计算时,将安装容量转换为电容器投入组数,这样就表示成各个节点在最大、一般、最小负荷方式下投入的电容器组数:
(19)
2.3 解空间和初始解群体的改进
配电网无功补偿配置的最优解,通常只需选取一部分节点进行补偿。在大规模的配电系统中,补偿节点数更是远小于负荷节点数[6]。
初始化时,根据配电网的具体情况设定补偿节点数的最大可能值NCmax。 NCmax是1~N的随机整数,作为电容器的候选补偿节点数,其余的N-NCmax个节点作为非候选补偿节点,这N-NCmax个节点在解中的所有相应元素值均为0。 对于任一候选补偿节点j,随机生成3个0~Vmax的数值(Vmax为PSO算法中的最大速度),作为在各个负荷水平下该节点投入的补偿容量。
照此设置,可以在很大程度上避免优化算法迭代过程中因搜索冗余空间而大量耗费时间的缺陷,有效地提高了算法的优化效率和搜索精度。
2.4 适应度函数的设置
对于配电网有功网损F1,当状态变量各节点的电压有效值和电压总谐波畸变率值不满足约束条件时,需要引入适当惩罚函数处理状态变量越限,即在目标函数中引入惩罚函数的方法计算有功网损。引入惩罚函数后配电网有功网损的适应度函数为
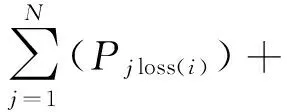
(20)
式中,γVU、γVL和γTHD分别为电压上限约束、电压下限约束及THD上限约束的惩罚因子。
3 算例及应用分析
为了验证优化模型和求解方法的有效性和实用性,选取IEEE11节点配电网和实际配电网进行优化计算分析。
3.1 IEEE11节点配电网
IEEE11节点配电网的数据中[7],出线首端根节点的电压为恒定值10.5 kV,假设该系统的末端节点8含有60%的非线性负荷,它主要向系统注入5、7、9、11次谐波。节点电压的上限、下限值分别为9.7、11.0 kV,电压总谐波畸变率的上限值为4%。
PSO算法的运行参数设置如下:种群大小N=50;维数为33;惯性权重ωstart=0.9;ωend=0.4;加速因子c1start=1,c1end=1.5;c2start=2;c2end=1.5;电容器的单位容量Qs=5 kVar;固定电容器单价Kc1=1 500元;可投切电容器单价Kc2=3 000元;最大迭代次数为50次。图1所示为IEEE11节点配电网拓扑图。

图1 IEEE11节点配电网拓扑图
根据表1所示无功补偿配置方案进行优化,由表2知,配电网经过无功补偿配置优化各负荷水平下的有功网损均有所下降,降幅分别为11.82%、9.97%、8.92%。由图2、图3可知,优化后配电网各节点的电压水平和电压总谐波畸变率均有所改善。

表1 IEEE11节点配电网的无功补偿配置方案
注:F表示固定电容器;S表示可投切电容器。

表2 IEEE11节点配电网的优化计算结果
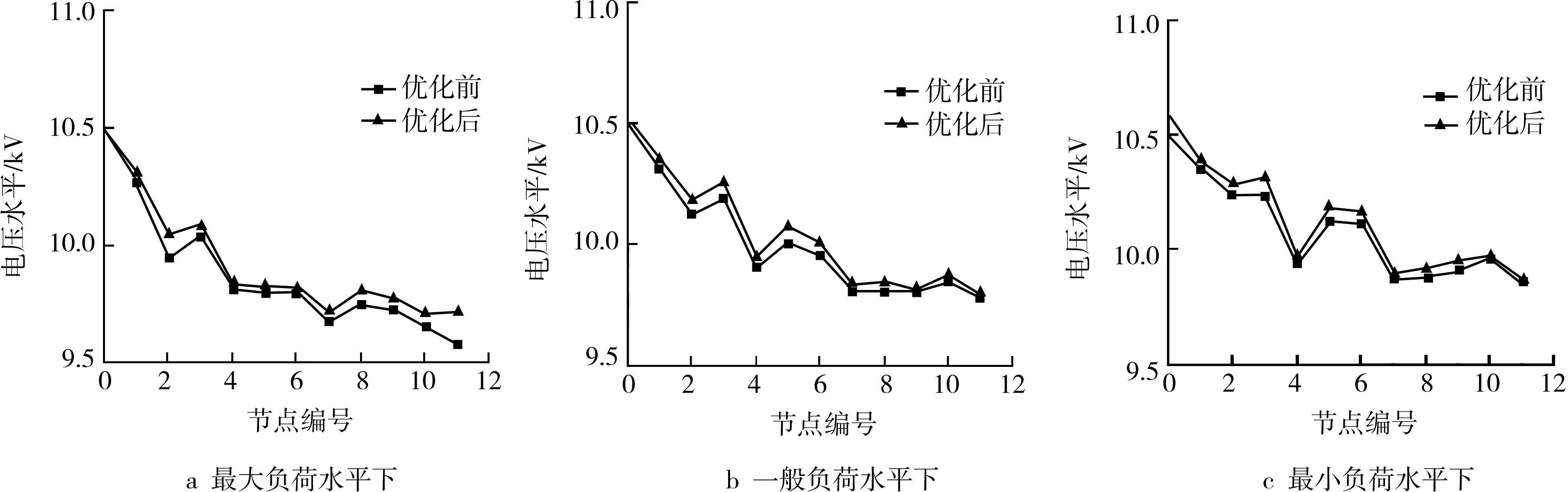
图2 优化前后各负荷水平下各节点电压有效值

图3 优化前后各负荷水平下各节点THD值
3.2 实际配电网应用
采集整理供电公司的30台变压器数据:5、6、15、30号变压器在最大负荷方式下的电压水平分别为9.419、9.406、9.426、9.424 kV,电压水平过低;THD值分别为5.367 1%、4.895 6%、4.743 7%、4.318 7%,均超过了国标规定的4%。
采用基于改进PSO算法的配电网无功补偿配置优化模型和求解方法进行无功补偿配置优化计算,限定该系统中最多有10个补偿节点。基于PSO算法的运行参数设置如下:种群大小N=50;维数为90;惯性权重ωstart=0.9,ωend=0.4;加速因子c1start=1,c1end=1.5,c2start=2,c2end=1.5;电容器单位容量Qs=10 kVar;固定电容器单价Kc1=3 000元,可投切电容器单价Kc2=6 000元;最大迭代次数为300次。表3所示为实际配电网无功补偿配置方案。图4所示为优化前后各变压器的电压有效值。图5所示为优化前后各变压器的THD值。
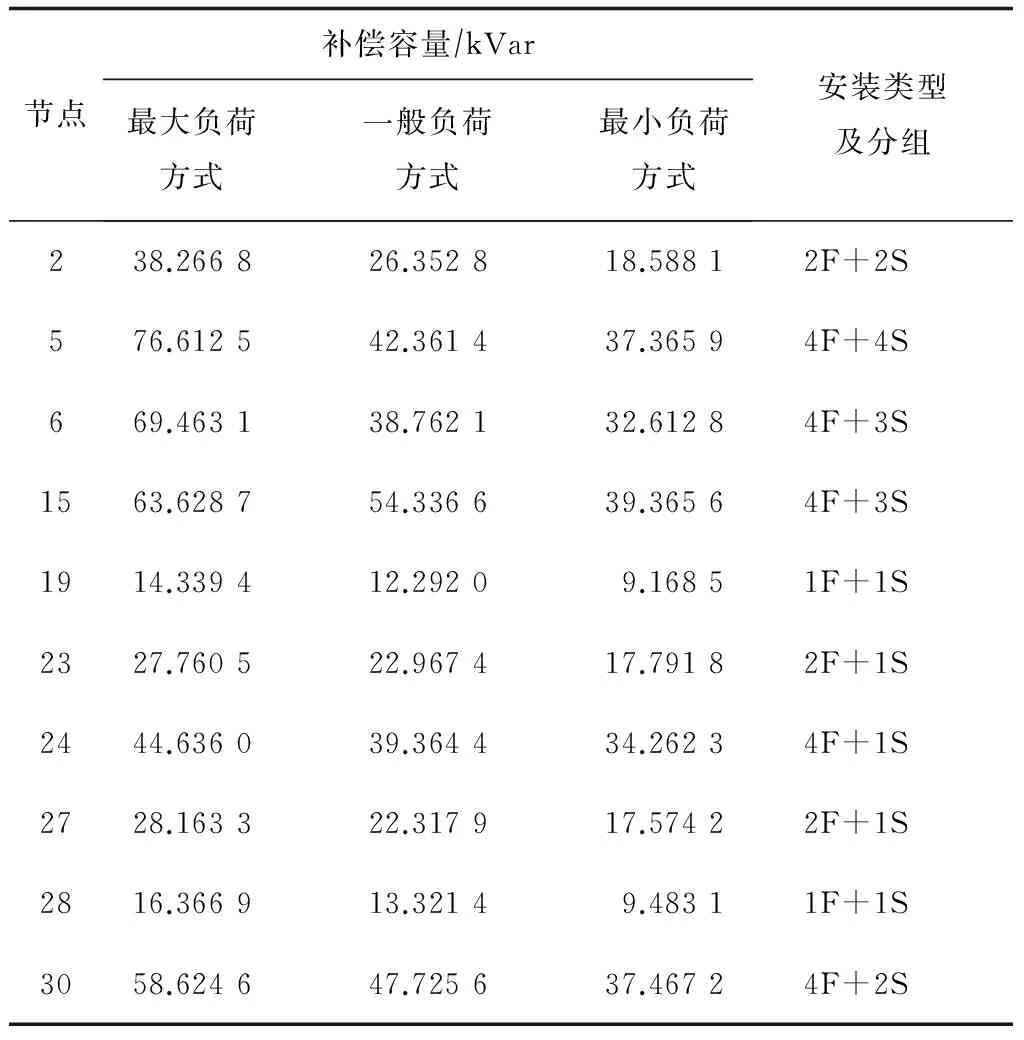
表3 实际配电网无功补偿配置方案
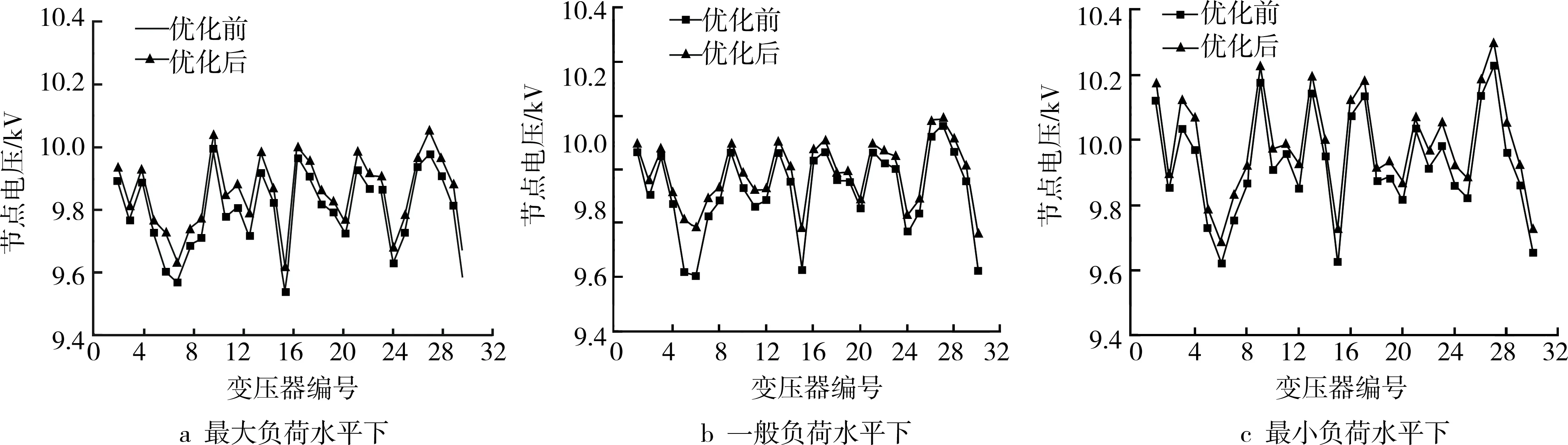
图4 优化前后各变压器的电压有效值
经过优化计算,配电网的最大负荷水平、一般负荷水平、最小负荷水平下有功网损分别为522.749 3、459.631 3、402.833 5 kW,优化前分别为584.407 3、504.327 7、426.237 5 kW,电容器的投资费用为19.8万元。因此,采用优化配置方案使配电网的有功网损分别减小了61.658、44.696 4、23.404 kW。优化后,5、6、15、30号变压器在最大负荷方式下的电压水平为9.619、9.586、9.626、9.574 kV,电压总谐波畸变率为3.884 1%、3.754 2%、3.632 5%和3.761 5%,经过补偿后电压水平和电压总谐波畸变率均为合格。其他变压器的电压水平和电压总谐波畸变率均得到了不同程度的改善。
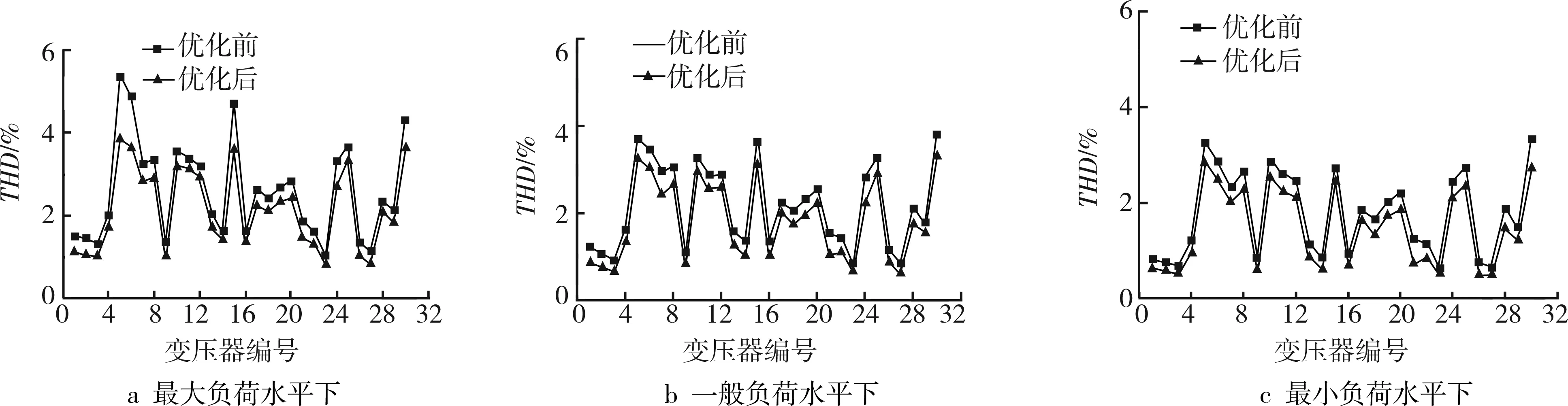
图5 优化前后各变压器的THD值
4 结 语
本次研究针对存在谐波畸变情况的配电网无功补偿配置优化问题,根据实际情况建立了考虑谐波因素的配电网无功补偿配置优化模型,在该模型的基础上提出了改进PSO算法的求解方法。
针对标准粒子群优化算法的收敛性能缺陷,对其惯性权重和加速因子的设置进行了改进,进一步改善了算法的收敛性能。
选取IEEE11节点配电网和实际配电网进行无功补偿配置优化计算,该模型和方法能够有效地改善电压水平、抑制谐波并降低配电网有功网损。
[1] 靳龙章,丁毓山.电网无功补偿实用技术[M].北京:中国水利水电出版社,2007:30-35.
[2] RAMA I S,RAMACHANDRAN K,HARIHARAN S.Optimal Reactive Power Allocation for Improved System Performance [J].IEEE Transactions on Power Apparatus and Systems,1984,PAS-103(6):65-66.
[3] BAGHZOUZ Y,ERTEM S.Shunt Capacitor Sizing for Radial Distribution Feeders With Distorted Substation Voltage[J].IEEE Transactions on Power Delivery,1990,5(2):650-657.
[4] SHI Y,EBERHART R C.Fuzzy Adaptive Particle Swarm Optimization[C]∥Proceedings of the Congress on Evolutionary Computation.Seoul,Korea,2001:101-106.
[5] 纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009:16-17.
[6] 孙白艳.计及谐波影响的配电网电容器优化配置研究[D].绵阳:西南科技大学,2016:6.
[7] BARAN M E,WU F F.Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing[J].IEEE Transactions on Power Delivery,1989,4(2):1401-1407.
Optimization Method of Reactive Power Compensation Configuration Considering Harmonic Factor in Distribution Network
CHENXiaochun1WANGYaofei1SONGYafu1WANGLina1LIUYang1ZHANGZhanlong2DANYihua2
(1. Jinyun Power Supply Company, Jinyun Zhejiang 321400, China;2. State Key Laboratory of Power Transmission Equipment and System Security and New Technology,Chongqing University, Chongqing 400044, China)
As reactive power compensation configuration optimization is seriously affected by harmonic pollu-tion in distribution network, this paper aims to build a simplified reactive power compensation configuration optimization model considering harmonic factor. First, we restrict and control the effective value of the voltage and the total harmonic distortion rate of the voltage of each node within the allowable range, and select the minimum objective function. Then we improve the algorithm in view of the local optimal convergence problem when conducting particle swarm optimization for reactive power compensation. The improved algorithm is applied to the simplified reactive power compensation configuration optimization model. Finally, this model is used in IEEE11 node distribution network for actual distribution optimization and calculation. The results show this method can improve the voltage level, restrain harmonics and reduce the active power loss of distribution network effectively.
harmonic; distribution network; reactive compensation; particle swarm algorithm
2016-09-20
中央高校基本科研业务费项目“电力电缆接头状态非接触式检测原理及方法研究”(CDJXY150008)
陈晓春(1970 — ),男,浙江缙云人,高级工程师,研究方向为电力系统及其自动化。
TM154
A
1673-1980(2016)06-0127-06

