基于Arnold变换与CNN系统的彩色图像加密算法
朱 艳 平
(信阳农林学院信息工程学院, 河南 信阳 464000)
基于Arnold变换与CNN系统的彩色图像加密算法
朱 艳 平
(信阳农林学院信息工程学院, 河南 信阳 464000)
为了提高图像信息的安全性,提出基于Arnold变换策略和细胞神经网络的彩色图像加密算法。首先对高度和宽度不同的图像进行处理;再对处理后图像的3个颜色分量分别进行Arnold置乱,置乱的迭代次数由明文图像、加密密钥和变换周期所决定;最后对置乱后的图像进行加密处理。解密时需根据变换周期决定Arnold反置乱的方法。从加密效果、密钥敏感性、密钥空间等方面,对该加密算法进行仿真研究,通过实验验证了该算法较强的安生性和鲁棒性。
Arnold变换; 细胞神经网络; 图像加密; 安全性; 鲁棒性
随着网络技术的迅猛发展,图像作为人们交流和信息分享的载体,应用范围已扩展到各个领域,其安全性也日益受到重视[1]。传统的加密方法已不能满足图像通信的实时性要求,使用混沌技术进行加密逐渐成为研究的热点方向[2]。
Arnold变换是一种非线性映射,是二维矩阵位置置乱的常用策略之一[3]。细胞神经网络(Cellular Neural Network,缩写为CNN) 是一种大规模非线性计算机仿真系统,混沌动力学特性复杂,可实现高速并行计算,便于实现大规模集成电路,故适合将其应用于图像加密系统中[4]。
本次研究中,采用Arnold变换和6维CNN超混沌系统对图像进行加密。Arnold变换只能针对高度和宽度相同的图像进行置乱,处理后使其具有通用性。当加密图像的高度和宽度不同时,应对其进行转换,使图像的高度和宽度变得相同,然后对转换后的图像进行Arnold置乱和CNN混沌加密处理。Arnold置乱的迭代次数由明文图像、CNN加密密钥和变换周期所决定。彩色图像的红色分量、蓝色分量和绿色分量的置乱次数和加密密钥均不同,从而提高了加密系统的安全性。解密时,由置乱次数来决定Arnold变换的恢复方法,从而提高了加密系统的执行效率。
1 Arnold变换策略
对于一个N×N的2维矩阵,Arnold变换如式(1)所示[5-6]:
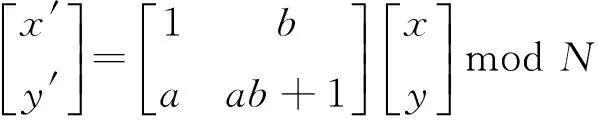
(1)
式中:[x,y]T为变换前的位置值;[x′,y′]T为变换后的位置值;a,b为模板参数,这里取值均为1。 Arnold变换具有周期性,若此矩阵进行Arnold变换的周期为P,置乱迭代次数为R,则经过P-(R mod P)次置乱,即可恢复原始矩阵。也可以进行R次逆变换恢复原始矩阵,逆变换公式如式(2)所示[7]:

(2)
2 6维CNN超混沌系统
全互连n阶细胞神经网络可用式(3)所示动力学方程表示[8]:
(3)

(4)
若初始值x1(0)的值为0.1,其他初始值的值均为0.2,则该系统产生的部分超混沌吸引子如图1所示。
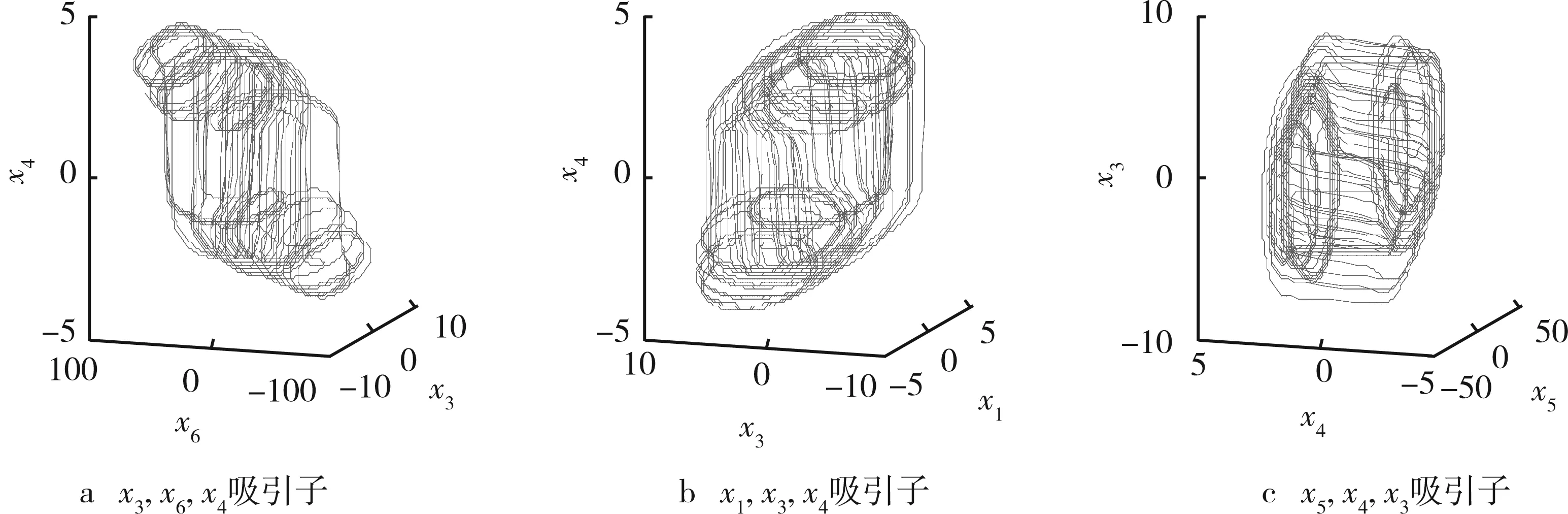
图1 6维CNN超混沌系统的部分超混沌吸引子
3 图像加密算法步骤及描述
(1)对图像进行处理。获取图像的高度M,宽度N。若M=N,则不对图像进行处理,令S=N。若M≠N,则令Q=sqrt(M×N),如果Q=fix(Q),则S=Q,否则S=fix(Q)+1。将M×N的图像按先行后列的顺序依次存入S×S的矩阵中,数据不够则用0填充,需填充S×S×3-M×N×3个数据。其中sqrt表示求算术平方根,fix表示取整。
(2)由6维CNN超混沌系统生成N×6个超混沌值。取其小数点后3位数字,对256进行取模运算,将处理后的混沌值作为密钥备用。
(3) 对图像进行Arnold置乱。彩色图像有3个颜色分量,分别对红色分量、蓝色分量和绿色分量进行置乱,各自的置乱次数由式(5)计算得出:
(5)
式中:DR、DG、DB分别为红色、蓝色和绿色分量的置乱次数;RGB(S/2,S/2,1) ,RGB(S/2,S/2,2),RGB(S/2,S/2,3)分别为明文图像第S/2行第S/2列像素的红色、蓝色和绿色分量的值;key(S/2,L2)为6维CNN超混沌系统生成的第L2路混沌序列第S/2个混沌值; L为循环次数,取1和2; P为变换周期;mod表示求余。
(4) 对置乱后的图像进行加密处理:
(6)
式中:FM(i,j,1)、FM(i,j,2)、FM(i,j,3)分别为加密后图像第i行第j列像素的红色、蓝色和绿色分量的值;CM(i,j,1)、CM(i,j,2)、CM(i,j,3)分别为经过第3步置乱后的图像第i行第j列像素红色、蓝色和绿色分量的值;key(i,L2)为加密密钥,i和j的取值从1到S,L为循环次数;⊕为异或运算。
将加密后的图像数据FM转至第3步,重复第3步和第4步,循环2次。解密过程是加密过程的逆过程。为了提高解密效率,在进行Arnold变换恢复时采用如下策略:若置乱次数R≤P/2,则通过逆变换公式(2)进行恢复,否则利用其周期性进行恢复。若M≠N,则需将解密后的图像按先行后列的顺序依次存入M×N的矩阵中,去掉填充数据,最终恢复原始图像。
4 仿真实验分析
4.1 图像加密效果仿真
以分辨率为像素200 ppi×200 ppi的Lena图和分辨率为像素768 ppi×512 ppi的Monarch图作为加密对象,采用上述加密算法对其进行加密和解密。图2所示为图像加解密效果图。
从图2可以看出,无论高度和宽度相同与否,此算法的加密效果均较佳。

图2 图像加解密效果图
4.2 性能分析
以经典的Lena图为例,对该加密算法进行性能分析。
(1) 密钥敏感性分析。当解密密钥与加密密钥完全相同时,得到正确的解密图;当解密的初始值密钥x1(0)比加密时的密钥多10-17,则得到错误的解密图。即使解密密钥与加密密钥相差很小,解密结果也会完全错误。该加密算法中其他密钥的敏感性分析与此类似,该算法具有很强的密钥敏感性。
(2) 密钥空间分析。该加密算法中的Arnold变换有2个模板参数,6维CNN超混沌系统有78个模板参数,6个初始值共有86个密钥。若计算机的计算精度为16位有效数字,则该加密算法的密钥空间为101 376。密钥空间巨大,可有效抵御穷举攻击。
(3) 统计特性分析。以红色分量为例进行直方图分析,蓝色分量和绿色分量与此类似。图3所示为图像加密系统直方图分析结果。
从图3可知,原始图像的直方图呈山峰状,颜色值的分布极不均匀;加密图像的颜色值出现的频数在150上下波动,分布较为均匀。明文图像的统计特性已经被打破,该算法可有效抵御攻击者的统计分析攻击。
(4) 相关性分析。随机抽取原始图像和加密图像相邻像素值各(S/2)×(S/2)对,分别计算各颜色分量水平方向、垂直方向和对角方向的相邻像素相关性。表1所示为图像加密系统相关性分析。

图3 图像加密系统直方图分析结果
表1中的R、G和B分别表示红色、绿色和蓝色分量。 相关性分析结果显示,明文图像相邻像素之间存在着极强的相关性,而加密后的图像相邻像素之间为极弱相关或无相关,加密系统的安全性更高。
(5) 抗噪性和抗剪裁性分析。图像加密算法应该具有良好的抗噪性和抗剪裁性。图4 所示为受噪声攻击和剪裁攻击的图像解密效果图。其中,a图为密文图像遭受均值为0、方差为0.01的高斯噪声攻击后的解密结果; b图为密文图像遭受噪声密度为0.05的椒盐噪声攻击后的解密结果;c图为密文图像遭受左上角1/4剪裁攻击后的结果;d图为遭受剪裁攻击后的解密结果。

表1 图像加密系统相关性分析

图4 受噪声攻击和剪裁攻击的图像解密效果图
可以看出,该加密算法即使受到了强烈的噪声攻击和剪裁攻击,仍能够有效地解密并显示原始图像信息,具有很强的鲁棒性。
5 结 语
本次研究提出一种基于Arnold变换和6维CNN超混沌系统的图像加密算法,并从加密效果、密钥敏感性、密钥空间、统计特性、相关性、抗噪性和抗剪裁性等方面进行了分析。该算法克服了Arnold变换只能对高度和宽度相同的图像进行置乱的缺点,具有较高的安全性和鲁棒性。
[1] ZHANG Y S,XIAO D.An Image Encryption Scheme Based on Rotation Matrix Bit-Level Permutation and Block Diffusion[J].Communications in Nonlinear Science and Numerical Simulation.2014,19(1): 74-82.
[2] 彭再平,王春华,林愿,等.一种新型的四维多翼超混沌吸引子及其在图像加密中的研究[J].物理学报,2014,63(24): 97-106.
[3] 杨洋.基于 Arnold 变换的数字图像加密算法[D].广州: 华南理工大学,2015:3-20.
[4] DAN S,HU X F,LWANG L D,et al.Hybrid Memristor/RTD Structure-Based Cellular Neural Networks With Applications in Image Processing [J].Neural Computing and Applications,2014,25 (2): 291-296.
[5] 吴成茂.离散Arnold变换改进及其在图像置乱加密中的应用[J].物理学报,2014,63(9): 83-102.
[6] 曹静,邓家先,邓海涛.一种基于Arnold变换和RSA的图像加密算法[J].电视技术,2015,39(3): 16-20.
[7] 杨凤霞.基于二维 Arnold 映射的彩色图像加密算法[J].小型微型计算机系统,2014,35(8): 1922-1925.
[8] 董虎胜,陆萍,马小虎.基于CNN 超混沌系统与扩展ZigZag 的图像加密算法[J].计算机应用与软件,2013,30(5): 132-136.
Color Image Encryption Algorithm Based on Arnold Transform and CNN
ZHUYanping
(Information Engineering College, Xinyang College of Agriculture and Forestry, Xinyang Henan 464000, China)
In order to improve the security of image information, a color image encryption algorithm based on Arnold transform and cellular neural network is proposed. First, we processed the images which have different height and width; then the three color components of processed image were transformed by Arnold mapping, and the plaintext image, encryption keys and conversion cycle determined the number of iterations. Finally, the transformed image was encrypted. In the decryption process, transformation period determined the Arnold anti scrambling method. Simulation research of the encryption algorithm was carried out to check the aspects of the effect of encryption, key sensitivity, key space, statistical characteristics, correlation, anti-noise and anti-cutting. Experimental results show that the algorithm has trustworthy security and robustness.
Arnold transform; cellular neural network; image encryption; security; robustness
2016-03-30
河南省高等学校重点科研项目“基于CNN超混沌系统的视频加密方案研究与实现”(15A520095);河南省高等学校重点科研项目“基于Hash函数的身份认证技术在电子商务交易平台的应用及改进”(16B520025)
朱艳平(1980 — ),女, 吉林省梅河口人,硕士,讲师,研究方向为细胞神经网络、混沌加密。
TP393
A
1673-1980(2016)06-0087-04

