基于果蝇优化广义回归神经网络的径流预测
林 晓 佳
(福建对外经济贸易职业技术学院信息技术系, 福州 350016)
基于果蝇优化广义回归神经网络的径流预测
林 晓 佳
(福建对外经济贸易职业技术学院信息技术系, 福州 350016)
针对水文径流的不确定性特点,提出一种新的径流预测模型。该模型在广义回归神经网络的基础上,采用了果蝇优化算法。通过该模型对四川省万源市后河径流进行了预测,结果显示改进后的模型预测精度明显提高。
果蝇优化算法; 广义回归神经网络; 径流预测
径流是一个涉及水文、气象及水力学等理论的复杂过程,包括降水、产流及汇流等阶段在内,受到地形、地貌、下垫面及人类活动等因素影响的复杂非线性系统[1]。人们针对径流预测作了大量研究,优化算法在径流预测中的应用普遍而广泛[2-5]。
本次研究采用了一种全新的优化算法 —— 果蝇优化算法(Fruit Fly Optimization Algorithm,简称为FOA算法),验证果蝇优化算法在径流预测中的参数优化特性。在多种径流预测方法当中,广义回归神经网络(GRNN)在学习速度和函数逼近能力上有较强的优势[6-7],需调整的参数较少(只有1个分布常数),可以迅速找到合适的预测网络。基于以上考虑,对GRNN的参数通过果蝇优化算法进行优化,将改进后的广义回归神经网络(FOAGRNN)模型应用于径流预测,分析该方法的径流预测参数优化预测效果及预测精度。
1 果蝇优化算法
1.1 果蝇优化算法简介
果蝇优化算法由台湾著名学者潘文超于2011年率先提出[8-9]。该算法与蚁群优化算法有相似之处,根据果蝇觅食行为来实现全局寻优,具有计算简便和结果精确等优点。果蝇本身具有非常发达的感官,其视觉与嗅觉更是优于其他物种。通过嗅觉确定食物源方向,然后通过视觉发现食物的位置,最后到达该位置。
果蝇优化算法模拟了果蝇利用嗅觉和视觉进行觅食的过程,基本步骤如下:
(1) 随机设置果蝇群体的初始位置(InitXaxis,InitYaxis)。
(2) 个体果蝇进入觅食阶段,飞行距离任取,前进方向则随机选择:
xi=xaxis+Random Value
yi=yaxis+Random Value

(4) 味道浓度判定值由味道浓度判定函数来确定,得到个体果蝇的味道浓度:Smelli=Function(Si)。
(6) 设味道浓度最高位置为新的群聚区域,并保留此时的x、y坐标:Smellbest=bestSmell。
1.2 果蝇优化算法实例
将果蝇优化算法用于实例计算,求取极大值。设函数Y=9-X2,此例正确结果为9。设置果蝇群体初始空间阈值为[0,10],觅食方向随机,距离阈值区间为[-1,1],迭代次数为100。程序运行结果逐渐逼近该函数极值的答案。图1所示为果蝇寻优轨迹。图2表示为迭代搜寻函数极值曲线。100次迭代计算过程中,计算值逐渐逼近正确结果“9”。当迭代次数达到100时,果蝇坐标为(62.836 3,93.062 3)。
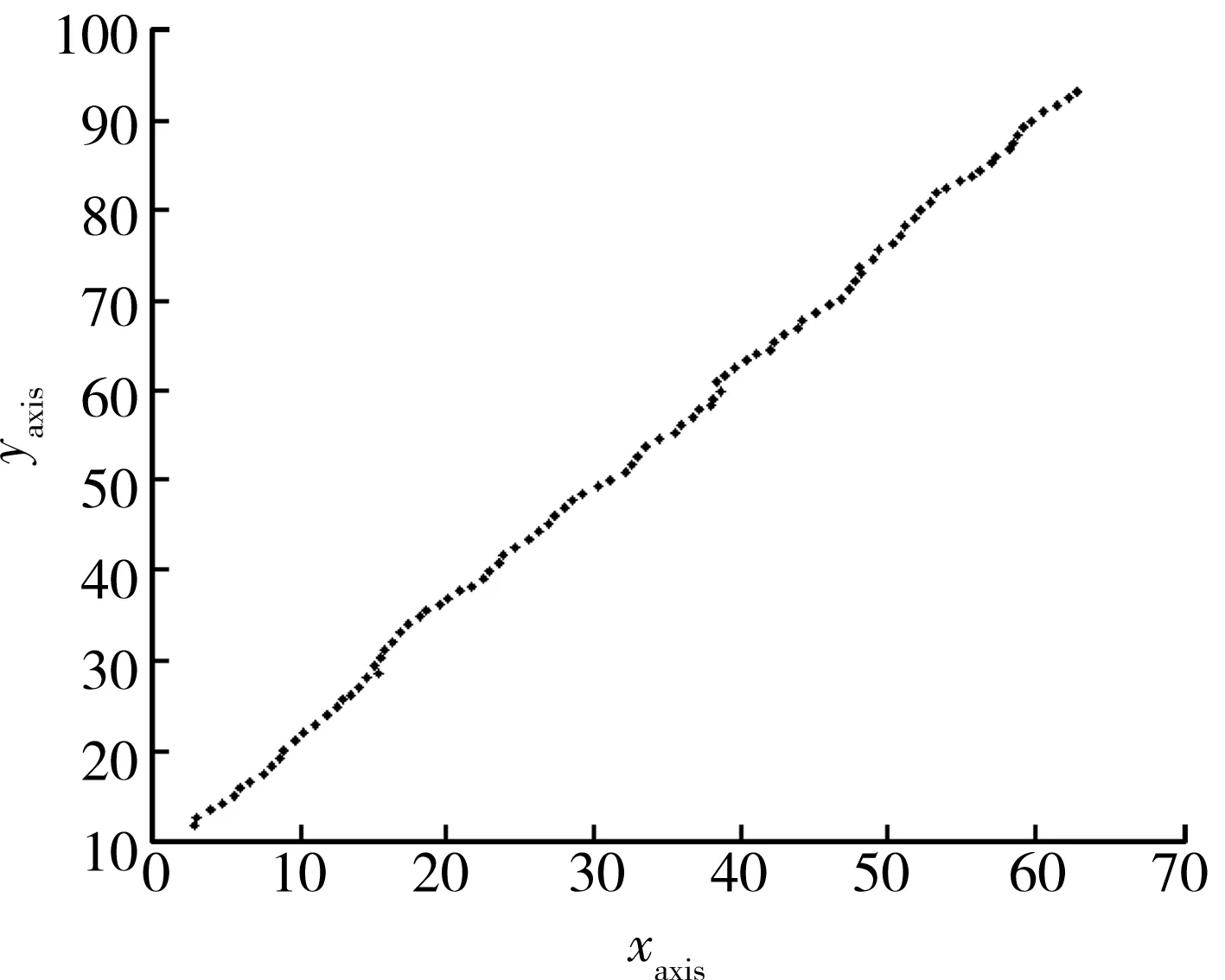
图1 果蝇寻优轨迹
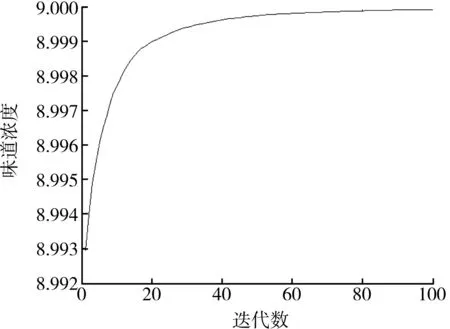
图2 迭代搜寻函数极值曲线图
2 案例分析
2.1 优化的广义回归神经网络
人为调节参数少是广义回归神经网络(缩写为GRNN)的最大特点。这样就可以将人为主观因素对预测结果的影响降到最低。广义回归神经网络在学习速度、逼近能力和分类能力等方面比其他预测方法更具明显优势[10],结果精准,计算便捷。广义回归神经网络仅涉及Spread一个参数,在运算时以机率密度函数的方式呈现而不需要假设明确的函数形式,也不用完成循环训练过程。
GRNN模型有3层结构,分别为输入层、隐含层、输出层[11-12]。FOAGRNN为FOA算法优化后的GRNN,优化步骤如下:
(1) 随机设置果蝇种群的初始位置。
(2) 确定个体果蝇与原点之间的距离,认为距离的倒数为味道浓度,计算味道浓度。味道浓度判定函数Spread作为优化对象,可用来检验将味道浓度判定值。
(3) 用输出值与目标值计算RMSE。
(4) 找出上述结果中的RMSE,作为最小值的果蝇位置。
(5) 保留最低味道浓度与坐标。
(6) 进入果蝇迭代寻优过程,在上一代最佳位置之上增加果蝇的飞行距离。
(7) 依次重复执行前面各步骤,找出使得RMSE最小值的分布参数。
2.2 FOAGENN在径流预测中的应用
所用数据来源于四川省万源市后河1959 — 2008年的年平均流量[13-14]。后河发源于万源市城北大横山,与前河、中河同为州河流域的重要河流,从大县毛坝镇开始,穿越县境西北部,与普光镇和中河交汇,流至县城交口再与前河汇合[15]。后河干流长达56 km,流域面积为3 670.7 km2,主河道平均坡降约1.1‰,流域多年平均径流量为12.47×108m3,属于山区性河流。
此次所用径流量的样本有50个,以1959 — 1993年的30个数据作为训练样本,采用GRNN和FOAGRNN的方法来测试1994 — 2008年的15个流量数据,最后将两种方法的预测结果与实测流量进行对比,来验证预测结果的可靠性及其经度。图3所示为GRNN、FOAGRNN的预测值及实测值的时间序列表。
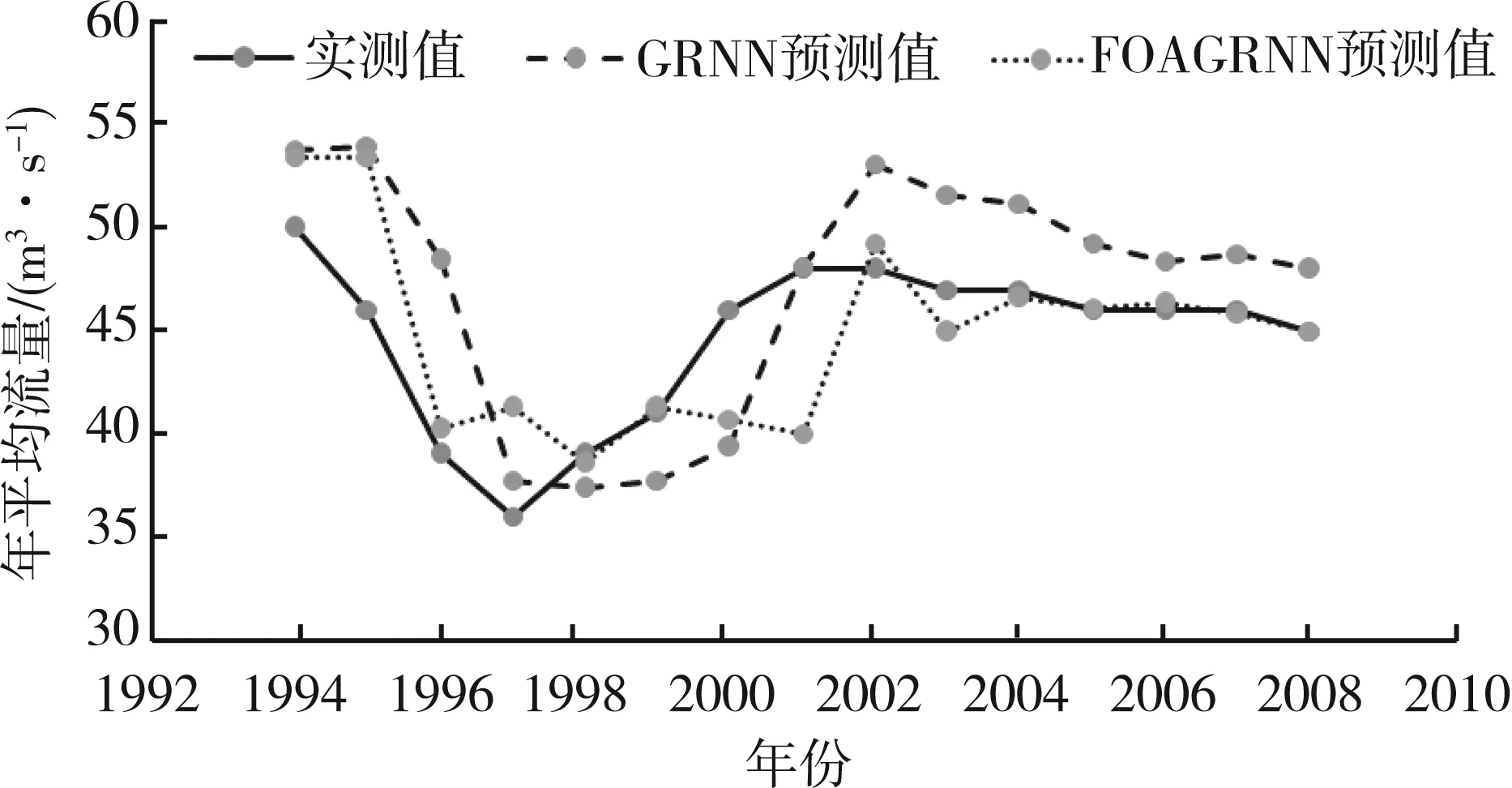
图3 GRNN、FOAGRNN预测结果及其与实测数据的比较
一般广义回归神经网络预测方法可以整体上与实测值保持一致,预测结果的精度可以满足一定的规范要求,但其预测精度仍可以进一步提升。在误差范围方面,15个预测数据中,相对误差低于10%的有7个,占预测数据总数的46.67%;相对误差10%以上的数据有8个,占全部预测数据总数的53.33%。在误差值方面,最小相对误差为0.55%,最大相对误差为17.08%,误差跨度较大。
经果蝇优化算法优化后的广义回归神经网络预测方法的预测精度提高了很多,最小相对误差为0.25,最大相对误差为14.36,缩小了误差跨度。15个预测数据中,有13个数据相对误差小于10%,占到了预测数据总数的86.67%。模型的预测误差范围得以控制,可以更好地满足预测精度的要求。
由图3可以看出,一般广义回归神经网络预测方法的预测结果整体走势与实测值基本一致。这表明GRNN在预测方面相对可靠,但其精度相对不是很好,比如2002年以后的预测数据相对误差比较大。GRNN经果蝇优化算法优化参数后再进行径流预测,预测结果的精度大幅提高,不仅保持了GRNN的优势,还能在保证GRNN本身特点的前提下提升其在预测方面的能力。
3 结 语
与传统径流预测方式不同,运用果蝇优化算法对广义回归神经网络进行参数优化,并与一般广义回归神经网络的预测结果进行了对比。一般广义回归神经网络的预测一般,虽然可以对径流做出预测,但其预测精度仍有提升空间。广义回归神经网络的参数Spread经果蝇优化算法优化后,标准误差明显降低。经由果蝇优化算法调整过的广义回归神经网络预测力和稳定性明显高于一般果蝇回归神经网络。相较于遗传算法和粒子群算法等优化算法,果蝇优化算法简单易懂,不需要过于冗长的程序代码,应用起来比较方便。作为一种优化算法,果蝇优化算法的局限性在于它只能对参数进行优化,而不能单独预测,算法的使用范围受到一定约束。该算法必须依附于其他算法,对其他算法加以改进。
[1] 于国荣,夏自强.混沌时间序列支持向量机模型及其在径流预测中应用[J].水科学进展,2008,19(1):116-122.
[2] 吴小文,李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制,2013,38(4):17-20.
[3] 白继中,师彪,冯民权,等.基于自适应调整蚁群-RBF神经网络模型的中长期径流预测[J].自然资源学报,2011,26(6):1065-1074.
[4] GUPTA Y P, GUPTA M C, KUMAR A .et al.A Genetic Algorithm-Based Approach to Cell Composition And Layout Design Problems [J].International Journal of Production Research, 1996, 34(2):447-482.
[5] Yan, S Y, Lee W T,Shih Y L.A Path-Based Analogous Particle Swarm Optimization Algorithm for Mini-Mum Cost Network Flow Problems With Concave Arc Costs [J].Transportation Planning Journal, 2007, 36(3):393-424.
[6] 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报(社会科学版),2011,29(4):1-5.
[7] 田源,张彼德,刘代伟,等.基于果蝇优化算法的GRNN水电机组状态趋势预测[J].水电能源科学,2012(12):127-129.
[8] PAN W T.A New Evolutionary Computation Approach:Fruit Fly Optimization Algorithm[C]∥2011 Conference of Digital Technology and Innovation Management Tai-Pei. 2011:1-5.
[9] Pan W T.A New Fruit Fly Optimization Algorithm:Taking the Financial Distress Model as an Example [J].Knowledge-Based Systems,2012(26):69-74.
[10] 史东亚,陆键,陆林军.基于RFID技术和FOA-GRNN理论的高速公路道路关闭交通事件对车辆影响的判断模型[J].武汉理工大学学报,2012,34(3):63-68.
[11] SPECHT D F.Probabilistic Neural Networks and the Polynomial Adaline as Complementary Techniques for Classification [J] .IEEE Trans.On Neural Networks, 1990, 1(1):111-121.
[12] SPECHT D F.A General Regression Neural Network [J].IEEE Transactions Neural Networks, 1991, 2(6):568-576.
[13] 李保琦,周泽江,马妍博.基于小波神经与随机分析的径流预测[J].西北农林科技大学学报(自然科学版),2014,42(11):169-174.
[14] 李保琦,袁鹏,马妍博.基于极大熵谱估计的径流周期分析[J].西南民族大学学报(自然科学版),2014,40(1):120-123.
[15] 马妍博,袁鹏,李保琦.前河流域上游径流的时间变化特征及变化趋势分析[J].水电能源科学,2013,31(9):16-19.
Runoff Prediction Based on Fruit Fly Optimization Algorithm Optimized GRNN
LINXiaojia
(Departmeof Information Technology, Fujian International Business and Economic College, Fuzhou 350016, China)
According to the uncertainty characteristics of hydrological runoff, a new optimization method of parameters is proposed. Based on GRNN, this method adopts FOA algorithm. Then the so-called FOAGRNN was applied in the runoff of Hou River located in Sichuan province and the results show that the improved model of FOAGRNN has a higher precision.
fruit fly optimization algorithm (FOA); GRNN; runoff prediction
2016-05-10
福建省教育厅2015年中青年教师科技项目“基于项目驱动法的数字电路教学平台的开发与应用”(JA15742)
林晓佳(1982 — ),女,福州市人,硕士,讲师,研究方向为计算机应用、网站架构、数据挖掘。
TP393
A
1673-1980(2016)06-0084-03

