基于小波变换和高阶特征提取的直驱风机轴承故障诊断方法

(中车株洲电机有限公司，湖南 株洲 412000)



基于小波变换和高阶特征提取的直驱风机轴承故障诊断方法

戴耀辉，苗 瑞，罗兴铭，辛 勤

(中车株洲电机有限公司，湖南 株洲 412000)

为了提高直驱风机稳定发电能力，提出一种新型电机轴承故障诊断方法。采用小波变换对轴承的滚动体、内圈和外圈振动信号进行分解，利用小波能谱熵和高阶统计量的双谱计算振动信号特征值，使用支持向量机根据特征值构造故障分类器，最后通过仿真验证所提故障诊断方法的有效性。

轴承；故障诊断；小波变换；能谱熵；高阶统计量；双谱分析；支持向量机

0 引 言

轴承作为直驱风机的一个重要机械部件，其运行状态直接影响风力发电机的出力。为了减少风机出力损失，轴承故障检测成为学者在风力发电领域的一个重点研究方向[1-3]。其中故障特征提取是故障检测的核心内容之一，国内外许多学者对此提出了很多办法：文献[4]提出基于永磁直驱风力发电机定子电流的频率和幅值作为特征值，使用改进的功率谱密度算法进行电机轴承故障诊断；文献[5]提出对轴承振动进行时频分析，得到故障特征频率，结合神经网络对故障进行分类识别；文献[6]利用经验模式分解将轴承故障信号分解成各类包络谱，然后进行特征频率提取，最后采用支持向量机进行故障识别；文献[7]利用固有时间尺度分解(intrinsic time-scale decomposition，ITD)和最小二乘支持向量机(least square support vector machine，LS-SVM)的风电机组轴承故障诊断；文献[8]使用本征时间尺度分解信号模糊熵，以此为特征值利用GG模糊聚类构造故障分类器；文献[9]采取奇异值分解技术对原始信号去噪后，对信号进行盲源分离提取原始故障信号。

所提方法首先采用小波变换对原始信号进行分解；然后利用小波能谱熵和高阶统计量中的双谱计算分解信号的信息熵与中心频率；接着以信息熵和中心频率作为特征值，使用支持向量机构造故障分类器；最后仿真验证所提方法的有效性。

1 理论背景

1.1 小波变换

小波变换(cotinuous wavelet transform，CWT)是一种能够将信号分解到不同频率段的技术。它具有良好的时频分析能力，与快速傅里叶变换(fast Fourier transform，FFT)相比能够展现信号的细节特征，从而在现代信号分析领域得到广泛应用。图1为小波分解示意图，图中：S为信号；L代表低通滤波器；H代表高通滤波器；↓2代表向下分解信号；cA和cD分别代表小波分解后的低频分解系数与高频分解系数。

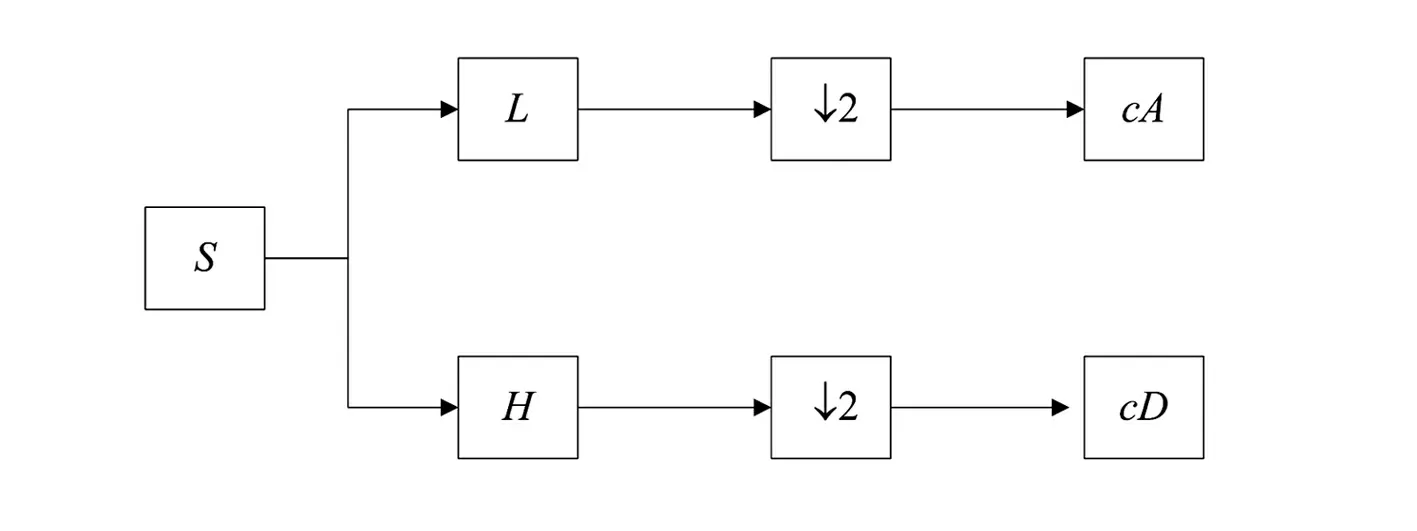
图1 小波分解示意图

连续小波变换定义为

(1)

式中：f(t)为原信号；ψ(t)为小母波；a为尺度参数；b为平移参数。小母波ψ(t)定义为

(2)

式中：a代表频率的倒数；b代表时间平移参数。离散小波变换(discretewavelettransform，DWT)是在连续小波变换(CWT)基础上发展而来，将式(2)中的a和b用2j和2k代替得到：

(3)

信号f(t)首先经过低通滤波器L和高通滤波器H得到低频小波系数cA和高频小波系数cD，接着高频小波系数继续经过滤波器L和H得到次低频小波系数与次高频小波系数，如此循环直至到指定的分解层数n。n层DWT分解可以得到n+1组离散小波系数。通过对每组系数进行信号回构就能将信号f(t)分解到不同频段下。

1.2 特征提取

轴承震动信号作为非平稳随机信号，这里采用双谱与能量熵来计算轴承故障信号的特征值。双谱是高阶累积量分析中的一种，常在现代信号处理中提取非平稳随机信号的频率、相位特征，其能自动抑制由传感器产生出的高斯噪声，被广泛应用于图像处理、模式识别等领域。

令随机变量x(t)的概率密度函数为f(x)，其第一特征函数为

(4)

从式(4)来看，第一特征函数Φ(ω)即是概率密度函数f(x)的傅里叶变换。第二特征函数ψ(ω)为

ψ(ω)=In[Φ(ω)]

(5)

高阶累积量的定义为随机变量x的k阶累积量是其第二特征函数在原地的k阶导数，即

Ck=ψ(k)(ω)|ω=0

(6)

双谱定义为三阶累积量的二维傅里叶变换，即

(7)

式中：f1、f2为频率；τ1、τ2为时间延迟常数。在式(7)中令τ1=τ2，就是信号在双谱中的对角切片，利用切片从而求得信号在去掉高斯白噪声下的频率，即双谱最大值所对应的频率。

熵在热力学中是衡量系统混乱程度一个指标，熵越高代表系统混乱程度越大。Shanno将熵的概念引入信息学科就是创建了信息熵的概念，小波变换与信息熵结合出的小波能谱熵能够度量非平稳信号在时域和频域内的复杂度。将其引入对直驱风机轴承故障信号的特征提取，能够有效提取故障的暂态信息。

设信号S经过小波分析后得到的各个频段信号的小波谱能量为E1，E2，…，Em。其中，

(8)

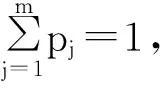
(9)

小波能谱熵能够反映轴承震动信号的空间能量信息，对各频段计算小波能谱熵可以在时频分析上精确描述轴承故障信号。

1.3 支持向量机

支持向量机(suport vector machine，SVM)是统计学习理论中的一种机器学习算法，具有很高的泛化性，在数据挖掘、回归分析和函数分类等领域被广泛应用[10]。SVM利用给定的样本构造分类超平面得到分类函数，进而对总体进行分类。

首先给定训练样本T={(x1,y1),…,(xn,yn)}，其中xi∈Rn，yi∈{1,-1}，n为样本总数，通过求解以下优化问题得到最优超平面。

(10)

式中：ω为线性权值向量；C为惩罚参数；ζi是松弛因子；yi为样本分类标签；xi为样本特征值；b是阈值。通过拉格朗日(Largrange)优化法将式(10)转化为对偶问题，如式(11)所示。

(11)

式中，ai为拉格朗日乘子。最终求得分数函数，见式(12)。

(12)

2 故障诊断方法

所提出的基于小波变换与支持向量机的轴承故障诊断方法见图2。

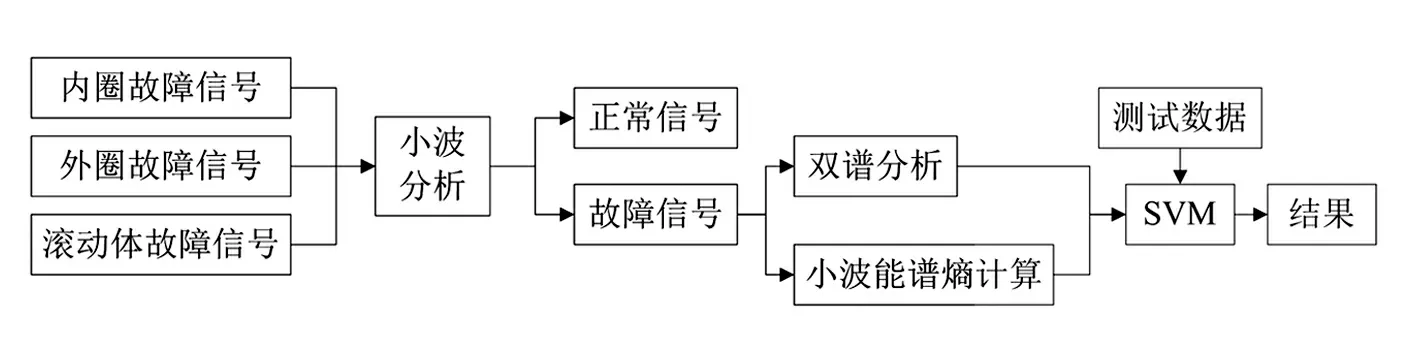
图2 轴承故障诊断方法示意图

首先对轴承的3种故障(内圈故障、外圈故障和滚动体故障)样本进行小波包分析，将故障信号与正常信号分离，同时将故障信号分解到不同频率区间内；在各频段对每种故障进行双谱分析计算故障频率，使用小波能谱熵计算各频段故障信号的空间信息量，使用计算出的故障频率和能谱熵作为每种故障信息的特征值；最后使用特征数据利用支持向量机建立故障分类超平面，同时使用测试数据对分类超平面进行验证。

3 算例仿真

采用某厂商提供的轴承震动数据，数据分为轴承测试样本、轴承滚动体故障数据、轴承内环故障数据和轴承外环故障数据。采样频率fs=12kHz，采样轴承为SKF的6205-RS深沟球轴承，轴承故障点由人工加工而成，振动信号见图3。

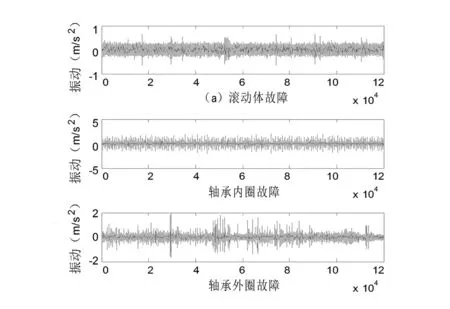
图3 轴承振动数据图

图3中滚动体故障、轴承内圈故障和轴承外圈故障数据为12万个点；对以上3类故障数据进行拆分，每类数据有6组，每组20 000个数据点。

3.1 小波分析轴承振动数据

使用小波对故障数据进行6层分解，小母波选用DB5，由于数据经过拆分，一组数据被分解成7个不同频段的低、高频信号，故每类故障总共有6×7=42个分解信号。由于篇幅所限，故只给出滚动体故障信号、内圈故障信号和外圈故障信号的第1组数据分解后的低频部分与高频故障信号部分，分别见图4、图5和图6，图中A6代表低频信号，D1代表最高频信号，D2代表次高频信号。

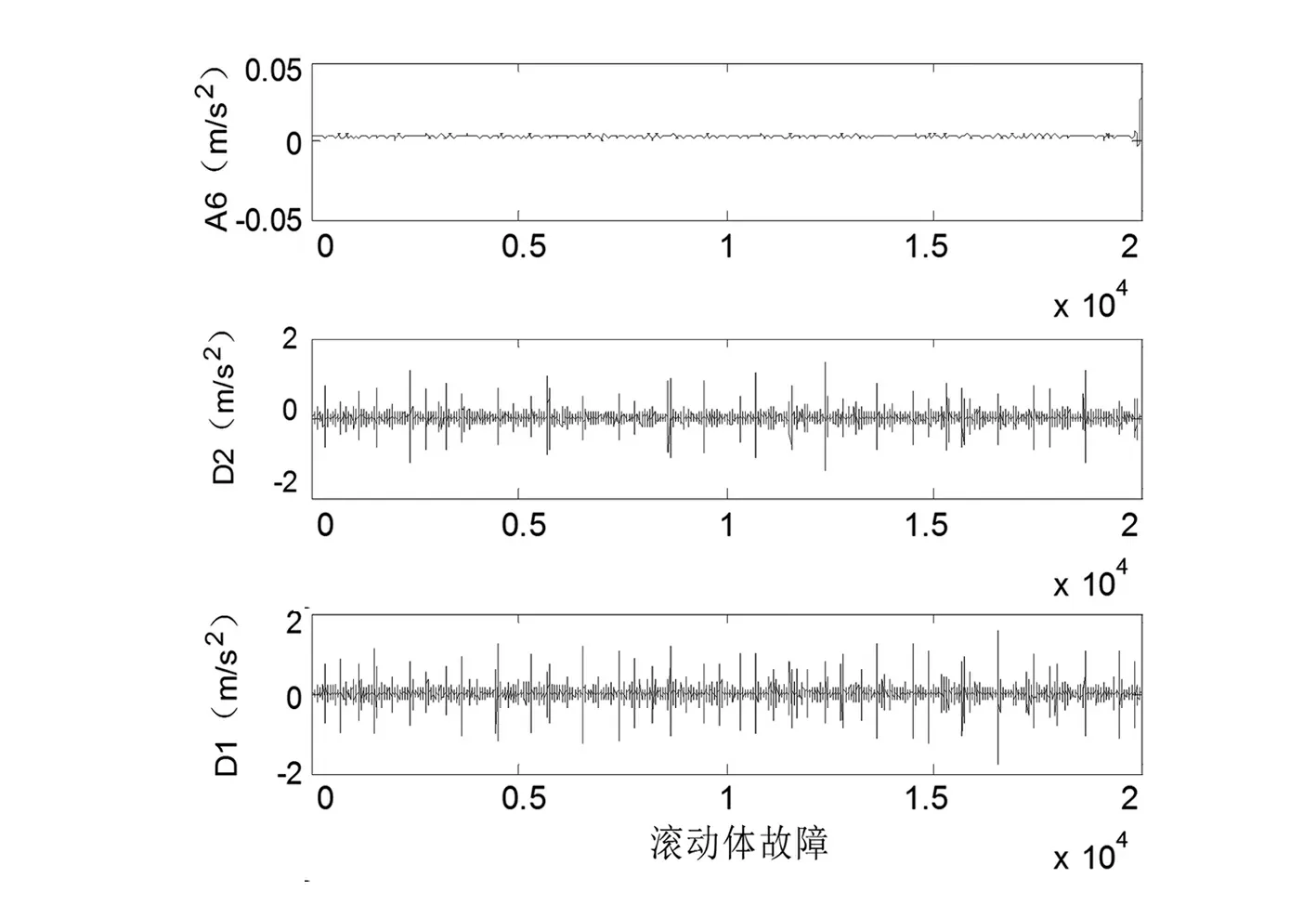
图4 滚动体故障的低频、高频小波分解信号图

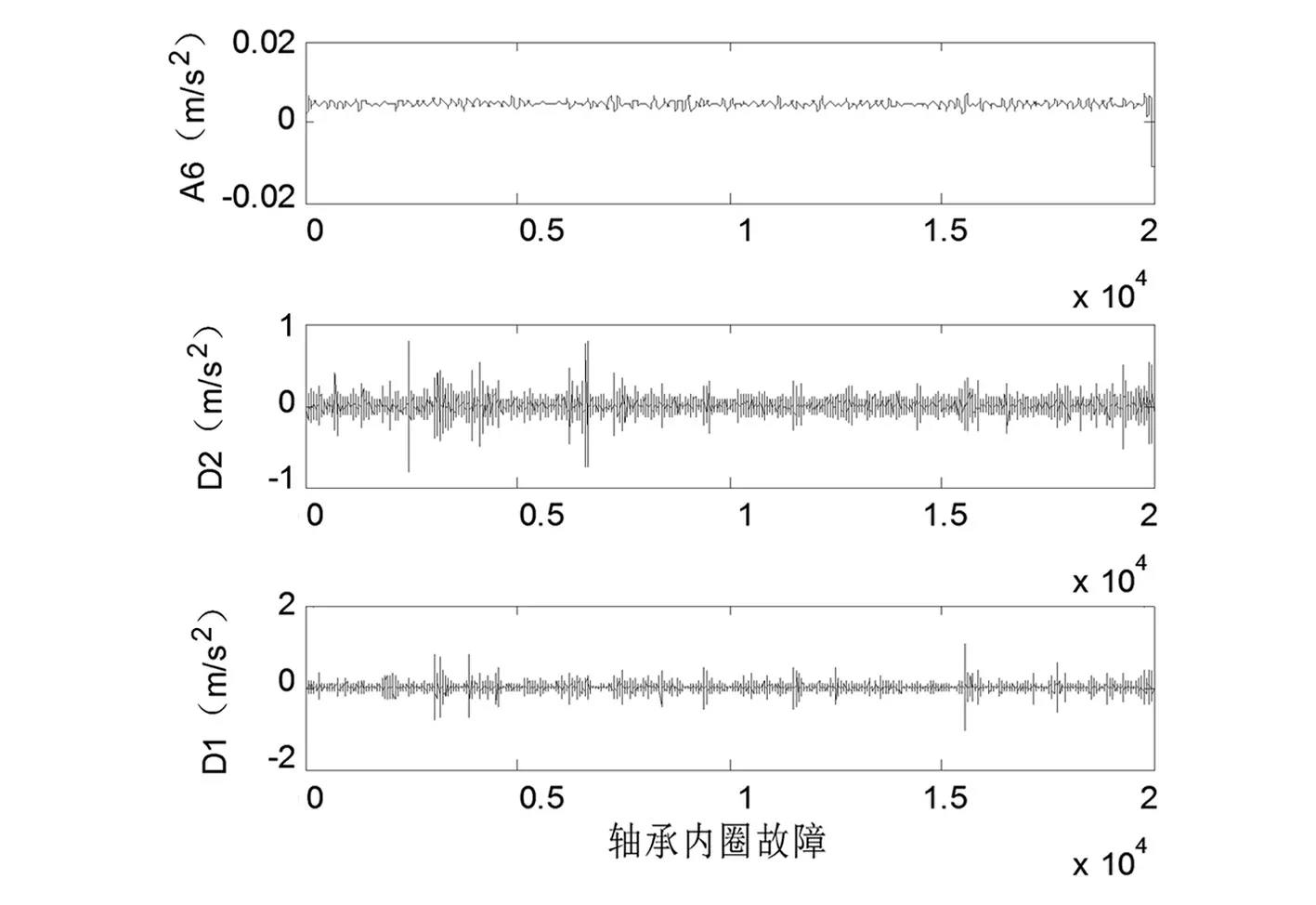
图5 轴承内圈故障的低频、高频小波分解信号图

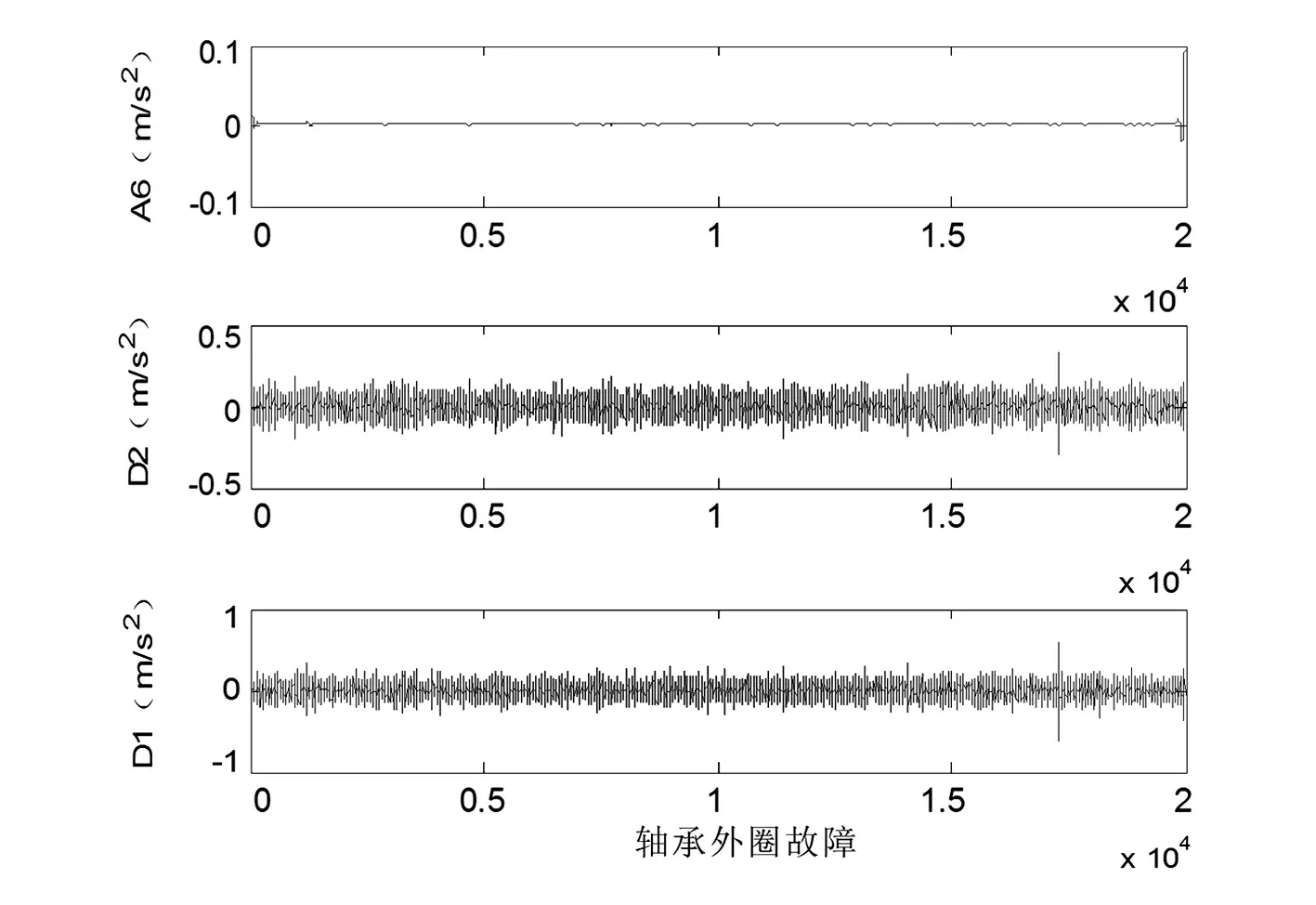
图6 轴承外圈故障的低频、高频小波分解信号图

从图4、图5和图6可以看出故障信号集中在每张图的最高频D1和次高频D2部分，其故障脉冲信号显著，幅值高于对应的低频信号A6，图4和图5中D2的脉冲信号具有明显的周期性。

3.2 计算各分解信号的小波能谱熵

根据1.2节中提出的小波能谱熵计算方法对42个分解信号进行计算，见表1。表中Ⅰ、Ⅱ、…、Ⅵ为每种故障的拆分信号，每组20 000个数据，共120 000个数据；A6、D6、D5、D4、D3、D2、D1对应3.1节中的小波分解信号，其频率段依次增加。

从表1中可以看出3类故障中小波能谱熵最大值皆在D1和D2处，滚动体故障的最大值为3.542 1(D1)，轴承内圈为3.709 5(D1)，轴承内环为3.457 2(D2)，与图4到图6中数据吻合。故此频段内一定包含故障信号，为了获得3类故障的小波能谱熵在各频段(A6至D1段)的特征值，提出了使用各频段熵的均值(Mean)作为特征值，计算结果见表2。

表2给出3种故障信号在DB5的6层分解下各频段的小波能谱熵特征值，除此之外，各频段的中心频率由所提出的双谱方法计算得到，结果见表3。

表3中NF代表归一化频率(normalizedfrequency)，3类故障在D2和D1频段中具有明显特征，即A6至D3中频率分别均匀，无中心频率，但D2和D1频段产生中心频率，即故障频率占主体。 测试信号见图7，三段测试信号从一整段信号中随机截取，每1段信号长度20000点，采样频率通过所提出的特征提取方法得到3个信号的小波能谱熵和中心频率特征值见表4。

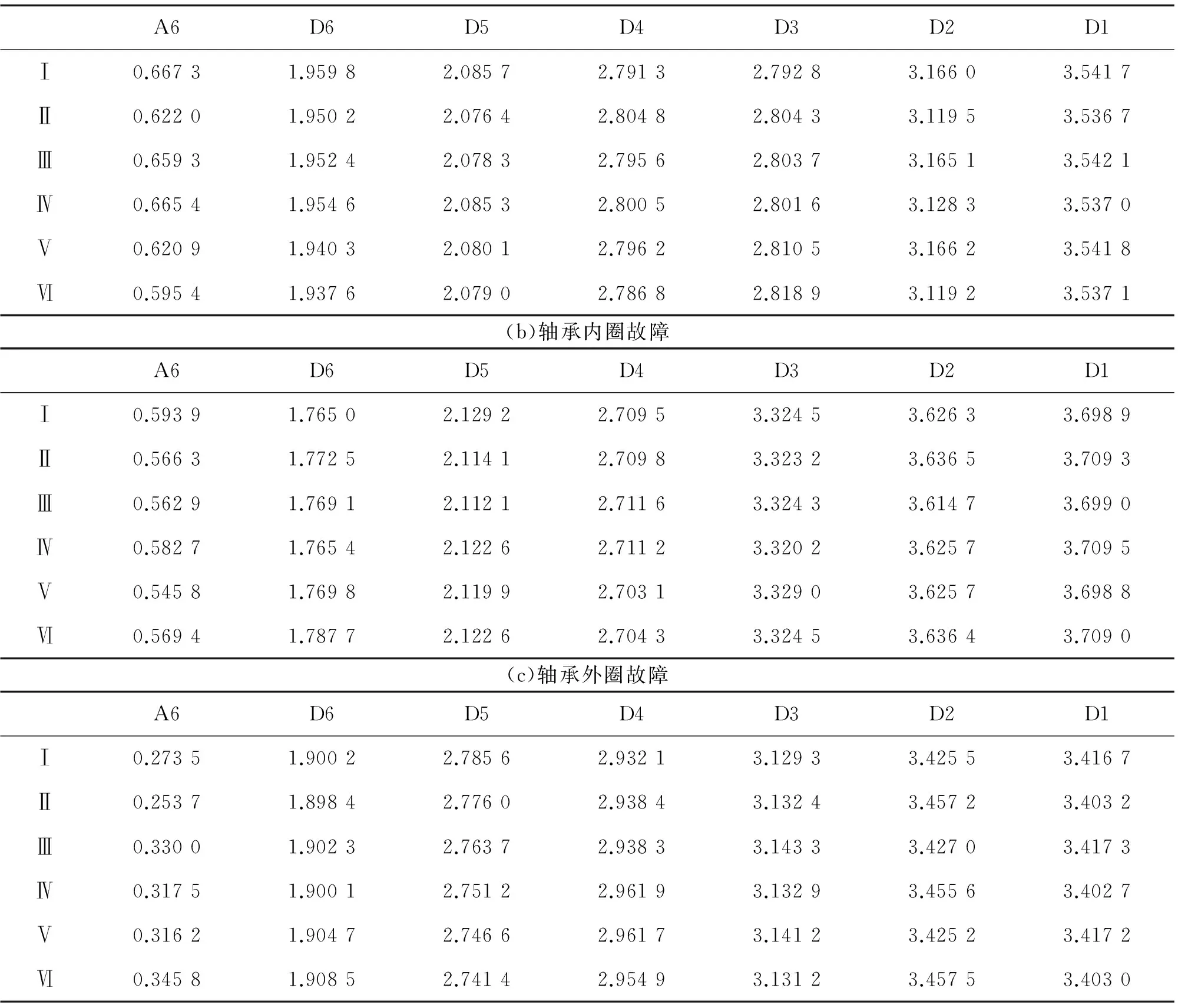
表1 3种故障信号的小波能谱熵

表2 3类故障各频段的小波能谱熵特征值(Mean)

表3 3类故障各频段的中心频率特征值(NF)

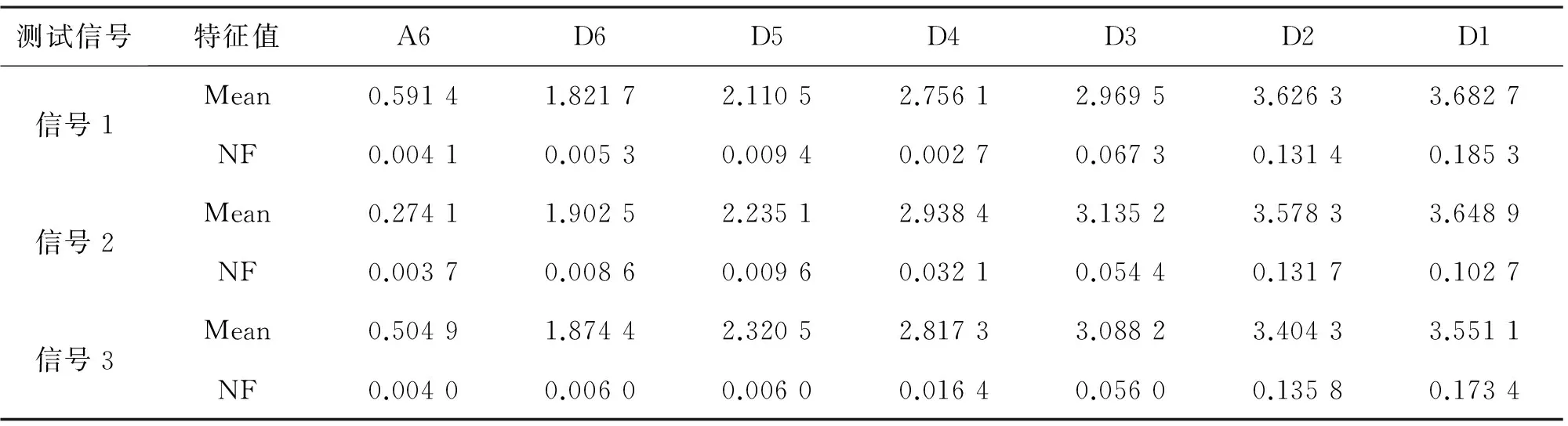
表4 测试信号的特征值

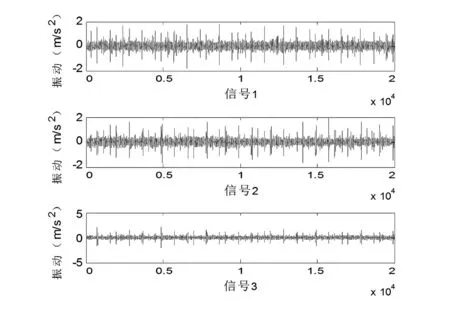
图7 测试信号

fs=12kHz。

利用支持向量机对测试信号进行分类结果如表5所示。从表5显示所提出的方法对滚动体故障、内圈故障和外圈故障的分类达到100%的正确率。

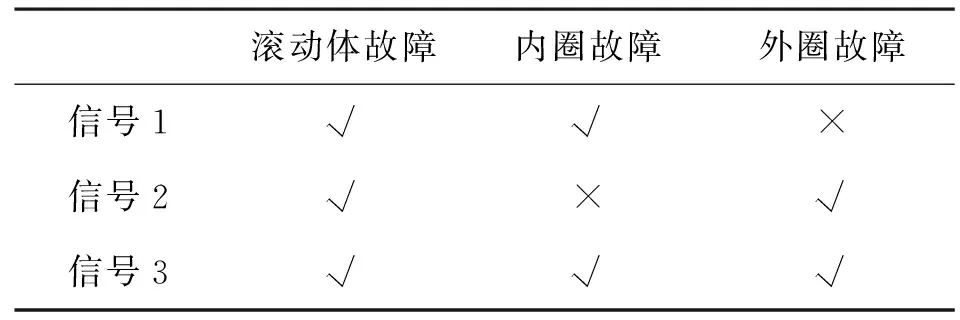
表5 测试信号故障分类结果

4 结 论

通过小波分解故障信号，使用小波能谱熵和双谱计算故障信号在不同频段的特征值，利用支持向量机使用故障特征值构建故障分类器这种方法，通过仿真验证了其有效性。

[1] 沙美妤,刘利国.基于振动信号的轴承故障诊断技术综述[J].轴承,2015,9(1):59-63.

[2] 彭富强,于德介,罗洁思,等.基于多尺度线调频基稀疏信号分解的轴承故障诊断[J].机械工程学报,2010,46(7):88-95.

[3] 张文义,于德介,陈向民.基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法[J].中国电机工程学报,2013,33(20):111-118.

[4]XiangGong,WeiQiao.BearingFaultDiagnosisforDirect-driveWindTurbinesviaCurrent-demodulatedSignals[J].IEEETransactionsonIndustrialElectronics,2013,60(8):3419-3428.

[5]BoLi,Mo-YuenChow,YodyiumTipsuwan,etal.Neural-network-basedMotorRollingBearingFaultDiagnosis[J].IEEETransactionsonindustrialElectronics,2000,47(5):1060-1069.

[6] 胡荣华,楼佩煌,唐敦兵,等.基于EMD和免疫参数自适应SVM的滚动轴承故障诊断[J].计算机集成制造系统,2013,19(2):438-447.

[7] 安学利,蒋东翔,陈杰,等.基于ITD和LS-SVM的风力发电机组轴承故障诊断[J].电力自动化设备,2011,31(9):10-13.

[8] 张立国,李盼,李梅梅,等.基于ITD模糊熵和GG聚类的滚动轴承故障诊断[J].仪器仪表学报,2014,35(11):2624-2632.

[9] 陈恩利,张玺,申永军,等.基于SVD降噪和盲信号分离的滚动轴承故障诊断[J].振动与冲击,2012,31(23):185-190.

[10] 詹仲强,陈洁,黄净,等.基于运行数据和支持向量机的风电场动态建模[J].可再生能源,2015,33(11):1640-1644.

In order to improve the stability of direct-driven wind power generation capacity, a new method of motor bearing fault diagnosis is proposed. Wavelet transform is used to decompose the vibration signal of the ball, inner raceway and outer raceway of the bearing, and the wavelet energy spectrum entropy and the bispectrum of high order statistics are used to calculate the characteristic value of vibration signal. The fault classifier based on characteristic value is constructed by support vector machine, and finally the effectiveness of the proposed fault diagnosis method is verified by the simulation.

bearing；fault diagnosis; wavelet transform; energy spectrum entropy; high order statistics; bispectrum analysis; support vector machine

TH17 <文献标志码：a class="emphasis_bold"> 文献标志码：A 文章编号：1003-6954(2016)06-0041-06文献标志码：a

1003-6954(2016)06-0041-06

A 文章编号：1003-6954(2016)06-0041-06

2016-06-22)

戴耀辉(1986)，硕士、工程师，从事动车牵引变压器技术研究。